Связанные замедляющие системы

Хотя связанные замедляющие системы (СЗС), в частности противозаходные спирали, известны давно [1], их свойства были изучены достаточно полно лишь в последние годы, а их практическое применение находится пока еще на начальном этапе. Объяснить это можно, с одной стороны, относительно узкой областью применения обычных замедляющих систем (ЗС), а с другой стороны, сложностью анализа СЗС и тем более четкого представления об их физических особенностях.

Так как ЗС использовались в вакуумной электронике для обеспечения синхронного взаимодействия с электронным потоком, то и первые конструкции СЗС были предложены для управления траекторией электронов в электронно-лучевых трубках [2]. В лампах с бегущей волной (ЛБВ) со спиральной ЗС участки с противо-заходной спиралью использовались для ввода и вывода усиливаемого сигнала. Эффект перекачки сигнала из одной спирали в другую вызван отличием фазовых скоростей синфазной и противофазной волн, возбуждаемых в СЗС.

Синфазная и противофазная волны в СЗС отличаются не только скоростями, но поперечной структурой поля. Поэтому при возбуждении на синфазной волне связанные гребенки могут использоваться для продольного взаимодействия с ЭП, а при возбуждении на противофазной волне – для поперечного взаимодействия [3].

Положительные свойства СЗС проявляются наиболее ярко при так называемом «нетрадиционном» применении, применении в технологических процессах, медицине, измерительной технике и т. д. [4]. Ниже представлены результаты краткого анализа физических особенностей СЗС и даются рекомендации по их применению.

1.    Общие определения

Замедление N определяется отношением скорости света в вакууме с к фазовой скорости замедленной волны v ф . Замедляющей системой является передающая линия, замедляющая фазовую скорость электромагнитной волны по сравнению со скоростью света в окружающей среде, т. е. в вакууме. Если исключить из рассмотрения ЗС, образованные диэлектриком, то замедление волны вызывается либо увеличени-

ем пути, проходимого волной по сравнению с расстоянием в направлении распространения, либо наличием поперечных проводников, вызывающих задержку распространения волны. В терминологии, используемой при замене реальной линии передачи эквивалентной ей длинной линией, первое вызывает увеличение погонной индуктивности, а второе – погонной емкости. Однако и в том и другом случае ЗС является линией передачи, по крайней мере один проводник которой образован периодической последовательностью связанных друг с другом проводников с токами, протекающими как в поперечном, так и в продольном направлении. Этот проводник (или проводники) называется импедансным , а другой проводник – экранным . Именно наличие импедансного проводника вызывает замедление волны.

При определении замедления можно пользоваться отношением фазовой постоянной β к волновому числу k , определяемыми выражениями:

β = ω , k = ω ε ₀ µ ₀ . (1) v ф

Здесь ω – угловая частота, ε ₀ и µ ₀ – диэлектрическая и магнитная проницаемости. Наличие замедления приводит к тому что длина волны в ЗС, т. е. длина замедленной волны λ _з в N раз меньше длины волны в свободном пространстве λ .

Периодичность ЗС определяется периодом Т расположения проводников и является важным параметром, влияющим на свойства ЗС, в частности на распределение поля замедленной волны в прилегающем к ЗС пространстве.

Благодаря замедлению волна может распространяться без излучения в окружающее пространство даже при отсутствии экранного проводника, т. е. по одному импедансному проводнику. При этом интенсивность поля уменьшается от поверхности импедансного проводника, а его поперечное распределение характеризуется т. н. поперечной постоянной τ, связанной с фазовой постоянной и волновым числом соотношением

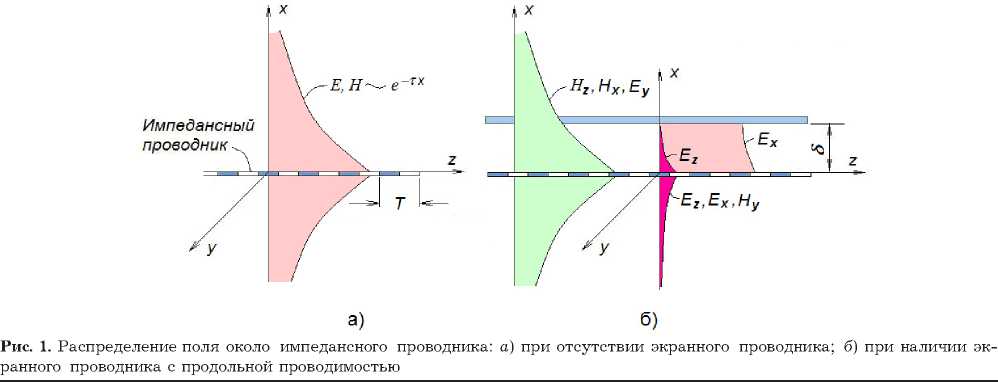
τ ² = β ² - k ². (2) В случае плоских проводников это распределение близко к экспоненциальному с показателем -τ x^ , где x^ – расстояние от поверхности проводника (рис. 1, a ). В случае цилиндрических проводников, поперечное распределение определяется модифицированными функциями Бесселя. В представляющих практический интерес случаях, когда N >  3, τ ≈ β .

Периодичность граничных условий на импедансном проводнике, характеризуемая периодом Т , приводит к отличию продольного распределения поля от гармонического, т. е. к появлению пространственных гармоник . Хотя амплитуды пространственных гармоник становятся сравнимыми с амплитудой нулевой гармоники лишь при значениях λ _з , близких к 2 Т , в таких ЗС, как меандр-линия, в которой на низких частотах направление токов в соседних проводниках практически противоположно, магнитное поле в основном представлено ± 1 пространственными гармониками.

В большинстве случаев замедленная волна является гибридной , т. е. представляет собой сумму волн электрического и магнитного типа. При этом поперечные структуры этих волн могут сильно различаться. Это особенно заметно, когда волны представлены разными пространственными гармониками, как в случае меандр-линии.

2.    Эквивалентная линия

Независимо от конфигурации проводников любая передающая линия может быть заменена эквивалентной схемой с индуктивностью в продольном и емкостью в поперечном проводниках. При относительно малой периодичности, когда каждая из волн может быть представлена только одной пространственной гармоникой, вместо эквивалентной схемы можно пользоваться эквивалентной линией с погонной индуктивностью L0 в одном из продольных проводников и поперечной погонной емкостью C0, удовлетворяющими уравнению длинной линии

β ² = ω ² L 0 C 0 . (3)

Пользуясь соотношением (2), уравненение (3) можно упростить, исключая из индуктивности L ₀ запаздывание потенциала

τ ² = ω ² LC ₀ . (4)

Здесь L – погонная индуктивность «укороченной» эквивалентной линии, определяемая магнитным полем, возбуждаемым только поперечными компонентами токов в импедансном проводнике. При этом эквивалентная емкость определяется полем волны электрического типа, а индуктивность L – полем волны магнитного типа [5]. Из определения замедления и уравнений (3), (4) следует, что

N = 1 + ^{LC 0} . (5) ε ₀ µ ₀

Рассмотрим плоский импедансный проводник шириной H с расположенным на расстоянии δ от него экранным проводником с идеальной проводимостью в продольном направлении (рис. 1, б ). Погонная емкость такого проводника с учетом емкости его открытой поверхности определяется с помощью более общего выражения, приведенного в [5]:

C = ε ₀ τ H (1 + cth τδ ). (6) При увеличении зазора δ емкость стремится к значению, которое она принимает в отсутствие экранного проводника, т. е. 2 ε ₀ τ H , а при уменьшении δ – стремится к статической емкости ε ₀ H / δ .

Благодаря отсутствию поперечной проводимости рассматриваемого экранного проводника он не оказывает никакого воздействия на Н -вол-ну, и погонная индуктивность оказывается такой же, как и при его отсутствии. Если известно значение N для одиночного проводника, то погонная индуктивность L , как это следует из (4) и (5), определяется следующим выражением:

L =µ ^{N 1}. (7)

⁰ 2 τ H

В случае радиальной спирали H = 2 π r , где r – текущий радиус. Для цилиндрической спирали H = 2 π a , где a – средний радиус спирали. При этом в выражения для эквивалентных параметров входят модифицированные функции Бесселя. Однако на относительно высоких частотах, т. е. при значениях аргументов функций Бесселя, превышающих 3, эти выражения практически совпадают с приведенными выше.

3.    Замедление волны в СЗС

Рассмотрим обобщенную модель СЗС в виде параллельно расположенных на расстоянии 2 δ друг от друга импедансных проводников шириной H с конфигурацией, представляющей зеркальные отображения друг друга (рис. 2). Это могут быть два меандра, сдвинутых друг относительно друга в продольном направлении на половину периода, штыревые гребенки с противоположным направлением штырей, радиальные спирали и т. д. В случае радиальных спиралей, продольная координата z заменяется радиусом r . Будем полагать что каждый из этих проводников в отдельности обладает одинаковыми эквивалентными параметрами L и C , определяемыми с учетом их взаимного влияния. Справа от обобщенной модели СЗС на рис. 2 показана эквивалентная линия в виде продольных проводников с погонными индуктивностями L и поперечных проводников с последовательно соединенными емкостями С .

При противофазном возбуждении СЗС потенциалы противолежащих проводников противоположны, а направления поперечных компонент токов совпадают. В результате суммарное поле Е-волны концентрируется в области между импедансными проводниками, а суммарное поле Н-волны – снаружи проводников. При этом продольная компонента электрического поля про-

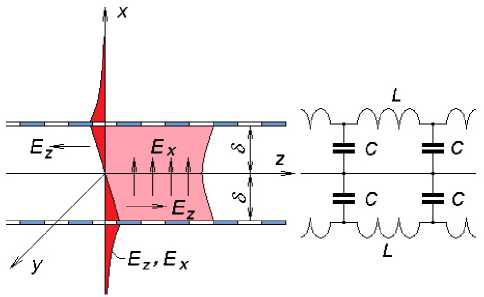
Рис. 2. Схематическое изображение СЗС и ее эквивалентная линия

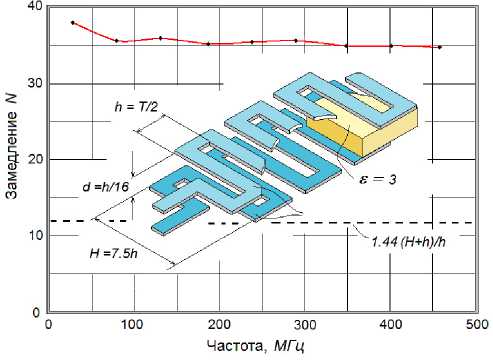
Рис. 3. Экспериментальная зависимость замедления противофазной волны в связанных меандрах от частоты; пунктиром показано геометрическое замедление с учетом влияния диэлектрика ходит через ноль на поверхности симметрии между проводниками так, как если бы эта поверхность обладала бы идеальной проводимостью в продольном направлении. Таким образом, эквивалентная емкость каждого импедансного проводника с учетом их взаимного влияния определяется формулой (6).

Напряженности магнитных полей Н-волн обоих импедансных проводников складываются снаружи проводников, и эквивалентная индуктивность каждого из них увеличивается по сравнению со значением, определяемым формулой (7). С учетом увеличения магнитного потока напишем

N - 1 -τδ

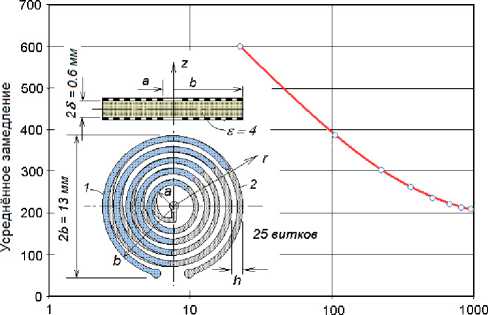
Частота, МГ ц

Рис. 4. Зависимость усредненного по радиусу спирали замедления от частоты, измеренное для связанных арифметических спиралей нально корню кубическому из волнового числа. Наличие между импедансными проводниками диэлектрика с относительной диэлектрической проницаемостью ε равносильно уменьшению зазора в ε раз и, следовательно увеличению замедления в 3 ε раз. Отметим, что многократное увеличение замедления происходит без увеличения пути, преодолеваемого электронами, т. е. без увеличения длины проводников и, следовательно, без увеличения электромагнитных потерь.

Таким образом, применение СЗС позволяет не только увеличить замедление при сохранении высокой добротности, но и управлять наклоном дисперсионной характеристики. Так, в отличие от меандра, обладающего нормальной дисперсией со значительной крутизной, дисперсия волны в связанных меандрах практически отсутствует (рис. 3). И наоборот, радиальные и цилиндрические спирали, имеющие относительно небольшую дисперсию каждая в отдельности,

C ≈

H

ε ₀ , δ

N ²

L ≈ µ ₀    .

τ H

в связке друг с другом отличаются ярко выра-(9) женной аномальной дисперсией (рис. 4).

Подставляя в формулу (5) выражения (9), находим после простейших преобразований с учетом принятых допущений

Nc ≈ 3 N , (10) kδ где замедление волны в СЗС отмечаяется индексом «с» (от английского слова coupled, т. е. связанные).

Из формулы (10) следует, что при относительно малом зазоре между импедансными проводниками замедление противофазной волны в СЗС существенно превышает замедление в одном импедансном проводнике и обратно пропорцио-

4.    Волновое сопротивление СЗС

Благодаря симметричности СЗС, а также концентрации большей части электрического поля между импедансными проводниками волновое сопротивление СЗС Z ₀ можно с достаточной точностью определить как корень квадратный из отношения L / C . Последовательное соединение импедансных проводников увеличивает волновое сопротивление СЗС вдвое по сравнению с сопротивлением каждого из них с учетом взаимного влияния:

Z 0 = 2 ^β _{τ C} ^L .                                   (11)

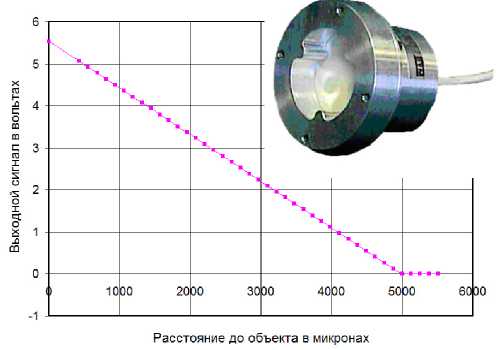
Рис. 5. Прецезионный датчик измерения зазора до металлической поверхности; линейность полученной характеристики достигается с помощью микропроцессора, преобразующего

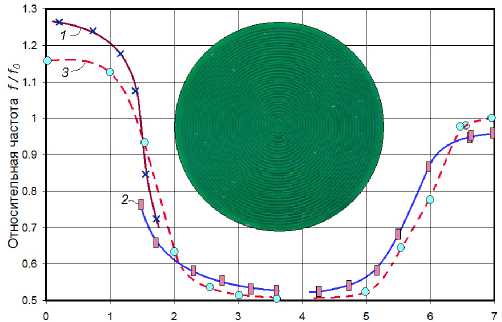
Поверхностное сопротивление в омах

Рис. 6. ЧЭ на связанных спиралях и зависимости относительной частоты измерительного генератора с ЧЭ в цепи обратной связи: 1 — тонкий слой золота на диэлектрике;

2 — имплантированный силикон; 3 — расчет

частоту генератора в напряжение

Подставляя в (11) выражения для L и C , полученные в приближении N_c >>  1, т5 <<  1, находим 2 0 . 2^ H N c .                      (12)

Из формулы (12) следует, что волновое сопротивление СЗС уменьшается с уменьшением зазора 5 , но благодаря одновременному увеличению замедления остается достаточно большим, что свидетельствует о высокой добротности элементов на СЗС.

5.    Практическое применение

Как уже отмечалось выше, при противофазном возбуждении СЗС поле Е-волны сосредоточено в основном между проводниками, а поле Н-волны - снаружи. При этом энергия электрического поля в Е-волне приблизитедьно в N ² раз превышает энергию магнитного поля, и, наоборот, энергия магнитного поля в Н-волне во столько же раз превышает энергию электрического поля, а само замедление может в десятки раз превышать замедление одного импедансного проводника. Большое замедление сопровождается большой концентрацией энергии поля как в продольном, так и в поперечном направлениях, а также пропорциональным величине замедления уменьшением длины резонансных отрезков на СЗС, т. е. возможностью концентрировать энергию электромагнитной волны в области с размерами, в десятки и сотни раз меньшими длины волны в свободном пространстве.

Наиболее очевидным, но далеко не самым важным является применение СЗС в качестве линии задержки (ЛЗ). По сравнению с ЛЗ на цилиндрических спиралях и меандр-линиях, поме- щенных в материал с большой диэлектрической проницаемостью, связанные спирали и меандры позволяют получить на порядок большее замедление без применения дорогостоящих материалов и при существенно меньших потерях [6].

Другим очевидным применением, вытекающим из возможности получения большого замедления, является микроминиатюризация пассивных элементов и функциональных устройств с распределенными параметрами, таких как резонаторы, согласующие устройства, аплитудно-частотные корректоры и др.

Почти полное разделение электрического и магнитного поля в СЗС позволяет многократно повысить чувствительность измерений параметров диэлектрических, проводящих и полупроводящих материалов [7], а также зазоров, линейных и угловых перемещений [8]. Контроль коррозии и трещин трубопроводов без удаления изоляции является одной из важнейших областей применения СЗС [9].

На рис. 5 показана характеристика датчика зазора до металлической поверхности, а на рис. 6 – характеристика датчика поверхностной проводимости с чувствительными элементами (ЧЭ) на арифметических спиралях, выполненных в виде металлизации на обеих поверхностях диэлектрической подложки. Близкий по конфигурации ЧЭ использовался при разработке датчика коррозии. Участок кривой на рис. 6, соответствующий большим значениям поверхностного сопротивления, получен в режиме синфазного возбуждения, т. е. при зондировании образцов электрическим полем ЧЭ.

Концентрация энергии электрического поля в зазоре между импедансными проводниками и возможность использования энергии ВЧ-диа-пазона позволяют намного увеличить эффективность термообработки, в частности сушки, тонких материалов, таких как ткани, бумага, фанера и прочие [10]. Размораживание пищевых продуктов, предпосевная обработка семян и клубней и т. д. – далеко не полный перечень возможных применений СЗС в сельском хозяйстве и пищевой промышленности [11]. ВЧ-нагрев т. н. высокотемпературной плазмы с одновременным контролем ее проводимости легко осуществим с помощью электродов на СЗС. Н-волна глубоко проникает в плазму, несмотря на ее высокую проводимость.

Энергия магнитного поля СЗС может быть использована в медицине для т. н. магнитотерапии. Благодаря почти полному отсутствию электрического поля и возбуждаемых им токов в теле пациента глубина проникновения поля в тело определяется только размерами электрода и длиной замедленной волны, т. е. практически отсутствует скин-эффект [12]. Другим положительным фактором является отсутствие ожога жировых тканей, вызываемого электрическим полем при использовании обычных индуктивных электродов. Искуственное ухо с устройством передачи сигнала через кожу [13], а также устройство для подзарядки батареи кардиостимулятора являются лишь некоторыми примерами возможного применения СЗС в медицине.

Исследование выполнено при поддержке Министерства образования и науки Российской Федерации,соглашение № 14.B37.21.0909 «Исследование физических процессов в мощных многолучевых СВЧ электровакуумных приборах с электродинамическими системами , выполненными на основе многомодовых резонаторов».