Свойства одной конечно-аддитивной меры на lp, инвариантной относительно сдвигов
Автор: Бусовиков В.М.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Математика
Статья в выпуске: 2 (38) т.10, 2018 года.
Бесплатный доступ
Изучаются свойства конечно-аддитивной меры на семействе банаховых пространств последовательностей ��, инвариантных относительно сдвига, предложенной В. Ж. Сакбаевым в [1]. В частности, устанавливается её �-конечность для 1
Конечно-аддитивная мера, трансляционно-инвариантные меры на банаховых пространствах, верхняя и нижняя меры
Короткий адрес: https://sciup.org/142215033
IDR: 142215033 | УДК: 517.98,
Текст научной статьи Свойства одной конечно-аддитивной меры на lp, инвариантной относительно сдвигов
Меры, инвариантные относительно сдвигов, успешно применяются при исследовании решений дифференциальных уравнений при помощи усреднения случайных блужданий в координатном пространстве. Практическое применение вышеописанных мер можно найти, например, в [9], [10] и [11]. В данных работах усреднение случайных однопараметрических семейств операторов сдвига на векторы координатного пространства по мерам на множестве таких операторов применяются для получения однопараметрических сильнонепрерывных полугрупп операторов, разрешающих задачу Коши для уравнения диффузии, уравнения дробной диффузии и уравнения Шрёдингера, с разнообразными гамильтонианами. Планируется в дальнейших исследованиях дифференциальных уравнений в бесконечномерных пространствах применить свойства, мер, установленные в настоящей статье.
Как известно (см. [6]), на. бесконечномерном топологическом векторном пространстве не существует аналога, меры Лебега, т.е. не существует такой нетривиальной меры, удовлетворяющей одновременно следующим свойствам:
-
1) борелевость,
-
2) счётная аддитивность,
©Бусовиков В.М., 2018
-
3) и-коиечиость.
-
4) локальная конечность,
-
5) инвариантность относительно сдвига на любой вектор этого пространства.
-
2. Построение меры
В силу несуществования нетривиальной меры, удовлетворяющей сразу всем перечисленным свойствам, изучались меры, инвариантные относительно сдвига на векторы из некоторого максимального допустимого подпространства, как в [7]. Или, например, не и-конечные меры, как в [5] или [8].
В данной статье изучаются свойства семейства мер на пространствах последовательностей 1р, удовлетворяющих свойствам 3)—5), изучавшиеся до этого в работах [1], [2], [3] и [4]. В частности, усиливается результат о верхней мере шаров из [4], в котором она вычислена только для шаров радиуса г < 2 и г > 1 в Z2- В разделе 4 будет вычислена верхняя мера шаров для всех радиусов в 1р, кроме гр = 2 1+ р. Вопрос о верхней мере шара радиуса гр остается открытым: известно только, что она равна либо 0, либо +то. Также до называется и-конечность меры на 1р, что не противоречит наличию континуума непересекающихся множеств единичной меры, как утверждалось в [3]. Наконец, приводятся некоторые технические результаты, не публиковавшиеся ранее.
Конечно-аддитивная мера А, о которой пойдет речь, была предложена В. Ж. Сакбаевым и наиболее подробно изложена в [1]. Для удобства читателя мы приведем здесь все необходимые определения и формулировки основных утверждений без доказательств. Также для удобства читателей все обозначения совпадают с данными в [3].
Под (а, 6) будем понимать конечный промежуток с концами а и 6 при а 6 6 и пустое множество при а > 6. При этом, если а = 6, множество (а, 6) может быть как одноточечным, так и пустым в зависимости от типа промежутка.
Теперь зафиксируем р Е [1, +то] и введем меру цр на 1р.
Определение 2.1. Назовем множество в 1Р брусом, если его можно представить в виде
{ж Е 1р | Vj Е N Xj Е (aj, 6j)}, а,6 Е 1^, и будем обозначать как Па,ь.
Определение 2.2. Брус Па,ь будем называть измеримым, если выполнено
∞
У^ ln(6j — а j ) Е [то, +то), j=0
и абсолютно измеримым, если
∞
У2 max{0, ln(6j — а j )} < +то.
j =0
Множество измеримых и абсолютно измеримых брусов обозначим за Ри Р а соответственно. Очевидно, что Ра С Р.
Определим следующую функцию на измеримых брусах: рр : Р ^ [0, +то):
/^р(Па,Ь) — *
exP E q ln(6j — d j ^ , Па,ь = 0, .0, Па,Ь — 0.
(1.1)
Заметим, что в 1^ никакой брус при 6 j > а j Vj не может быть пустым, а вот в 1р,р < то, непустота такого бруса эквивалентна условию с Е 1р, г де Cj — inf | x |.
х е^ а - ,b j )
Как видно из построения, др инвариантна на Р относительно сдвигов на векторы из 1р.
Также можно показать,
Лемма 2.1. Класс Л а класс мпоэіссстс К
что на Р она аддитивна (см. лемму 3.1 в [3]).
множеств вида П \
(й4
,п, Щ Е
Рг, является полукольцом,
конечных объединений из Л является минимальным кольцом,
содержащим Р. Элементы Л мы будем называть пористыми бру сами.
Доказательство см. в лемме 1 и 2 в [1].
Лемма 2.2. Функция рр однозначно продолжается до аддитивной неотрицательной функции на К. При этом она оказывается инвариантной относительно сдвигов на векторы из 1р.
Доказательство см. в леммах 3 и 4 в [1].
Определение 2.3. Для произвольного множества X С 1р введем верхнюю и нижнюю меры множества X:
К,(X) = sup Kp(R), р rek,rcx
К (X ) = inf кр (R).
р r к,с R
Определение 2.4. Множество из 1р будем называть измеримым относительно др, если p(X) = p(X), и его меру будем полагать равной [^(X ) = др(X) = p (X ).
Точно такую же конструкцию можно построить, взяв за основу не измеримые брусы, а абсолютно измеримые. Для этого рассмотрим ограничение функции д на Ра.
Лемма 2.3. Класс Ла множеств вида П\ U ТД , П, Щ Е Ра, является
\ 3=0 / полукольцом, а класс множеств Ка конечных объединений из Ла является минимальным кольцом, содержащим Ра.
Лемма 2.4.
Функция кр однозначно продолжается с
Ра до аддитивной
неотрицательной функции на Ка. При этом она оказывается инвариантной относительно сдвигов на векторы из 1р.
Доказательство дословно повторяет доказательства лемм 2.1 и 2.2.
Определение 2.5. Абсолютно аналогично введем для произвольного множества X С 1р верхнюю и нижнюю меры множества X:
pI(X) = suP Кр(Д), р Re^“,Rcx
К (X) = inf Кр(Пф р RERa,XCR р'
Определение 2.6. Множество из 1р будем называть измеримым относительно д“, если /“(X) = /“(X ), и его меру будем полагать равной /“(X ) = дp(X) = p“(X).
-
3. Некоторые технические свойства
В этом разделе мы поговорим о некоторых свойствах определенных выше мер, о способах посчитать нижнюю меру, о их связи с конечномерной мерой Жордана и о различиях между рр и др.
Начнем с тривиального факта, следующего непосредственно из определений.
Лемма 3.1. /“(X) 6 p(X)р и /“(X) > p(X)р для любого множества X С 1р.
Следствие 1. Если X абсолютно измеримо, то оно измеримо, и pp(X ) = д“(X).
Пользуясь этим, иногда мы будем говорить об обычной мере рр абсолютно измеримых множеств, подразумевая, что она равна д“.
Прежде всего заметим, что существует канонический изоморфизм lp = R" х l'p, разделяющий последовательность ж € 1р на конечную последовательность из первых п координат (ж1,..., жп) и бесконечную последовательность из оставшихся: (жп+1,жп+2,.. .)• При этом брус П а ,ь С l p можно представить в виде произведения п-мерного параллелепипеда со сторонами, параллельными осям координат, и бесконечномерного бруса. В дальнейшем мы часто будем пользоваться обозначением П = П' х П'' С R" х l'p, подразумевая под П' и П'' параллелепипед и брус соответственно. Как известно, такие п-мерные параллелепипеды образуют кольцо, и на них определена конечно-аддитивная функция, которая при пополнении, аналогичном проделанном в предыдущем пункте (определения 2.3 и 2.4), даёт меру Жордана, которую мы будем обозначать за pj.
Часто нам придется рассматривать не один брус, а их конечный набор, например Пі,...,Пп. В таком случае мы будем использовать двойные индексы, считая, что k-й брус из набора задается условиями Жj € kQ ',j ,b .,j )•
А теперь докажем одну техническую лемму, которая не раз пригодится нам в будущем для оценки нижней меры.
Лемма 3.2. В любом пористом брусе Q € Л можно выделить конечное объединение брусов из П мери, сколи угодно близкой к мере Q. То же самое остается верным, если заменить классы Л и П па Ла и П“.
(Д-)
Действительно, пусть Q = Qo\
■ где Q .
— (абсолютно) измеримые брусы.
Если /z(Qo) = 0, то утверждение очевидно, поэтому будем считать, что /z(Qo) > 0. Также без ограничение общности будем предполагать, что Q. = Q. П Qo.
п
Для бруса конечной меры Q . последовательность частичных сумм ^2 Wbkj — a . j ) з =1 ’ ’
∞ сходится с конечному значению, а хвост ряда ^2 ln(bk,j — a.,j) — к нулю, поэтому можно j=n+1
найти достаточно большое N, что при разложении бруса Q. в виде Q' х Q. С Rw х l'p мера N-мерного параллелепипеда Q' будет сколь угод но близка к мере Q., а мера Q' — к единице. Поскольку, в частности, мера Q'^ стремится к единице, при достаточно большом N мера бруса Q' х Q^ будет сколь угодно близка к мере исходного бруса Q . = Q' х Q .
п
Если же брус Q . имеет нулевуто меру, то ^2 ln(b.,j - Q ',j ) стремится к —то, и при j=1
достаточно большом N мера Q' будет сколь угодна близка к нулю (или и вовсе равна нулю, если b .j = a .j для иекоторого Д. Поэтому при большом N мера Q' х Q'^ будет сколь угодно малой.
Меру пористого бруса Q можно вычислить по формуле включений-исключений:
п п п п п п
MQ) = ^(Qo) — Е Др(Фг) + ЕЕ ^(Qt П Q j ) — ЕЕЕ ^(Q i П Qj П Q . ) + ... (3.1)
г =1 г =1 j =1 г =1 j =1 ' =1
Поскольку к каждому из брусов П, являющемуся пересечением брусов из конечного семейства Q1,... ,Qn, применимы все рассуждения, приведенные выше, можно подобрать такое натуральное N, что мера каждого из них будет отличаться от меры П' х Q'^ С Rw х l'p не более чем на. Qo\ ^^ Q' х Qo)
2щ. Тогда мера Q будет отличаться от меры пористого бруса не более чем на е, поскольку в фор муле (3.1) ровно 2п слагаемых.
Но последний можно представить как [Qo\ ^ U Q'^ ] х Qo € Rw х lp, a N-мерные параллелепипеды co сторонами, параллельными координатным осям, как уже говорилось, Г п \ образуют кольцо, т.е. Qo\ I U Q' ) можно представить конечным объединением таких '=1
m параллелепипедов: U Rm. В качестве заявленных в формулировке леммы брусов можно k=1
выбрать Rm х QQ.
Из этого мгновенно следует,что при вычислении нижней меры супремум можно братв не по элементам из ^, а по конечным объединениям брусов.
Лемма 3.3.
(и Qk.),
p(X) = sup p и QkCX,Qkер
(иQk).
pa(X ) = sup p
U Qkcx,Qkер “
То, что описанная мера pp строится очень похоже на меру Жордана в конечномерном случае, помогает иногда сводить утверждения к конечномерному случаю и пользоваться готовыми утверждениями для последней. Например, при помощи следующей леммы.
Лемма 3.4. Множество X = W х И С Rn х I’, где П — (абсолютно) измеримый брус (абсолютно), измеримо, если и только если W измеримо ио Жордану, и его мера равна pj(W ) •pp (П).
Если W — параллелепипед со сторонами, параллельными координатным осям, то формула pp(X ) = pj(W ) • pp(n), очевидно, выполнена.
Пусть X = W х П С Rn х 1р, где W - множество, измеримое по Жордану. Тогда V e > 0 существуют множества Ае и Ве, являющиеся объединением конечного количества п-мсриых параллелепипедов, такие что Ае С W С В£ и pj (Ве) — pj (Ае) < е. II поскольку Ае х П и Ве х П лежат в ^ и их меры равны pj (Аe)pp(П) и pj (Вe)pp(П) соответствеппо. то множество X измеримо, и его мера, равна, pj (W) • pp(n).
Обратно, пусть X = W х П измеримо относительно меры измеримого множества, и леммы 3 следует, что есть конечное пm pp. Из определения объединение брусов
(3 . 1)
х R'^ С Rn х ip. При
Q = U Qk 11 пористый брус R = Rq\ I [J Rk I. такие что k=1k=1 /
Q С X С R, p p( R ) — p p( Q ) < е.
пm
Представим их в виде J Q'k х Qk С Rn х l'p ii RQ х RQ'\ I J R'k к=1к=1
этом Qk С П Vk = 1,п, поэтому Qk можно заменить на Qk х П без нарушения условий (3.1). Объединение Qk обозначим за Ае.
Аналогично, можно заменить Rq на RQ х П, a Rk (при к > 0) на Rk х (R’k О П). Теперь заметим, что при к > 0 Rk О W = 0, поскольку в противном случае X и Rk имели бы непустое пересечение, и X не содержался бы в R. Но тогда X О (Rk х П) = 0, поэтому X С [rq \ ^ U Rk^j х П = Ri, и pp(Ri) 6 pp(R). Как и в предыдущем рассуждении, (m \
U Rk I в виде копечік>го объединения п-мерных параллелограммов Ве. k=1
Мы получили, что Ае С W С Ве, и pj (Ве) — pj (Ае) < ^-^щ, т-е- W будет измеримым по Жордану и иметь меру ^ p ( ^) •
Для верхней меры доказатв удобный критерий, как в лемме 3.3, не удается, но зато еств следующее достаточное условие того, что множество имеет бесконечную верхнюю меру.
Лемма 3.5. Если непустой брус П а,ь измерим, но не абсолютно измерим, то ^“(П„,Ь) = 0, Д“(Пад) = +то. ’
Разобьем множество координат на два множества: N = I+ U I- по правилу j Е I+, если ∞
^ з - а з > 11 и j Е I- в противном случае. Если ряд 52 Wby — a, j ) сходится условно, то з = 1
52 ln(b3- — cij) = +то и 52 ln(b3- — cij) = —то. Пусть брус Па',у С Пад абсолютно измерим, 3^1+ 3^1- тогда 52 ln(b3 — °3') 6 ^ ^(by — aj) = -то. При этом из условия абсолютной измеримости 3ЕІ- 3ЕІ- следует, что мера хотя бы одного из рядов 52 ln(b3 — а3-) и 52 ln(b3 — а3-) должна быть 3^1- з^1+ конечна. Значит, 52 ln(b3 — а3) < +то, и р?(Па‘,ь‘) = 0. Вместе с леммой 2 это означает, КГ ■ что р“(Па,ь) = °
Аналогично, предположим, что Д“(Пад)) < +то, тогда Пад лежит в конечном объединении абсолютно измеримых брусов Qam,bm конечной меры. Заметим, что для каждого из этих брусов существует только конечное число координат из j Е I+, для которых а- + -^ Е (аД,ЬД) и b- — -^ Е (аД, ЬД), т.к. в противном случае 52 1п(ЬД—аД) = +то, что противоречит конечной измеримости. А это значит, что найдется jei+ такая точка с к-й координатой в множестве [а- + -д, bk + -д}, которая не покрывается никаким брусом из Qam,bm, но она, очевидно, лежит в Пад.
-
4. Верхние и нижние меры шаров
В этом разделе мы найдем меру шаров для почти всех радиусов для каждого р. Теорема 4.1 усиливает результат, полученный в статье [4], в которой найдены меры шаров с радиусами г < 2 1і г > 1.
Шар радиуса г в l ? обозначим за В ? Все утверждения ниже справедливы и для замкнутых, и для открытых шаров.
Поскольку в l? шары являются брусами, то вычисление их мер не составляет труда.
Лемма 4.1. В? = {х Е l? | Vj Е N Xj Е (—г, г)}, поэтому f 0,
ьСВ )= ^(вп = {1,
+то ,
г < г = г >
2 ,
2 ,
2 •
Ситуация с шарами в 1 ? ,р < то обстоит несколько сложнее. Покажем для начала, что нижняя мера любого шара равна нулю.
Лемма 4.2. Vp Е [1 , +то) V г > 0 р? ( В? ) = р“ ( В? ) = 0.
Доказательство следует из леммы 3.3 и из того, что если П а , ь С В ? т о b 3 — а 3 ' '-А 0.
Также, в отличие от случая р = то, при р < то верхняя мера В? может быть равна только нулю и бесконечности.
Лемма 4.3. Если Д?(В?) конечна, р Е [1, то), то р?(В?) = 0. Аналогично, если р“(В?) конечна, то р?(В?) = 0.
Если В? имеет конечную верхнюю меру, то он содержится в конечном объединении п измеримых брусов и Qk х Q- С Rm х l'p. Поскольку проекция В? на первые т координат к=1
— это шар радиуса г по р-норме в Rm, мера которого стремится к нулю при увеличении п размерности, то В? будет лежать в множестве U B?|r х Q-, которое по лемме 3.4 будет к=1 m измеримым. При увеличении т мера Вр^ будет стремиться к нулю, а мера бД — к единице, а значит, цр(Вр) = 0.
Доказательство для цр проводится аналогично. ■
Теорема 4.1. Для всех р Е [1, +то)
при Т < Тр
Цр(БП = РР(БП = 0, при Т > Тр
Др(БР) = ^(В?) = 0, Цр(ВР) = цР(ВР) = +то, где тр = 2 р
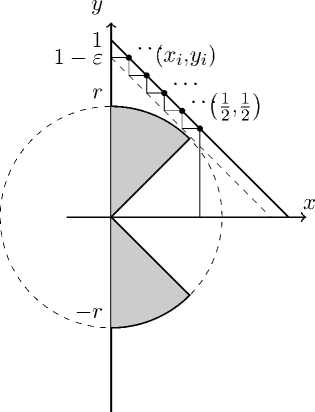
Рис. 1. Множество Х2 и строительство покрытия шара радиуса В2
С учётом лемм 4.2, 4.3 и 3.1 для доказательства этой теоремы необходимо доказать два факта: р р (Вр ) < +то пр и т < тр и рр (Бр ) = +то пр и т > тр. Начнём с первого из них.
Рассмотрим произвольный элемент z Е Ір. Поскольку zj стремится к нулю при у ^ то, то максимум |zj | достигается при некотором индексе J. Отложим на двумерной плоскости по оси ординат zj (с учетом знака), а по оси абсписс — max Izj|. Образ Вр при таком j=j отображении представляет собой пересечение двумерного шара радиуса т по р-норме и конуса, заданного неравенствами 0 6 ж 6 |у|. Обозначим его за Хр. Пример такого множества для случая І2 представлен на рис. 1.
Проведём прямую у + ж = 1. Поскольку т < тр, т.е. т < || (2, 2) ||р, она не пересечет Хр. Проведём параллельную ей прямую ж + у = 1 — Е. пересекающуюся е Хр не более чем в одной точке (это возможно сделать, поскольку Хр выпукл о; при р > 1 можно провести касательную к шару радиуса т по р-норме), и построим «лесенку», как показано на рис. 1, начинающуюся в точке (2, 2). Занумеруем точки её пересечения с верхней прямой:
N
{(ж іЕ У г ) }^ и рассмотрим объединение брусов J (П -Хі , Уі U П-№А). Нетрудно видеть, что г =1
они абсолютно измеримы и имеют единичную меру. Покажем, что они содержат в себе Вр.
Действительно, пусть z Е Бр. Пусть сначала максимальный по модулю элемент zj положителен. По построению, найдется точка (ж^, уД такая, что соответствующая z точка
(zj, max Iz j |) Е R2 лежит внутри прямоугольника [0, ж^] х [0, уД. Тогда z j Е [0, у^] С [—ж^, уф з = ]
и при з = J выполиево Iz j | Е [0,ж«] ^ z j Е [—ж«,жг] С [—ж«,уг], т.е. z Е П-Жі,Уі. Если же
максимальный по модулю элемент z j отрицателен, то Докажем теперь, что цР(Вр) = +то пр и т > тр.
—z Е П-Жі , Уі,
И z Е В-у^.
За ві обозначим элемент 1р, у которого Тя координата равна единице, а остальные — нулю.
Предположим, что для некоторого шара радиуса г > гр найдено покрытие, состоящее из конечного количества измеримых брусов: Qj,к = 1,К. Для некоторого достаточно малого е точки вида (2 + е) ві — (2 + е) ej будут лежать в В?. Значит, каждая из них должна лежать и в каком-то из указанных брусов.
Для конечного набора брусов найдется такой номер N, что при п > N их длины по п-й координате не будут превосходить 1+ е, то есть ника кой интервал (а&,„, bj,n), участвующий в определении бруса, не может содержать точки (2 + е) en и — (2 + е) еп одновременно. Для каждого бруса составим бесконечную двоичную последовательность q^+iqj +2^at +3 • • •>гДе qj = 0, если к-й брус содержит точку — (2 + е) еп или ни одну из них, и qi = 1 иначе. Тогда из того, что (2 + е) ei — (2 + е) ej Е Hj, следует, что (q^ = 0) и (qj = 1).
Мы получили, что ^i,j > N найдется брус (за номером к), чья последовательность удовлетворяет условиям (qj = 0) и (qj = 1). Покажем теперь, что таких конечных наборов двоичных последовательностей не существует. Действительно, пусть мы нашли наименьший по количеству содержащихся в нем последовательностей набор qj, удовлетворяющий этому условию. Возьмем любую (первую) последовательность из этого набора. Она содержит бесконечное число единиц или бесконечное число нулей. Следовательно, можно выбрать такую подпоследовательность натуральных чисел щ, что двоичная последовательность для этого бруса qj. станет тривиальной, т.е. состоять из одних нулей или из одних единиц. Переходя одновременно к подпоследовательностям q„., получим, что они также удовлетворяют исходному условию, но из них можно выкинуть первую последовательность без потери этого свойства, т.к. для тривиальной последовательности (qj = 0) и (qj = 1) не могут быть выполнены ни для каких г и j. Противоречие.
-
5. Возвращаясь к теореме Вейля
Теорема 5.1. Мери рр и цр нри р Е [1, +то) обладают свойствами, заявленними на рис. 2.
|
Р р ,р Е [1, +то) |
цр,р Е [1, +то) |
|
|
борелевость |
_ |
_ |
|
счётная аддитивность |
- |
- |
|
ст-конечность |
+ |
+ |
|
локальная конечность |
+ |
+ |
|
инвариантность относительно сдвигов на векторы из 1р |
+ |
+ |
Рис. 2. Свойства мер рр и рр
Отсутствие борелевости и наличие локальной конечности следует из теоремы 4.1 об измеримости шаров. Наличие ст-конечности и отсутствие счетной аддитивности можно показать, предъявив счётное семейство абсолютно измеримых брусов нулевой меры, покрывающих все 1р.
Например, пусть Qp ,b (n, С),п,С Е N, задается следующим образом:
_ j —С, j 6 п, Qj =
— 4, j >п, Очевидно, что 1р
b
=
U Q a,b (n,C ) II п,С
j 6 п, j > п.
^ p. (Q a,b (n,C ))
= 0, а также, что любой брус
положительной меры можно представить в виде счетного объединения брусов меры нуль,
взяв пересечения с Qp ,b (n,C ).
Инвариантность относительно сдвига на векторы из 1р следует из определений верхней и нижней меры и того, что аддитивная функция цр, определенная на брусах по формуле (1.1), инвариантна относительно сдвигов.
Заметим в заключение, что отсутствие счётной аддитивности является в каком-то смысле неустранимым дефектом. Например, в [1] показано, что при применении схемы Лебега-Каратеодори к рр полученная счетно-аддитивная мера будет тождественно равна нулю.
Замечание. Отметим работы Бейкера и Завадского (см. [5] и [8] соответственно), в которых изучались трансляционно-инвариантные меры на 1^, свойства которых существенно отличаются от свойств мер из теоремы 5.1. А именно, в указанных работах установлено, что трансляционно-инвариантная мера на 1^ обладает свойством счетной аддитивности, но не обладает свойством и-конечности.
Автор благодарит В. Ж. Сакбаева за плодотворное обсуждение затронутых в работе проблем.
Работа выполнена при поддержке проекта 5-100 повышения конкурентоспособности ведущих российских университетов среди ведущих мировых научно-образовательных центров.
Список литературы Свойства одной конечно-аддитивной меры на lp, инвариантной относительно сдвигов
- Сакбаев В.Ж. Меры на бесконечномерных пространствах, инвариантные относительно сдвигов//Труды МФТИ. 2016. T. 8, № 2. С. 134-141.
- Сакбаев В.Ж. Конечно-аддитивные меры на банаховых пространствах, инвариантные относительно сдвигов. Квантовая динамика и функциональные интегралы//Материалы научной конференции ИПМ им М.В. Келдыша РАН. Россия. Москва, 14 марта 2016 г. M.: ИПМ им. Келдышa, 2016.
- Сакбаев В.Ж. Случайные блуждания и меры на гильбертовом пространстве, инвариантные относительно сдвигов и поворотов//Дифференциальные уравнения. Математическая физика, Итоги науки и техн. Сер. Соврем. мат. и ее прил. Темат. обз. 2017. 140. М.: ВИНИТИ РАН, 2017. 88-118.
- Сакбаев В.Ж. Усреднение случайных блужданий и меры на гильбертовом пространстве, инвариантные относительно сдвига//ТМФ. 2017. Т. 191, № 3.
- Baker R. «Lebesgue measure»on �∞//Proceedings of the AMS. 1991. V. 113, N 4. P. 1023-1029
- Вейль A.Интегрирование в топологических группах и его применение. М.: Изд. иностр. лит., 1950.
- Вершик А.М. Существует ли мера Лебега в бесконечномерном пространстве? Анализ и особенности. Часть 2, Сборник статей. К 70-летию со дня рождения академика Владимира Игоревича Арнольда, Тр. МИАН, 259, Наука, МАИК «Наука/Интерпериодика», М., 2007, 256-281; Proc. Steklov Inst. Math., 259 (2007), 248-272
- Завадский Д.В. Инвариантные относительно сдвигов меры на пространствах последовательностей//Труды МФТИ. 2017. Т. 9. № 4. С. 142-148.
- Борисов Л.А., Орлов Ю.Н., Сакбаев В.Ж. Формулы Фейнмана для усреднения полугрупп, порождаемых операторами типа Шредингера//Препринты ИПМ им. М.В. Келдыша. 2015. № 057. 23 с.
- Смолянов О.Г., Шавгулидзе Е.Т. Континуальные интегралы. М.: УРСС, 2015.
- Орлов Ю.Н., Сакбаев В.Ж., Смолянов О.Г. Неограниченные случайные операторы и формулы Фейнмана//Изв. РАН. Сер. матем. 2016. № 80:6. C. 141-172; Izv. Math. 2016. N 80:6. P. 1131-1158.


