Свойства сходимости по мере на йордановых алгебрах
Автор: Ганиев Иномжан Гуломжанович, Каримов Абдусалом Кодиралиевич
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 4 т.5, 2003 года.
Бесплатный доступ
В работе продолжается изучение свойств топологии сходимости по мере на йордановых алгебрах. Дается явный вид метрики на йордановой алгебре, которая определяет топологию сходимости по мере.
Короткий адрес: https://sciup.org/14318096
IDR: 14318096 | УДК: 517.98
Текст научной статьи Свойства сходимости по мере на йордановых алгебрах
В работе продолжается изучение свойств топологии сходимости по мере па Йордановых алгебрах. Дается явный вид метрики на Йордановой алгебре, которая определяет топологию сходимости по мере.
В работах [1-3] было введено понятие OJ-алгебры и изучены свойства, этих алгебр. В частности, OJ-алгебру можно рассматривать как объект, описывающий в аксиоматической форме пространство измеримых элементов относительно ЛЛУ-алгебры. В [1, 2] рассматривалась также топология сходимости по мере, в частности, в [1] доказано, что в этой топологии OJ-алгебра является топологическим кольцом. В [2] рассмотрена R топология на. О J-алгебрах, описаны условия ее существования, единственности и метризуемости.
В настоящей работе продолжается изучение свойств топологии сходимости по мере на. Йордановых алгебрах. Дается явный вид метрики на. Йордановой алгебре, которая определяет топологию сходимости по мере. В случае алгебр фон Неймана, аналогичный вопрос рассматривался в работе [6].
Пусть (А, || • ||) — ЛЛУ-алгебра. с точным нормальным конечным следом т, S(A) — OJ-алгебра измеримых элементов относительно А (см. [1]).
ОПРЕДЕЛЕНИЕ 1. Элемент a Е S(A) назовем т-измеримым если в спектральном + оо разложении a = J Xde\ идемпотенты щ ■ и е_\ имеют конечную меру т. е. т(е;Д) < сю — схэ и т(е_д) < сю при некотором А. Через К(А) обозначим множество всех т-измеримых элементов из S(A).
Определение 2. Для любого a Е КД^ значения функции
а(а) = inf{A Е [0, сю] : т(1 — ед) Сф (а > 0),
СХЭ ____ где а = J Xde\, а = Va?, называются обобщенными s-числами элемента, а. Через «о» о обозначим йорданово произведение в S(A).
Предложение 1. Имеют место следующие утверждения:
-
(1) функция а (а) невозрастающая, непрерывная справа и
- Нта(а) = ||а|| Е [0,сю], a Е К^А);
аДО
-
(2) для любой строго возрастающей непрерывной функции g на [0, оо) такой, что у(0) ^ 0 имеет место
9(Ы)(«) = у(|а|(а)), при всех a Е Кфф a > 0;
-
(3) а(а) = 0 для a ^ r(supp а|) и для любого a Е К фр
-
(4) а(а) = а|(а) и фффр = /3|а(а), где а Е КфР Р Е Ж, а > 0;
-
(5) (а + Ь)(а + /3) < а(а) + Ьф^ для всех a,b Е Кф) и аф > 0;
-
(6) а(а) < Ьфф если 0 < а Д 6. а > 0;
-
(7) (а о Ьфф ^ ||6||а(а) для всех а Е Кф^, b Е А.
ОО
-
(8) если а Е А, а р 0, то тф) = Уа(а) da, в частности,
о
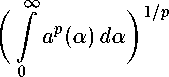
-
(9) если a,b Е А, то
tt
' /((а + ффР da ^ / /(а(а) + Ьф)) da (I > 0)
для любой возрастающей непрерывной выпуклой функции f;
-
(10) если / возрастающая вогнутая функция на [0, оо] и /(0) = 0, то
tt
t
I рффУ) da.
/ /((а + Ь)ф) da ^ / /(а(а))
оо
-
< (9): Рассмотрим JBPP-алгебру Лф,ф, порожденную элементами а и Ь. По предложению 3.9 [3, стр. 26] она изоморфна обратимой ЛР-алгебре. Тогда след т можно продолжить до обертывающей Лфф алгебры фон Неймана W(Лф,Ь)) . Из единственности спектрального семейства следует, что s-числа для элементов а и b в Wфф,bY и в Лф,ф совпадают, поэтому требуемое неравенство, справедливое в Wфф,bY в силу [4], верно и в Лф, ф.
Остальные утверждения предложения 1 доказываются аналогично. >
ОПРЕДЕЛЕНИЕ 3 (см. [1]). Топологией сходимости по мере на Кф) называется отделимая векторная топология t, в которой базис окрестностей нуля образуют множества вида Кфф) ф,б > 0), где
Кфф) = {а Е Кф) : Зр Е V ,Upa Е А, ||1/ра|| < Е,тфф < бф
Здесь Up : Кф) —> Кф) — линейное отображение, определяемое равенством
Пжу = 2ж о ф о у) — ж2 о у.
V — булева алгебра всех идемпотентов в А. Если А специальна, то Uxy = хух, где ху — ассоциативное произведение элементов х и у.
Сходимость в топологии t обозначим как а„ Д а и назовем ее сходимостью по мере.
Предложение 2 (см. [5]). Если an,a Е К^А), то справедливы утверждения:
-
(i) an Д а тогда и только тогда, когда (а„ — а)(а) —> О (а > О);
(п) если an Д а, то /(а„) Д /(а) для любой действительной непрерывной функции /.
Отделимую векторную топологию ш на К^А^ будем называть ^-топологией, если выполняются следующие условия:
-
1 .(1) для любой окрестности нуля W существует окрестность нуля V С W такая, что из 0 < ж < у Е V, следует х Е V;
-
(2) если у Е V, s2 = 1, р Е V, то Us^y^ Е V и Up(y) Е V (такие окрестности V называют нормальными), где 1 — единица алгебры К(А);
-
II. для любой сети идемпотентов {еа}, убывающей к нулю, еа Д 0;
-
III. если {еа} С V, еа Д 0, то для любой сети {жа} элементов из К (А) сеть {жа о еа} сходится к нулю в топологии ш.
Предложение 3 (см. [2]). В топологической OJ-алгебре (К(А),ш) справедливы утверждения:
-
(1) R- топология ш совпадает с топологией сходимости по мере;
-
(2) ш метризуема тогда и только тогда, когда К (А) счетного типа.
Теорема 1. Отображение р : А х А —> [0, оо), определенное равенством
Р^,у^
т
\х-у\ \
1 + к -у|/
является метрикой на А.
< Проверим аксиомы метрики.
-
1) Очевидно, что р^х,у^) ^ 0. Если р^х,у^) = 0, то в силу точности т получим, что ^—^—г = 0, т. е. ж = у. Обратно, если ж = у, то, очевидно, р(ж, у) = 0.
-
2) Очевидно.
-
3) Пусть х,у Е А, тогда. р^х,у) = т
^ da. Так как
функция /(1) = -^ £ / возрастает, непрерывна, на. [0,+оо) и /(0) = 0, то из предложения 1(2) следует, что
ОО ОО рД,у) = I ^ ^^ da =
J 1 + |®-у|(«)
гг
J 1 + (ж —у)(а) J 1 + (х — г + г — уда) оо
Далее, из утверждения (10) предложения 1 следует, что
P^,y^
/ (ж —Д(а) f (z — у)(а)
-----—- da + ————- da = р(ж, z) + р)у, z).
1 + (ж-г)(а) у l + ^z-уфа) оо
Теорема, доказана. >
Через П обозначим отделимую топологию в А, порожденную метрикой р. Покажем, что П наделяет А структурой топологического векторного пространства. Так как р^х— у),0) = р(ж,у), то операция сложения непрерывна, в топологии Д. Пусть А„ —> А, А„,А Е ж Е А. Тогда.
р((А„ - А)ж,0) = |А„ - A rf *Ж* < |А„ - А|т(|ж|) -д 0.
\1 + А„ - А| |ж| /
Следовательно, Апж ^ Аж. Пусть ж„ ^О, жп£ А, А„ G 1, А„ < 2т (п = 1,2,...). Тогда
■п^П)
0) = т
А„||жп А
1 + |АД|жД >
/ 2т|ж„ А
VI + 2т|ж„|/
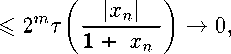
-
т. е. Апж„ ^ 0.
Аналогично, если ж„ Д ж, то Аж„ Д Аж для всех A G R.
Отсюда и из равенства Апж„ — Аж = А(ж„ — ж) + (А„ — А)ж + (А„ — А)(ж„ — ж) следует, что операция умножения на скаляр непрерывна в топологии Н-
Предложение 4. Топология Н на А является R топологией.
< I. (1): Пусть 0 < ж < у и р(у,О) < Е. Так как функция /(а) = । “ а возрастающая, а след т положителен, то
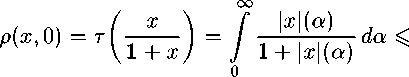
Уи\И
1 + Ы (°0
da = р(у, 0) < Е.
(2): Так как любая двухпорожденная подалгебра специальна, то при р(у, 0) < е, р G V выполнены равенства
р(1фж,0)
/ |ржр А Г (ржр)(а) т I ------------] = / -----------------
Vl + фжрД J 1 + (ржр)(а) о
da
Г |М|2ж(Д / |ж| А
J 1 + ||<ж(а) U + ИУ
= Дж,0) < е.
Аналогично, если s2 = 1, то р(П5ж,0) < Е.
II: Пусть еа ^ 0. Тогда. р(еа, 0) = т I 1 ®“ ) = 7т(еа) -Д 0, т. е. еа 4 0.
III: Пусть {еа} CV, еа^ 0, т. е. р(еа,0) —> 0. Тогда.
± / \ / са
—т eQ = г ---- 2 k ; \ 1 + ,
а
Так как
1 + |a;Q о еа| '
то для ха Е А будет
Отсюда, выводим
^q |*^q 0 ^а | ^а
1 + |^а ° еа|
р(ха 0еа,0)
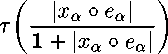
= т
^а |*^а
1 +
0 ^а |^а
< т(еа) -Д 0,
т. е. жа о еа Д- 0. Следовательно, Н является R топологией на. А.
Из предложений 3 и 4 следует, что топологии t и Н совпадают на. А.
Известно (см. [1]), что А плотно в OJ-алгебре К^А^ т-измеримых элементов, присоединенных к А, относительно топологии сходимости по мере, т. е. можно считать, что
К^А) есть замыкание А в топологии t. Поэтому р продолжается до метрики р на K^AY порождающей топологию t.
Предложение 5. Пусть an Е А, ||а„|| < 1, а„ Д а. Тогда. т(ап) -Д т(а).
-
< Пусть а = 0, е > 0. Тогда существуют номер п(е) и р Е V такие, что ДрД < | и ||7фа„|| < | для всех n > n^Y Если а„ = а„ о s„ полярное разложение а„, где s„ — симметрия в А (т. е. s^ = 1, ||s„|| = 1), то
Мап) < т(|а„|) = т(|а„ ор + \ап\ орД = т(ап о su op) + т(а„ о s„ ор1) < ||8„||т([/рап) + ||а„||||8„||т(р±) < ||Е7ра„|| + т(рД < | + | = е,
-
т. е. т(а„) —> 0 при п -Д оо.
Теорема 2. Метрика, р имеет вид р^х^) = т( У* (ж,уЕК(Л)).
\1 + к - у\)
-
< Пусть ж, у Е К)А) и ж„, yn Е А, такие что ж„ Д ж, у„ Д у. Тогда. ж„ -Д х, уп -Д у в JR-топологии. Из предложения 2 следует, что
- к» - у» Е к ~ у!
1 + |ж„-у„ 1 + |ж-уГ т. е.
kn - Уп Д |ж - у|
1 + |ж„-уп 1 + к~УГ
Так как 0 < ^"--^—г < 1, то в силу предложения 5
т
к» - Уп
1 + |ж„ - Уп
-4- Т
к-у| А
1 + |ж - у|У
Из
р(ж,у) = Нтр(ж„, у„) = Нтт п п
kn-уп А ( \х-у\ \
-------------------- I = т I I
1 + |ж„-Уп|/ \1 + \х-у\;
следует, что
Р^,у)
к-у| \
1 + к - у1/
Теорема, доказана. >
Пусть Л-обратимая ТИ^-алгебра (т. е. йордонова алгебра, ограниченных самосопряженных операторов в гильбертовом пространстве), т-точный нормальный конечный след на. А, К(А) — OJ-алгебра т-измеримых операторов, присоединенных к A, W(A)- обертывающая алгебра, фон Неймана, для А. Продолжение т до W(A) является точным нормальным конечным следом т^ (см. [3]). Через K^W) обозначим кольцо тц-измеримых операторов присоединенных к алгебре W(A) . Ясно что, К(А) С K(W).
Следствие. Пусть xn, х Е К^А) ^n = 1, 2, 3,... ). Тогда. хп сходится по мере к х в К (А) тогда, и только тогда, когда. хп сходится по мере к х в K(W).
Теорема 3. Метрика, р обладает следующими свойствами:
-
(1) р(ж + у, 0) = р^х, 0) + р(у, 0), где х,у Е А+ = {ж Е Л : ж > 0}, жу = 0;
-
(2) р(Ле,О) = Л^р(е,0), A G R, е G V;
-
(3) р^х о е, 0) < х ^^ц Ф, 0), х G А, е G V;
-
(4) если a G А, х G K^AY то существует такое натуральное число п, что
- р(а о ж, 0) < 2пр(х,0);
-
(5) если s Е А и s2 = 1, то p^Usx, Ц^у) = p^x,yY
< (1): Пусть ж, у G А' . ж о у = 0. Тогда ж о (1 + ж + у) = ж + ж2 = ж о (1 + ж) и у о (1 + ж + у) = у + у2 = уо(1+у). Отсюда ж ж у у
1+ж 1+ж + у’ 1+у 1+ж + у’
1 + ж + у 1 + ж 1+у
Следовательно,
. х / ж + у А / ж A / у А , х , у ж + у,0 = т ——— = т —— +т —— = у ж, 0 + р у, 0 .
\1 + ж + у/ \1+ж/ \1 + у /
(2): Так как (|А|е)/(1 + А|) = (|А|е)/(1 + А|е) и т(е) = 2у(е,0), то
у(Ае,0) = т
= т
е
(3): Пусть ж G А и е G V. Тогда
у(ж о е, 0) = т
т\ о е) J о
о
= ^Ф
Г _С№М^)_
У 1 + (||ж||е)(а) о
da =
о
2Щ ., m
, I! |Л+0)-
(4): Пусть а Е А, х Е К(А). Выберем такое натуральное число п, что ||а|| < 2П. Тогда р^а о ж, 0)
т
ОО а ° ж А Г
1 + |аож|у J о
а о ж
1 + а о ж
ОО
(а) da = J о
а о ж (а)
1 + а о ж (а)
da
(5): Так как
Г 2пж(а)
J 1 +2пж(а) о
ОО da Г / 1 . da = 2пр(ж,0).
У 1+ж(а) м ' о
П5ж|2 = 8Жб|2 = (еже) О (еже) = б|ж|28 = 8|ж||ж|8 = б|ж|8 О б|ж|8 = (1/5|ж|)2,
ТО П5Ж = фж!. Поэтому
p _ / \Usx-Usy\ А _ "T\l + \Usx-Usy\) "У о \Usx - Usy\ l + \Usx-Usy\ (a) da 1 + |СУДж - у) | / (a) da 1 + С^ж - у (а) da б|ж - y|s 1 + 8|ж — y|s (а) da ОО j^-^H^ + ^-^PWda О оо f^-^WW^-dW'XW- О оо j^-WAW + ^-^OXA™ О оо оо У'(8|ж-у|(1 + |ж-у|)-15)(а)^ = j (з о о (а) da Теорема доказана. > Авторы благодарны профессору В. И. Чилину за полезное обсуждение результатов.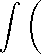
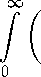
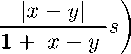
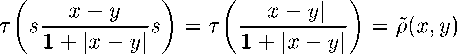
Список литературы Свойства сходимости по мере на йордановых алгебрах
- Аюпов Ш. А. Интегрирование на йордановых алгебрах//Изв. АН СССР. Сер. Матем.-1983.-Т. 47, № 1.-С. 3-25.
- Аюпов Ш. А., Усманов Ш. М. Порядок и топология в йордановых алгебрах.-М., 1980.-75 с. Деп. в ВИНИТИ № 4232-80.
- Аюпов Ш. А. Классификация и представление упорядоченных йордановых алгебр.-Ташкент: Фан, 1986.-124 с.
- Fack T., Kosaki H. Generalized s-numbers of \tau-measurable operators//Pac. J. Math.-1986.-V. 123, № 2.-Р. 269-300.
- Каримов А. К. Субаддитивные меры на йордановых алгебрах//Узб. мат. журн.-1993.-№ 4.-С. 42-47.
- Ганиев И., Чилин В. И. Измеримые расслоения *-алгебр измеримых операторов//Узб. мат. журн.-2001.-№ 1.-С. 8-13.


