Свойства сложно-периодических неоднородных систем в радиочастотных и оптических направляющих структурах

Создание периодических структур в направляющих системах радио- и оптического диапазонов открывает широкие перспективы для формирования на их основе информационно-измерительных систем мониторинга физических полей и параметров материальных сред. Периодические структуры с эффектом брэгговского отражения, воплощенные в оптическом волноводе и радиочастотном коаксиальном волноводе, имеют схожие преобразовательные свойства, что позволяет проводить аналогии и находить новые области применения указанных структур. В оптическом диапазоне волоконные брэгговские решетки (ВБР) характеризуются периодическим возмущением показателя преломления сердцевины волоконного световода, при этом период решетки определяет резонансную длину волны структуры. В радиочастотной области аналогом ВБР можно считать брэгговскую структуру в коаксиальном кабеле (БСКК), представляющую собой расположенные в коаксиальном волноводе периодические неоднородности волнового сопротивления. Формирование нерегулярностей в поперечных сечениях БСКК возможно введением ячеек во внешнем проводнике и диэлектрическом заполнении коаксиального кабеля. Измерительные характеристики датчиков, основанных на преобразовательных свойствах ВБР и БСКК [1; 2; 14; 15], могут быть улучшены посредством организации сложного профиля для закона периодичности структуры. К таковым можно отнести структуры, однородная периодическая конфигурация которых содержит фазовый дискретный сдвиг.

1. Периодические структуры с фазовым сдвигом в оптическом диапазоне

ВБР с фазовым сдвигом и только фазовой дискретизацией привлекают все большее внимание разработчиков сенсорных систем [3–7], поскольку могут быть изготовлены с помощью простых фазовых масок с минимальными требованиями, предъявляемыми к параметрам модуляции коэффициента преломления и равномерности характеристик его профиля [8].

Реально достижимая полуширина резонансного спектра ВБР в конфигурации интерферометра Фабри-Перо (ИФП) составляет по данным [9] 0,025 нм, а для классической ВБР – 0,5 нм. Это значит, что разрешающая способность ИФП сенсора в 20 раз лучше, чем у датчика на одной ВБР. Развивая данный подход можно использовать для создания сенсоров ВБР с фазовым дискретным сдвигом на π , которая представляет

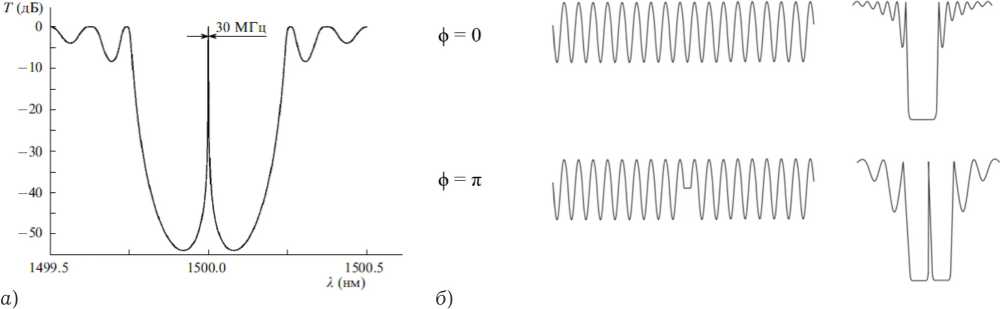
Рис. 1. Спектр пропускания ВРБ с фазовым сдвигом п в середине

собой простейший ИФП с длиной резонатора, не превышающей длину волны Брэгга X в .

ВБР с фазовым сдвигом, в частности равном п (рис. 1, а ), отличается наличием сверхузкополосной зоны пропускания, размещенной при определенных условиях на брэгговской длине волны решетки.

В общем случае ВБР с фазовым сдвигом характеризуется неоднородностью с размером от 0 до 2 п , расположенной в определенном месте ее структуры по длине. На рис. 1, б показаны случаи для ф = 0 и ф = п с размещением неоднородности на брэгговской длине волны.

Полуширина резонансного пика такого типа решеток может достигать 0,005 нм [10], что свидетельствует о возможном увеличении разрешающей способности измерений по температуре и линейному натяжению в 10–50 раз по сравнению с датчиком на классической ВБР. При измерении изгибного натяжения однородная периодическая структура ВБР преобразуется в чирпированную, что эквивалентно одновременному появлению фазовой с переменным шагом и амплитудной по закону Гаусса модуляции ее коэффициента преломления. Применение фазового дискретного сдвига на п в структуре чир-пированной решетки позволяет получить более интересный эффект, заключающийся в уширении зоны пропускания при изменении величины изгибного натяжения без изменения значения длины волны Брэгга X в , т. е. с исключением зависимости измерения изгибного натяжения от температуры.

Для математического моделирования спектральных характеристик ВБР применяются различные методы, включая метод матриц передачи [11], метод матриц Джонса [12], метод связанных мод [1]. Получение наиболее точных спектральных характеристик ВБР с фазовым

сдвигом при их равномерном растяжении/сжа-тии возможно при использовании метода связанных мод [1]. Наибольшее приближение к реальным характеристикам ВБР, подверженных изгибному натяжению, получают с помощью метода матриц передачи для отрезков до и после изгиба и с учетом линейного изменения этих отрезков по градиенту изгиба [11].

Модуляция коэффициента преломления равномерной ВБР представляет собой синусоидальный процесс с постоянной амплитудой, который может быть записан следующим образом

n ( z ) = n co + A n cos ⁽— z +ф ( z ) а для ф ( z ) = п примет вид

n ( z ) = -

no

no

.      (2пп)

+ An cos    z +

(Л

(2пп)

+ An cos    z -

1Л

z < 0

z > 0.

Рассмотрим две встречных волны A_i и B_i , распространяющиеся в волокне через ВБР [ 0, z 2 ] с длиной волны X , где i = 1,2 зависит от участка распространения волны (до или после фазового сдвига с координатой z ₁)

ф ( z ) = 0, если 0 <  z <  z i

ф( z) = Аф, если zi < z < z2

как показано на рис. 2.

Распространение таких волн может быть описано связанными дифференциальными уравнениями dA_i / dz и dB_i / dz . В результате ряда преобразований для Аф = п получим

T ( X ) = у ⁴ / ( Ар ² [ Ар ² cos h ² ( у L ) +

+ у ² sin h ² ( у L ) - 2 к ² cos h ( y L ) + к ⁴ ]),

где коэффициент связи к = пА n n / X ( п — коэффициент локализации мод); 2 АР = в - п / X — па-

Ai(0)^	Ai(zi)	Аг(г1)	A2(z2)
Bi(0)	Bi(zi)	B2(zi)

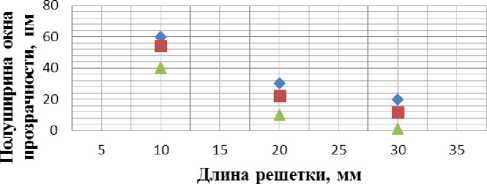
—♦—0,0001 -В-0,0002 -*—0,0005

Рис. 3. Зависимость ширины окна прозрачности решетки на полувысоте от ее длины и глубины коэффициента модуляции

0               Zi              Z2

Рис. 2. Распространение встречных волн в ВБР с фазовым сдвигом

раметр расстройки, который представляет собой разность между постоянными распространения в = 2 п n co / X и волновым числом решетки K = 2 п / Л , у ² = к ² - Ар ² , L — длина решетки.

На рис. 3 показана зависимость, полученной ширины окна прозрачности на полувысоте в зависимости от коэффициента модуляции. Из анализа рис. 3 видно, что возможно получение как сверхузких окон прозрачности, так и достаточно широких, способных регистрировать изменения температуры в пределах 5-10 ° C, при чувствительности решеток от 1 до 10 пм на 1 ° C, что вполне достаточно для построения систем автоматического регулирования.

При равномерном растяжении/сжатии ВБР с фазовым п -сдвигом соответствуют по характеристическому отклику классическим ВБР [1].

ВБР с фазовым п -сдвигом в случае приложенных к ней изгибных сил могут быть численно описаны комплексным методом, основанным на методах связанных мод и матриц передачи, которые известны как точные и эффективные методы численного моделирования.

Характеристики ВБР описываются произведением матриц 2 х 2 каждого однородного элемента решетки, что позволяет в итоге получить полную матрицу передачи ВБР. ВБР разбивается на N однородных секций, для которых определяются коэффициенты отражения R_i и пропускания S_i как амплитуды распространяющихся вперед и назад мод после прохождения i -ой секции с учетом законов фазовой и амплитудной модуляции.

После определения матриц для каждой секции можно записать

F n

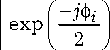
f jф, ) exp I I

где ф j = n .

Начальные условия для матрицы передачи определим как:

R (-1 /2)

S (-1 /2)

R (1 /2)S (1 /2)

RN

SN

R 0

S 0

RN1 = f f R Sn J    I So

F = F n ' F n - 1 '- F i + 1 ' F •-• F-               (6)

Для обеспечения фазового п -сдвига введем матрицу F _n между матрицами F ₊ 1 и F в (6), которая определяется как

а коэффициенты отражения и пропускания как R = S ( - 1 /2 ) / R ( - 1 / 2)| ² = |F 21 / F 11² ,        (9)

T = 1/ R ( - 1 /2 )| ² = 1/ F_n 2 .                (10)

Проведенные по методике [13] исследования показали, что провал в ВБР, вызванный фазовым сдвигом, уширяется с сохранением градиента крутизны общего уширения ВБР. Использовался пакет прикладных программ Optigrating 4.2. На рис. 4 показана спектрал ь н а я характеристика ВБР до (А) и при (Б) воздействии. При отсутствии воздействия ширина провала составляла 0,01 нм, при к = 5 м ¹ ~ 0,16 нм.

Таким образом, если для измерения ширины решетки необходимо использовать сложное спектральное оборудование, то для измерения ширины провала может быть использована методика маломодового четырехчастотного зондирования без перестройки частоты лазера с двумя неравными разностными частотами [6]. Процедура определения резонансной длины волны ВБР, ее высоты и ширины окна прозрачности на полувысоте, предложенная нами, получила название «метод вариации разностной частоты» и подробно описана в [16–18]. Исходя из ширины провала, разностные частоты должны лежать в диапазоне 1-10 ГГц для работы в диапазоне к от 0 до 5 м ^{- 1} .

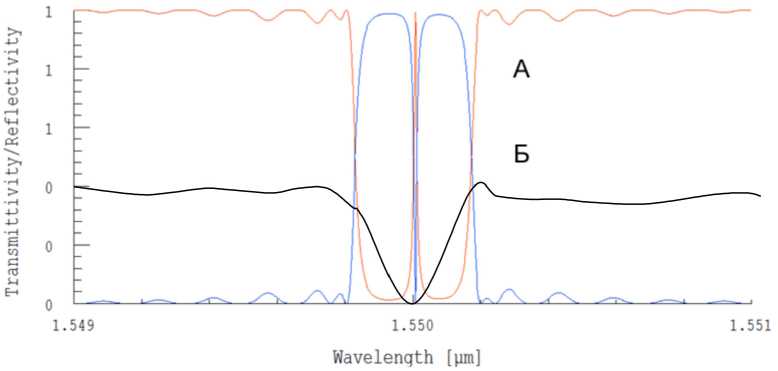
Рис. 4. Спектральная структура ВБР с фазовым п - сдвигом и ширина окна прозрачности до (А) и при (Б) воздействии

2. Периодические структуры с фазовым сдвигом в СВЧ диапазоне

Изменением конфигурации и взаимного расположения неоднородностей в БСКК возможно управление характером частотной зависимости коэффициента передачи и отражения структуры. Брэгговская структура с фазовым п -сдви-гом, реализованная в коаксиальном кабеле, характеризуется наличием участка с расстоянием между соседними неоднородностями, равным к Л / 2, где к — нечетное целое число, Л — период брэгговской структуры (расстояние между периодическими неоднородностями). Для случая к = 1 конфигурация коаксиального кабеля, где в качестве неоднородностей выступают отверстия, показана на рис. 5, а . Используя метод ориентированных графов можно получить аналитическую зависимость коэффициента отражения для брэгговской структуры с фазовым сдвигом. Ориентированный граф для случая, когда фазовый сдвиг находится в середине кабеля, будет иметь форму, показанную на рис. 5, б .

Граф представляется каскадным соединением двух одинаковых БСКК с комплексным коэффициентом отражения Г и коэффициентом передачи K и расстоянием между ними L . Выходной порт БСКК подключен к нагрузке с коэффициентом отражения Г l и отстоящей от торцевой неоднородности на расстояние Л . Общий коэффициент отражения структуры, определяемый уравнением Мейсона можно записать в виде

ГБСКК = - = Ге2jвЛ + [ K2е-2jв(L+Л) х a L х (Г - ГLe-2jрЛ(Г - K2))] / [1 - Ге-2jрЛ х (11) х (Г + ГL) - ГГLe-2je(L+Л)(K2 + Г2ГL)].

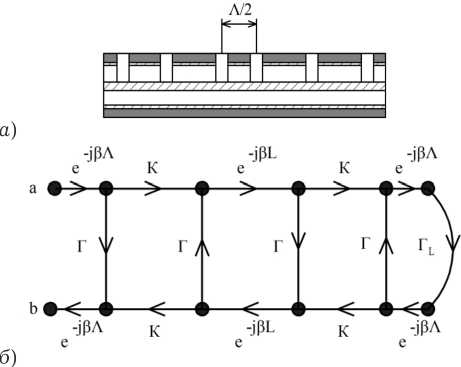
Рис. 5. Брэгговская структура в коаксиальном кабеле с фазовым п -сдвигом ( а ) и ее ориентированный граф ( б )

Коэффициенты отражения Г и передачи K без учета контуров более чем второго порядка, передача которых содержит коэффициент отражения единичной неоднородности Г н в четвертой и более степенях, выглядят как

Г =

-

N

г н £ (1 + Г н ) ²⁽ i ^{- 1)} e ^{- 2}ji (1

i = 1

-

Г H ² £ ( N - к - i + 1)(1 + Г H ) ^{2( к - 1)} e ^{- 2 jk вЛ} ) к = 1

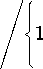
N

-Г H ² £ ( N - i )(1 + Г H ) ²⁽ i ^{- 1)} e ^{- 2 ji вЛ} i = 1

(1 + Г H ) Ne - j ⁽ N ^{+ 1) вЛ}

1 -Г H ² £ ( N - i )(1 + Г H ) ²⁽ i ^{- 1)} e^{-2 ji вЛ} i = 1

Анализ частотной характеристики коэффициента отражения БСКК осуществлялся для различных значений фазового сдвига и расположе-

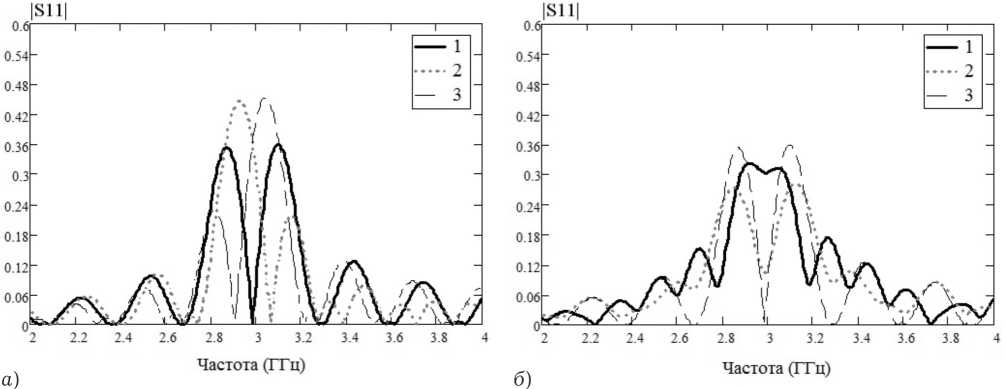
Рис. 6. Частотная характеристика коэффициента отражения БССКК: а ) для различных фазовых сдвигов (1 – π , 2 – π /2, 3 – 3 π /2), б ) для различных мест расположения фазового π - сдвига от конца кабеля (1 – 0,2 длины кабеля, 2 – 0,3 длины кабеля, 3 – 0,5 длины кабеля)

ния секции сдвига фаз по длине кабеля. Рис. 6, а показывает характер резонансной кривой при изменении расстояния между центральными неоднородностями для трех значений фазового сдвига – π , π /2 и 3 π /2. Рис. 6, б показывает характер резонансной кривой при изменении местоположения секции с фазовым π -сдвигом для трех вариантов расположения: в центре кабеля, на расстоянии от конца кабеля 0,2 и 0,3 от общей длины кабеля.

Известны приложения брэгговских СВЧ-структур в коаксиальном кабеле в задачах определения диэлектрических характеристик жидких сред [2]. Метод основан на внесении исследуемой жидкости в ячейки структуры, образованные периодическими отверстиями во внешнем проводнике и диэлектрике кабеля. Изменение эффективной диэлектрической проницаемости неоднородности приводит к преобразованию формы характеристики, из которой может быть извлечена информация об исходных свойствах жидкой среды. Устройства контроля на основе БССКК могут быть использованы в различных автоматизированных технологических процессах. Структура с эквидистантным расположением неоднородностей имеет некоторые недостатки использования в качестве сенсоров диэлектрических параметров, одним из которых является невысокая чувствительность.

Повысить чувствительность измерительной системы может позволить конфигурация БССКК с фазовым π-сдвигом. За счет высокой добротности контура определение смещения резонансной частоты в зависимости от диэлектрических свойств жидкости осуществляется с большей точностью нежели в случае с эквидистантной периодической структурой.

Проведен вычислительный эксперимент по определению частотной зависимости коэффициента отражения БССКК с фазовым π -сдвигом при различных значениях комплексной диэлектрической проницаемости введенной в ячейки среды. Расчет производился методом графов с предварительным получением матрицы рассеяния неоднородного участка в виде сегмента коаксиального кабеля с введенной в отверстие исследуемой жидкостью в программе электромагнитного моделирования Microwave CST S t udio. Значения диэлектрической проницаемости ε лежали в диапазоне: от 3 до 20, тангенса угла диэлектрических потерь tg δ в диапазоне от 0.1 до 0.9. На рис. 1, а показан коэффициент отражения структуры с 10 отверстиями для среды с tg δ= 0.1 при различных значениях ε , на рис. 1, б – для tg δ = 0.9.

Анализируя полученные зависимости можно наблюдать, что зависимость центральной частоты узкого резонанса от значения ε носит линейный характер, а зависимость амплитуды резонанса от ε имеет вид y ( x ) = 1/ (1 + exp( - kx )). При этом четкость определения резонанса ухудшается при больших значениях ε и tg δ .

Уменьшая количество отверстий в структуре можно несколько исправить данный недостаток, но подобный влечет за собой увеличение полосы резонансной характеристики, поэтому для улучшения измерительных показателей необходим поиск других решений. Одним из таких подходов является уменьшение эффективной диэлектрической проницаемости неоднородного

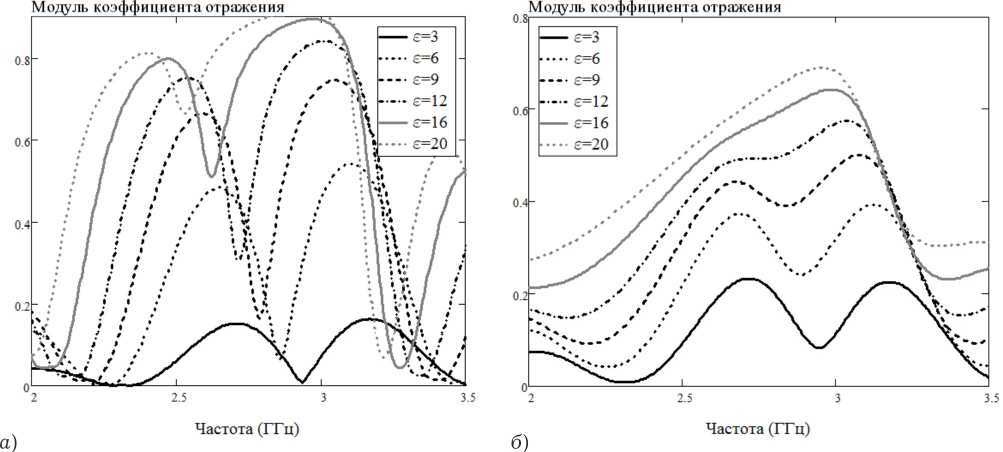
Рис. 7. Частотные зависимости коэффициента отражения БСКК с фазовым π - сдвигом при заполнении ячеек

участка для случая высоких значений ε и tg δ исследуемой среды, что обеспечивается уменьшением глубины отверстия в коаксиальном кабеле.

Рис. 7 иллюстрирует результат уменьшения глубины ячейки на 0,25 от максимального значения, где можно наблюдать достигнутое расширение диапазона контролируемых параметров ε и tg δ .

Заключение

Показана эффективность использования сложно-периодических структур оптического и радиочастотного диапазонов для повышения метрологических характеристик датчиков физических полей и контроля параметров материалов. По результатам анализа температурных, барических и изгибных эффектов ВБР с фазовым π -сдвигом, рассмотренным в настоящей статье, будут определены структуры датчиков для измерения температуры, линейного и изгибного натяжения с применением в волоконно-оптических сенсорных системах. Использование ВБР с фазовым π -сдвигом позволит повысить разрешающую способность проводимых измерений в 10–50 раз, чувствительность – в 1,7–3,2 раза по сравнению с гомодинными методами измерений, использующими классические ВБР. БСКК с фазовым π -сдвигом позволяют получить в 5–7 раз большую чувствительность измерителей электрофизических параметров сред по сравнению с аналогичными эквидистантными структурами.

Работа выполнена при финансовой поддержке Министерства образования и науки Российс^

кой Федерации в рамках проектной части Го^ сударственного Задания З.1962.2014/К.