Свойства спутной оболочки, образующейся в мезосфере вокруг ЛА при гиперзвуковом движении

Перед спускаемым аппаратом (СА) образуется ударная волна (УВ). Происходят ионизация газа и его снос по потоку, и, как следствие, возникает проблема с организацией радиообмена. Существуют также вопросы и для радиолокации. Рабочая частота ю при этом должна превышать критическую частоту ω₀, которая равняется электронной плазменной частоте ω _p = 2πν _p для плазменного состояния. Если частота столкновений электронов ν _е превышает расчетное значение плазменной частоты ν _p , то ионизованный газ не достигает плазменного состояния, но существенно ослабляет радиосигнал. Эти задачи возникают и на активном участке траектории вывода космического аппарата (КА). Так, значительную часть времени КА многоразового использования находится в мезосфере Земли (40...45 – 85…90 км), развивая при этом суперзвуковую скорость. Актуальность задачи возрастает в связи с развитием космического туризма.

1. Образование оболочки

В скачке уплотнения УВ происходят нагрев газа, диссоциация и, наконец, ионизация. Известно, что керамическая защита антенны СА разогревается до 3000 К. Газ же достигает температуры 10⁴ К. На рис. 1 пре д ставлен результат компьютерного моделирования [1]. СА малого размера окутываются плазмой практически полностью. У крупных объектов с обратной сто-

роны относительно направления вектора движения остается окно радиопрозрачности.

На рис. 2 показаны расчетные зависимости электронной плотности n_e от скорости СА v при торможении на различных высотах [2]. Плотность n_e возрастает с уменьшением высоты, но скорость v уменьшается. На высоте h = 75 км при скорости v = 5 км/с плотность n_e ≈ 10¹⁸ м ^{- 3} при частоте столкновений ν _e ≈ 10¹¹ Гц, что наблюдается и на высоте h = 100 км.

На рис. 3 в качестве примера представлена схема температурного нагружения поверхности «Бурана» [3]. Максимальная температура в носо-

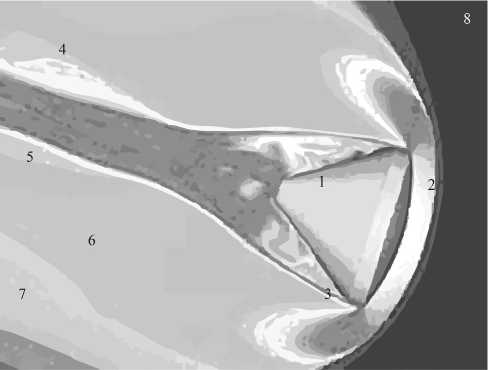
Рис. 1. Торможение СА: 1 – космическая капсула; 2 – область УВ с температурой 6000 К и выше; 3 – спутный поток с температурой 5000 К; 4 – след, 4000 К; 5 – след, 3000 К; 6 – область перемешивания, 2000 К; 7 – то же, 1000 К; 8 – невозмущенное пространство

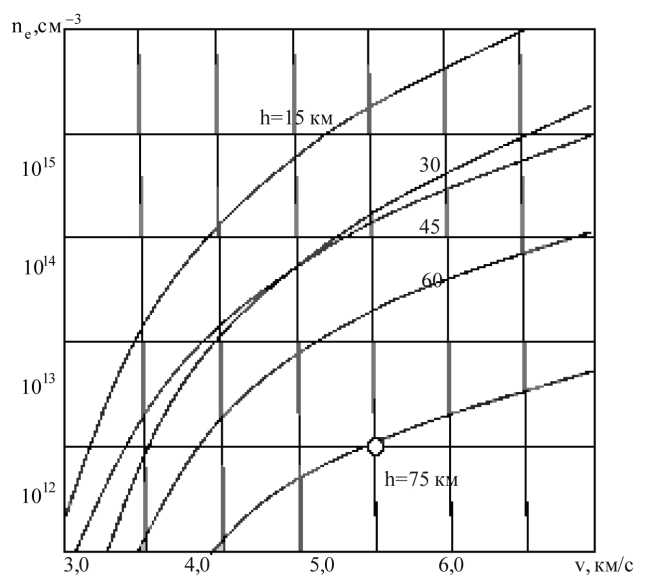
Рис. 2. Плотность электронов n_e в области прямого скачка уплотнения в зависимости от скорости движения v при торможении СА

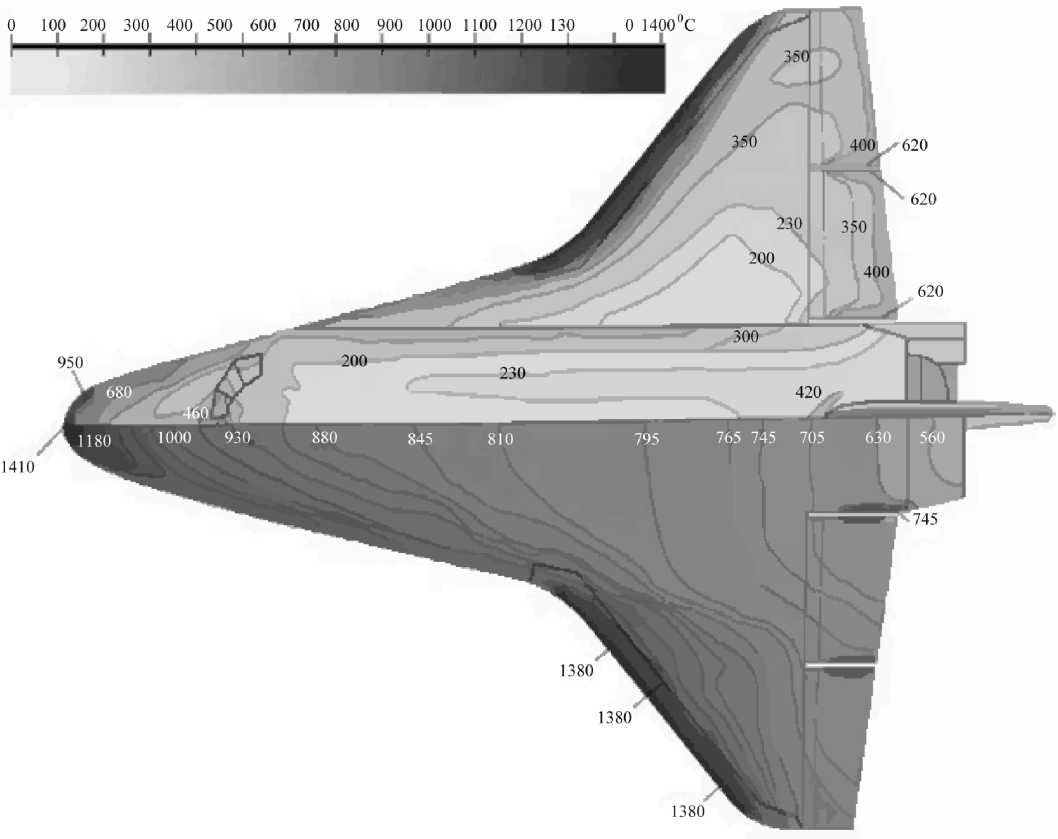
Рис. 3. Уровни внешнего нагрева корпуса «Бурана»: h = 63 км, М = 17

Рис. 4. Ударные волны в сверхзвуковой аэродинамической трубе, образующиеся при обтекании модели летательного аппарата

вой части 1410 °C. Разогрев газов осуществляется за счет ударной волны. Температурное поле оболочки с учетом 10 % коэффициента тепло-переноса вблизи поверхности на порядок выше (точными данными авторы не располагают).

2. Исследуемая среда

При обтекании сверхзвуковым газовым потоком твердого тела на его передней кромке образуется ударная волна (иногда и не одна, в зависимости от формы тела). На рис. 4 видны ударные волны, образованные на острие фюзеляжа модели, на передней и задней кромках крыла и на заднем окончании модели [3].

На фронте ударной волны скачкообразно происходят кардинальные изменения свойств пото- ка – его скорость относительно тела снижается и становится дозвуковой, давление в потоке и температура газа скачком возрастают. Толщина фронта ударной волны имеет порядок длин свободного пробега молекул, что позволяет в расчетах фронт заменить поверхностью разрыва [4]. За фронтом газ образует по направлению Z сло- истую структуру, и внутри слоев газ можно считать однородным. Так называемая адиабата Гюгонио идет круче, чем дозвуковая адиабата. Для гиперзвуковых УВ (число Маха М = v / a превышает 6) для плотности р получается:

р1 = (цД

Ро    (Y - 1) .

Здесь у — показатель классической адиабаты. Индекс «0» соответствует невозмущенной части, «1» – сжатму состоянию.

Предельное сжатие для одноатомного газа равно 4 (три степени свободы), а для двухатомного – 6 (пять степеней свободы). Оставшаяся при относительном торможении энергия идет на нагрев газа, диссоциацию, ионизацию.

Обратимся к электронной компоненте ионизованного газа, которая определяет радиофизические свойства исследуемой среды. Степень ионизации определяется скоростями прямых и обратных процессов. Условие равновесия ионизации при электронном ударе и рекомбинации при тройных столкновениях имеет вид k1 nane = knin2, где na, ni и ne — концентрации атомов, ионов и электронов; k1 и k2 – константы скоростей процессов. Концентрация заряженных частиц определяется формулой Саха. Такими же соотношениями определяется равновесие при термической ионизации – происходят идентич- ные процессы.

Запишем формулу Саха для концентрации электронов n_e [4]:

n e = ( 2n m e ) ^0.7 5 ( k b T )^0.2 5 P ₀ ^0. 5 h "^L5 exp

), (2)

2 kT J

где m e — масса электрона; x _r — энергия ионизации; h – постоянная Планка; T – кинетическая температура, P ₀ – давление нейтрального газа; k_b – постоянная Больцмана. В смеси газов рассматривается легкоионизируемая компонента, концентрация которой n ₀. Естественно, что n e <  n 0 . Но если не хватает легкоионизируемой компоненты, то пополнение электронной концентрации происходит за счет следующей по степени ионизации компоненты.

Столкновительный ионизованный газ (СИГ) – это трехкомпонентная среда электронов, ионов и атомов (молекул) с относительно малой степенью ионизации. Радиус Дебая – Гюккеля – 5 характеризует масштаб квазинейтральности или электрической неоднородности СИГ (здесь и далее предполагается, что параметры приводятся в усредненном виде). Кулоновское взаимодействие частиц мало в сравнении с kT при выполнении неравенства

e kT

"T” s <     ,

4лб о О     e

где S o — электрическая постоянная.

Основными характеристиками СИГ также яв-

ляются v _e — частота столкновений электронов и

to p — плазменная частота [5]:

В переходной области применимы комплексные характеристики. Комплексная проницаемость S в мнимой части содержит проводимость S = S — i ст / ( s q to ) , что связано с наличием «потерь». Представим проводимость в комплексной форме: ст = ст r — i ст i . Рассмотрим материальное уравнение для плотности тока: j = ст E , где j = en e u . Запишем уравнение движения (5) в комплексной форме для электронов, имеющих скорость u ( t ) = U exp ( i to t ):

u v e = e ; to p К

₂ 0.5 n e e

(^S 0 m e J

me

du ( t ) dt

= i to m_eu ( t ) = - e E - v _em_eu ( t ).

Плазменные колебания могут развиваться и существовать на т _e - интервале между двумя столкновениями: т _e = 1/ v _e . Характерные параметры для ионизованного газа и газовой плазмы: to p т _e > 1, 5 ^ L , N g » 1 — газовая плазма;

to p т e < 1, 5 « L , т m = S o / ст, N g » 1 — ионизованный газ.                          (4)

Из материального уравнения и уравнения движения получаем действительную — ст r и мнимую — ст i компоненты комплексной прово-

димости:

e n_e    v _e _   _ _e n e    to

”   27  2^{; c} i =        2~  2 .

m e v e + to            m e v e + to

Здесь L – линейный масштаб исследуемой среды; N g — количество заряженных частиц в сфере Дебая; т м — максвелловское время установления квазинейтральности (для СИГ связано с v _e ); ст — коэффициент электропроводности. При малом N g газ становится слабоионизиро-ванным, и тепловое движение «маскирует» действие кулоновских сил. При 2nv _e > to p электроны сталкиваются с частицами газа столь часто, что

3. Радиофизические свойства среды СИГ

Итак, рассмотрим два принципиально различных состояния СИГ – плазменное и не плазменное. Для фазовой функции — в и функции затухания — а известны частотные зависимости [6]:

в² = 2/ to ₂Л

2 - 2 (v e + to²)

характер их движения определяется газодина-

X

'² + to² - to²)² + v 2 to 4 + to(v 2 + to² epepe

-

(8) ^to p ) ) ,

мическими, а не электрическими силами.

Характер поведения электронов в целом определяется дифференциальным уравнением движения (относительно координаты z ):

2 = ^to _X

2 c 2 (v e + to²)

x (^²(v e +to² - to p ) 2 +v 2 to p - to(v 2 +to²

me

d ² z_e dt

^{- to} p ) ) .

- eE z

+ v e m e

d ( Z o - Z e ) dt

+

e ne

^S o

( z_o

- z e )■

Последнее слагаемое определяет наведенное поле за счет динамического воздействия со стороны нейтральной компоненты при ее движении. Если исключить влияние внешнего поля E и массовое движения газа, то, естественно, получается плазменная частота to p .

В рамках феноменологического подхода радиофизические свойства СИГ описываются «материальными уравнениями среды». Диэлектрические свойства среды характеризуются относительной диэлектрической проницаемостью s(to), а проводящие свойства — проводимостью c(to).

А. Не плазменное состояние столкновительно-го ионизованного газа – собственно СИГ при 2nv _e > to p (здесь to p — расчетный параметр). На толщине скин-слоя 5 поглощение происходит практически без отражения. Заметим, что диапазон перехода к радиопрозрачности здесь четко не определен.

В правых частях уравнений (8) и (9) введем безразмерные частоты относительно v _e :

to               top v =----и v = ——.                  (10)

^r 2nv_e     ^rp 2nv _e

В левых частях (8) и (9) введем безразмерную форму записи:

P 2 i =в²   и a A = a² —.                   (11)

v 2 _e               v 2 _e

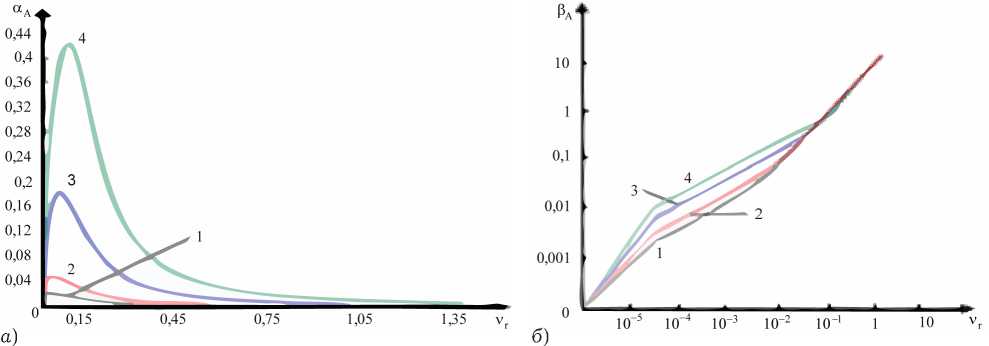
Рис. 5. Зависимости функций затухания в СИГ от относительной частоты ( а ); зависимости фазовых функций в СИГ от относительной частоты ( б )

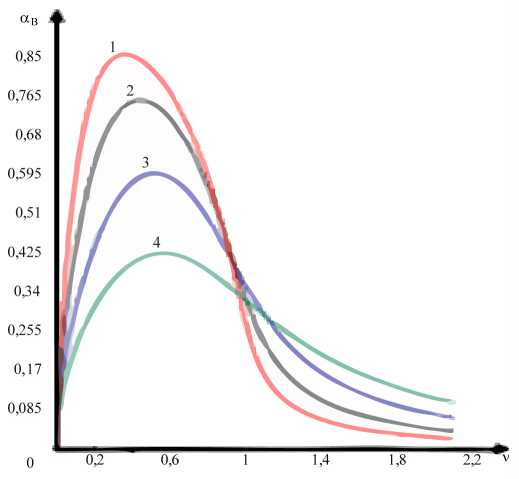
а )

Рис. 6. Зависимости функций затухания в СГП от относительной частоты ( а ); зависимости фазовых функций в СГП от относительной частоты ( б )

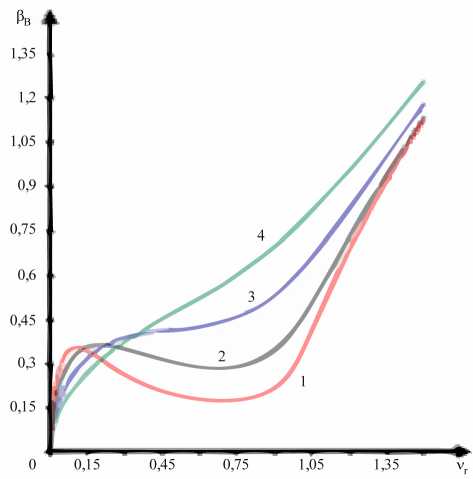
б )

После выполнения подстановок получаем:

2 _     2n²v r

Р A =

о(1 + 4п v r )

х (^ю2(1 + 4n2(vr - vrp))2 + 16n4vrpv2 +

+ о(1 + 4n (v r — v rp )) ) .

22n aA =21“

о(1 + 4n v r )

х (^02(1 + 4n2(vr — vrp ))2 + 16n4vrpv2 —

• — to(1 + 4n (vr — vrp))) .

Модельные зависимости для СИГ пред- ставлены на рис. 5, а и на рис. 5, б для слу- чаев: 1) vrp = 1/ 30; 2) vrp = 1/ 20; 3) vrp = 1/10;

• 4) v rp = 1/ 2п. Анализ представленных здесь частотных зависимостей (рис. 5) показывает, что действительно для СИГ необходимо доопределить значение частоты или частотный диапазон перехода к радиопрозрачности (см. А). Однако на фазовых частотных зависимостях можно отметить особую частотную область, где они сливаются в линию одинакового наклона. Окончательно это происходит при единичной относительной частоте.

В. Плазменное состояние столкновительно-го ионизованного газа — СГП, если 2nv e < to p . Среда становится радиопрозрачной при частоте, превышающей to p . Отражение наблюдается на частоте о ниже to p , но при to > 2nv e .

В правых частях уравнений (8) и (9) введем относительные частоты:

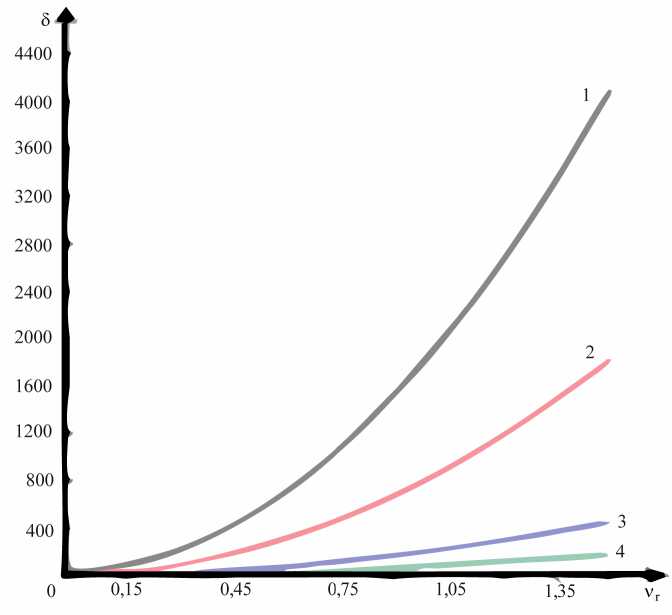
Рис. 7. Зависимости глубины скин-слоя от частоты ν _r для СИГ

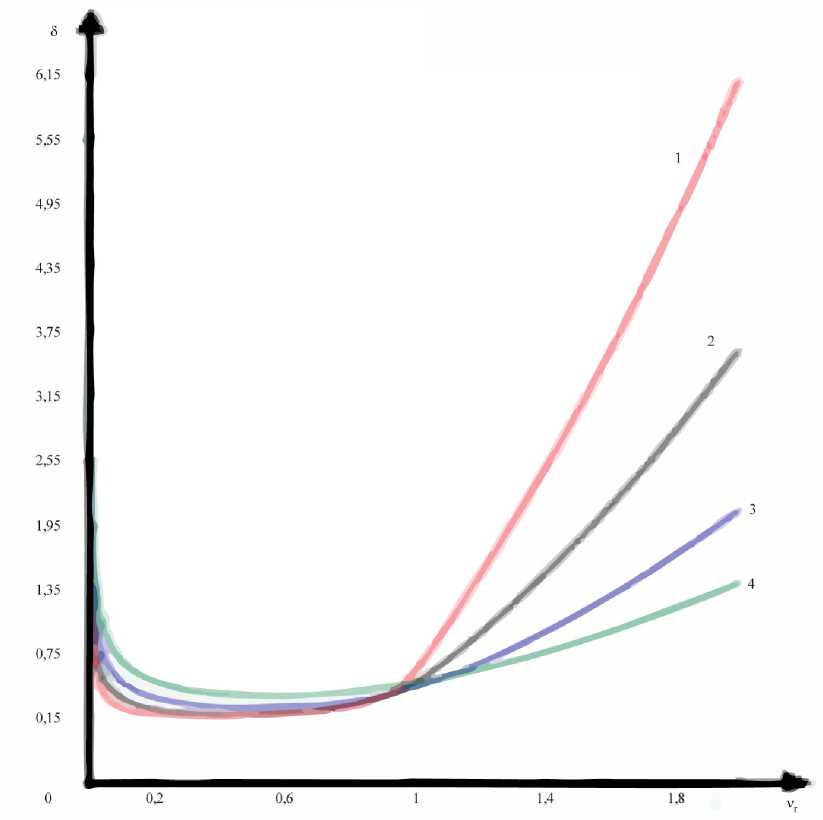
Рис. 8. Зависимости глубины скин-слоя от частоты νr для СГП to vr = и vre top ve top

.

« В =

vr

2( v ² e + v Г )

х

х

( 2/2.2        2.2            /2.2

д/ v r ( v_re + v r — 1) + v_re - v r ( v_re + v r

- ¹⁾ ) •

e B =     2 vr 2 х

2( v ; _e + v 2 )

х

( ^v 2 (v²_ee + v ² - 1)² + v 2 _e + v r ( v 2 _e + v 2 - 1) ) ,

где вв = ₽2 -2 и аВ = а2 -2 .                  (17)

^to p                ^to p

Анализ представленных здесь частотных функций (рис. 6) показывает, что действительно значение частоты перехода к радиопрозрачности для СГП определяется выражением to > 2nv _e (см. В), что со о тветствует относительной частоте v r = to / to p , равной 1. Для анализа изменения глубины проникновения электромагнитной волны в среду воспользуемся обратной зависимостью от функции затухания – здесь это касается выражения (15). Для СГП с параметрами: 1) v _re = 1 /V30, 2) 1 /710, 3) 1/ Т3, 4) 1, частотные зависимости для 5 представлены на рис. 6. Переход к радиопрозрачности действительно наступает при относительной частоте, равной единице, и тем резче, чем меньше частота столкновений. На низких частотах (меньше 0,5 относительной частоты) функции затухания уменьшаются, т. к. длины волн превышают значения скин-слоя и условие модельности нарушается.

Заключение

Для анализа изменения глубины проникновения электромагнитной волны в исследуемые среды воспользуемся определением зависимости глубины скин-слоя 5 от частоты как обратной зависимости от функции затухания [5] – здесь это касается выражений (13), (16). Для СИГ с исследуемыми параметрами (см. А) частотные зависимости для 5 представлены на рис. 7; для СГП (см. В) – рис. 8.

Анализируя зависимости, изображенные на рис. 7 и 8, необходимо отметить следующее.

• 1)    Физический смысл величины относительного скин-слоя для СИГ состоит в отражении количества длин волн электрон-атомных столкновений, на котором произойдет затухание сигнала (следует из (10))

• 2)    Физический смысл величины относительного скин-слоя для СГП состоит в отражении количества длин волн плазменных колебаний, деленных на 2п, на котором произойдет затухание сигнала (следует из (14)).

• 3)    Цена деления оси абсцисс на рис. 7 получается в 2п раз больше в абсолютных величинах, чем для рис. 8 (в силу соотношений (10) и (14)).

• 4)    Для оценки корректности полученных модельных зависимостей для СИГ и СГП введен предельный случай (обозначен 4 на всех графиках) (т. е. когда среда является и СИГ, и СГП одновременно). Соответствие очевидно.

Для СИГ наступает прозрачность радиоволн при превышении частоты электрон-атомных столкновений (в 1,5–2 раза). Для СГП прозрачность наступает с превышением частоты радиоволн значения плазменной частоты. При этом выполняется линейность зависимости фазовой функции и стремится к нулю частотная функция затухания. Критическая частота достигает значения 10 ГГц на высоте 70 км [5; 7].

Переход от безразмерных к абсолютным параметрам не требует каких-либо дополнительных математических преобразований и сводится лишь к умножению. Для нахождения оптимальной частоты, зная параметры среды (v _e , to p ) и толщину плазменного слоя, необходимо потребовать, чтобы последняя была меньше расчетной величины скин-слоя.