Symptomatic and Climatic Based Malaria Threat Detection Using Multilevel Thresholding Feed-Forward Neural Network

Published Online August 2017 in MECS

• I.    Introduction

  Several diseases affects the proper functioning of human‘s health and poor health condition affects one’s life span and achievements. One of such common disease is malaria. According to World Health Organization (WHO) Report in 2015, there are 95 countries and territories with ongoing malaria transmission, and only 6 countries have eliminated malaria(WHO,2015). Globally, an estimated 3.4 billion people are at risk of malaria. WHO estimates that 214 million new cases of malaria occurred globally in 2015 (range 149 -303 million) and an estimated death of 438,000, 000. Most cases (88%) and deaths (90%) occurred in Africa , and most deaths (71%) were in children under 5 years of age (WHO, 2014). WHO has made malaria reduction a chief priority. The idea is to disable the disease by combining virtually every known malaria-fighting technique. Bill Gates, who has called malaria “the worst thing on the planet,” has donated hundreds of millions of dollars to the effort through the Bill and Melinda Gates Foundation. The Bush Administration has pledged 1.2 billion dollars (WHO, 2015). Funds devoted to malaria have doubled since 2003. The idea is to disable the disease by combining virtually every known malaria-fighting technique, from the ancient (Chinese herbal medicines) to the old (bed nets) to the ultramodern (multidrug cocktails). But, the rate at which malaria prevails in the concerned areas seems exponential despite thefact that all hands are on desk to combat the spread and even eradicate the disease (Owoseni and Ogundahunsi, 2016). At the same time, malaria researchers are pursuing a long-sought, elusive goal: a vaccine and methods that would curb the disease for good (WHO, 2014;2015).

Malaria transmission is site specific due to different climatic change of a region. There are three main climatic factors that directly affect malaria transmission. They are temperature, rainfall and relative humidity (Depinay et al , 2004). Several non-climatic factors, such as human or behavioural factors can also affect the pattern of malaria transmission and the severity of the problem. Malaria parasite develops more quickly at higher temperatures. Higher temperatures increase the number of blood meals taken and the number of eggs laid by the mosquitoes, which increases the number of mosquitoes in a given area. The minimum temperature for mosquito development is between 8–10°C; the optimum temperature is 25–27°C, and the maximum temperature is 40°C. Altitude influences the distribution and transmission of malaria indirectly, through its effect on temperature. As altitude increases, temperature decreases, so highlands are colder and lowlands are warmer.

Data mining has great potential for the healthcare systems to use medical data for analysis and to offer improved healthcare at reduced cost. These in health care play a significant role in prediction and diagnosis of various health problems like heart disease, diabetes, malaria, cancer, skin disease and many more(Shetty and Joshi, 2016). Recent researches world widely is focusing on the new applications in the medical field and particularly in diagnosis (Depinay et al 2004).

The healthcare sector is showing inclination towards restructuring of healthcare systems to harmonize with technological innovations and adopting decision support system in routine clinical practices(Alqahtani et al, 2016). Medical experts are now demanding for knowledge intensive Computational Intelligence (CI) and Knowledge Based System(KBS) in finding solutions to medical problems (Adetumbi, Oguntimilehin and Falaki, 2012).

Dynamics of Malaria parasite transmission is complex and been widely studied. Research is needed to understand how the risk of asymptomatic and symptomatic malaria infection changes. Diagnosing asymptomatic malaria transmission is not straightforward due to the obvious lack of clinical manifestations and often sub-patient levels of parasites are undetectable by microscopy (Bottius et al., 1996). The extent of the prevalence of asymptomatic parasitemia in a given population is inversely related to the population’s susceptibility to clinical disease (Bereczky et al . 2007, Mwangi et al., 2008). Asymptomatic malaria infection cases are prevalent in malaria endemic regions and have become a serious cause for concern as efforts are increasing towards eliminating the parasite (Trape, Zoulani & Quinet, (1987).

Consequently, most existing conventional malaria models for classification problems examine the dynamics of asymptomatic and morphological characteristics of malaria parasite. Malaria diagnosis may be asymptomatically or symptomatically low, mild and high. Many symptoms of different patient may even overlap. A malaria patient may even have characteristics of other diseases. Medical problems, therefore, cannot be generalized and analyzed using imagination. An analytical program is desperately required to integrate this complex network of problems and devise individualized solutions (Onuwa, 2014). The need to predict the multiclass symptomatic characteristics of malaria parasite combined with effects of climatic factor which is a great great determinant of malaria severity is of great importance. A huge amount of malaria incidences are captured every year and there are difficulties in predicting its future occurrence and analysis of its possible threats. So the need for a machine learning method arises. Such a machine processes the data and automatically finds structures in the data, i.e. learns. The knowledge about the extracted structure can be used to solve the problem at hand.

• II.    Statement of the Problem

  Malaria is still a major public health problem as 109 countries are declared endemic to the diseases (Hay, Gething & Snow, 2010). Virtually all humans are being diagnosed of malaria infections at one time or the other especially in tropical area in Africa and its negative effects increases drastically and cause great harm to human life (Mendis, Sina, Marchesini & Carter (2001). The presence of both symptomatic and asymptomatic diagnostic measure is very vital in detecting the transmission dynamics of malaria infection. To avoid the occurrence of new malaria outbreaks in both endemic and non endemic areas, an improve methods are needed to decrease the parasite sources of infection by active search and treatment of symptomatic and asymptomatic parasite carriers. The aim of this paper is to explore threats and factors that contributes to having malaria and developed Malaria Symptomatic Predicting model to diagnose the severity of malaria parasite.

• III.    Choice of Predicting Model

  Conceptualized, data mining and knowledge discovery on the unstructured data is needed to be carried out(Goswami and Chakrabarti, 2014). But the choice of machine learning algorithm to solve a problem always depends on the size, quality, and nature of the data (Djam et al., 2011).

Table 1. Strength and Weaknesses of Various CI tools

Characteristics Model	FL	ANN	SVM	GA
Function Approximate Reasoning	Mild	High	High	High
Learning Abilities	Low	High	High	High
Handling of Uncertainties	High	High	High	High
Fault Tolerance	Low	High	High	High
Massive Parallelism	Low	High	High	High
Capability to solve Multiclass Problem	Low	High	Low	Mild
Threshold Metrics(accuracy)	Mild	High	High	Mild
Probability Metrics(MSE)	Low	Low	Low	Low
Rank Metrics(ROC)	Low	High	Mild	Mild
Training Time	High	Low	Low	High
Number of Features	Low	High	Mild	High
Number of Training Data	Low	Mild	Mild	Mild

Sources: [Sharma, V., Rai, S., & Dev, A.(2012); Castillo et al., 2001a,b). Karnik and

To produce powerful computing systems, artificial intelligence technologies have a natural effectiveness that can be exploited (Niksaz and Mohammad , 2014).

In this study after consideration of strength and weaknesses of various Computational/Artificial Intelligence (CI) Tools; Fuzzy Logic(FL), Artificial Neural Network(ANN), Support Vector machine(SVM) and Genetic Algorithm(GA), shown in Table 1above is based on the nature, size and quality of the data. The choice of ANN having underlining Feed-Forward Neural Network (FFN) and Back Propagation algo (BPa) was made.

• IV.    Feed- Forward Neural Network(Ffn) and Back Propagation Algorithm(Bpa) Model

A network of perceptrons with a differentiable squashing function, usually the sigmoid (logsig) function is called feed-forward neural network. The back propagation algorithm (BPa) adjusts the weights based on the idea of minimizing the squared error. The differentiable squashing function of feed-forward neural network enables the back propagation algorithm to adjust the weights across multiple hidden layers.

By having multiple nodes on each layer, the Exclusive-OR, or the XOR problem and n-separable problems can be solved by FF_BP- NN could not be solved with only the perceptron. Fig.1 shows a fully connected feedforward neural network; from input to output, each node is connected to every node on the adjacent layers. In this research, a malaria severity analysis based on feed forward-error back-propagation algorithm is proposed. The required parameters are:

• a.    Squashing Function ( S_r )

• b.   I nput vector of the network( ̅ )

• c.    Weight Vector of the network( ̅)

• d.    Neuron Activation function( Фг )

• e.    Error Function(E г )

• f.    Desired Target ( Т_т )

• g.  Weight Adjustment(Δ W )

• h.    Learning rate ( ц )

By using the log-sigmoid transfer function the Output function of this FNN Multilayer network is sr ( ̅, ̅) = 1+еФг ( ̅, ̅)                   (1)

And the error function for the output of each neuron is thus:

E г ( ̅, ̅,T) = ( S_r ( ̅, ̅) - Ту )²            (2)

We take the square of the difference between the output s_r ( ̅, ̅) and the desired target Т_г because it will be always positive, and because it will be greater if the difference is big, and lesser if the difference is small.

The error of the network will simply be the sum of the errors of all the neurons in the output layer:

E г ( ̅, ̅, ^̅) =∑ г ( s_r ( ̅, ̅) - ^т ) ²       (3)

Since, the error function for the output of each neuron in equation (1) above is :

E г ( ̅, ̅,T) = ( S_T ( ̅, ̅) - Тг ₎ 2

The back propagation algorithm now calculates how the error depends on the output, inputs, and weights by using the gradient descent method:

л              ЭЕ

∆ W_T] =- ^        (4)

Thus adjustment of each weight denoted by ∆Wrj is the negative of constant mew (ц) multiplied by derivative of the previous weight dependence on the error of the network. This means that the size of the adjustment depends on mew (ц) and contribution of the weight to the error function. The goal of backpropagation algorithm is to find the derivative of E in respect to Wrj

Firstly we need to calculate how much erro r depends on the output which is:

ар

₌₂₍ s_r ^- Tr )

Secondly, how much of the output depends on the activation function which in turn depends on the weight from equation (1) and (2)

Equation (8) above is for training with two layers.

For training with one more layer we need to adjust the y weights say Z j _k of previous layer. Firstly we will calculate how the error depends on the input from previous layer rather than on the weight. We only need to change x j in equation (6), (7), (8) above with weight Z j _k. Also we can see how the error of the network depends on the adjustment of Z jk in equation (9) and (1.9) below:

Д „           dE          dE dxj

∆ ^jk = -      = -

Where, asT _ as,. Эфт

dwrj дфг dwrj

=   (1- s_r ) Xj

₌₂₍ s_r ^- Ту ) s_r (1- s_r ) w_Tj (10)

UWyj                                 J

Then from (3.48) and (3.49) above

_{=        = 2(} s_r - Ту ) s_r (1- s_r )    (7)

О vV yj         О vV у j

So the adjustment to each weight from gradient descent function in (4) above is

Consequently, to add another layer to the network, we can calculate how the error depends on the weights and inputs of the previous layers.

Pratically, implementing back propagation algorithm in FNN should not have too many layers since the time for training grows exponentially.

∆ w_rj =-2 Ц ( S_r ^- T_r ) Sr (1- Sr ) Xj      (8)

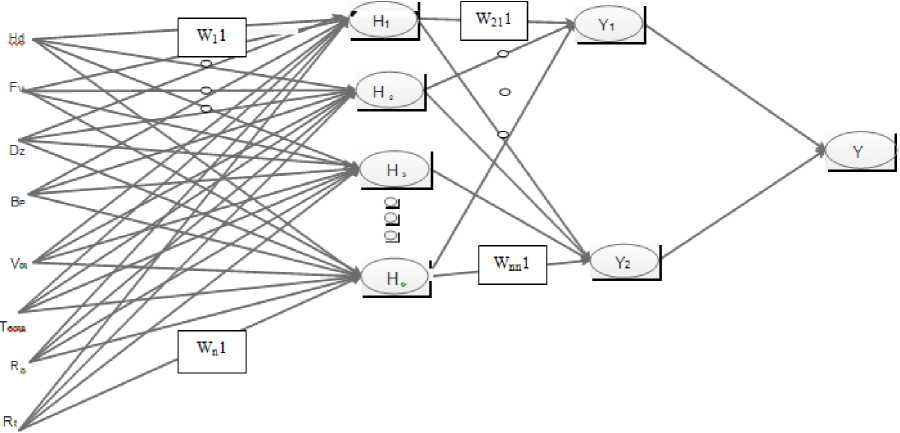
Fig.1. A fully connected Schematic Description of Malaria Feed-Forward Back-Propagation (FF_BP) Neural Network.

• V.    Binary Encoding and Normalization of Dataset Features

Given a number of features, wrapper method was used to select subset of features that have the greatest predictive power and still carry their class discriminatory properties. This research features is thus restricted to five (5) predominant malarial symptoms Headache(H d ), Fever(F v ), Dizziness(D z ), Body Pain(B p ) and Vomiting and three(3) significant climatic factors that contributes to having malaria; Temperature (T emp ), Relative humidity (R_h) and Rainfall.

Table 2. Binary Encoding Threat Classes

Malaria parasite Count Multiclass Output(class)	Malaria parasite Count Binary-class Output	Output for Qualitative Computation (OPT1	Output for Qualitative Computatio n (OPT2)
Insignificant (0)	Insignificant	0	0
{ }	(0) { }
	Significant(1		1
Significant(1) +	and above ) ≥ +	0
Highly		1	0
Significant(2)++

In this research features with missing data are assigned zero. A typical example is the rainfall data features. In order to standardize the range of independent variables or features of data feature scaling and unitary method were used and the binary encoding threat classes are represented in Table 2.

• VI.    Adaptive Static Thresholding

The Feed-Forward Back-Propagation(FF_BP) Neural Network Model was thresholded to get the optimum threshold value that will yield best result for the model using the adaptive thresholding algorithm in Table 3 below. At training section of the model the thresholding ranges from 0.4 to 1.0 to search for the optimal threshold that gives highest accuracy with low error rate and low standard deviation. At the testing stage, the thresholding algorithm gave the best trade off search of the threshold optimal parameters of accuracy, sensitivity, specificity, false negative and false positive rate.

Table 3. Adaptive Thresholding Algorithm

Input: Training Malaria Datasets

Output:  Thresholds Values, Accuracy, Mean and Standard

Deviation

• 1.    Begin

• 2.    Supply the Malaria Data Features

• 3.    Divide the data into Training Malaria Datasets and Testing Malaria Datasets in ratio 70:30

• 4.     While Threshold_Value > =0.575 Step 0.05 Do

• 5.     While Accuracy_Instances<= No_of _Runs

• 6.    Perform ANN Training

• 7.    Get Error and Performance Computation

• 8.    Simulate with Transposed Testing Malaria Datasets

• 9.    Get Simulation Results thresholding

• 10.   Get Optimun Threshold_Value

• 11.    Compute Threat rate and Classiffication Accuracy

• 12.  EndWhile

• 13.    Tabulation of Threshold_Value, Accuracy, Mean and Standard Deviation

• 14.    EndWhile Threshold_Value = 0.750

• 15.    End

• VII.    Result

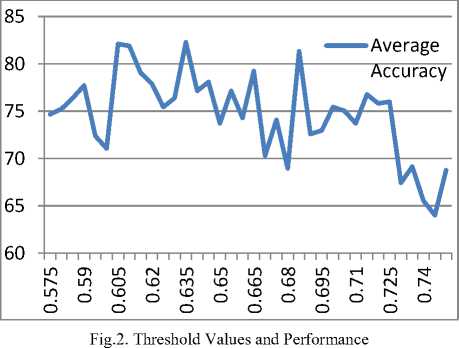
After several iterations of the symptomatic malaria model with (8 X 10 X 2) NN Simulation Structure of the classification algorithm a step size of 0.005 was stabilized to get the local and global maxima concentrated within the region 0.575 to 0.750 output ranges. Figure 3 depict the optimum training threshold Values and Performance on the Training dataset. Table 4. depicts the definition of terms used in taking records of the model. At overall training, the best threshold value of 84.57 at 0.58 was obtained as shown in Fig.3 and Table 5.

Best Training

100 > ro

<

Accuracy

0.655   0.62   0.605   0.58 Threshold

Fig.3. Best Threshold Values and Performance for the developed FeedForward Back-Propagation (FF_BP) Neural Network Modelon Training Dataset

A step size of 0.005 was taken to get the local and global maxima concentrated within the region 0.575 to 0.750, output ranges. Several threshold values were searched to get the best threshold values. The optimal threshold value is then used to test the FeedForward Neural Network Model using the Malaria Threat and Classification Algorithm.

Table 5. Optimum Threshold Values and Performance for the developed Feed-Forward Back-Propagation Neural Network Model on Training Dataset

Th	AC1	AC2	AC3	AC4	AC5	Avg AC	STD
0.655	77.14286	75.2381	78.09524	78.09524	77.14286	77.14286	1.166424
0.62	82.85714286	81.90476	80	81.90476	78.09524	80.95238	1.904762
0.605	82.85714	82.85714	80	82.85714	81.90476	82.09524	1.241753
0.58	85.71428571	85.71429	85.71429	81.90476	83.80952	84.57143	1.703671

Table 4. Definition of terms

Acronymns	Full Meaning
AC1 --- AC5	Accuracy for 5 runs from 0.575 to 0.7500
Avg AC	Average Accuracy
STD	Standard Deviation
Th	Threshold

Thus the best accuracy for Feed-Forward Back-	threshold frequency 0.58 and 0.715 this was confirmed in
Propagation(FF_BP) Neural Network Model is between	the testing phase in the Table 6(a) below
Table 6 (a). Optimum Threshold Values and Performance for the developed Feed-Forward Back-Propagation(FF_BP)
Neural Network Model on Testing Dataset
Th       AC1       AC2        AC3	AC4         AC5       Avg AC        STD
0.64          80         75.55556       82.22222	77.77778        82.22222       79.55556        2.897423
0.685         80         84.44444       82.22222	86.66667           80          82.66667        2.897423
0.715         80         84.44444       86.66667	86.66667        86.66667       84.88889        2.897423
Table 5(a) the least MSE value obtained was 0.1333	Standard Deviation of 2.897423 and MSE 0.1333 should
and there is consistency of 2.897423 the least standard	not be exceeded. This was confirmed in the overall Best
deviation in the iterations. This consistency indicates that	threshold value and performance depicted in Table 6(b)
to obtain the best accuracy of the model a benchmark of
Table 6 (b). Best Threshold Values and Performance for the developed Feed-Forward Back-Propagation
(FF_BP) Neural Network Model on Testing Dataset
Th         AC1        AC2        AC3	AC4        AC5       Avg AC       STD
0.71         86.66667       86.66667       88.88889	84.44444       91.11111       87.55556       2.533723

T he ANN Training Performance was evaluated with the use of Mean Square Error (MSE). The MSE value obtained was 0.1000 and the best validation performance is 0.10563 which converges at 2^nd Iteration of 8 iterations.

The graph of average accuracy was plotted against threshold values as shown in Fig.4. About twelve (12) local maximum values were obtained and ten (10) local minimum values within 0.575 and 0.7500 threshold ranges. A global maximum is at 0.710 and the highest local minimum is at 0.600.

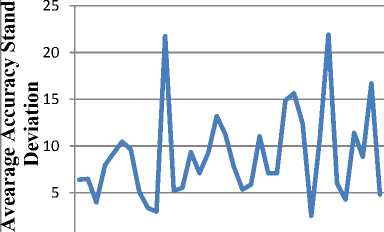
Fig.5. depicts the graph of average standard deviation against threshold values. The least standard deviation of 2.53 was obtained at threshold value 0.710. The highest average accuracy of the model, 87.56% was obtained at threshold value 0.710 with the standard deviation 2.53. The least deviation with the best accuracy was achieved at threshold 0.710 shows the highest reliability and consistency of the threshold.

^ Standard Deviation Vs Threshold Values

Threshold Values

Fig.5. Graph of Average Accuracy Standard Deviation against Threshold Values

у^

и 90

и 80

ы70

Accuracy Vs

Threshold

шсптгмтттсотнт^ ^lЛOЦ)mUDЦ)UDCn^<^l^

.0.0. о о о . о о о о о о о

Threshold Values

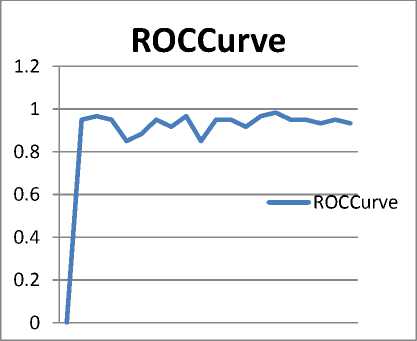
Fig.6. The ROC Representing Malaria Feed Forward Neural Network Detector Performance

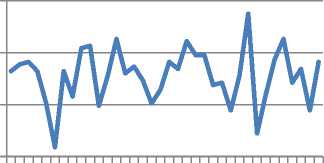
Fig.4. Graph of Average Accuracy against against Threshold Values

Receiver Operating Curve (ROC ) curves represent graphical summaries of a detector's performance. Here is the ROC Curve of Malaria Feed Forward Neural network in Fig.6. The Area Under the Curve(AUC) is 0.8667. The maximum AUC is 1, which corresponds to perfect classifier. Larger AUC values indicate better classifier performance.

• VIII.    Result Discussion

Multilevel thresholding was conducted to get the optimum thresholds with the best accuracy at lowest standard deviation and mean square error. The best accuracy of 87.56% was achieved at the threshold level 0.710 with ability of test to identify the infected cases of 96.67 and ability to separate the infected cases from non infected cases is 76.67%. From the Feed-Forward Back-Propagation(FF_BP) Neural Network Malaria Model, 0.710 threshold values indicates that only 71% of the female Anopheles mosquitoes that go for a blood meal survive to lay their eggs at the end of that cycle as they subjected to monthly average daily temperature, rainfall and relative humidity. Temperature is a key factor, once the temperature falls to the sporogonic cycle threshold (18°C) the mosquito’s lifespan may be reduced for the sporogonic cycle to be completed. Most agricultural models use 10-20 mm of rainfall as the threshold meaning no malaria would occur below this level, so 10 mm is used as the threshold amount in these model runs. The effect of rainfall and Temperature is the resulting factor of relative humidity on the model. From the developed ANN model to detect symptomatic and climatic based malaria disease, specificity 76.67% achieved shows that the ability to separate the non infected cases (Class 0) of malaria disease is higher than infected cases. Thus, this research should be improved on by developing an enhanced model that can accurately separate the classes of infected cases. So a hybrid method that complements the weaknesses of one algorithm with the strengths of other and combines the cooperative and competitive characteristics of the individual techniques to produce more accurate results than the individual techniques is proposed.

• IX.    Conclusion

This study has developed a machine learning approach to classify malaria cases according to its severity using Artificial Neural Network in MATLAB Environment. Vector threat and transmission threat are the major threat of symptomatic malaria infections. Factors that contributes to having malaria such as climatic factors; temperature, rainfall and relative humidity were all explored. These factors combined with the symptomatic clinical features were all considered as input features to the machine learning models. This Malaria Feed-Forward Back-Propagation (FF_BP) Neural Network Model proposed can handle dynamics of symptomatic characteristics of malaria parasite with effects of climatic factor which is a great determinant of malaria severity. The model will stand as an alternative cheap and fast healthcare solution and will benefit patient, medical personnel and any individual to perform malaria diagnosis severity in unreachable or underdeveloped areas. Taking effective decision like appropriate medication to prescribe will be guarded by the model. Also this research will benefit the patient by reducing the waiting response time being spent in the hospital.

Acknowledgement

This research was sponsored by Local TETFUND Grant offered by Federal University of Technology, Minna, Niger State, Nigeria.