Сжатие гиперспектральных данных на основе метода кодирования с преобразованием

В ряду задач обработки данных особое место занимают задачи, связанные с дистанционным зондированием Земли из космоса. В последнее время наибольший интерес вызывают так называемые гиперспектральные данные (или изображения), представляющие собой трёхмерный массив, состоящий из множества изображений одного и того же участка земной поверхности, полученных в разных спектральных диапазонах (см. рис. 1).

Рис. 1. Пример гиперспектральных данных

Очевидно, что объём каждого гиперспектрального изображения весьма велик, что приводит к сложностям при хранении и передаче таких данных. В этой связи особенно актуальной становится задача их сжатия.

Среди известных методов сжатия изображений наиболее широко распространён метод кодирования с преобразованием, который реализован, в частности, в стандарте (алгоритме) JPEG. Однако JPEG, хотя иногда и используется для сжатия гиперспектральных данных, оказывается в этом случае недостаточно эффективным.

В настоящей работе предлагается новый метод (и вытекающий из него алгоритм) сжатия, являющийся обобщением известного метода кодирования с преобразованием на случай трёхмерных гиперспектральных данных.

Обобщённый метод кодирования с преобразованием

Метод кодирования с преобразованием (см., например, п. 6.5 монографии [1]), применяемый для двумер- ных изображений, состоит из следующих этапов. Изображение разбивается на квадратные блоки размером N×N пикселей. В каждом блоке выполняется дискретное преобразование, в результате которого формируется набор спектральных коэффициентов – трансформант. Из полученных трансформант отбираются наиболее существенные (обычно по дисперсионному критерию), вы- полняется их квантование и кодирование.

Дискретное преобразование должно удовлетворять требованиям обратимости и концентрации информации в малом количестве трансформант. Как правило, на практике используется дискретное косинусное преобразование (ДКП), которое полностью отвечает сформулированным требованиям и, кроме того, имеет быстрый алгоритм вычисления.

На этапе восстановления (декодирования) произ- водится процедура декодирования и деквантования обобщённых координат. После этого для каждого блока вычисляется обратное преобразование и восстанавливаются пиксели изображения.

Нами предлагается обобщение описанного выше метода на случай трёхмерных гиперспектральных данных. Будем понимать под гиперспектральным изображением трёхмерный массив значений яркости:

{ f ( „ 1 , П 2 , П 3

N ! - 1, N 2 - 1, N 3 - 1

„ 1 , „ 2 , П з = 0

где N1, N2 – пространственные размеры изображения (высота и ширина соответственно), N3 – количество спектральных каналов.

На первом шаге массив данных разбивается на не-пересекающиеся блоки. В каждом блоке выполняется ДКП, которое в трёхмерном случае будет иметь вид:

F ( m 1 , m 2 , m₃ ) =

N - 1 N - 1 N - 1

= E EE f ( n1, n 2, n 3 ) hm, ( n1 ) hm 2 ( n 2 ) hm 3 ( n3 ), n1 =0 „2 =0 пз =0

где hm (n) = ^m cos

n ( 2 n + 1 ) m

2 N

X m

1^П при m = 0, 2^ П при m ^ 0.

Следующим этапом является отбор и квантование существенных трансформант. Каждая трансформанта квантуется и кодируется двоичными словами длины bm1,m2,m3, где (mi,m2, m3) — номер трансформанты в блоке. Суммарная длина всех кодовых слов b = Z bm m определяется требуемым коэффициентом сжатия.

Отбор существенных трансформант может сводиться к распределению общего количества бит b по отдельным трансформантам. Будем предполагать, что каждая трансформанта F ( m 1 , m ₂, m 3 ) при некотором фиксированном ( m 1 , m ₂, m 3 ) , отличном от (0,0,0), имеет нормальное распределение. В этом случае при сжатии изображений для распределения бит используют квазиоптимальный алгоритм, основанный на так называемом «законе логарифма дисперсий» [2], [3]. В настоящей работе он обобщён на случай трёхмерных данных. Также адаптирован для работы с трёхмерными данными квантователь Ллойда–Макса [2], обеспечивающий минимум среднеквадратичной ошибки восстановления. Из квантованных значений каждого блока окончательно формируются сжатые данные.

Отметим, что предложенный подход к сжатию и блочному хранению сжатых данных позволяет восстанавливать как все данные целиком, так и отдельные пространственные срезы или кривые спектрального отражения в заданной точке.

Экспериментальное исследование

В рамках работы было проведено экспериментальное исследование предложенного метода сжатия.

Исследование проводилось на общедоступном наборе гиперспектральных изображений [4], сделанных сканером «Aviris» в 2006 году (этот сканер обеспечивает съёмку в 224 спектральных каналах с длиной волны от 400 до 2500 нм). Для экспериментов были взяты изображения с пространственным разрешением 680×512 пикселей. Каждый пиксель кодируется 16 битами. На рис. 2 приведено одно изображение из этого набора в спектральном канале №64.

Рис. 2. Изображение типа «ландшафт» (сцена №0) в спектральном канале №64

Основной целью данной работы является проверка эффективности трёхмерного подхода в рамках выбранного метода сжатия. Поэтому в качестве базы для сравнения был выбран алгоритм послойного сжатия. Его основой является представление гиперспектрального изображения как набора двумерных изображений и использование сжатия для каждого слоя-изображения по отдельности. Для сжатия двумерного слоя использовалось блочное двумерное ДКП размером 8×8, выполнялся отбор и квантование существенных трансформант. Коэффициент сжатия определялся для всего гиперспектра в целом.

На рис. 3 приведено сравнение разработанного алгоритма с методом послойного сжатия. Построены зависимости пикового отношения сигнала к шуму от задаваемого коэффициента сжатия. В контексте данной работы под «шумом» понимается погрешность, вносимая процедурой сжатия и восстановления изображения. По полученным результатам можно сделать вывод, что с ростом коэффициента сжатия трёхмерный алгоритм обеспечивает существенно более высокое качество восстановленных данных, чем двумерный подход.

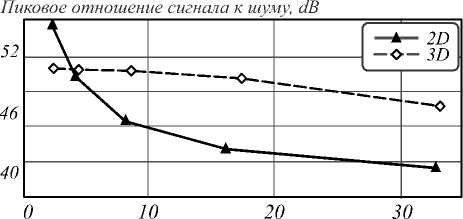
Коэффициент сжатия

Рис. 3. Сравнение двумерного и трёхмерного алгоритмов для изображения типа «ландшафт»

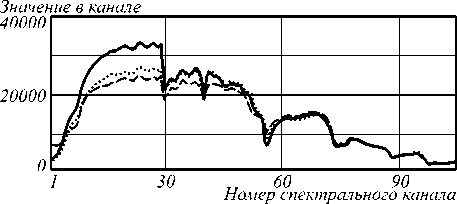
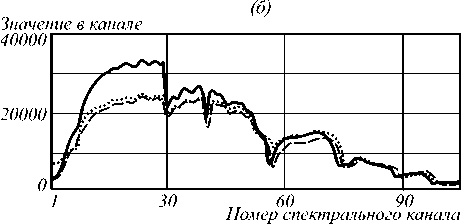
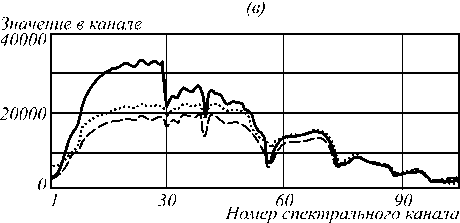
Для оценки визуального качества на рис. 4 показаны восстановленные изображения для трёхмерного подхода (а), (б), (в) и двумерного послойного сжатия (г), (д), (е) при коэффициентах сжатия 4, 16 и 64 соответственно.

При малых коэффициентах сжатия двумерный подход даёт хорошие результаты, однако с ростом этого параметра качество восстановления существенно снижается, а при высоких значениях становится вообще неприемлемым. При этом трёхмерный подход демонстрирует хорошее качество восстановления.

Одной из важнейших задач в рамках анализа гиперспектральных изображений является получение кривой спектрального отражения для какой-либо пространственной точки. На рис. 5 приведены результаты восстановления кривой спектрального отражения сцены №18 для пространственных точек с координатами (280, 340) и (650, 120). Показаны кривые для значений коэффициента сжатия, равных (а), (г) – 4, (б), (д) – 16, (в), (е) – 64. Выбран такой диапазон каналов, в котором отличие исходной и восстановленных кривых проявляется наиболее заметно.

По полученным результатам можно сделать вывод, что при восстановлении спектральной кривой могут появляться существенные искажения на тех участках кривой, где значения сильно отличаются от математического ожидания соответствующих трансформант. Это общая проблема всех методов сжатия, работающих по критерию среднеквадратичной ошибки. Однако форма кривой и расположение минимумов-максимумов при этом сохраняются. При малых коэффициентах сжатия двумерный подход оказывается несколько лучше трёхмерного, однако с ростом коэффициента сжатия трёхмерный подход показывает более высокое качество восстановления.

В целом полученные результаты показывают существенное улучшение восстановления данных за счёт использования трёхмерного подхода.

Сравнение с другими подходами

Несмотря на то, что тематика обработки гиперспектральных данных сейчас весьма популярна, публикаций на тему их сжатия весьма немного. В работе [5] рассматривается метод иерархической сеточной интерполяции, ориентированный на контроль максимальной ошибки в каждом пикселе. Однако этот метод эффективен для сравнительно небольших коэффициентов сжатия при несущественных искажениях, вносимых в гиперспектральные данные.

Трёхмерный подход

а)

б)

в)

Рис.4. Восстановленное изображение типа «ландшафт» (сцена №18) в спектральном канале №64 для коэффициентов сжатия 4, 16, 64

Двумерный подход

Точка с координатами (280, 340) (а)

------ Исходная спектральная кривая

............. Спектральная кривая после ЗВ-сжатия

----Спектральная кривая после 2В-сжатия

Точка с координатами (650, 120)

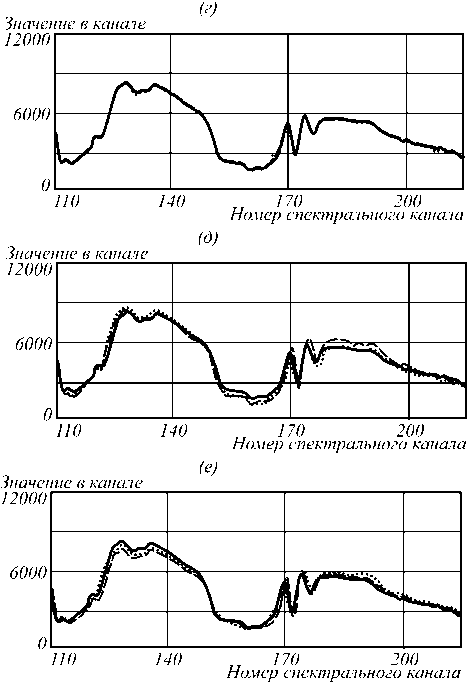
Исходная спектральная кривая

Спектральная кривая после ЗВ-сжатия

Спектральная кривая после 2В-сжатия

Рис. 5. Восстановление спектральной кривой отражения точек сцены №18 для коэффициентов сжатия 4, 16, 64

В работах [6], [7], как и в данной работе, в качестве критерия качества принято пиковое отношение сигнала к шуму. В первой работе использовалось двумерное кодирование с преобразованием по пространственным координатам и дифференциальная импульсно-кодовая модуляция по спектральной координате (будем обозначать этот алгоритм как 2D-DCT). Во второй работе исследовалось сжатие гиперспектральных изображений с помощью трёхмерных вейвлет-преобразований (будем обозначать этот алгоритм как 3D-Wavelet). На рис. 6 приведено сравнение разработанного алгоритма с этими подходами.

При высоких коэффициентах сжатия рассмотренный в работе метод кодирования с трёхмерным преобразованием обеспечивает значительно более высокое качество восстановления, чем кодирование с трёхмерным вейвлет-преобразованием, и немного хуже, чем метод 2D-DCT.

Заключение

Таким образом, в работе предложен новый метод сжатия гиперспектральных изображений и алгоритм, вытекающий из данного метода, которые обобщают двумерный метод кодирования с преобразованием на

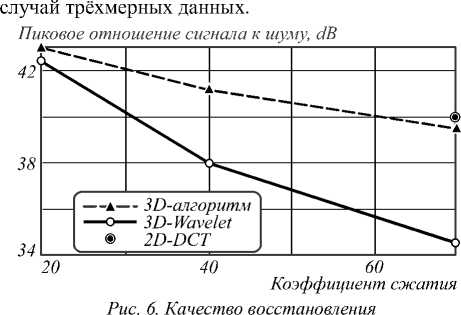
различных алгоритмов сжатия

Предложенный подход к сжатию и блочному хранению сжатых данных позволяет восстанавливать из архива как все данные целиком, так и отдельные пространственные срезы или кривые спектрального отражения в заданной точке. Выбраны параметры предложенного метода и произведено его исследование.

В рамках исследования проведено сравнение с двумерным послойным сжатием гиперспектральных данных. Продемонстрировано преимущество трёхмерного подхода. В частности, показатель пикового отношения сигнала к шуму при одних и тех же коэффициентах сжатия снижается приблизительно на 30% за счёт использования трёхмерного подхода. Визуальное качество восстановленных пространственных срезов становится существенно выше. Появляется возможность работы с высокими коэффициентами сжатия (больше 64) при приемлемом качестве восстановления.

Сравнение с известными методами, ориентированными именно на сжатие гиперспектральных данных, также показывает некоторое преимущество разработанного метода.

Работа выполнена за счёт Российского научного фонда (РНФ), грант №14-31-00014 «Создание лаборатории прорывных технологий дистанционного зондирования Земли».