Сжатие изображений с использованием многослойного персептрона
Автор: Лзин Илья Александрович, Соловьв Алексей Вячеславович
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 4-4 т.18, 2016 года.
Бесплатный доступ
В статье описан подход к сжатию цветных изображений с использованием многослойного персептрона. Описывается алгоритм сжатия цветных изображений. Анализ различных структур нейронных сетей показывает зависимость показателей сжатия от количества слоев и числа нейронов в них. В статье приводятся результаты исследования качества сжатия и определяется оптимальная структура нейронной сети для решения задачи сжатия.
Сжатие изображений, нейронная сеть, многослойный персептрон, архитектура "бутылочного горлышка"
Короткий адрес: https://sciup.org/148204767
IDR: 148204767 | УДК: 004.896
Текст научной статьи Сжатие изображений с использованием многослойного персептрона
Сжатие изображений является одной из актуальных задач, решаемых информационно-вычислительными системами. Сжатие способствует экономии ресурсов памяти, требуемых для хранения изображений, или сокращению трафика при их передаче.
Существует немало детерминированных алгоритмов, в той или иной степени отвечающих различным требованиям области, в которой они применяются. Например, JPEG хорошо подходит для сжатия фотографий, реалистичных картин; RLE эффективен при сжатии схематичных рисунков, содержащих блоки пикселей одного и того же цвета; для сжатия изображений “в векторе” обычно используется алгоритм Хаффмана. Все эти алгоритмы не универсальны, так как разработаны для сжатия изображений определенного рода.
Таким образом, поиск новых технологий и средств сжатия изображений по сей день является актуальной задачей. В данной работе используется искусственная нейронная сеть многослойный персептрон [1]. Целью работы является сравнение качества решения задачи сжатия для систем, использующих одну или три сети выбранной модели. Сами сети будут отличаться структурой (количеством и составом скрытых слоев) и коэффициентом, определяющим скорость обучения.
Для решения поставленной задачи создана автоматизированная система, предоставляющая пользователю возможность задать количество используемых для сжатия сетей, определить их структуру, обучающую выборку и коэффициент, определяющий скорость обучения. В системе реализован алгоритм обратного распространения ошибки [2]. На любом этапе обучения сеть можно использовать для сжатия и восстановления
изображения. При этом пользователь увидит на экране численные оценки потерь качества изображения, а также три изображения: исходное, результирующее и их графическую разницу.
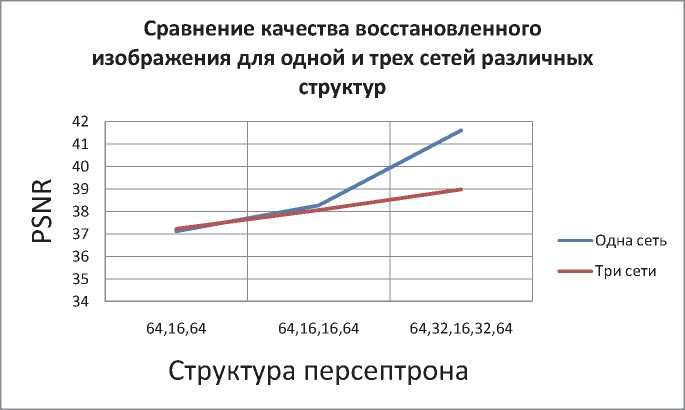
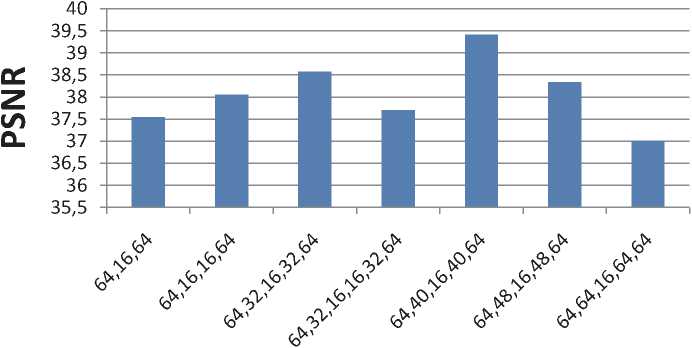
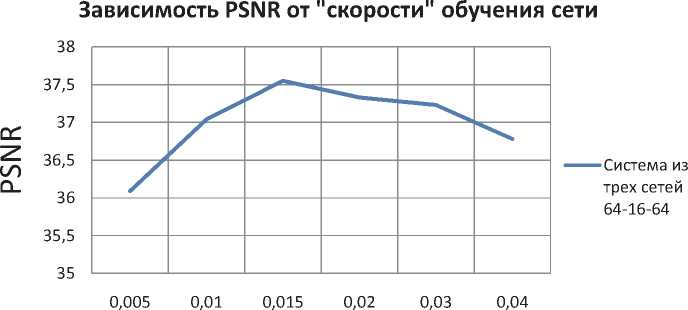
Многослойный персептрон с архитектурой «бутылочного горлышка» – нейросетевая модель, часто используемая для сжатия различных данных, в том числе и изображений. Такой тип архитектуры определяется одинаковым и наибольшим числом нейронов (n) на входном и выходном слоях и одним или несколькими скрытыми слоями, число нейронов на которых постепенно уменьшается к центральному слою, на котором число нейронов (m) наименьшее. Причем m< к = —. (1) т Суть применения такой сети заключается в следующем: на входной слой сети подается вектор входных сигналов (кадр) x=(x1,x2,x3,…,xn), с распространением сигналов по сети от слоя к слою происходит сначала сжатие (до самого малочисленного скрытого слоя, вектор выходных сигналов которого представляет собой сжатый фрагмент) u=(u1,u2,u3,…,um), а затем восстановление исходного кадра y=(y1,y2,y3,…,yn), (до выходного слоя, количество нейронов на котором такое же, как и на входном). Решение задачи сжатия цветного изображения аналогично решению задачи сжатия изображения в оттенках серого. Отличие заключается в том, что для сжатия каждого кадра цветного изображения одной или тремя сетями обрабатываются три вектора входных сигналов вместо одного (как для изображения в оттенках серого), каждый из которых характеризует интенсивность цветовых составляющих пиксела: красной, зеленой и синей компонент. В данной работе все изображения разбивались на кадры 8х8 пикселей и сжимались с помощью сетей, количество Рис. 1. Схема алгоритма сжатия и восстановления изображения нейронов на входных и выходных слоях которых было равно 64. На рис. 1 изображена схема алгоритма покадрового получения сжатого и восстановленного изображения нейронной сетью с возможностью обучения. В приведенной схеме используются следующие обозначения: frames – массив векторов входных сигналов, полученный из кадров сжимаемого изображения; layers – массив массивов выходов нейронов каждого слоя сети; links – массив матриц синаптических весов нейронов каждого (кроме входного) слоя сети; ConstructImg(array, q) – функция, покадрово конструирующая результирующее изображение по массиву выходных сигналов сети array и номеру кадра q. В роли численных оценок потерь качества изображения используется среднеквадратичное отклонение (СКО) и пиковое отношение сигнала к шуму (PSNR) [3]. PNSR определяется следующим образом: PSNR = 20log10^-, (2) где MAXI – это максимальное значение, принимаемое пикселем изображения (когда пиксели имеют разрядность 8 бит, MAXI равно 255), a δ – это среднеквадратическое отклонение, которое вычисляется по формуле: $ = j^^A^dd2 , (3) где yi – значение интенсивности i-го пикселя восстановленного изображения, di – значение интенсивности i-го пикселя исходного изображения, n – размер изображения. Для цветных изображений с тремя компонентами RGB на пиксель СКО считается по всем трем компонентам (и делится на утроенный размер изображения). В ходе работы исследовалась зависимость качества восстановленного изображения от количества используемых сетей (одна универсальная или по одной сети для работы с каждой из трех цветовых компонент), от коэффициента, определяющего скорость обучения сети, от количества и состава скрытых слоев, от характеристик исходного изображения. Для первого исследования были созданы и обучены 12 персептронов: по 4 для каждой из трех выбранных структур сети (64-16-64, 64-16-16-64, 64-32-16-32-64). Одна из этих четырех сетей использовалась в качестве универсальной, другие три работали совместно: каждая – над одной из трех цветовых компонент изображения. На рис. 2 представлен график зависимости PSNR от структуры персептронов для одной и трех сетей, из которого видно, что система из трех сетей справляется с задачей сжатия несколько лучше. Это можно объяснить различными закономерностями в распределении каждой из трех цветовых компонент изображения. Рис. 2. График зависимости PSNR от структуры персептронов для одной и трех сетей Так как система из трех сетей показала лучшие результаты, все дальнейшие исследования будут проводиться на ее примере. Следующее исследование, направленное на нахождение наилучшего коэффициента (a), определяющего скорость обучения сети, проводилось на примере системы, сети которой имели один скрытый слой из 16 нейронов (коэффициент сжатия K=4.0). В табл. 1 представлены средние значения СКО и PSNR, соответствующие системам, сети которых обучались с различной «скоростью». Ниже, на рис. 3, представлен соответствующий график для PSNR. По полученным данным сделан вывод, что наилучший результат показывают сети, при обучении которых использовался коэффициент a, равный 0,015. Теперь все дальнейшие исследования будут вестись с использованием этого значения. На рис. 4 представлена гистограмма, составленная по данным, полученным в ходе иссле- Таблица 1. Анализ качества восстановления сжатых изображений сетями, обученными по алгоритму обратного распространения ошибки с различными значениями коэффициента a Коэффициент a СКО PSNR 0,005 4,0 36,09 0,01 3,59 37,04 0,015 3,38 37,55 0,02 3,47 37,33 0,03 3,51 37,23 0,04 3,69 36,78 Коэффициент, определяющий скорость обучения сети Рис. 3. Зависимость PSNR от коэффициента a Структура персептрона Рис. 4. Зависимость PSNR от структуры используемых сетей дования зависимости качества решения задачи сжатия от структуры используемых сетей. Из гистограммы видно, что наилучшие результаты показала сеть, число нейронов на слоях которой равномерно уменьшается к «центру», а затем так же равомерно увеличивается от «центра» к выходу сети (64-40-16-40-64). Исследования показали, что нейросетевая система лучше справляется с задачей сжатия при работе с изображениями с низкой резкостью и контрастностью. Изображения с резкими контурами и высокой контрастностью (например, изображение текста) при сжатии терпели гораздо большие потери, нежели изображения без резких контуров и цветовых переходов.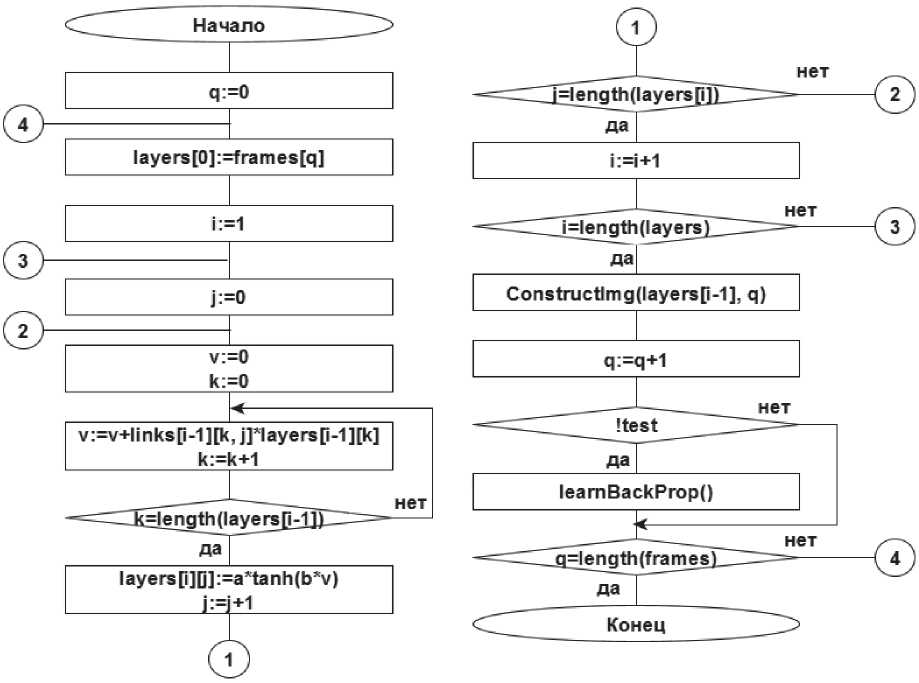
Список литературы Сжатие изображений с использованием многослойного персептрона
- Осовский С. Нейронные сети для обработки информации. М.: Финансы и статистика, 2002. 344 с.
- Хайкин С. Нейронные сети: Полный курс. . 2-е изд. М.: Вильямс, 2006. 1104 с.
- Пиковое отношение сигнала к шуму . URL: https://en.wikipedia.org/wiki/Пиковое_отношение_сигнала_к_шуму (дата обращения 25.02.2016).
- Солдатова О.П., Шепелев Ю.М. Сжатие визуальных данных с использованием многослойного персептрона//Перспективные информационные технологии (ПИТ 2015), Том 1: труды Международной научно-технической конференции . Самара: Издательство Самарского научного центра РАН, 2015. 360 с.


