Сжатие света в двухатомной модели Джейнса - Каммингса с зависящим от интенсивности атом-полевым взаимодействием

Исследование сжатых состояний света – одно из наиболее перспективных направлений в современной квантовой оптике [1; 2]. Такие состояния привлекают особое внимание не только потому, что они позволяют глубже понять природу электромагнитного поля, но и благодаря их широким возможным применениям для высокоточных оптических измерений, оптической связи, квантовых вычислений и др. [2]. Особенно перспективными представляются возможности применения сжатого света в детекторах гравитационных волн. Такое предложение было сделано еще 25 лет назад, но только в последнее время появилась возможность реализации такого проекта с использованием сжатого света [3]. Сжатые состояния света являются также потенциальной основой для множества информационно-квантовых протоколов с непрерывными параметрами [4].

Экспериментально сжатие света было впервые реализовано в 1985 году в нелинейном процессе четырехволнового смешения света в оптическом резонаторе [5]. Позднее для генерации сжатых состояний электромагнитного поля использовались различные нелинейные оптические процессы: оптические параметрические процессы, эффект Керра и др. [1]. В настоящее время выполнено большое число экспериментов по наблюдению сжатых состояний света в различных нелинейных оптических средах. Наиболее перспективными методами получения сжатого света считаются вырожденное параметриче- ское усиление и вырожденное четырехволновое смешение света [2]. Однако для получения значительной степени сжатия света нужны сильно нелинейные среды и малые затухания и избыточные шумы. К сожалению, в современном эксперименте не удается выполнить оба этих условия одновременно, поэтому поиск альтернативных схем получения сжатого света имеет большое практическое значение.

В настоящее сжатие света реализовано также для системы атомов в резонаторе. При наличии точного резонанса моды резонаторного поля с атомным переходом система атомов представляет собой сильно нелинейную среду, в которой возможна генерация сжатого света. Имеются две группы экспериментов по наблюдению сжатых состояний света для пучков атомов в резонаторе. В эксперименте [6] использовались пучки атомов Na, а в работе [7] – атомные пучки Ba. При этом максимальное уменьшения уровня шума для резонаторного поля в указанных экспериментах составило примерно 20 %. Для теоретического описания сжатого состояния моды поля, взаимодействующей с атомами в резонаторе, необходим полный анализ квантовой динамики атомной и полевой подсистем. Хорошо известно, что простейшей нетривиальной моделью, позволяющей описать квантовые эффекты излучения атома в резонаторе, является модель Джейнса – Каммингса, описывающая двухуровневый атом, взаимодействующий с выделенной модой квантованного электромагнитного поля. В рам ках этой модели и ее простейших обобщений могут быть описаны практически все основные квантовые эффекты, возникающие при взаимодействии излучения с веществом, в том числе и сжатие света [8]. В настоящее время интерес к таким моделям перестал быть чисто теоретическим, поскольку реализация одноатомного однофотонного и двухфотонного мазера и микролазера [9; 10] предоставила возможность непосредственного исследования таких систем и экспериментальной проверки основных положений квантовой электродинамики. Модель Джейнса – Каммингса была реализована также на ионах в магнитных ловушках, на квантовых точках, примесных спинах и в сверхпроводящих системах [11].

Возможность сжатия света в модели Джейнса – Каммингса была впервые предсказана в работе [12]. Для описания генерации сжатого света пучками атомов в резонаторах естественно рассмотреть многоатомную модель Джейнса – Каммингса. При этом аналитические выражения для параметра сжатия могут быть получены только для моделей, состоящих из нескольких атомов, взаимодействующих с полем в резонаторе. Сжатие света в простейшей системе двух двухуровневых атомов с различными типами переходов в идеальном резонаторе в случае вакуумного, когерентного и теплового состояний резонаторного поля было рассмотрено в [13–15]. В работе [16] показано, что поглощение и испускание атомами фотонов в резонаторе в случае достаточно интенсивных резонаторных полей приводит к заметному изменению параметра атом-полевого взаимодействия. Следовательно, для адекватного анализа динамики атомной и полевой подсистем в резонаторе необходим учет зависимости параметра взаимодействия атомов и поля от интенсивности резонаторного поля. В настоящей работе исследованы особенности сжатия света для двухатомной модели Джейнса – Каммингса с зависящим от интенсивности поля параметром атом-полевого взаимодействия для различных начальных интенсивностей резонаторного поля и различных начальных состояний атомной подсистемы.

Рассмотрим систему двух двухуровневых атомов с частотой атомного перехода too, взаимодействующих с модой квантового когерентного электромагнитного поля с частотой to. Предположим наличие в системе точного резонанса too = to. Тогда гамильтониан взаимодействия изучаемой системы в дипольном приближении и приближении вращающейся волны можно за- писать в виде

+                                  +

H int = ^й g ^ 1 V a aa с ^- + с + a

где a+(a) — оператор рождения (уничтожения) фотона резонаторной моды; с+(сi) — повышаю- щий (понижающий) оператор в i-м двухуровневом атоме и величина gVa+a представляет собой параметр атом-фотонного взаимодействия, за- висящий от интенсивности резонаторного поля. Обозначим через | +) и | -) возбужденное и основное состояния одиночного атома, а через | n) — фоковское состояние моды резонаторного поля. Тогда двухатомная волновая функция есть комбинация состояний | Vi, V2) = | Vi) | V2), где v = +, -. Пусть атомы приготовлены в начальный момент в произвольной чистой суперпозиции базисных векторов

| ^(0)) = a | +, +) + P | +,-) + У I -,+) + 8 | -,-), где a, P, y, 8 — произвольные комплексные числа, удовлетворяющие условию нормировки

I a I2 + I в I2 + I Y I2 + I 8 |2 = 1, а резонаторное поле – в одномодовом когерентном состоянии to

I o) = E C n I n ) .

n = 0

Здесь n/2

Cn = exp( - n / 2) n= e^{l ф} ,

V n !

где n — среднее число фотонов в моде, а ф — фаза когерентного состояния.

Точное решение временного уравнения Шредингера для модели с гамильтонианом (1) для выбранных начальных условий имеет вид

| Т(t)) = £[ An (t) | +, +) + Bn (t) | +, -) + n                                           (2)

⁺ C n ⁽ t ) | ^- , ^{+) +} D n ⁽ t ) | ^- , ^-)] | ^{n )} .

Здесь использованы следующие обозначения

A n ( t )=

(n + 2)2 + (n + 1)2 cos(2Qnt) 2nn aF -a± n

. ( n + 1)sin(2 Q ) iⁿ

-

i

( n + 1)sin(2 Q _nt ) 2 o n

Y F n + 1

( n + l)C n + 2)sin²( ^ n ^t )

8 F n + 2 ,

B n ( t )=

= - i

n sin(2 Q _n - i t ) 2 ^ n - 1

a F n — 1 + cos²( Q n - i t ) P F n

-

-

sin²( Q n - i t ) y F n - i

⁽ n + l)sm²⁽ Q n — i t ) 2 Q n - i

5 F n + 1 ,

C n ( t )=

= - i

n sin(2 Q _n - i t ) 2 ^ n - i

^{a F} n - i

- sin 2 ^{( Q} n - i t ) P F n +

⁺ Cos 2 ^{( Q} n - i t ^{) y} F n ^- i

⁽ n ⁺ ^sm ²^ n - i t ) 2 Q n - i

5 F n + i ,

Sl(£)

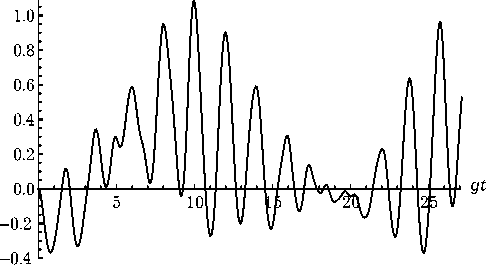
Рис. 1. Длинновременное поведение параметра сжатия S i для модели с n = 0,5. Атомы в начальный момент времени находятся в состоянии | - , -)

D n ₍ t ) = - O n -O n in²^ „ F n - 2 Q n - 2

-

n sin(2 Q _n - 2 1 ) 2 Q n - 2

в F n - i -

-

n sin(2 Q _n - 2 1 ) 20^ 2

Y F n - i ⁺

+

^{(( n} - ^{i)2 + n 2)}cos ²№ n - 2 t ) 2 Q n - 2

5 F n ,

где

Q _n = [ 2 n ( n + 3) + 5 ] /2.

Для того чтобы исследовать возможность сжатия моды поля, введем стандартным обра-

зом медленно меняющиеся квадратурные компоненты для моды резонаторного поля

X_i = (i/2)( ae i ® t + a ⁺ e ^- i ^ю t ),

X ₂ = (i/ 2 i)(ae i ^ю t - a ⁺ e ^- i ^ю t ).

Поскольку квадратурные компоненты удовлетворяют коммутационному соотношению [ X _i, X ₂ ] = i /2, соотношение неопределенностей для них прини-

мает вид

(AXi)2(AX2)2 > i / i6, где (AX,)2 =(X2)-(Xi)2 (i = i,2) — дисперсии квадратурных компонент. Как известно, сжатое состояние минимизирует соотношение неопределенностей для квадратурных компонент. При этом для одной из компонент (сжатой) выполняется соотношение (AXi)2 < i / 4 (i = i,2). Для проведения численных расчетов удобно ввести так называемые параметры сжатия следующим образом:

S = ^{( A} X i ) ) ^{- i} / 4 = 4( a x ) 2 - i ( i = i , 2) .

i / 4

При таком выборе когерентному и вакуумному состоянию поля в любой момент времени будет соответствовать значение параметра сжатия, равное нулю. Условие S i <  0 для какой-либо из квадратурных компонент будет означать нали-

чие в ней сжатия или уменьшения флуктуаций поля ниже квантового предела. Значению S i = - i соответствует полное отсутствие квантовых флуктуаций в соответствующей квадратурной компоненте. Часто в качестве критерия сжатия используют также величину | S i | x i00 %. Тогда 100 %-ному сжатию соответствует нулевая неопределенность одной из компонент. В терминах операторов рождения и уничтожения фотонов параметры сжатия можно представить в виде

S _i = 2 ( а ⁺ а ) + 2 Re ( а ² e ² i ^ю t ) - 4(Re < ae i ^ю t ) )², (3)

S ₂ = 2 < a ⁺ a ) - 2 Re < a ² e ² i ^ш t ) - 4(Im < ae i ® t ) )². (4)

Используя явное выражение для волновой функции (2), нетрудно вычислить временные зависимости параметров сжатия, определяемые формулами (3) и (4). Указанные соотношения не приведены в настоящей статье из-за их слишком громоздкого вида.

Перейдем к обсуждению результатов численного моделирования временного поведения параметров сжатия для рассматриваемой модели. Временные зависимости параметра сжатия в первой квадратурной компоненте для различных значений среднего числа фотонов в резонаторной моде и атомов, приготовленных в начальный момент времени в основном состоянии | - , -) представлены на рис. 1–4. На рис. 1 показано длинновременное поведение параметра сжатия в первой квадратурной компоненте для малых значений начальных интенсивностей резонаторного поля.

Из рисунка видно, что параметр сжатия S ₁ (аналогично и S ₂) осциллирует во времени, принимая как положительные, так и отрицательные значения. При этом максимальная степень сжатия почти в два раза превосходит максимальное значение степени сжатия в случае обычной

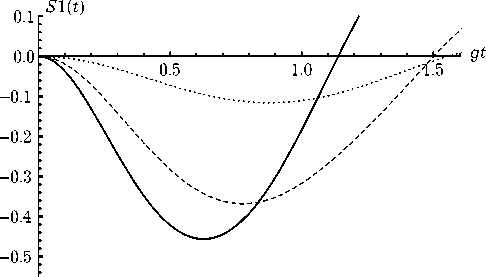
Рис. 2. Коротковременное поведение параметра сжатия S 1 для модели с n = 0,1 (точечная линия), n = 0,5 (штриховая линия) и n = 1 (сплошная линия). Атомы в начальный момент времени находятся в состоянии | — , —)

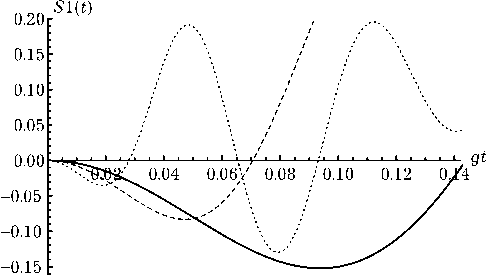
Рис. 4. Коротковременное поведение параметра сжатия S 1 для модели с n = 10 (сплошная линия), n = 20 (штриховая линия) и n = 50 (точечная линия). Атомы в начальный момент времени находятся в состоянии | — , —)

Рис. 3. Длинновременное поведение параметра сжатия S 1 для модели с n = 20. Атомы в начальный момент времени находятся в состоянии | — , —)

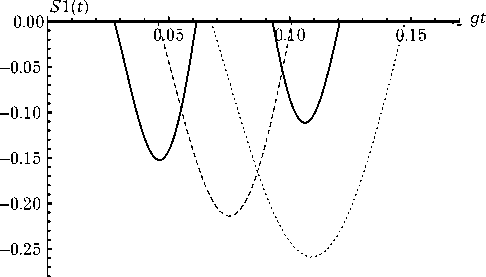
Рис. 5. Коротковременное поведение параметра сжатия S 1 для модели с n = 20 (точечная линия), n = 30 (штриховая линия) и n = 50 (сплошная линия). Атомы в начальный момент времени находятся в состоянии | + , +)

двухатомной модели Тависа – Каммингса для малых начальных средних чисел фотонов в резонаторной моде. На рис. 2 показано коротковременное поведение параметра сжатия S1 в области первого пика для различных малых значений среднего числа фотонов моде. Максимальное значение параметра сжатия в области первого пика достигается для начального среднего числа фотонов n = 1 и составляет примерно 45 %, что более чем в два раза превосходит соответствующую величину в случае обычной модели Джейнса – Каммингса. При дальнейшем увеличении среднего числа фотонов моде n максимальная степень сжатия в области первого пика вначале уменьшается, а затем вновь начинает расти, достигая второго локального максимума для n = 10 (примерно 15 %). При этом для модели с зависящей от интенсивности константой взаимодействия сжатие имеет место и для интенсивных начальных когерентных полей. Заметим, что для стандартной модели сжатие имеет место только для малых значений среднего числа фотонов в моде n < 1 [12; 13]. На рис. 3 показано длинновременное поведение параметра сжатия в первой квадратурной компоненте для n = 20 , а на рис. 4 – коротковременное поведение S1 в области первого пика для модели с n = 10 (сплошная линия), n = 20 (штриховая линия) и n = 50 (точечная линия).

Для стандартной одно- и двухфотонной модели Джейнса – Каммингса сжатие света имеет место только для начального атомов, приготовленных в основном состоянии [12; 13]. Численные расчеты показывают, что для модели с зависящей от интенсивности константой взаимодействия сжатие имеет место для любых начальных состояний атомов. На рис. 5 показано коротковременное поведение параметра сжатия S ₁ в случае возбужденного начального состояния атомов | + , +) для начального среднего числа фотонов n = 20 (точечная линия), n = 30 (штриховая линия) и n = 50 (сплошная линия). Максимальная степень сжатия в первой квадратурной компоненте составляет около 30 % и достигается для модели с n = 15. При этом сжатие в первой квадратурной компоненте возникает с запаздыванием во времени и имеет место для больших интенсивностей резонаторного поля.

Таким образом, в настоящей работе мы детально исследовали особенности сжатия света в системе двух атомов, взаимодействующих с модой квантового электромагнитного поля в идеальном резонаторе, с учетом зависимости параметра диполь-фотонного взаимодействия от интенсивности резонаторной моды. При этом было показано, что такая нелинейная среда является значительно более выгодной для генерации сжатого света в сравнении с системой атомов с однофотонными переходами, поскольку в рассматриваемой среде сжатие возможно для интенсивного начального когерентного поля, которое может быть получено без использования уникального оборудования, и различных начальных состояний атомов. Рассмотрение более реалистичной модели сжатия электромагнитного излучения атомов в неидеальном резонаторе, учитывающей спонтанное излучение и потери фотонов из резонатора на основе подходов, развитых в наших работах [17–19], будет являться предметом нашей следующей работы.