Тарировка многокомпонентного динамометра, выполненного на основе механизма с параллельной кинематикой

При решении ряда технических задач может возникнуть необходимость измерения силовых факторов – сил и моментов относительно заданных осей координат. Такая проблема возникает, например, при анализе взаимодействия режущего инструмента и заготовки в процессе фрезерования. Для определения сил (сил резания) в этом случае используются многокомпонентные динамометры – измерительные приборы, способные регистрировать силы, направленные вдоль некоторых заданных осей, и пересчитывать их в требуемые силовые факторы – силы и моменты сил.

Конструкция типичного представителя многокомпонентного динамометра – прибора 9257B фирмы Kistler (Швейцария) и описание силоизмерительной установки на его основе представлены в [1]. С помощью этого прибора возможно определение трех ортогональных составляющих силы, сонаправленных осям связанной с динамометром системы координат, а также определение моментов сил, действующих вокруг этих осей. Таким образом, измерительная система, построенная с использованием этого динамометра, позволяет определить шесть силовых факторов, полностью оправдывая термин «многокомпонентность».

Основная область использования динамометра 9257B и аналогичных ему приборов – измерение сил, возникающих при обработке материалов методами фрезерования, точения, шлифования и т. п. Однако он может найти применение и в иных областях, связанных с необходимостью измерения силовых факторов, например, при аэродинамических испытаниях моделей летательных аппаратов.

В Южно-Уральском государственном университете ведутся работы по созданию стенда для наземной отработки летательных аппаратов с переменными массо-геометрическими характеристиками. Концепция стенда предполагает размещение летательного аппарата на подвижной платформе, устанавливаемой, например, на легковой автомобиль. При движении автомобиля скорость набегающего потока будет соответствовать наиболее ответственным режимам функционирования летательного аппарата – режимам взлета и посадки.

В рамках наземной отработки летательного аппарата необходимо осуществлять контроль действующих на него силовых факторов. С этой целью предполагается использовать многокомпонентный датчик сил – многокомпонентный динамометр, размещаемый между летательным аппаратом и платформой. При этом динамометр должен обладать необходимым диапазоном и точностью измерений, малой массой (не более 1,5 кг), относительно невысокой стоимостью, возможностью эксплуатации в полевых условиях.

Анализ возможности использования для указанных целей динамометра 9257B выявил следующие негативные моменты:

• –    динамометр имеет массу 7,6 кг, что сопоставимо с массой летательного аппарата (6 кг) и существенно превышает принятые в рамках проекта ограничения;

• –    стоимость динамометра превышает 1 млн рублей;

• –    исполнение динамометра по классу защиты IP67 позволяет использовать его в полевых условиях, однако для его работы требуется многоканальный усилитель 5070А (стоимость – более

700 тыс. рублей), исполнение которого по классу защиты IP40 и необходимость питания от сети 220 В, 50 Гц существенно усложняют организацию измерений в полевых условиях.

Таким образом, возникла потребность создания многокомпонентного динамометра, который бы отвечал перечисленным выше требованиям.

На кафедре автоматизации механосборочного производства имеется положительный опыт создания силоизмерительных систем на основе механизмов с параллельной кинематикой, имеющих шесть степеней свободы – гексаподов [2, 3].

Кинематическая схема механизма-гекса-

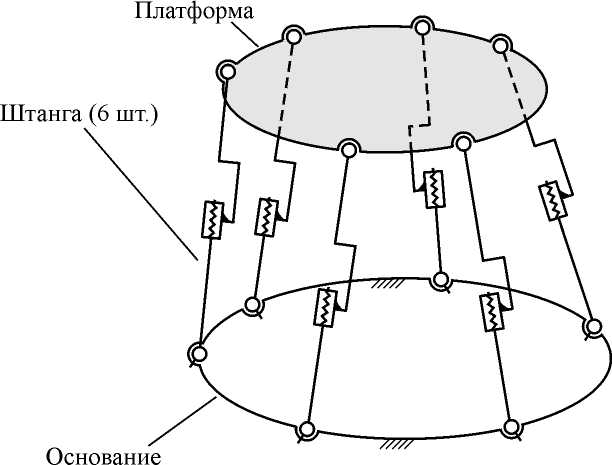
Рис. 1. Кинематическая схема механизма-гексапода

пода показана на рис. 1. Назначение такого механизма – осуществлять перемещение его платформы по шести координатам за счет изменения длин шести штанг. Пространственные механизмы с параллельной кинематикой отличаются высокой удельной жесткостью; в штангах гексапода возникают только усилия растяжения-сжатия, что позволяет упростить конструкцию многокомпонентного динамометра.

Если при использовании гексапода в качестве динамометра не возникает необходимость в изменении пространственного положения его платформы, то целесообразно исключить из конструкции поступательные кинематические пары, т. е. использовать штанги постоянной длины. В качестве штанг выступают силоизмерительные элементы, способные регистри- ровать растягивающие и сжимающие усилия – тензометрические датчики; соединение этих штанг-датчиков с основанием и с платформой осуществляется с использованием однотипных сферических шарниров. Трехмерная модель динамометра показана на рис. 2.

Использование для крепления штанг-датчиков только сферических подшипников позволяет штангам совершать вращения вокруг своих продольных осей, однако на функционировании всей конструкции как многокомпонентного динамометра это не сказывается.

На рис. 3 показана расчетная схема многокомпонентного динамометра; задачей, решаемой при помощи этого прибора, является определение двух векторных величин – вектора силы P и вектора момента M , приложенных к платформе в некоторой точке (точке приведения), по ре-^*

зультатам измерений усилий P_i , осуществляемых с помощью штанг-датчиков.

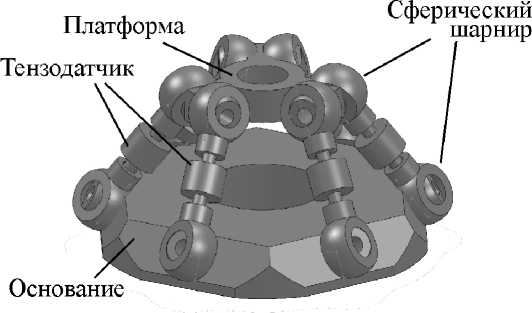
Рис. 2. Трехмерная модель многокомпонентного динамометра

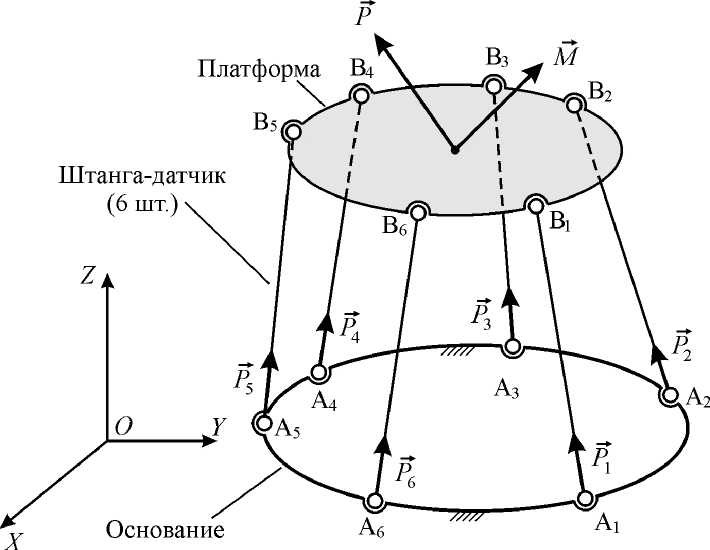
Рис. 3. Схема многокомпонентного динамометра

Уравнения, связывающие подлежащие определению величины P и M с усилиями в штангах, имеют следующий вид:

a ll P l ⁺ a 12 ^P 2 a 21 P l + a 22 ^P 2 a 31 P l + a 32 ^P 2

⁺ a_nP 3 + a i4 P 4 + a i5 P 5 + a^P 6 ^{— -} P x ;

⁺ a 23 ^P 3 ⁺ a 24 ^P 4 ⁺ a 25 ^P 5 ⁺ a 26 ^P 6 ^{— -} P Y ;

+ a 33 P 3 + a 34 P 4 + a 35 P + a 36 P 6 ^{— -} P ,

a 41 P i + a 42 P 2 + a 43 P 3 + a 44 P + a 45 P 5 + a 46 P 6 - M x ,

*

a 51 P l ⁺ a 52 ^P 2 ⁺ a 53 ^P 3 ⁺ a 54 ^P 4 ⁺ a 55 ^P 5 ⁺ a 56 ^P 6 ^{— -} M Y ;

*

a 61 P l ⁺ a 62 ^P 2 ⁺ a 63 ^P 3 ⁺ a 64 ^P 4 ⁺ a 65 ^P 5 ⁺ a 66 ^P 6 ^{— -} M Z ,

——

——

где проекции M ^* включают составляющие, определяемые как моментом M , так и силой P .

Система (1) представляет собой математическую модель динамометра. Правые части в этих уравнениях представляют собой проекции на оси некоторой связанной с основанием динамо-

—

—

метра системы координат OXYZ составляющих внешнего воздействия – силы P и момента M ; коэффициенты a_ij определяются следующими выражениями:

_                xB, - xA,.

'1 J— /              2                22

• 2 ( x A"^x Bj) ^{+ (} y A" y ^B J ) ^{+ ( z} A J ^{- z B} J )

,  __________________zBJ "z A J.

■ 3 J      /                  2                     22 л (Хд —Xr ) +(Уд —Ун ) +(Za —Zr ) A B A B A B

_   ^z J ^x B , ^{- x} A) ^{- x} J ^z B , ^{- z} A)

• У b - У A ,

• ¹2    j ^- 1               2                  2                 2 ;

2 ^{( x} A j ^{- x} B j ) ^{+ ( y} A j ^{- y} B j ) ^{+ ( z} A , ^{- z} B j )

_    У A j ^{( z} B j ^{- z} A j ) ^{- z} A j ⁽ У B j ^- У A j )

• 4    J = /               2                  22^

2^{( x} A ,-^x B , ) ^{+ (} У A , ^- У B , ) + ^z A , ^{- z} B , )

, _    ^x A,( У в , ^- У A,) ^- У A,( ^x в , ^{- x} A,)

Для вычисления коэффициентов a_i необходимо знать координаты ( x A , y A , z A ) и

( x B , y B , z B ) центров сферических шарниров в системе координат OXYZ . Определение этих координат по трехмерной модели многокомпонентного динамометра труда не представляет, однако полученные таким образом значения могут существенно отличаться от координат центров сферических шарниров в реально изготовленном динамометре, что негативно скажется на точности определения величин P и M с использованием модели (1).

Представляется целесообразным определять значения 36 коэффициентов a_i , входящих в систему (1), экспериментально, т. е. решать задачу идентификации параметров модели динамометра.

Рассмотрим первое уравнение системы (1). В него входят шесть коэффициентов a1 , связы вающие усилия в штангах-датчиках с проекцией силы P на ось OX . Для определения этих коэффициентов необходимо провести шесть экспериментов: в каждом из экспериментов формируется известное значение проекции PX и производятся измерения сил P . Таким образом, можно записать следующую систему уравнений:

[ P ₁ < ¹ > a ll p<^2> a_n P1^<3> all P 1 < 4 > a ll P 1 < 5 > a n _ P ! < ⁶ > a_n

• <1>         <1>         <1>         <1>         <1><

• + P2  a12 + P3  a13 + P4  a14 + P5  a15 + P6  a16 —  PX;

• -I- P<2>л   -I- P<2>л   -I- P<2>л -I- P<2>л   -I- P<2>л   — —P<2>■

• + P2 a12 + P3 a13 + P4 a14 + P5 a15 + P6 a16 — PX;

• <3>          <3>          <3>          <3>          <3><

• + P2  a12 + P3  a13 + P4  a14 + P5  a15 + P6  a16 —  PX;

  
  

• < 4>         <4>         <4>         <4>         <4><

• +    P2  a12 + P3  a13 + P4  a14 + P5  a15 + P6  a16 —  PX;

. p<5>_n   . p<5>_л   , p<5>     , p < 5 >      , p < 5 >     __p<5>.

• +    P2  a12 + P3  a13 + P4  a14 + P5  a15 + PP  a16 —  PX;

<6>          <6>          <6>          <6>          <6><

• +    P2  a12 + P3  a13 + P4  a14 + P5  a15 + P6  a16 —  PX,

где верхний индекс обозначает номер эксперимента. Решение системы (2) позволит определить все шесть коэффициентов a 1 .

Если в ходе шести проведенных экспериментов формировались известные значения для всех проекций силовых факторов, присутствующих в правых частях уравнений (1), то с использованием пяти систем уравнений, аналогичных (2), можно определить остальные 30 коэффициентов a_ij .

Проведение экспериментов можно упростить, если осуществлять нагружение платформы такими внешними силами, которые в точке C приводятся только к вектору P < k > . Направление силы P может описываться в системе координат через два угла а и в , рис. 4. На этом рисунке точка

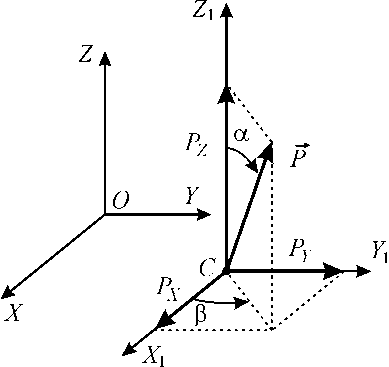
Рис. 4. Задание направления силы P

C – точка платформы, к которой приложена сила P , оси системы координат CX ₁ Y ₁ Z ₁ сонаправлены соответствующим осям системы координат OXYZ .

Тогда проекции силовых факторов можно определить из следующих зависимостей:

P X = P sin а cos в ; P Y = P sin а sin в ; P Z = P cos а ;

**

M X = ^PZ y C - P Y z C ; M Y

*

= PXzC - PZxC ; MZ = PYxC - PXyC , где xC , yC , zC – координаты точки C в системе координат OXYZ .

Для экспериментального определения коэффициентов aij разработано приспособление, модель которого показана на рис. 5. Приспособление имеет неподвижную плоскость, наклоненную к горизонту под известным углом у. Динамометр устанавливается на эту плос- кость. Положение динамометра на плоскости определяется системой двух штифтов, один из которых показан на рис. 5, а.

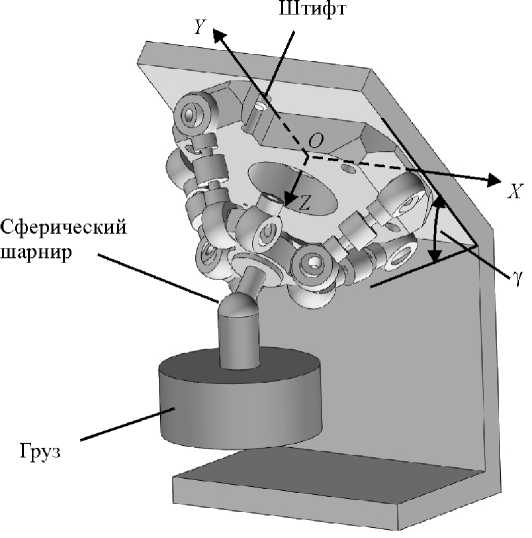
а)

Рис. 5. Приспособление для нагружения динамометра при экспериментальном определении коэффициентов: а – твердотельная модель; б – схема задания системы координат OXYZ

б)

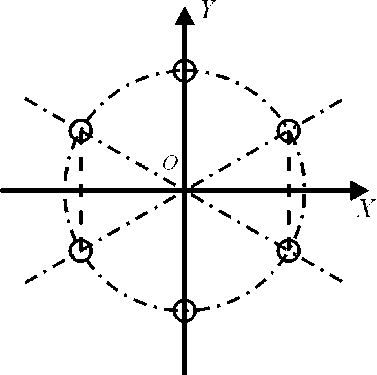
Для базирования по штифтам на основании динамометра выполнены шесть отверстий, лежащих на окружности с шагом 60 градусов (см. рис. 5, б). Отверстия выполнены с высокой точностью, что позволяет использовать их для физического задания связанной с основанием динамометра системы координат OXYZ : ось OY проходит через центры двух отверстий, ось OX проходит через центры двух отрезков, попарно соединяющих центры четырех оставшихся отверстий (см. рис. 5, б), плоскость OXY совпадает с плоскостью контакта приспособления и основания динамометра, ось OZ дополняет тройку осей до правой.

Через сферический шарнир на платформу динамометра будет воздействовать сила веса груза, которая при экспериментах будет являться внешней силой P . Эта сила направлена вертикально вниз; точкой приложения является центр сферического шарнира. Координаты центра шарнира в системе координат OXYZ полагаются известными.

Как отмечено выше, для определения коэффициентов a_ij необходимо провести шесть экспериментов. Примем, что показанное на рис. 5, а положение динамометра относительно приспособления соответствует первому эксперименту. Если ось OX лежит в горизонтальной плоскости (плоскости, для которой вектор силы P является нормалью), то а < 1 > = у и р < 1 > = 90 ° .

Для второго эксперимента необходимо повернуть динамометр относительно приспособления на 60 градусов вокруг оси OZ , для определенности против часовой стрелки. В этом случае а < 2 > = у и р < 2 > = 150 ° . Остальные эксперименты предполагают дальнейшие последовательные повороты динамометра на 60 градусов; для этих экспериментов р < ³ > = 210 ° , р < 4 > = 270 ° , р < ⁵ > = 330 ° , р < ⁶ > = 390 ° . Углы а < k > для всех экспериментов одинаковы и равны у .

В ходе каждого эксперимента должны регистрироваться силы в штангах-датчиках. По результатам экспериментов с использованием зависимостей (2) производится расчет коэффициен- тов aij .

Серия из шести экспериментов является минимально необходимой для определения 36 коэффициентов a_ij , однако из-за неизбежных погрешностей измерений результаты расчетов могут иметь значительные отклонения от действительных значений коэффициентов. Повысить точность решения задачи идентификации модели (1) можно путем увеличения количества экспериментов с последующим использованием известных методов обработки результатов.

Заключение. Разработанный многокомпонентный динамометр позволяет решать задачу определения силовых факторов, действующих на летательный аппарат в ходе его наземных испытаний. Для идентификации параметров модели динамометра может использоваться описанное в статье приспособление. Точность идентификации может быть повышена за счет увеличения числа экспериментов и использования статистических методов обработки их результатов.