Teaching Partial Order Relations: A Programming Approach
Автор: Dayou Jiang
Журнал: International Journal of Education and Management Engineering @ijeme
Статья в выпуске: 1 vol.14, 2024 года.
Бесплатный доступ
This paper investigates teaching methods that leverage programming techniques to strengthen the understanding of partial ordering relations. Partial orders are vital in diverse domains, such as mathematics and economics. A comprehensive teaching framework is presented in this paper, incorporating standard programming languages to instruct partial order relations effectively. The approach integrates theoretical concepts, practical illustrations, and interactive programming exercises to enhance students' comprehension and application of partial order relations. Furthermore, the evaluation of teaching effectiveness and potential implications for computer science and mathematics education are discussed.
Discrete mathematics, partial order relations, teaching framework, Python programming, algorithm implementation
Короткий адрес: https://sciup.org/15018831
IDR: 15018831 | DOI: 10.5815/ijeme.2024.01.03
Текст научной статьи Teaching Partial Order Relations: A Programming Approach
In mathematics, particularly order theory, a partial order defines a relationship where specific pairs of elements are arranged in a precedence manner [1]. Partial order theory holds significant theoretical importance and boasts diverse practical applications. Notably, in discrete mathematics, abstract algebra, and topology, partial order structures, such as connectivity and the organization of chains and antichains, heavily rely on the concept of partial orders.
Moreover, partial orders find extensive use in algorithm design and optimization, enabling the development of efficient sorting, scheduling, and search algorithms. These applications extend to economics, where they prove valuable in analysing consumer preferences, market competition, resource allocation, and social choices. Similarly, partial orders are pivotal in algorithm design, graph theory, database query optimization, and task scheduling in computer science.
Partial order theory is vital in engineering and operations research, supporting project management, supply chain optimization, and logistics scheduling. Furthermore, partial orders have profoundly influenced social science and decision analysis, providing essential tools for multi-indicator system analysing [2], ranking, preference modelling, process mining [3], teaching model [4], and multi-criteria decision-making. Notably, the applied sciences have witnessed new theoretical and methodological developments in partial order, showcased in the book "Partial Order Concepts in Applied Sciences," [5] which explores various applications, including multidimensional poverty, economic development, inequality measurement, ecology and pollution, biology, and more.
The Study aims to enhance students' grasp of partial order relations by integrating computer programming techniques. Content includes providing programming examples to reinforce understanding and assessing the effectiveness of this approach.
The paper contributes by presenting a novel teaching framework that integrates programming techniques to enhance students' comprehension and practical application of partial order relations. This approach addresses existing gaps in the literature related to the teaching of these concepts, offering a unique and effective strategy for improving students' understanding and skills in this fundamental mathematical domain.
The paper's structure is organized as follows: Section 2 provides an overview of partial order relations, explaining their definition and properties. Section 3 presents the design of the teaching curriculum, which encompasses the selection of programming languages, the development of programming exercises, and the integration of theoretical concepts. To illustrate the practical implementation of partial order relations, Section 4 offers programming examples and code demonstrations. The teaching approach is evaluated in Section 5, including the assessment methods used to measure students' learning outcomes. Section 6 discusses the findings, highlighting the effectiveness of incorporating programming techniques and providing recommendations for future research. Finally, in Section 7, the paper concludes, emphasizing the significance of teaching partial order relations using computer programming techniques and the potential impact on students' learning experiences.
2. Overview of Partial Order Relations
Several papers have explored effective teaching methodologies in discrete mathematics education [6,7]. However, the literature appears to be limited regarding the specific topic of partial orders. While there is abundant research on various aspects of discrete mathematics, such as graph theory [8], combinatorics [9], and set theory [10], there needs to be more in teaching partial order relations.
Traditional methods often rely on theoretical explanations and visual representations to convey the concepts. These approaches emphasize the mathematical properties and definitions of partial order relations, enabling students to comprehend the formal aspects of the idea. However, they may require additional practical applications and hands-on experiences.
Alternatively, interactive and experiential learning methods have been adopted by some educators [11]. These approaches encourage active engagement with partial order relations through simulations, case studies, and group discussions. Students can grasp the practical implications and develop problem-solving skills by applying partial order relations to real-world scenarios. Nevertheless, integrating programming techniques into these teaching approaches still needs to be explored.
The integration of programming techniques in education has garnered significant attention in recent years [12,13]. Programming languages provide a practical and interactive medium for teaching abstract concepts. Students better understand theories and their computational applications through coding and algorithm implementation. Moreover, programming facilitates visualization and data analysis, enabling dynamic and interactive exploration of partial order relations. This integration enhances the learning experience by offering hands-on engagement, bridging the gap between theoretical concepts and real-world applications.
Prior research on teaching partial order relations has predominantly focused on theoretical aspects, with limited exploration of programming integration. These studies have emphasized the importance of visual aids, such as graphs and diagrams, for ex-plaining partial order relations. Additionally, interactive software tools [14] have been developed to facilitate visualization and exploration of partial order relation properties.
3. Teaching Design for Partial Order Relations
This study aims to equip students with a comprehensive understanding of partial order relations and their practical applications. The learning objectives encompass grasping the concept and properties of partial order relations, recognizing their relevance in real-world scenarios, applying them proficiently in problem-solving and decision-making, analysing them through programming techniques, and fostering critical thinking skills.
To facilitate effective teaching, a diverse range of strategies can be employed:
-
i. Interactive lectures: Engaging students with real-life examples and highlighting the practical relevance of partial order relations.
-
ii. Visual aids: Utilizing graphs, diagrams, and visualizations to enhance students' comprehension of the subject matter.
-
iii. Collaborative learning: Encouraging group discussions and peer-to-peer knowledge sharing to promote active learning.
-
iv. Case studies and simulations: Present practical scenarios for analysing and applying partial order relations.
-
v. Programming exercises: Implementing algorithms and manipulating data structures to reinforce their programming skills while deepening their understanding of partial order relations.
The selection of programming languages plays a crucial role in the teaching design for partial order relations. The choice of languages should align with the educational goals, learning objectives, and practical applications of partial order relations. Consideration should be given to popular programming languages such as C, C++, Python, and Java, which offer a wide range of libraries, frameworks, and tools for data manipulation and algorithm implementation.
By effectively integrating programming languages into the teaching design, students can gain practical programming skills and apply them to analyse and manipulate partial order relations, reinforcing their understanding and expanding their capabilities.
p. The comprehension of w concept and properties
—. The recognition of applicable v real-world scenarios
The application in problemsolving and decision-making
The analysis and
О interpretation using programming techniques
The enhancement of critical О thinking and algorithmic reasoning skills

Teaching Design for Partial Order Relations (learning objectives, pedagogical strategies and resources)
Utilizing visual aids, such as graphs, diagrams, and interactive visualizations
Introduce fundamental concepts, provide real-life examples
Encouraging students to work in Collaborative Learning — groups to discuss and solve problems j 1 v Presenting case studies and Case Studies and Simulations — . , simulations
— Programming Exercises
^Designing exercises to analyze and utilize partial order relations
Fig. 1. Teaching design for partial order relations: learning objectives, pedagogical strategies, and resources
4. Practical Examples and Code Demonstrations 4.1 Introduction to Partial Order Relations Using Programming
A relation R on a set A is called a partial order relation [15] if it is
Vx(x E A ^ (x, x) E R) = 1(1)
VxVy(x E A Л у E A Л ((x, y) E R Л (y, x) E R) ^ x = y) = 1(2)
VxVyVz(x E A Л y E A Л z E A Л (x, y) E R Л (y, z) E R ^ (x, z) E R) = 1(3)
Formulas (1) ~ (3) respectively represent reflexive relationships, antisymmetric relationships and transitive relationships.
A set P with an order relation < is said to be a partially ordered set [16].
A partially ordered set is an ordered set if for all x,y E P, then either x < y or y < x. That is, any two elements of P are directly comparable.
Practical examples and code demonstrations can be utilized to introduce students to partial order relations using programming. These examples aim to illustrate the concepts and properties of partial order relations in a hands-on and interactive manner. Students can deepen their understanding of partial order relations by observing how programming implements and manipulates these concepts.
To prepare Sichuan Mapo tofu, the following tasks need to be performed:
-
i. Cubing the tofu.
-
ii. Chop the beef into beef stuffing.
-
iii. Cutting the garlic sprouts into sections and mincing the garlic and ginger.
-
iv. Heating water in a pot, add tofu cubes and salt, cook for a while, and then remove them.
-
v. Heating oil to 70% heat, stir-frying garlic, ginger, and bean paste, adding beef stuffing, and sauteing until
fragrant.
-
vi. Adding tofu cubes, chili powder, boiling water, and garlic, and sauteing until fragrant. Plating and serving.
Students can use Python to create a program that prompts users to complete the abovementioned tasks. Data structures like dictionaries or tuples can represent partial orders, and students can learn how to visualize partial orders through code.
-
i. Create relations R based on the sequence of tasks, using (a, b) to indicate that task a must be completed
before task b. Then, R can be expressed as:
R = {(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),(1,4),(1,6),(2,5),(2,6),(3,5),(3,6),(4,6),(5,6)}
-
ii. Write Python code to visualize the partial order relations.
G = nx.DiGraph()
G.add_edges_from([(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (1, 4), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6), (4, 6), (5, 6)])
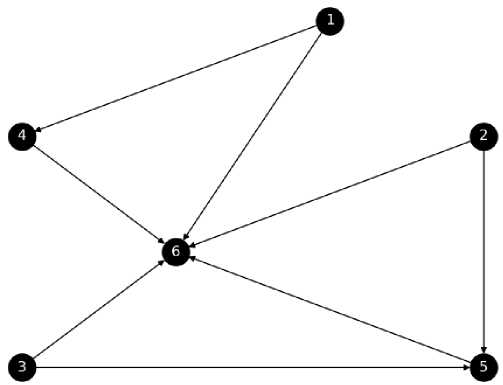
Fig. 2. Relation Diagram of Mapo Tofu making procedure.
Hasse diagram R’ is a mathematical diagram used to represent a finite partially ordered set by drawing its transitive reduction. For a partially ordered set {(5, <)}, one represents each element of S as a vertex in the plane and draws a line segment or curve that goes upward from one vertex x to another vertex y whenever y covers x. R’ meets
(x, x) e R ^ (x, x) ^ R' (4)
(x,y) e R л (y, z) e R л (x, z^ e R ^ (x,z) ^ R ' (5)
-
iii. Define HasseDiagram function:
def HasseDiagram(R):
R1=R for (u,v) in R:
if (u==v):
R1=R1-{(u,v)}
R=R1
for (x,y) in R:
for (u,v) in R:
if ((y==u) and (x,v) in R1):
R1=R1-{(x,v)} return R1
Therefore, the Hasse R’ is {(1, 4), (2, 5), (3, 5), (4, 6), (5, 6)}.
The node position is set to pos = {1: (0, 0), 2: (2, 0), 3: (4, 0), 4: (1, 1), 5: (3, 1), 6: (2, 2)}.
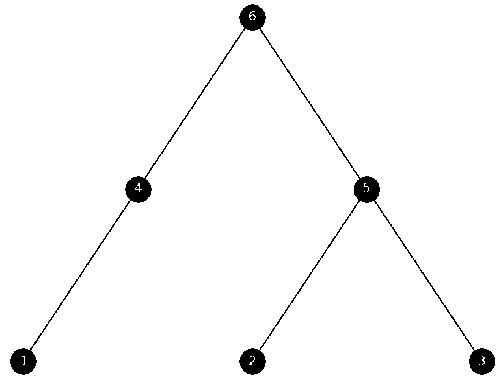
Fig. 3. Hasse diagram of Mapo tofu-making process
-
4.2 Designing and Implementing Partial Order Relations Algorithms
Expanding on the introduction, the subsequent step involves delving into designing and implementing algorithms relevant to partial order relations. The process guides students in developing algorithms that operate on partial order relations, carrying out tasks such as transitivity closure, topological sorting, or identifying maximal and minimal elements.
Python is the programming language for students to progressively implement these algorithms progressively, thereby gaining hands on experience translating theoretical concepts into practical code. The code demonstrations elucidate the algorithmic logic and illustrate how they utilize partial order relations to attain the desired outcomes.
As an illustration, an algorithm can be implemented to determine whether a given set of elements constitutes a partial order relation. Students will write Python functions that take input relations, check for reflexivity, antisymmetric, and transitivity, and produce an output indicating whether the input fulfils the properties of a partial order relation.
Let < be a partial order over set S, B is a non-empty subset of S.
An element x ∈ B is the least element of B if
3b(b E В Л Vx(x E В ^ b < x)) = 1(6)
It is the greatest element of B if
3b(b E В Л Vx(x E В ^ x < b)) = 1(7)
Let < be a partial order over set S, B is a non-empty subset of S.
An element x ∈ B is a minimal element of B if
3b(b E В Л Vx(x E В Л x < b ^ x = b)) = 1(8)
An element x ∈ B is a maximal element of B if
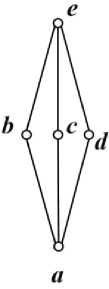
3b(b E В Л Vx(x EВЛb Let A={1,2,3,4,6,12}, < is the divisibility relation R on A. Let B1={1,2,3,4,6}, B2={4,6,12} is a subset of set A, and try to find the maximum elements, minimum elements, least elements, and greatest elements of B1 and B2. Problem-solving steps: i. Given a set A and its subset B, and solve the divisibility relation R on the subset B. a = eval(input("input set A, as list: ")) b = eval(input("input set B, as list: ")) R_B = [(i, j) for i in b for j in b if j % i == 0] Therefore, the Relation R of set B1 is expressed as R_B = (1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)] ii. Find the number of times each element in the set B is used as a predecessor and a successor. Num_i = [(sum(i == pair[0] for pair in R_B), sum(i == pair[1] for pair in R_B)) for i in b] print("The times of each element as the precursor and the latter:", Num_i) Therefore, the Num_i is [(5, 1), (3, 2), (2, 2), (1, 3), (1, 4)]. iii. Find the Least/Greatest elements of set B. S_GT = [b[i] for i in range(len(b)) if Num_i[i] == (1, len(b))] S_LT = [b[i] for i in range(len(b)) if Num_i[i] == (len(b), 1)] print("Greatest:", S_GT[0] if S_GT else "Null") print("Least:", S_LT[0] if S_LT else "Null") iv. Find the Minimal/Maximal element of set B. S_MI = [b[i] for i in range(len(b)) if Num_i[i][1] == 1] S_MA= [b[i] for i in range(len(b)) if Num_i[i][0] == 1] print("Minimal:", S_MI if S_MI else "Null") print("Maximal:", S_MA if S_MA else "Null") The Minimal/Maximal element, Least/Greatest element of B1 and B2 are shown in Table 1, Table 1. The Minimal/Maximal element, Least/Greatest element of B1 and B2 Set Greatest Least Maximal Minimal B1 = {1,2,3,4,6} Null 1 4, 6 1 B2 = {4,6,12} 12 Null 12 4, 6 Further, if the search range of the most significant and minor elements is extended to set A, then B's upper and lower bound will be obtained. A poset in which every pair of elements has a least upper and a greatest lower bound is called a lattice. There are two binary operations defined for lattices: i. Join: The join of two elements is their least upper bound. It is denoted by ⋁. ii. Meet: The meet of two elements is their greatest lower bound. It is denoted by ⋀. Determine whether the partially ordered set corresponding to the Hasse diagram shown in Fig. 4 is a lattice. Fig. 4. The partially ordered sets i. Extract all elements in the set to which the relations belong. elements = set(x for pair in rel for x in pair) ii. Judge the relations' reflexivity, anti-symmetry, and transitivity. for x, y in rel: if x == y or (y, x) not in rel: continue else: return False for x in elements: for y in elements: for z in elements: if (x, y) in rel and (y, z) in rel: if (x, z) not in rel: return False iii. Determine if any two elements have the greatest lower and smallest upper bound to identify a lattice. for x in elements: for y in elements: if (x, y) not in rel and (y, x) not in rel: has_sup = False hasinf = False for z in elements: if (x, z) in rel and (y, z) in rel: hassup = True if (z, x) in rel and (z, y) in rel: has inf= True if not (has_sup and hasinf): return False The relations and element sets of two graphs are represented according to the Hasse diagram as follows: Left Graph: R={(’a’, 'a'),('b', 'bf('c', 'cf'd', 'd'),('e', 'e'),('f,'f),('a', 'b'),('a', 'bf('a', ’d), ('a', 'e),('aVf),Cb'' 'd),('b'' b;’)^'!)’,^^^’, 'd),('c'' 'e'fCcfffCd', 'e'),('dVf)}, P={'a', 'b\ ’c’, W, 'eff) Right Graph: R={(a', 'a),('b', 'b),(C', 'c),(d, 'd),('e', e ),('a', 'b ffa', C'),('a','d),fa', 'e),fb', 'e'),Cc', 'e'),('d'. 'e')}, P={'a', b'', C', d , 'e} Both graphs can be classified as partially ordered sets. However, in the left diagram, there is no least upper bound within the group {'e', 'f'}. Conversely, in the right diagram, any two poset elements have the least upper and greatest lower bound. Consequently, the left graph does not satisfy the conditions of a lattice, while the right graph does.
5. Evaluation and Learning Outcomes Assessing the effectiveness of teaching partial order relations using programming techniques requires appropriate assessment methods and metrics. These can include knowledge tests to evaluate theoretical understanding, programming assignments to assess practical application skills, project-based assessments to analyse real-world scenarios, and peer evaluation/group projects to promote collaboration and feedback. Project-based Assessment This allows students to demonstrate their ability to apply partial order relations to relevant applications, effectively utilize programming tools, and comprehensively present their findings. Programming Assignments This can evaluate students' programming skills by requiring them to implement algorithms, manipulate data structures, and solve problems related to partial order relations using Python. Peer Evaluation and Group Projects Peer and group projects foster collaborative learning and enable students to assess each other's understanding and implementation of partial order relations. Fig. 5. Assessment methods and metrics. The assessment results can be analysed quantitatively by calculating scores or grades and qualitatively by reviewing solutions, code implementations, and project reports. This analysis provides insights into overall performance, problem-solving approaches, interpretation of partial order relations, programming proficiency, and identifying areas for improvement or common misconceptions. Analysing learning outcomes helps identify strengths and weaknesses in the teaching approach, enabling instructional improvements and tailored interventions for individual students. Discussions should focus on the effectiveness of incorporating programming techniques, including the impact on engagement, motivation, and understanding. Student feedback can provide valuable insights for enhancing the teaching approach and exploring the transferability of skills to other domains.
6. Discussion and Conclusion The study's findings reveal that students' understanding of theoretical concepts and ability to apply them in practical scenarios are enhanced by integrating programming techniques in teaching partial order relations. The hands-on approach and interactive learning experiences fostered engagement and motivation among students. Improved programming skills, critical thinking abilities, and problem-solving proficiency are demonstrated by analysing learning outcomes and student performance. Further investigation into the impact of different programming languages, frameworks, or tools on the teaching and learning experience would be valuable. Different languages may have varying levels of complexity, readability, and applicability to certain mathematical concepts. Evaluating the strengths and weaknesses of each language in this context could guide educators in selecting the most suitable language for teaching partial order relations. Additionally, future research could focus on evaluating the long-term retention of knowledge and skills acquired through the teaching approach and assessing the transferability of these skills to other domains. Are students better equipped to tackle interdisciplinary problems, and do they find it easier to adapt their skills to novel contexts? Answering these questions would elucidate the broader implications of this teaching approach. In summary, this research has undertaken a comprehensive exploration of teaching partial order relations through the integration of programming techniques. A teaching framework was designed, incorporating interactive lectures, visual aids, collaborative learning, case studies, simulations, and programming exercises. The choice of programming languages aligned with educational goals, providing a diverse and effective set of tools for conveying abstract concepts. Implementing practical examples using Python illustrated how programming can be seamlessly integrated into teaching partial order relations. Students were guided through hands-on exercises, visualizing relations, and applying algorithms, thereby reinforcing their understanding through practical application. In conclusion, teaching partial order relations using programming techniques offers a promising approach to enhancing students' understanding and application of this fundamental mathematical concept. Integrating programming languages like Python facilitates hands-on learning, promotes critical thinking, and strengthens problem-solving abilities.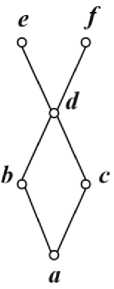

Список литературы Teaching Partial Order Relations: A Programming Approach
- https://en.wikipedia.org/wiki/Partially_ordered_set
- Carlsen, L., & Bruggemann, R. (2021). Inequalities in the European Union—A Partial Order Analysis of the Main Indicators. Sustainability, 13(11), 6278.
- Leemans, S.J.J., van Zelst, S.J. & Lu, X. (2023). Partial-order-based process mining: a survey and outlook. Knowl Inf Syst. 65, 1–29.
- Gao, Z., Ries, C., Simon, H., & Zilles, S. (2016). Preference-based teaching. In Conference on Learning Theory, Hamilton, New Zealand, November 16-18, 971-997.
- Fattore, M., & Bruggemann, R. (2017). Partial order concepts in applied sciences. Cham: Springer International Publishing.
- Hart, E. W., & Sandefur, J. (2017). Teaching and learning discrete mathematics worldwide: Curriculum and research. Springer.
- Ouvrier-Buffet, C. (2020). Discrete mathematics teaching and learning. In Encyclopedia of mathematics education. Cham: Springer International Publishing. 227-233.
- Heckmann, T., Schwanghart, W., & Phillips, J. D. (2015). Graph theory—Recent developments of its application in geomorphology. Geomorphology. 243, 130-146.
- Shevtsova, M., Kanel-Belov, A., & Golafshan, M. (2023). An Indirect Method for Solving Combinatorial Problems. arXiv preprint arXiv:2302.09761.
- Kaplansky, I. (2020). Set theory and metric spaces. American Mathematical Society. Vol. 298.
- Bradford, M., Muntean, C., & Pathak, P. (2014). An analysis of flip-classroom pedagogy in first year undergraduate mathematics for computing. In 2014 IEEE Frontiers in Education Conference (FIE) Proceedings, Madrid, Spain, October 22-25, 1-5.
- McMaster, K., Anderson, N., & Rague, B. (2007). Discrete math with programming: better together. ACM SIGCSE Bulletin. 39(1), 100-104.
- Liu, Y. A., & Castellana, M. (2021). Discrete math with programming: A principled approach. In Proceedings of the 52nd ACM Technical Symposium on Computer Science Education, Virtual Event USA March. 13 – 20,1156-1162.
- Brüggemann, R., Carlsen, L., Voigt, K., & Wieland, R. (2014). PyHasse software for partial order analysis: Scientific background and description of selected modules. Multi-indicator systems and modelling in partial order. 389-423.
- O'Regan, G. (2021). Guide to discrete mathematics. Springer International Publishing.
- Fuchs, L. (2011). Partially ordered algebraic systems, Courier Corporation. Vol. 28.


