Течение Гартмана в слое жидкости с пространственно неоднородными свойствами

Магнитное поле оказывает существенное воздействие на течения проводящих сред. Классическим примером изменения профиля скорости потока под действием магнитного поля является задача Гартмана о течении проводящей жидкости между параллельными плоскостями, перпендикулярно которым наложено магнитное поле [1]. Важно, что магнитное поле не только уплощает профиль скорости, концентрируя вязкие напряжения в пограничных слоях, которые становятся все уже по мере роста магнитного поля, но и существенно сдвигает порог устойчивости, что было обнаружено в первом же экспериментальном исследовании течения ртути в поперечном магнитном поле [2]. Систематические исследования зависимости границы устойчивости при течении ртути в каналах прямоугольного сечения в поперечном магнитном поле показали, что критическое число Рейнольдса Re * ( Re = Uh / v, где U - средняя скорость потока, h - полуширина слоя, а v - кинематическая вязкость жидкости) растет линейно с ростом числа Гартмана ( Ha = Bh^ о / п , где B - индукция наложенного магнитного поля, о - электрическая проводимость, п - динамическая вязкость жидкости), то есть Re/ Ha = C , и константа C при увеличении отношения размера канала поперек поля к размеру вдоль поля (то есть при приближении к случаю неограниченного слоя) C ~ 215 [3]. Отметим, что число Рейнольдса, отнесенное к числу Гартмана, является, по сути, числом Рейнольдса, в котором в качестве масштаба использована толщина гартмановского пограничного слоя. Таким образом, полученный результат означает, что устойчивость всего течения определяется устойчивостью пограничного слоя.

Дальнейшие эксперименты с различными металлами и каналами, выполненные в различных диапазонах значений индукции магнитного поля, позволили принять, что для широкого класса течений и Ha > 20 можно пользоваться оценкой 200 < C < 400 [4, 5]. Эта оценка указывает на то, что в сильных магнитных полях течения металла могут оставаться ламинарными даже при очень больших значениях числа Рейнольдса. Так, в проектируемых жидкометаллических элементах охлаждения токамаков ожидаемые числа Гартмана достигают 104, что сдвигает границу устойчивости до Re-106 и выше. Однако именно исследования течений жидкого металла в контексте возможности их использования в охлаждающих системах термоядерных установок показали, что влияние магнитного поля не столь однозначно и в течениях с большими перепадами температуры возникают пульсации температуры (и скорости), значительно превосходящие даже те, что могли бы быть в отсутствие магнитного поля [6, 7]. Так, в случае опускного течения ртути в подогреваемом с одной стороны вертикальном канале колебания температуры при сильном нагреве подавляются только при Ha > Re/10 [8], то есть для ламинаризации потока магнитное поле должно быть на порядок сильнее, чем в отсутствие нагрева. Эти пульсации температуры получили название магнитоконвективных, и их возникновение было объяснено тем, что в результате действия электромагнитных сил и сил плавучести происходит трансформация профиля скорости, в котором появляются точки перегиба, способствующие развитию неустойчивости (см. обзор [5]).

Цель данной работы состоит в том, чтобы выяснить, насколько неоднородности свойств жидкого металла в слое могут исказить гартмановский профиль скорости и могут ли эти искажения сопровождаться появлением точек перегиба. Точки перегиба не являются достаточным условием возникновения неустойчивости, но могут способствовать ей. Ниже будет рассмотрена стандартная задача Гартмана о течении жидкости в поперечном магнитном поле с учетом возможных вариаций проводимости и вязкости жидкости поперек слоя.

Неоднородность свойств жидкости может быть вызвана, к примеру, вариациями температуры или наличием примесей. В данной работе вопрос о причинах возникновения неоднородности не обсуждается и не рассматриваются эффекты, связанные с изменением плотности и появлением сил плавучести. Это сделано сознательно, чтобы разобраться с изолированным эффектом. Однако стоит отметить, что мотивацией для изучения этой задачи послужили разработки различных систем МГД-перемешивания [9, 10] и МГД-сепарации металлов с примесями [11, 12], в которых возникают потребности как в интенсификации перемешивания потока в магнитном поле (турбулизации потока в режимах, когда он остается ламинарным под действием поля), так и, наоборот, в подавлении интенсивного перемешивания примеси.

Задача Гартмана

Рассматривается одномерное течение жидкости v = {V ( z ),0,0 } в плоском слое, ограниченном двумя параллельными плоскостями, находящимися на расстоянии 2 h друг от друга в поперечном магнитном поле B = B e z (рис. 1). Движение жидкости вызвано перепадом давления, имеющим заданный градиент V p .

В отсутствие внешнего электрического поля выражение для электромагнитной силы принимает вид

F ^em = j x B = c B ² ( v x e _z ) x e _z ,

что позволяет записать безразмерные уравнения Навье–Стокса для несжимаемой жидкости в виде dv    „   „     1      Ha2 /     x     „

--+ v -V v = P e_v +--A v +---- ( v x e₇ ) x e₇ , V- v = 0 .

St              x Re      Re ^v     z⁷ z

В качестве единиц измерения длины, скорости, времени, давления и индукции магнитного поля выбраны соответственно величины h , U , h / U , р U ² и B , где U - средняя скорость течения, р - плотность жидкости. В уравнения входят безразмерный приложенный градиент давления P и два безразмерных параметра - число Гартмана

Ha = Bh^/n ,                                (3)

квадрат которого определяет отношение электромагнитных сил к силам вязкости и число Рейнольдса

Re = UP

П

.

Механика

Рис. 1. Задача Гартмана с характерным профилем скорости для однородной среды

В стационарном случае задача (2) сводится к обыкновенному дифференциальному уравнению

V " = - Re P + Ha ² V .                               (5)

Здесь штрихом сверху обозначена производная по координате z . Решение этого уравнения с учетом граничных условий V ( -1 ) = V ( 1 ) = 0 было получено Гартманом [1] и имеет вид

V ( z ) =

Re P ( ch ( Ha z )² Ha² ( ch ( Ha ) ,

Интегрирование этого решения с учетом нормировки расхода

J V ⁽ z ) dz = 1

² - 1

позволяет избавиться от градиента давления и дает окончательный профиль скорости в виде ch (Haz)

1--;----^ , ch (Ha) J

v ( z ) = —Ha—-^v ’ Ha - th ( Ha )

откуда следует, что число Рейнольдса не влияет на профиль скорости.

Неоднородное распределение свойств жидкости

Неоднородность свойств жидкости (конкретно, вязкости и проводимости) поперек слоя может существенно влиять на профиль скорости течения. Неоднородность может быть вызвана, к примеру, вариациями температуры или наличием примесей. В данной работе вопрос о причинах возникновения неоднородности не обсуждается, но рассматриваются эффекты, которые такая неоднородность может вызвать.

В случае пространственно неоднородных вязкости и проводимости уравнение Навье–Стокса (2) перепишется в виде

• — + v -V v = P e + —— ^A v + —— V^-V v + ф a ⁰ ( v x e ) x e .            (9)

d t              x  Re₀       Re₀            Re₀^V     z’ z

Здесь ^ = n ( r ) / П о и Ф = ^ ( г ) / ст₀ - безразмерные вязкость и проводимость соответственно, а нижний индекс у чисел Гартмана и Рейнольдса означает, что они определяются по средней проводимости о₀ и средней вязкости р₀.

Уравнение для определения стационарного профиля скорости в задаче Гартмана с учетом неоднородных свойств жидкости запишется в виде

• V " = -Reo P + Ha2 Й) v - d M v '.                     (10)

^       ⁰ UJ     dz

Для решения уравнения (10) необходимо задать вид распределений свойств жидкости поперек потока ^(z) и ф(z). Одним из наиболее простых вариантов неоднородного распределения свойств в потоке является линейная зависимость проводимости и вязкости от поперечной координаты. Выберем эту зависимость в таком виде, что при z = 0 значения обеих характеристик совпадают со средними значениями

Ф ( z ) = 1 + k _с z , ^ ( z ) = 1 + к _п z .

Параметры ko и kп характеризуют степень отклонения соответствующей величины от ее сред него значения. К примеру, при kп = 0,1 вязкость вблизи верхней стенки канала будет на 10 % больше среднего значения, а вблизи нижней стенки – на 10 % меньше.

При подстановке (11) и (12) в (10) получим

V ' = - Ze o Z + _На 2 Г X+bz J v ^kJ\_ v •.                  (13)

• 1    + kn z      ^ 1 + kn z J    1 + kn z

В силу симметрии (уравнение инвариантно к преобразованию { z ^- z , k_а ^- k_а , k _n ^- k _п } ) достаточно рассмотреть лишь положительные значения одного из параметров, а профили скорости для отрицательных значений этого параметра можно получить отражением относительно оси z = 0.

На рис. 2 приведены профили скорости для значений среднего числа Гартмана 5 и 25. При отсутствии неоднородности проводимости жидкости (случай a) отклонение от обычного гартма-новского профиля определяется неоднородностью вязкости. С локальным увеличением числа Гартмана градиенты скорости в ядре течения уменьшаются, в связи с чем уменьшается влияние неоднородности вязкости на профиль скорости, и поэтому отклонения от профиля течения однородной жидкости оказываются заметными лишь в пограничных слоях.

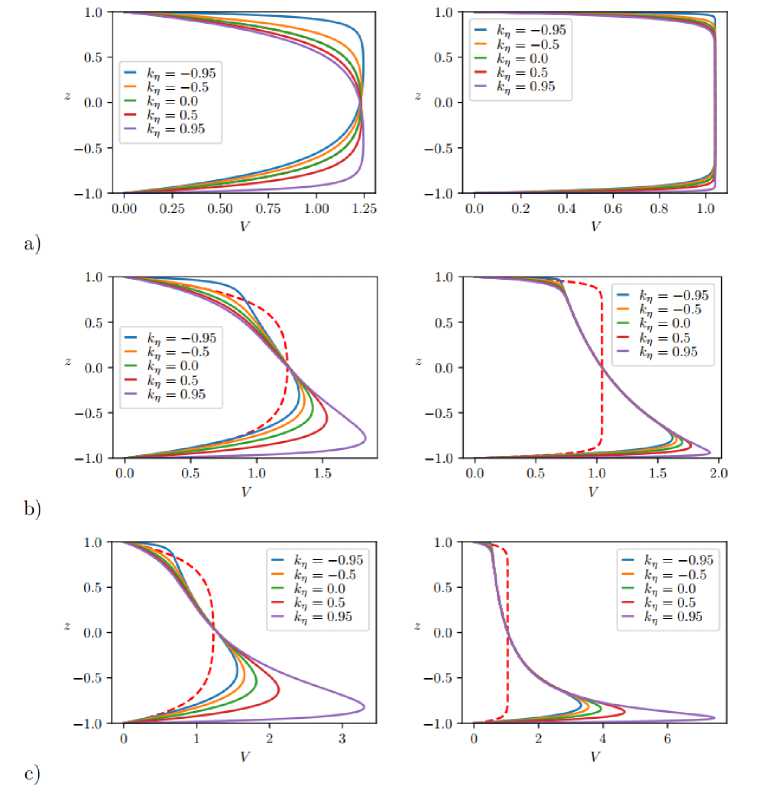
Рис. 2. Профили скорости при Ha = 5 (слева) и Ha = 25 (справа); a) k _CT = 0 , b) k _CT = 0,5 , c) k _CT = 0,95 ; красной пунктирной линией обозначен профиль скорости для течения Гартмана в случае жидкости с однородными свойствами

Представленные профили иллюстрируют появление несимметрии течения относительно центра канала. В качестве количественной характеристики отклонения от симметрии можно выбрать отношение расходов в верхней и нижней половинах канала

Механика

∫ V ( z ) dz

Q = ⁰₀         ,                                           (14)

∫ V ( z ) dz

- 1

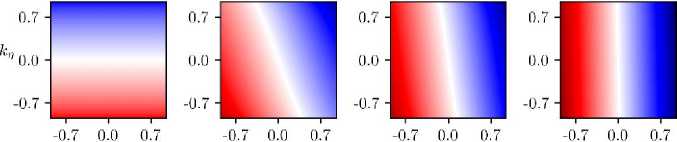
распределение которого на плоскости параметров ( k _а , k _п ) для различных значений числа Гартмана представлено на рис. 3. Белая линия на этих распределениях соответствует симметрии профиля скорости относительно центра канала. Показательными являются два предельных случая. В отсутствие внешнего поля неоднородность проводимости, очевидно, никак не влияет на течение жидкости и искажение профиля скорости определяется лишь неоднородностью вязкости. Напротив, при течении в сильном магнитном поле электромагнитные силы существенно превосходят вязкие силы и несимметрия профиля определяется неоднородностью электропроводности и практически не зависит от вязкости.

Над = 0            Нао = 5            Нао = Ю           Над = 50

кп                    кп                    ka                    к„

1.8

0.55

0.25

Рис. 3. Распределение относительного расхода Q на плоскости параметров неоднородности свойств жидкости ( k _σ , k _η ) при различных значениях среднего числа Гартмана. Цветовая шкала представлена в логарифмическом масштабе

Важной особенностью полученных профилей является появление точек перегиба, начиная с некоторых значений параметров, характеризующих неоднородность свойств. На рис. 4 показан пример для небольшого значения магнитного поля ( Ha = 5 ), при котором точки перегиба возникают только при значительной неоднородности проводимости среды. При малых Ha существует диапазон значений параметров к_о и к _п, в рамках которого точки перегиба в профиле скорости не появляются. С увеличением Ha этот диапазон существенно снижается и при Ha ≈ 10 точки перегиба появляются при любых значениях параметров. Рис. 5 иллюстрирует рост второй производной с ростом параметра неоднородности k _η (левая панель), справа представлены границы появления точек перегиба на плоскости параметров ( k , k _η ).

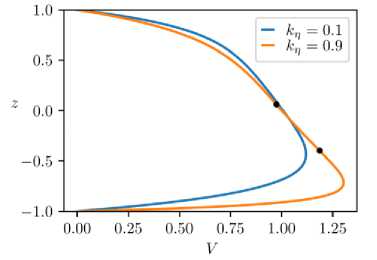
Рис. 4. Профили скорости при различных значениях параметра неоднородности вязкости, Ha = 5 , k _σ = 0,4 : синим цветом показан профиль без точек перегиба, оранжевый профиль имеет две точки перегиба (на профиле обозначены черными точками)

Очевидно, что существуют распределения неоднородности свойств жидкости, при которых точки перегиба получаются при сколь угодно малых Ha и любых ненулевых значениях параметров распределения. Такие неоднородности возникают при локальном изменении свойств во

Окатьев Р.С., Фрик П.Г., Течение Гартмана в слое жидкости Колесниченко И.В. с пространственно неоднородными свойствами внутренней точке потока. На практике такая ситуация наиболее интересна, так как возникает при впрыске примеси или локальном нагреве жидкости. Простейшей моделью локального изменения свойств может быть гауссово возмущение вида

ф ( z ) = 1 + k ^ exp { -3 z 2 } , ^ ( z ) = 1 + k _n exp { -3 z 2 } , (15)

где 3 характеризует ширину локализации неоднородности. Профили скорости, соответствующие такому распределению, всегда имеют точки перегиба (рис. 6).

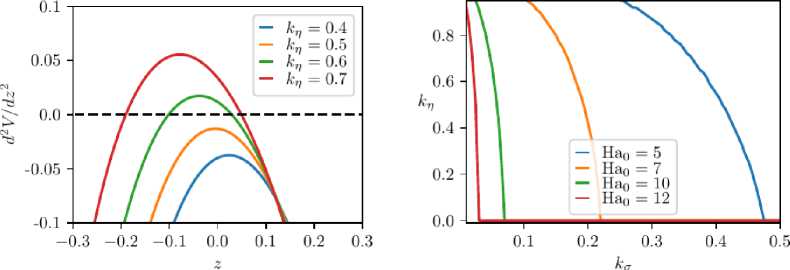
Рис. 5. Вторая производная профиля скорости при различных значениях параметра неоднородности вязкости для Ha0 = 5 и кс = 0,4 (слева) и нейтральные кривые, характеризующие появление точек перегиба в профиле скорости, на плоскости параметров (k^ , кп ) (справа)

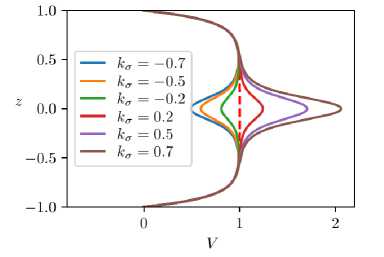
Рис. 6. Профили скорости с гауссовым распределением неоднородности свойств, к _п = 0,1 , Ha₀ = 10

Обсуждение и выводы

Рассмотрено влияние неоднородности свойств проводящей жидкости поперек слоя на формирующийся в магнитном поле профиль скорости несжимаемой жидкости. Показано, что даже небольшие неоднородности электропроводности и вязкости могут приводить к существенной трансформации гартмановского профиля скорости, причем, даже простейшее линейное распределение характеристик жидкости поперек слоя может приводить к формированию профиля скорости с точками перегиба. Для линейной зависимости вязкости и электропроводности от поперечной координаты построена граница появления точек перегиба на плоскости параметров, определяющих максимальное отклонение обеих величин от среднего значения.

Представляет интерес оценка, насколько значимы должны быть вариации свойств жидкости, чтобы обсуждаемые эффекты стали заметны. Для определенности рассмотрим поток жидкого натрия при средней температуре 200 °C. При такой температуре проводимость жидкого натрия составляет 7,81 МСм/м, а динамическая вязкость 4,52∙10–4 кг/м∙с. Примем для определенности, что ширина канала, по которому течет жидкость, составляет 10 см, и оценим перепады температуры поперек слоя, которые могут привести к появлению в профиле скорости точек перегиба. Для этого воспользуемся рис. 5 и проведем оценки для соответствующих значений числа Гартмана. Результаты оценок показаны в таблице, в которой представлены значения индукции магнитного поля, обеспечивающие в таком потоке соответствующие числа Гартмана, значения вариации проводимости, обеспечивающие появление точек перегиба и значения температуры на границах слоя, которые приведут к соответствующей вариации проводимости. По рис. 5 видно, что влияние вариаций вязкости в этом случае слабое и его можно не учитывать. Видно, что в

Механика сильных магнитных полях эффект достигается при достаточно скромных перепадах температуры (при поле порядка 2 мТл точки перегиба возникают при разности температуры порядка 20 °C). Последняя колонка в таблице дает значение объемной доли непроводящей примеси, которая обеспечивает необходимую вариацию проводимости. Для последней оценки использована модель для эффективной проводимости среды с непроводящими частицами [13]

о

e

2 - 2ф

2 + ф

^о о ,

где ф - объемная доля непроводящих частиц. Приведенные оценки показывают, что при полях порядка 2 мТл для появления точек перегиба достаточно объемной доли примеси около 2 %.

Оценки характерных значений параметров для жидкого натрия

Ha0	B , мТл	k о	T - , °C	T + , °C	* ф
7	1,0	0,22	130÷140	290÷300	0,158
10	1,5	0,07	180÷190	230÷240	0,048
12	1,8	0,025	190	210	0,017

Таким образом, точки перегиба в профиле скорости могут возникнуть при относительно небольших вариациях свойств проводящей жидкости даже при линейном распределении поперек слоя, а локализованные неоднородности (например гауссовы) всегда дают точки перегиба. Однако остается открытым важный вопрос о достаточном условии неустойчивости, то есть вопрос о реальной границе устойчивости таких течений. Ответ на него требует прямого численного решения полной системы уравнений либо лабораторных экспериментов.

Исследование выполнено за счет гранта Российского научного фонда и Пермского края № 22-19-20106,