Течение многокомпонентной смеси в желудке и двенадцатиперстной кишке с учетом функциональных нарушений: результаты численного моделирования для определения кислотности

Повышенная кислотность в желудочно-кишечном тракте может приводить к эрозивным эффектам на эмали и дентине зубов [20, 66] и к образованию язв в желудке и двенадцатиперстной кишке [44, 57] . Чаще всего язвообразование наблюдается в антродуоденуме [1, 10] , т.е. в антруме (нижнем отделе желудка, расположенном ближе к кишечнику) и в дуоденуме (двенадцатиперстной кишке).

Традиционными подходами к определению кислотности в желудочно-кишечном тракте являются экспериментальные методы. В 50–70-х гг. прошлого столетия во всем мире активно велись разработки беспроводной радиокапсулы, позволяющей определять различные характеристики среды в пищеварительном тракте, в том числе давление, температуру [49] и уровень pH [2] . Тем не менее данный метод имел ряд недостатков, связанных с невозможностью управления капсулой, сложностью определения места ее нахождения в тракте и невозможностью сопутствующего забора гистологического материала. В этой связи использование радиокапсулы ограничилось только научными целями без широкого внедрения в медицинскую практику, исключением являются pH-капсулы для диагностики гастроэзофагеальной рефлюксной болезни (заболеваний пищевода) [50] . Исследования в данном направлении возобновились в нашем веке [16, 21, 35, 40, 55, 67] , в частности, разрабатываются и внедряются в практику видеокапсулы для эндоскопии тонкого и толстого кишечника [3] , помогающие диагностировать болезнь Крона и некоторые другие заболевания пищеварительного тракта. Следует отметить перспективность применения радиокапсульных технологий для идентификации и верификации математических моделей течения среды в желудочно-кишечном тракте в случае преодоления упомянутых выше недостатков, так как несомненным преимуществом капсулы являются ее небольшой размер и, как следствие, малое влияние на изучаемые процессы.

Наиболее достоверным методом измерения кислотности в пищеводе, желудке и дуоденуме является pH-метрия, в основе которой лежит введение через нос или рот пациента pH-зонда, представляющего собой трубку с проводом [60] . Зонд передает электрические сигналы на регистрирующее устройство, записывающее результаты измерений уровня кислотности в нескольких точках желудочно-кишечного тракта. Другим вариантом измерений является откачка порций содержимого тракта для последующего анализа [15] . Помимо измерения концентрации кислоты, кратковременная pH-метрия позволяет определить функциональные возможности желудка и дуоденума по секреции и нейтрализации кислоты, для этого используются стимуляция гормонами и щелочные нагрузочные тесты [27, 53] . Cуточная pH-метрия применяется для более длительных исследований [26, 56] : пациент в течение 24 часов носит зонд с регистрирующим прибором, который позволяет определить кислотность среды в желудочно-кишечном тракте на различных стадиях пищеварения в привычных повседневных условиях. К недостаткам метода относится ограниченное количество точек замера, сложность определения точных мест забора анализа, а также физические и психологические неудобства обследуемого. Кроме того, само наличие инородного предмета в полости тракта способно исказить результаты измерений.

Помимо непосредственных методов измерения кислотности в желудочнокишечном тракте, существуют косвенные неинвазивные методы, например, дыхательные тесты [17, 58] . Однако неинвазивные методы не дают точных количественных оценок, что ограничивает их практическое использование [27] .

К общим недостаткам экспериментальных методов измерения кислотности в тракте относятся значительная погрешность измерения, существенные временные и трудовые затраты, сложность замера в реальных условиях при различных режимах потребления пищи. В этой связи целесообразно применять математические подходы для оценки и прогнозирования уровня pH в желудочно-кишечном тракте, которые обладают рядом преимуществ: существенная экономия материальных ресурсов, возможность легкого управления и быстрого прогнозирования, включения/выключения отдельных факторов. Кроме того, использование моделей на основе дифференциальных уравнений в частных производных позволяет оценивать и прогнозировать кислотность в любой точке области моделирования.

С развитием электронно-вычислительных мощностей и методов диагностики, позволяющих получать снимки внутренних органов с высоким разрешением, развиваются модели CFD ( Computational Fluid Dynamics ) для описания процессов течения жидкости со сложной реологией в разветвленных биоканалах различной формы и кривизны [41] . Тем не менее применительно к пищеварительной системе потенциал использования подходов математики и механики раскрыт не в полной мере. Одни из первых моделей для описания течения в пищеводе [45] , желудке [52] и кишечнике [34] разработаны около 15–20 лет назад. В работах последних лет, посвященных трехмерному моделированию течения в замкнутом желудке, численно исследовано влияние вязкости жидкости [23] , плотности и объемной доли частиц второй фазы [68] на характеристики процесса течения, намечены пути дальнейшего развития моделей – учет секреции желудочного сока и его взаимодействия с пищей [24] . В работах по двумерному моделированию течения в желудке рассмотрено распространение фермента пепсина в антральном отделе [39] , двухфазное течение с учетом эвакуации в кишечник [28] . Модели пищеварения в кишечнике ограничены 1D- и 2D-постановками, но более глубоки по содержанию, например, позволяют учитывать биохимические реакции [63] . Тем не менее исследователями преимущественно рассматриваются только моторика тракта, течение однофазной неньютоновской жидкости [18, 25, 46, 48, 59] . Таким образом, количество трехмерных моделей, описывающих индивидуальное строение желудочно-кишечного тракта, довольно ограничено. В указанных работах не рассматриваются кислотность содержимого тракта, биохимические реакции, секреция пищеварительных желез и растворение пищи. Кроме того, не используются особенности пищеварительных процессов при наличии патологий.

Между тем ненормативный уровень кислотности в тракте, обусловленный, в том числе, недостаточным уровнем секреции щелочи для нейтрализации соляной кислоты, может вызывать повреждения слизистой оболочки тракта и существенно влиять на пищеварительные процессы. Например, в экспериментах показано, что внутривенное введение гидрокарбонатов способствует уменьшению вероятности образования язвы у крыс при остром воздействии HCl, а введение веществ, блокирующих выработку щелочи, приводит к увеличению вероятности язвообразования [61] . В экспериментальных исследованиях обнаружено, что при перфузии через дуоденум свиньи в течение 15 минут раствора соляной кислоты концентрацией 0,03 и 0,1 моль/л (pH = 1,5 и pH = 1) поражается 16 и 57 % площади слизистой оболочки соответственно [14] . Кроме того, в этой же работе показано, что при внутривенном введении вазоактивного интестинального пептида, стимулирующего секрецию гидрокарбонатов слизистой оболочкой, поражается только 7 % площади слизистой при воздействии соляной концентрацией 0,03 моль/л.

В силу того что организм человека представляет собой набор сложных биологических систем с наличием множества взаимосвязей, при разработке подходов для описания отдельных органов и систем необходимо стремиться к учету взаимодействий с другими системами. Указанное положение соответствует принципам фундаментальной концепции международного проекта Physiome, посвященного проблемам описания физиологии всего организма человека [7, 31]. Для описания процессов накопления повреждений в органах и системах под воздействием факторов различной природы коллективом исследователей, в том числе авторами данной статьи, разрабатывается многоуровневая математическая модель [12]. На верхнем уровне модели описывается осредненное взаимодействие систем организма между собой. На мезоуровне (уровне органа) более детально рассматриваются повреждения участков антродуоденума под воздействием химических веществ, в том числе соляной кислоты из полости тракта. Предложена математическая модель для описания течения многофазной многокомпонентной смеси в трехмерном антродуоденуме с учетом нарушений основных функций, наличия массовых источников за счет межфазного обмена, секреции и всасывания компонент смеси, в численных экспериментах исследовано влияние функциональных нарушений и свойств фаз, описывающих пищу, на характеристики процесса течения [64].

Разработанная модель для описания течения смеси в антродуоденуме позволяет определять массовые концентрации компонент смеси, в том числе соляной и угольной кислот, гидрокарбоната натрия. Для идентификации и верификации получаемых результатов, оценок степени повреждения слизистой оболочки тракта встает задача определения уровня pH смеси, так как именно этот показатель используется в экспериментах. Взаимодействие соляной кислоты и гидрокарбонатов в желудочнокишечном тракте осуществляется на молекулярном уровне, при этом в избытке остается либо смесь соляной и угольной кислот, либо угольной кислоты и гидрокарбонатов. Приближенные формулы для расчета уровня pH в зависимости от концентрации компонент дают значительные погрешности при малых концентрациях. В этой связи целесообразно разработать подходы, позволяющие получать более точные решения. Таким образом, статья посвящена проблемам развития математической модели антродуоденума для определения кислотности смеси в полости тракта. В данной работе детально изложены материалы для численного исследования распределения уровня pH в антродуоденуме в зависимости от наличия функциональных нарушений.

Концептуальная постановка

Рассматривается стадия пищеварения, когда содержимое желудка начинает переходить в кишечник, при этом температура смеси в желудке достигла температуры тела человека. Исследуемые процессы в первом приближении полагаются изотермическими. Так как в данной работе основное внимание уделено определению уровня pH в тракте, чтобы дополнительно не перегружать текст статьи, сделано существенное упрощение разработанной модели. Рассматривается течение однофазной многокомпонентной жидкости в антродуоденуме с растворенными на молекулярном уровне компонентами (индекс i = 0, I ): соляной кислотой ( i = 0), продуктом реакции соляной кислоты и гидрокарбоната натрия (углекислым газом и хлоридом натрия) ( i = 1), гидрокарбонатом натрия ( i =2), водой ( i =3).

В модели учитывается реакция нейтрализации между соляной кислотой (HCl) и гидрокарбонатом натрия ( NaHCO ), в результате реакции образуется хлорид натрия NaCl и угольная кислота H CO , которая может разлагаться на воду HO и диоксид углерода CO . Продукт реакции предполагается состоящим из двух компонент – воды и смеси хлорида натрия и диоксида углерода, которые растворены на молекулярном уровне. Для описания химической реакции в уравнениях сохранения массы вводятся массовые источники для компонент смеси. В силу малых концентраций взаимодействующих веществ тепловой эффект реакции не учитывается.

В антродуоденуме осуществляется секреция соляной кислоты и гидрокарбоната натрия. Секреторные процессы описываются с помощью объемных массовых источников вблизи границы области моделирования (стенки тракта). Так как в данной постановке компоненты пищи в смеси отсутствуют, интенсивность массовых источников кислоты постоянна и не зависит ни от каких факторов. При описании секреции гидрокарбоната натрия учитывается функциональность по передаче управляющего сигнала через нейроэндокринные механизмы. Предполагается, что рецепторы определяют уровень кислотности в теле желудке и передают команды на изменение интенсивности массового источника гидрокарбоната натрия в антродуоденуме.

На рассматриваемой стадии пищеварения для антрума характерно распространение перистальтических волн по направлению к кишечнику со значительной степенью сжатия мышц стенки (амплитудой). В модели предполагается, что моторика антродуоденума является периодической, учитываются перистальтические волны в антруме, дуоденуме, а также сокращение/сжатие пилорического сфинктера. Параметры волнового процесса полагаются не зависящими от свойств содержимого тракта.

На основе консультаций со специалистами граница области моделирования разбита на несколько подобластей по функциональному и геометрическому признаку [64] (рис. 1). В области тела желудка ∂Ω вводятся массовые источники соляной кислоты. В нижней части желудка (в антруме) ∂Ω , примыкающей к области пилорического отверстия, секретируется гидрокарбонат натрия. В области пилорического отверстия и двенадцатиперстной кишки ∂Ω также введены массовые источники гидрокарбоната натрия. В центральной части двенадцатиперстной кишки выделена зона ∂Ω , которая имитирует место выхода протоков от поджелудочной железы и печени, секреты которых также содержат гидрокарбонат натрия. ∂Ω , ∂Ω представляют собой входную и выходную границы исследуемой области,

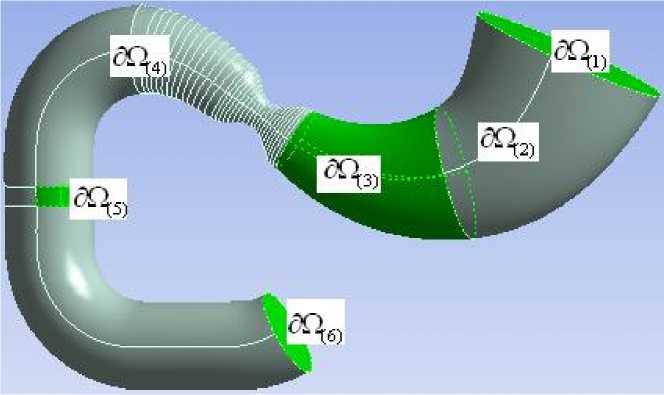
Рис. 1. Выделение подобластей по функциональному и геометрическому признаку: ∂Ω – зона секреции кислоты; ∂Ω , ∂Ω , ∂Ω – зоны секреции гидрокарбоната натрия; ∂Ω , ∂Ω – сечения входа/выхода расчетной области [64]

в первом приближении принимаемые плоскими сечениями, свободными от касательных нагрузок.

Каждый l -й участок стенки тракта обладает собственной поврежденностью D_yx m) ^G [0; 1] по выполнению m -й функции. Функциональность участка стенки тракта связана с поврежденностью формулой F _(Z)(m) = 1 - D_{yx m)}, функциональность, отличная от 1, является количественной мерой снижения функций тракта. В рамках данной статьи рассматриваются функциональные нарушения по секреторной ( m = 1) и моторной функциям ( m = 2) тракта.

Предполагается, что при нарушении секреторной функции F снижается интенсивность массового источника соляной кислоты в области ∂Ω . С медицинской точки зрения гипосекреция может соответствовать заболеванию атрофическим гастритом различной степени тяжести [38] . Например, при F = 0,5 интенсивность массового источника снижена в два раза, что соответствует средней тяжести заболевания. В случае тяжелых форм заболевания скорость секреции кислоты может снижаться до нескольких процентов от нормального физиологического уровня [29] . В рамках работы не рассматривается гиперсекреция кислоты, которая, скорее, является следствием нарушений в регуляции, в то время как пониженная секреция может быть вызвана повреждением секреторных клеток. Аналогично в модели рассматривается только снижение интенсивности массового источника гидрокарбоната натрия, т.е. нарушения F _(/)(1) ( l = 3,5 ) антрума, дуоденума, поджелудочной железы и печени. Снижение уровня секреции щелочи в дуоденуме может быть связано с рядом заболеваний. Например, у пациентов с язвой дуоденума скорость секреции гидрокарбоната натрия в двенадцатиперстной кишке почти в два–три раза ниже, чем у здоровых людей [32] . Возможно, именно снижение функции секреции приводит к истончению слизистого слоя тракта и образованию язвы. Секреция гидрокарбоната натрия с соком поджелудочной железы также может уменьшаться вследствие заболеваний [19] , возраста [65] или под действием негативных факторов, например, курения [36] .

Нарушения моторной функции выражаются в снижении амплитуды перистальтических волн в антруме и дуоденуме, в снижении степени сжатия пилорического сфинктера, что может быть вызвано слабостью мышц циркулярного слоя стенки тракта. Другие нарушения моторики, например, изменение периодичности сокращений, не рассматриваются.

Математическая постановка

Для описания среды в антродуоденуме используем диффузионное приближение для гомогенной смеси. Предположим, что компоненты растворены и взаимодействуют на молекулярном уровне, при этом скорости относительного движения учитываются только для определения концентраций компонент, а динамическими и инерционными эффектами за счет относительного движения можно пренебречь. Относительные движения компонент определяются диффузионными механизмами. Кроме того, в уравнения сохранения массы необходимо включить массовые источники за счет процессов секреции, реакции между компонентами. Таким образом, уравнения сохранения массы для компонент смеси могут быть записаны в виде

-( р Y _o) + V - ( p v Y ii ) ) = - V - J _{( z )} + F _{( i )} + S _{( z )} , r eQ , t e [0; T ), i = 0, I , (1)

где r – радиус-вектор пространственных точек, м; ρ – плотность среды, кг/м3; Ω = Ω ∪ ∂Ω – замкнутая область (внутренность всей области Ω и ее граница ∂Ω ); dQ^ - l-я граница области, l = 1, L; Цо - внутренность области, прилегающая к l-й границе, l = 1, L; v - скорость частиц среды, м/с; У^ - массовая доля i-й компоненты, X У = 1, i = 0, I; J(z) - вектор интенсивности потока массы i-й компоненты за счет i диффузионных процессов, кг/(м2^с), i = 0,1; R^ - интенсивность источника массы i-й компоненты за счет реакций между компонентами, кг/(м3-с), i = 0,1; S(/)  - интенсивность массовых источников i-й компоненты первой фазы в области за счет секреции, кг/(м3^с), i = 0,1.

Содержимое антродуоденума является гомогенной смесью – каждая компонента занимает весь ее объем, поэтому при описании компонент оперируем с массовой долей компоненты Y :

X У , ) = 1, i = 0 1 .                                 (2)

i

Уравнение сохранения импульса для вязкой многокомпонентной жидкости имеет вид

∂

— ( p v ) + V - ( p vv ) = - V p + V - T + p g , r gQ , t g [0; T ),               (3)

∂t где p – давление, Па; τ – девиаторная часть тензора напряжений Коши, Па, которую для вязкой несжимаемой жидкости можно записать в виде

T = n ( V v + ( V v ) ^T ), r gQ ,                             (4)

где η – сдвиговая вязкость, Па∙с.

Для ламинарного течения вектор интенсивности потока массы i -й компоненты за счет диффузионных процессов может быть представлен в виде

J(i) =-p K(i)V Y( i), где K – коэффициент диффузии i-й компоненты в полости желудочно-кишечного тракта, м2/с, i = 0,1. В первом приближении K(z) предполагается одинаковым для всех компонент.

Слагаемое источника массы за счет реакции нейтрализации пропорционально произведению концентраций соляной кислоты и гидрокарбоната натрия:

R(i) = k(0)(2)M(i)C(0)C(2), i = 0,3 , где k – константа скорости реакции, м3/(с∙кмоль); M – молярная масса i-й компоненты первой фазы, кг/кмоль, i = 0,1; C^ - молярная концентрация i-й компоненты первой фазы в полости антродуоденума, кмоль/м3, i = 0,1.

Соляная кислота ( i = 0) и гидрокарбонат натрия ( i = 2) расходуются (массовые стоки) в результате реакции (6), при этом образуются (массовые источники) вода

( i = 3), смесь углекислого газа и хлорида натрия ( i = 1), поэтому слагаемое R для реагентов принимается отрицательным, а для продуктов реакции – положительным.

Молярную концентрацию i-й компоненты можно вычислить, используя соотношение

C ( о = Y ₀P / M ( 0 .

Массовые источники компонент за счет секреции зависят от участка тракта, поэтому при дальнейшем описании используем дополнительный индекс области l для источника S . В областях, примыкающих к границам, массовый источник за счет секреции компонент задается в виде

S(;)(l)    F(l)(1)S(i)(l)’ r еЦl) , l 2,5, где S – интенсивность массовых источников i-й компоненты первой фазы в l-й подобласти Ц}, кг/(м3^с); S(NXZ) - интенсивность массовых источников i-й компоненты первой фазы в l-й подобласти Ц7) при отсутствии функциональных нарушений, кг/(м3∙с).

Таким образом, секреторный поток пропорционален функциональности, при F = 0 секреция полностью отсутствует, при F = 1 интенсивность источника соответствует секреции без функциональных нарушений.

Так как в рассматриваемой постановке питательные вещества в антродуоденуме отсутствуют, то интенсивность массовых источников кислоты определяется соотношением

Я N = V⁰   7 = 345

°(0)(2)    3(0)(2) ,1 J, ^,   , где s^°0)(2) - базовый уровень секреции кислоты в области Ц2) (при отсутствии растворенных компонент пищи), кг/(м3∙с).

Скорость секреции гидрокарбоната натрия определяется соотношением еN       о                s(2)(l)[р(1)а(1)Y0)](2)     7 = 2 4 5

S(2)(l)   S(2)(l) + F(l)(ne)   ,        r         у        , l 3, 4, 5 , s (2)(l) + [р(1)а(1)Y(0)J(2)

где s _(2)(Z) - базовый уровень секреции гидрокарбоната натрия (при отсутствии кислоты) в области Ц₇), кг/(м³^с); Fyxne) — функциональность нервной системы по передаче сигнала в область Ц,_}, F _(Z)(пе) е [0; 1]; s_(2)(Z) - константа скорости секреции гидрокарбоната натрия в области Ц_7}, кг/(м³^с); s '_(2XZ) - вторая константа скорости секреции гидрокарбоната натрия в области Ц_}, кг/м³; [р₍₁₎а₍₁ ^ о)](2) - средняя массовая концентрация соляной кислоты вблизи стенки тракта Ц₂₎, кг/м³.

Соотношение вида (10) является аналогом уравнения Михаэлиса–Ментен и применяется для описания воздействий с насыщением. Соотношение (10) отражает известные экспериментальные факты [13], при этом при усилении секреции кислоты в области Ц2) происходит повышение интенсивности секреции гидрокарбоната в областях Ц3р Ц4р Ц5) для нейтрализации кислоты. В (10) присутствует сомножитель F , описывающий влияние функциональности нервной системы на передачу управляющего сигнала, так как в этом случае секреция щелочи и измерение рецепторами кислотности среды осуществляются в разных областях антродуоденума.

Скорость секреции воды в верхней части желудка Ц₂₎ пропорциональна скорости секреции кислоты S_{(3X 2)} = s_(3X2)S _(0X2) • Скорость секреции воды в областях Ц_3}, Ц₄), Ц₅₎ пропорциональна скоростям секреции гидрокарбонатов S_(2)<п . Таким образом, в первом приближении предполагается постоянство концентраций кислоты и щелочи в секретах желез.

На стенках антродуоденума с учетом перистальтического движения в предположении прилипания частиц среды задаются кинематические граничные условия и условия нулевого потока компонент через границу:

8 Y.                           —

v ( t , r ) = d r ( t )/d t ,   —= = 0,   i = 0, I , t g [0; T ),   r ( t ) g5Q_zp   l = 2, 5,      (11)

dn где r(t) g ЭЦ^ - радиус-вектор материальной точки стенки антродуоденальной области желудочно-кишечного тракта. Амплитуда сокращений пропорциональна функциональности области F . На остальных границах исследуемой области (сечения входа/выхода) задаются значения массовых долей компонент первой фазы, давление и условия равенства нулю касательных компонент вектора напряжений:

Y _o = Y /Т , n ’ ^а ‘ ⁿ = Р, t - ( n ' ^CT ' n)n = 0 , t = n ' ^c , t g [0; T ), r gS^_p l = 1,6.   (12)

Система уравнений дополняется начальными условиями в виде

Y _o( t , r ) = Y^ 0), v ( t , r ) = v ⁰ , r gT , t = 0.                         (13)

Определение уровня P H смеси

В медицинских исследованиях для оценки функции желудка применяется щелочной тест – пациенту через рот вводят значительную концентрацию гидрокарбоната натрия и наблюдают за изменением уровня pH [5] . В этом случае уровень pH рассчитывают по приближенным формулам через значение концентрации вещества, находящегося в избытке, при этом концентрация образовавшейся углекислоты не учитывается, так как она (при быстром введении значительных концентраций гидрокарбоната) распадается на воду и углекислый газ (диссоциацией которых пренебрегаем, вероятно, при таких концентрациях углекислый газ выводится из раствора). Формулы для приближенного расчета pH при избытке соляной кислоты и гидрокарбоната натрия соответственно записываются в виде

C o )+x C 2» + ⁴ K^

pH = - 1g ⁽⁰⁾     ^⁰⁾ ------⁽wL,                             (14)

к(2) .(К(2) (1)  (^(2) ^(2) + 1 \w)) pH = 1g0 к(2)+с         , K (1) + C (2) (15) где K(d) - первая константа диссоциации угольной кислоты, моль/л; K(21)) - вторая константа диссоциации угольной кислоты, моль/л; К^ - ионное произведение воды, моль2/л2.

В реальных условиях компоненты могут иметь малые концентрации, поэтому при расчете уровня pH для задачи течения в антродуодемуме целесообразно использовать более точные формулы с учетом концентрации угольной кислоты.

При выводе расчетных формул используются следующие основные положения.

• 1.    В дальнейших выкладках предполагается равенство активности ионов концентрациям, поэтому уровень pH вычисляется через логарифм концентрации ионов оксония:

• 2.    Предполагается независимость констант диссоциации угольной кислоты и воды от параметров среды, в основном в силу гипотезы об изотермичности рассматриваемых процессов. Таким образом, уровень pH будет определяться только концентрацией компонент в антродуоденуме.

• 3.    Вместо первой константы диссоциации угольной кислоты используется значение кажущейся константы, учитывающей равновесие угольной кислоты с гидратом диоксида углерода.

• 4.    Вторая ступень ионизации угольной кислоты в водном растворе не рассматривается, так как ее учет не влияет на точность оценки pH при любых концентрациях.

• 5.    Поскольку время реакции между кислотой и гидрокарбонатом натрия намного меньше рассматриваемых временных масштабов, полагается, что в любой точке среды присутствует только одна из этих компонент, находящихся в избытке. В этой связи вывод формулы pH проведен для двух случаев, в первом случае для водного раствора гидрокарбоната натрия и угольной кислоты, во втором – для водного раствора соляной и угольной кислот.

pH = - -aHO ' )] = - 1д[Н з О ⁺ ] ,

где a(H₃O ⁺ ) - активность ионов оксония; [H₃O ⁺ ] - концентрация ионов оксония.

Для вывода расчетной формулы pH смеси гидрокарбоната натрия с концентрацией C и угольной кислоты с концентрацией C рассматриваются уравнения реакций, описывающие ионизацию аниона HCO ^- (который образовался вследствие диссоциации гидрокарбоната натрия), угольной кислоты по первой ступени и автопротолиз воды:

HCO ^- + H₂O <---> H₂CO₃ + OH - ,

HCO ^- + Ho <—> h₃o ⁺ + co 2 , ^{3      2             3           3}                                       (17)

H₂CO₃ + H₂O <---> H₃O ⁺ + HCO ^- ,

H₂O + H₂O <--- > H₃O ⁺ + OH - .

Уравнения материального баланса для системы (17) имеют вид

c₍₂ ) = [HCO -1+ [H₂CO₃1 + [CO 2^- ],

C(1 )= [H2CO3]2 + [HCO- ]2, где [HCO31, [H2CO31 - концентрации ионов в первых двух реакциях (17); [H2CO3]2 , [HCO- ]2 - концентрации ионов в третьей реакции (17).

В силу того что концентрация частиц, отдавших протоны, равна концентрации частиц, присоединивших протоны, уравнение электронейтральности записывается в виде

[H2CO3 ] + [H3O+ ] = [OH- ] + [CO32- ] + [HCO- ]2.(19)

Уравнения дополняются соотношениями для констант диссоциации кислоты и ионного произведения воды:

K(d) = K(2 )(H2CO3) = [H3O+ ][HCO- ]/[H2CO3],(20)

K(2') = K(2)(HCO-) = [H3O+ ||CO2]/[HCO-],(21)

K(w) = [H3O+ ][OH-].(22)

Используя второе уравнение (18), получаем:

[H2CO3] = [H2CO3]! + [H2CO3]2 = [H2CO3]! + C(2) -[HCO-]2.(23)

Выразим разность [H₂CO₃], - [HCO ^- ]₂ из (23) и подставим в (19):

[H2CO3 ] - C(1) + [H3O+ ] = [OH- ] + [CO2- ].(24)

Из выражений для констант диссоциации угольной кислоты (20)–(21) и уравнений материального баланса (18) можно получить соотношения для [H 2 CO 3 ], [CO 2 ^- ]:

[H₂CO₃] =---------- ⁽ ! ⁾. ■   ⁽²⁾₊ ----------[H₃O ⁺ ] ² ,

• ^{2   3}    [H₃O ⁺ ] ² + K ^{( 2} ) [H₃O ⁺ ] + KK ³

  [CO 2 ^- ] =

  
  

' (1) ⁺ ^(2)

ГН О⁺ 1² + AC^{( 2} )ГН 0+1 + Id) ^{2 )}K^{( 2} ) ^{(1) (2) [11}3^ ^{] +1 v}(1) ^[113^ ^{] + 1} ^(1) ^^(2)

Подставляя (25),  (26), а также [OH ] из (22) в формулу (24), после преобразований можно получить уравнение четвертой степени относительно [H3O+ ]:

ru о⁺ "1⁴ \ (C _|_ к ⁽²ЛГЫ П⁺ Л^гд-(К²² )^⁽²) C IC)² )    К       O⁺1² i

^[H3^{O ] + ( C} (2) ⁺ K (!) ^)[H3^{O ] + (} K (!) K (2) ^- C (!) K (!) ^- K ( w )^)[H3^{O ] +}

⁽h^⁽ )         c)) ic⁽)         JC) H⁺l— IC) ) 1C⁽ )

^{+ (} C (2) K (!) K (2)   ² C (!) K (!) K (2)    K ( w ) K (!) ^)[H3^{O ]}   K ( w ) K (!) K (2)   ⁰¹

В растворе кислот ионизация угольной кислоты протекает по первой ступени, осуществляется автопротолиз воды, а соляная кислота с концентрацией C практически полностью подвергается ионизации:

HCl + H₂O <---> H₃O ⁺ + Cl ^- .

Уравнение электронейтральности раствора кислот с    учетом

C (0) = C (HCl) = [Cl ^- ]:

|HO ' ] = [OH ^- ] + [HCO ^- ] + C (₀) .

Используя соотношения для первой константы диссоциации и ионного произведения воды, после преобразований можно получить кубическое уравнение относительно [H₃O ⁺ ]:

⁺ T³      JK^{( 2} )                    ⁺ "I²            J^^{( 2} )         TC)- )                  ГЛ+l    C) )

^[H3^{O ]} + ⁽ K (!)    C (0) ) ^[H3^{O ]   (} C (0) K (!) + C (!) K (!) + K ( w )^)[H3^{O ]} K (!) K ( w )    0 .   ⁽³⁰⁾

Для решения уравнений (27) и (30) в численной реализации модели использован метод касательных. Вычисление десятичного логарифма с обратным знаком от концентрации ионов оксония в соответствии с формулой (16) приводит к итоговому значению pH раствора. Следует заметить, что присутствие в растворе соли NaCl не оказывает влияния на уровень pH.

Идентификация параметров

Основные трудности идентификации вызывает определение пространственно распределенных реологических характеристик содержимого желудка на различных стадиях пищеварения. На данном этапе параметры секреции компонентов определены на основе данных литературы по максимальной и базовой скоростям секреции [13] (табл. 1). Реакция ионного обмена протекает практически мгновенно: k > 10⁴ м³/(кмоль∙с), в расчетах использовано минимальное значение [5] . Коэффициенты диффузии K для компонент первой фазы приняты равными М0 9 м 2 /с [5] . Константы диссоциации принимаются равными K^ d ) = 4,9•10^-7 моль/л, K(^ ) = 5,62•10^-11 моль/л, значение ионного произведения воды равно K = 5,62∙10^–11 моль²/л² (при температуре 35 °С) [9] .

Базовые параметры моторики (при отсутствии функциональных нарушений) заданы на основе известных литературных данных [52] и результатов ультразвукового исследования [11] : периодичность – 18 с, ширина волны – 0,02 м, амплитуда – 0,009 м. Волна инициируется в теле желудка и распространяется к пилорическому отверстию со скоростью 0,0022 м/с в течение 38 с. Параметры волн в двенадцатиперстной кишке: периодичность – 9 с, ширина волны – 0,04 м, амплитуда – 0,0035 м, волна инициируется вблизи пилорического отверстия и распространяется со скоростью 0,005 м/с в течение 36 с. Открытие и закрытие пилорического отверстия осуществляется в течение 2 с каждые 18 с. Таким образом, при заданных параметрах моторика антрального отдела, пилорического отверстия и двенадцатиперстной кишки синхронизирована. Геометрия расчетной области меняется периодически.

Результаты и обсуждение

Алгоритм реконструкции трехмерной формы антродуоденума по результатам ультразвуковых исследований, а также алгоритм перепостроения расчетной сетки для описания перистальтических волн подробно изложены в предыдущих публикациях авторов [11, 4]. Представленные в данной статье результаты получены на примере среднестатистической по геометрическим характеристикам (размерам, форме) антродуоденальной области желудочно-кишечного тракта .

Исследуется влияние изначально повышенной кислотности (например, за счет принятой кислой жидкости) на динамическое распределение кислотности в тракте в зависимости от объема и pH жидкости, наличия функциональных нарушений секреции щелочи, моторики антрума (табл. 2).

В первом сценарии рассматривается случай употребления напитка с нейтральной кислотностью (pH = 7) объемом 170 мл, например, воды. Во втором и третьем сценарии рассматривается случай употребления напитка с повышенной кислотностью (pH = 2,3) объемом 100 и 170 мл соответственно. Такой уровень кислотности наблюдается у лимонного сока, «Кока-колы» и подобных газированных напитков [54] . В четвертом сценарии анализируется распределение кислотности

Таблица 1

Обозначение параметра	Значение параметра
5 0 3 (0)(2)	~0,404∙10–7/ V   кг/(м3∙с)
5 0 3 (2)(3)	~1,75∙10–8/ V   кг/(м3∙с)
3 (2)(3)	~7∙10–8/ V   кг/(м3∙с)
3 (2)(3)	~0,5 кг/м3
5 0 3 (2)(4)	~0,278∙10–8/ V   кг/(м3∙с)
3 (2)(4)	~1,112∙10–8/ V   кг/(м3∙с)
3 (2)(4)	~0,5 кг/м3
5 0 3 (2)(5)	~1,972∙10–7/ V   кг/(м3∙с)
3 (2)(5)	~7,888∙10–7/ V   кг/(м3∙с)
3 (2)(5)	~0,5 кг/м3
3 (3)(2)	~171,3
3 (3)(3)	~395,5
3 (3)(4)	~395,5
3 (3)(5)	~78,3

Таблица 2

№ п/п	Фунциональные нарушения секреции щелочи, F( l )(1) , l = 3,5	Фунциональные нарушения моторики антрума, F (3)(3)	Объем напитка, мл	Кислотность напитка, pH
1	1	1	170	7
2	1	1	100	2,3
3	1	1	170	2,3
4	1	1	170	3,5
5	0,4	1	170	2,3
6	1	0,75	170	2,3

Таблица параметров секреции, оценка по [13]

Параметры для сценариев модели

в желудочно-кишечном тракте при употреблении напитка с уровнем pH = 3,5 объемом 170 мл, что соответствует, например, яблочному, апельсиновому соку или другим фруктовым сокам и некоторым газированным напиткам. В сценариях 1–4 какие-либо функциональные нарушения в антродуоденуме отсутствуют, в частности, интенсивность секреции соляной кислоты и гидрокарбоната натрия соответствует физиологическим уровням у здорового человека. В сценарии 5 рассматривается случай употребления напитка (pH = 2,3, объем 170 мл) при наличии функциональных нарушений секреции гидрокарбоната натрия (F(j№ = 0,4, l = 3, 5). В сценарии 6 анализируется влияние нарушений моторики антрума ( F = 0,75) на характеристики течения жидкости в антродуоденуме при употреблении кислого напитка (pH = 2,3, объем 170 мл).

На рис. 2 отмечены четыре точки мониторинга в пристеночном слое тела желудка (точка 1), пилорического отдела (точка 2), луковицы двенадцатиперстной кишки (точка 3), в начальном сегменте нисходящей части дуоденума (точка 4).

Анализируя результаты, мы можем видеть, что во всех сценариях в полости тела желудка кислотность смеси составляет от 2 до 3,5 pH (рис. 2). Полученные результаты соответствуют физиологическим нормативам. В сценариях 1, 4 в пристеночных слоях полости антрума и двенадцатиперстной кишки образуется область меньшей кислотности (от 5 до 7 pH) для защиты от негативного воздействия (рис. 2, a , г ).

В сценариях 2, 3, 5, 6 можно наблюдать области повышенной кислотности (менее 4 pH) в полости пилорического отдела желудка и дуоденума (рис. 2, б , в , д , е ), что может оказывать негативное воздействие на состояние слизистой оболочки тракта. Следует отметить, что зоны с низким pH имеют различную локализацию: в сценариях 2, 3 аномально низкие pH наблюдаются в области луковицы двенадцатиперстной кишки, в сценарии 5 высокая кислотность образуется во всей верхней части дуоденума и в начальном сегменте нисходящей части двенадцатиперстной кишки, а в сценарии 6 можно видеть только небольшой участок повышенной кислотности в области луковицы двенадцатиперстной кишки.

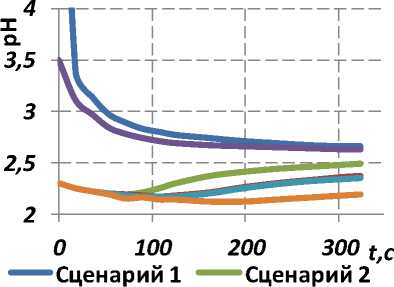
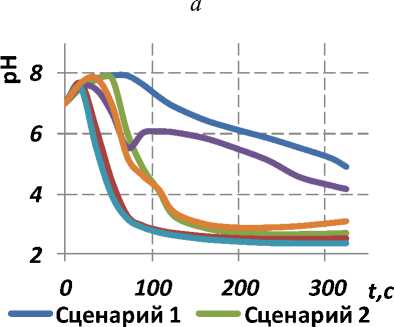
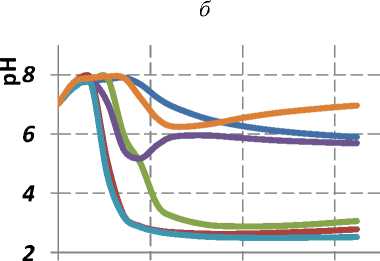
В первом сценарии можно наблюдать, что кислотность в приграничных слоях желудка находится в пределах физиологической нормы (рис. 3, а ). В пилорическом отделе желудка и луковице двенадцатиперстной кишки наблюдается небольшое повышение кислотности вследствие поступления кислотного содержимого желудка в дуоденум.

Во втором и третьем сценарии можно наблюдать значительно повышенную кислотность в пилорическом отделе желудка, луковице двенадцатиперстной кишки и в нисходящей части двенадцатиперстной кишки вследствие наличия кислого напитка (рис. 3, б , в , г ). Постепенно (после 3 минут от приема напитка) уровень pH в пристеночном слое пилорического отдела желудка начинает медленно возрастать вследствие нейтрализации кислоты и перехода кислого напитка в кишечник (см. рис. 3, б ). В силу поступления напитка в кишечник в области луковицы дуоденума кислотность остается очень высокой (2,3 pH) (см. рис. 3, в ). В области нисходящей части двенадцатиперстной кишки уровень pH начинает медленно возрастать (спустя 3 минуты после приема напитка) вследствие нейтрализации кислоты гидрокарбонатом натрия за счет массового источника в области l = 5 (выход протоков от поджелудочной железы и печени) (см. рис. 3, г ). Напиток большего объема (сценарий 2) быстрее поступает в кишечник, формируя низкие уровни pH = 2,94 уже в первые 90 с после начала моделируемой стадии пищеварения (см. рис. 3, в ).

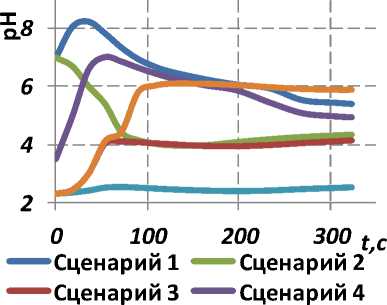
В четвертом сценарии уровень pH в пристеночном слое тела желудка и пилорического отдела близок к значениям, полученным в первом сценарии при употреблении воды (см. рис. 3, а , б ). В этом случае механизмы защиты слизистой антрума и пилорического отдела справляются с нейтрализацией агрессивного воздействия кислоты. Вследствие поступления кислого содержимого в кишечник pH в дуоденуме понижается до 4 в течение 5,5 минут после приема напитка, оставаясь

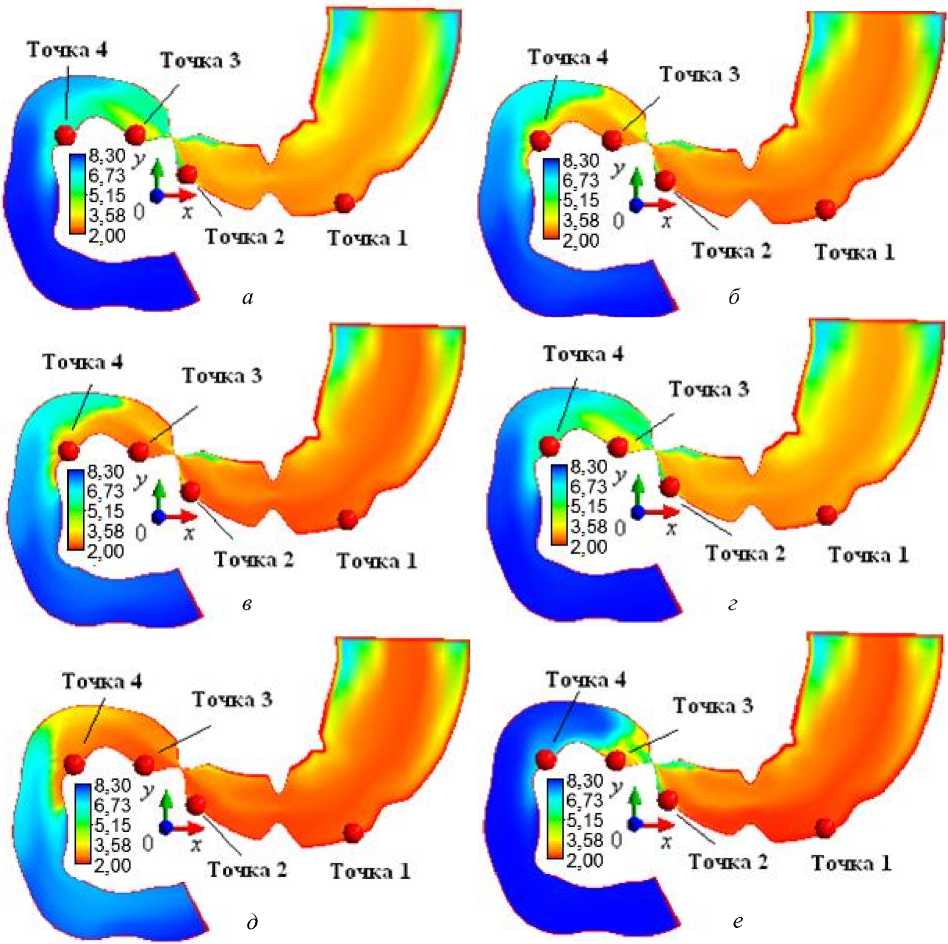
Рис. 2. Уровень pH, t = 330 c: а – сценарий 1; б – сценарий 2; в – сценарий 3; г – сценарий 4; д – сценарий 5; е – сценарий 6

значительно выше значений pH, полученных в сценарии 3 (см. рис. 3, в ). В области нисходящей части двенадцатиперстной кишки pH восстанавливается до 5,7 вследствие нейтрализации кислоты (см. рис. 3, г ), что очень близко к значениям, полученным в сценарии 1 (pH = 5,9).

При нарушении функции секреции гидрокарбоната натрия (сценарий 5) пилорический отдел желудка не может нейтрализовать аномально избыточную кислотность (pH = 2,5) на протяжении всего времени моделирования (см. рис. 3, б ). В этом случае следует ожидать бóльшую вероятность локализации повреждений слизистого покрова в желудке по сравнению с другими сценариями. Кроме того, если в сценариях 2 и 3 зона низких значений pH в верхней части двенадцатиперстной кишки формируется преимущественно вблизи вогнутой стенки дуоденума, то в сценарии 5 высокая кислотность смеси обнаруживается вблизи вогнутой и выпуклой стенок двенадцатиперстной кишки.

^^^^»Сценарий 3 ^^^^^ Сценарий 4

i Сценарий 5 ^^^^» Сценарий 6

^^^^»Сценарий 5 ^^^^w Сценарий 6

с   Сценарий 3 с Сценарий 4

с   Сценарий 5 ^^^ ■ l Сценарий 6

0     100    200    300 t,c

^^^^еСценарий 1 ^^^^е Сценарий 2 с Сценарий 3 ^^^^еСценарий 4

^^^^Сценарий 5 ^^^™Сценарий 6

в

г

Рис. 3. Динамика уровня pH вблизи стенки тракта в различных частях желудочно-кишечного тракта: а – тело желудка (точка 1); б – пилорический отдел (точка 2); в – луковица двенадцатиперстной кишки (точка 3); г – нисходящая часть двенадцатиперстной кишки (точка 4)

В сценарии 6 вследствие наличия нарушений моторной функции антрума переход кислого содержимого желудка в кишечник осуществляется медленней, чем в сценариях 1–5. Например, при открытии пилорического отверстия скорость течения в наименьшем сечении сфинктера составляет 0,01 м/с в сценарии 5 и 0,019 м/с в сценарии 1. В этой связи в сценарии 6 кишечник успешно нейтрализует кислоту, поэтому аномально низкие pH наблюдаются только в точке мониторинга № 3 (в небольшом участке луковицы двенадцатиперстной кишки).

В целом можно отметить, что при отсутствии функциональных нарушений гидрокарбонат натрия значительно эффективней нейтрализует избыточную кислотность в антродуоденуме при употреблении заданного объема напитка с pH > 3,5. Напитки с pH = 2,3 обладают существенно большим повреждающим потенциалом для слизистой оболочки стенки желудочно-кишечного тракта, так как в сценарии 3 в течение всего расчетного времени уровень кислотности в антродуоденуме остается критически высоким. При наличии нарушений секреции щелочи ситуация дополнительно усугубляется расширением площади потенциального поражения стенки тракта. Негативное воздействие кислоты может выражаться в подавлении способностей к восстановлению клеток слизистого слоя [37] .

Полученные результаты по распределению кислотности в тракте согласуются с известными данными экспериментов: у здоровых людей средний уровень pH в теле желудка равен 2,7 [30] , а при употреблении «Кока-колы» достоверно увеличивается время повышенной кислотности в дуоденуме [51] .

Заключение

Разработанная математическая модель для описания процесса течения в антродуоденуме позволяет оценивать и прогнозировать уровень кислотности в полости тракта. Уровень pH в антродуоденуме может изменяться в зависимости от индивидуальных параметров формы и моторики тракта, наличия секреторных функциональных нарушений, объема и состава принятой пищи. В связи с этим предложенные в статье подходы в дальнейшем могут быть использованы для предоставления индивидуальных рекомендаций по потреблению напитков и пищи с повышенной кислотностью.

Используя разработанную модель, можно выделить области аномально повышенной кислотности в антральном отделе желудке и в дуоденуме. Однако для предоставления прогнозных количественных оценок развития нарушений требуется более детальное рассмотрение механизмов повреждения и восстановления стенки тракта, в том числе при воздействиях соляной кислоты, химических веществ, содержащихся в пище, лекарственных препаратов. Вполне возможно, что однократное химическое воздействие не приведет к развитию патологий. Например, в экспериментальных исследованиях показана возможность быстрой регенерации клеток слизистой стенки желудка [33, 62] и дуоденума [22, 47] . В этой связи требуется учитывать периодичность принятия пищи для рассмотрения циклов повреждения– восстановления.

Для более адекватного представления процесса течения пищи необходимо развивать модели многофазного течения с учетом упругих свойств стенок канала, регуляторных взаимодействий с другими органами и системами, в частности, с двенадцатиперстной кишкой и билиарной системой [6, 42, 43]. Актуальной проблемой остается исследование влияния реологических свойств биожидкости на характеристики процесса течения.

Благодарность

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-01-00126_a.