Течение нелинейной упруговязкой жидкости в плоском канале под действием заданного градиента давления

кинематически допустимыми, то есть удовлетворять как гидродинамическим уравнениям, так и законам термодинамики и условиям на границах, и лежать в пределах рассматриваемой геометрической зоны.

При исследовании работоспособности различных реологических моделей часто ограничиваются куэттовским течением, в котором кинематика потока известна заранее, а эффективная вязкость, а также первая и вторая разности нормальных напряжений подлежат определению. Многие линейные и нелинейные модели описывают такие течения вполне реалистично. Другой тип течения, используемый для тестирования реологических моделей, — течение Пуазейля, в котором скорости определяются путем решения краевой задачи. Для этого типа течений получение точных решений уравнений движения является задачей более сложной, но и более информативной. Исследования, выполненные Трусделлом и Ноллом [1], Колеманом [2], Данном и Фосдиком [3] показали, что существуют кинематически допустимые течения, в которых мощность напряжения может становиться отрицательной. Едва ли возможно, что подобные движения могут реализовываться в природе. Изучение течения вокруг тела, проведенное Альтманом и Денном для линейной упруговязкой жидкости Максвелла [4], привело авторов к заключению, что условие El 2 = VRe We = 1 (где Re и We — числа Рейнольдса и Вайсенберга) разграничивает две различных ситуации. В докритическом случае (E1 2 <  1) уравнения, описывающие течение, относятся к эллиптическому типу и имеют гладкие непрерывные решения. В закритическом случае (El₂ >  1) уравнения гиперболичны и их решения имеют сильные тангенциальные разрывы. Анализ некоторых нелинейных реологических моделей показал, что краевая задача о плоскопараллельном течении в канале под действием перепада давления может иметь неединственное решение и приводить к слабым тангенциальным разрывам в профиле скорости. Так исследование течения четырехконстантной жидкости Олдройда в трубе [5] показало возможность неединственности решения задачи и немонотонности распределения градиента скорости в радиальном направлении. В зависимости от значений перепада давления и отношения времени ретардации к времени релаксации вычисленные профили скорости либо имеют гладкую параболическую форму, либо содержат слабые тангенциальные разрывы. Кривые течения такой жидкости проявляют гистерезисный характер. В работах [6, 7] рассмотрены одномерные течения раствора полимера в плоском канале под действием градиента давления, в которых для описания реологических свойств выбраны две модели. Первая является обобщением феноменологической модели Джеффриса [6] и содержит объективную временную производную с шестью произвольными материальными константами. Вторая — дифференциальная векторная модель, предложенная Реммелгасом, Харрисоном и Лилом, является аппроксимацией статистической модели Дои–Эдвардса–Марруччи–Гриззути [7]. Для этих двух моделей получены точные аналитические решения задачи течения в плоском канале. Показано, что в обоих случаях, в зависимости от исходных параметров модели, задача может иметь как единственное, так и неединственное решение. Профили скорости могут быть либо гладкими, почти параболическими, либо содержать слабые тангенциальные разрывы. Найдены критериальные условия появления неоднозначных режимов течения.

Целью данной работы является поиск всех аналитических решений задачи течения в плоском канале под действием постоянного градиента давления нелинейной упруговязкой жидкости, описываемой модифицированной реологической моделью Виноградова–Покровского [8]. Модель была получена из анализа динамики невзаимодействующих гантелей, движущихся в нелинейной анизотропной среде. Гантель состоит из двух бусинок, соединённых пружинкой; форма и ориентация гантели в потоке характеризуется тензором анизотропии a=

Зй»-¹1 ( Р 2 >  0 3

где ρ — вектор, соединяющий концы гантели и описывающий относительное движение бусинок, ( р ² ) ₀ — равновесное значение выражения (р 2 > + (р 2 > + (р 2 ) , I — единичный тензор. В равновесном состоянии a = 0.

В общем случае модели Виноградова–Покровского уравнение движения, выражение для тензора напряжения и эволюционное уравнение для тензора анизотропии a имеют следующий вид [8]:

I dV      V7

= V- о ,

р — + V-Vv

V 51

о = - p I + 3 — a , ^T 0

d a v 1 + ( к-P ) I_x    2 в

+ a+          a = D - 3—a - a dt            t0           3       t0

где v — скорость среды; V — набла-оператор; р — плотность; о , D — тензоры напряжений и скорости деформаций; p — гидростатическое давление; в и к — феноменологические параметры модели, характеризующие вклады, связанные с анизотропией ( в учитывает ориентацию макромолекулярного клубка, к — его размеры); п ₀ и т ₀ — начальные значения сдвиговой вязкости и времени релаксации;

V a — верхняя конвективная производная тензора анизотропии; I1 = aii — первый инвариант тензора анизотропии.

На основе этой модели в условиях простого сдвига и одноосного растяжения были исследованы вискозиметрические функции и продемонстрировано соответствие теоретических зависимостей и экспериментальных данных для растворов и расплавов линейных полимеров различных молекулярных весов и концентраций [9, 10]. Это позволило приступить к расчетам более сложных течений, нежели вискозиметрические, в частности стационарного течения в бесконечной круглой трубе, а также некоторых двухмерных течений. Проверка модели осуществлялась на простом сдвиговом течении с наложенными малыми осциллирующими колебаниями в параллельном и ортогональном сдвигу направлениях. В результате численного эксперимента были получены зависимости тензора напряжений от градиентов скорости и времени, что позволило рассчитать составляющие комплексного модуля сдвига, динамической вязкости и угла динамических потерь в зависимости от частоты вынуждающих колебаний, скорости сдвига и числа Деборы (De). Одномерная задача течения в плоском канале под действием постоянного градиента давления для жидкости, описываемой такой моделью, была решена ранее методом последовательных приближений и итерационным численным методом [9, 10]. Обзор работ данного направления можно найти в [11].

• 2.    Аналитическое решение одномерной задачи

Рассматривается задача определения профиля скорости и компонент тензора анизотропии a для нелинейной вязкоупругой жидкости, движущейся в плоском канале под действием постоянного перепада давления. Высота канала — 2 h , длина — L .

Начало координат располагается в середине высоты канала, ось x направлена вдоль потока, ось y — перпендикулярно стенкам, ось z — перпендикулярно осям x и y .

В случае стационарного плоскопараллельного течения система (1)–(3) имеет вид:

• ₃ n o ^d a xy = d p t ₀ 5 y 5 x ’

• 3 П о ^d a yy = d p

T ^d y 5 y ’

„   5 v_x , 1 + ( к-R ) I

• -2 a.; +

dy d v 1 + (к-p) I

• - u / + —-~ a dУT

xx

-3— ( a² + a 2 ) , xxxy

^T 0

1 d v_x

= ^x

' xy   3 5 y

P

• ³ -a xy ⁽ a xx ⁺ a yy ) , ^T 0

1 + ( K-P ) 1 1          Rz 2    2.

a yy     ^{3     (} a xy ⁺ a yy ) ^.

^T o                  ^T o

Предположим, что распределение давления в канале представимо как L - X

p(x, y) = p1 l + p2(y), причем p2(0) = 0. Для течения в плоском канале при заданном перепаде давления характерными значениями являются: половина высоты канала h , Аpx градиент давления -1,, начальная сдвиговая вязкость п0, начальное время г                                    y        Vxт0    i т05vx 5V релаксации т0. Введем безразмерные переменные Z = ~, V = ^“0, Y = “°—x = —, 0                                              A h 5y    5Z

• т₀ p         А p j т₀ h

P = 0 1 , G = ————. Компоненты тензора анизотропии а являются безразмерными По           L По по определению.

Квадрат компоненты тензора анизотропии a_xy обозначим через K = a ^y . Подставив введенные соотношения в уравнение движения (4) и проинтегрировав его по Z , получим:

• a_xy = G ^ = V K .                                                             (9)

xy 3

В безразмерном виде уравнения (6)–(8) записываются следующим образом:

• ^- 2 ^Y a xy ^{+( 1 + ( K-P )} 1 1 ) a xx    ^{3 p} ( aL ⁺ a² ) ,

  
  

  ^- Y a yy ⁺ ( 1 ^{+ ( K - P ) 1} 1 ) a xy = 3 ^{Y- 3 P} a xy ( a xx ⁺ a yy ) ,

^{( 1 + ( K - P ) 1} 1 ) a yy = ^{- 3 P} ( a^ xy ⁺ a 2 y ) .

Из системы уравнений (10)–(12) выразим компоненты тензора анизотропии и скорость деформации как функции K

a yy

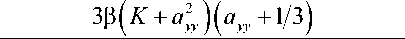
(a„ +13) + 2(к-р)(K + a,, (a,, +13)) ’

2K axx  % + 7   , i M ’

(ay, +1/3)

i

Y =

2 V K 1 + 2 ( к + 2 p ) a y, к

1 + 7—K—\ к (ayy + V3)JJ

(a,, + 13)

.

Компонента a xx тензора анизотропии и скорость сдвига у выражаются через компоненту a_yy , которая определяется нелинейным алгебраическим уравнением (13). Исследуем в первую очередь свойства этого уравнения.

Уравнение (13) является полиномом третьей степени относительно компоненты ayy с коэффициентами, зависящими от параметров модели и безразмерной координаты Z • Следовательно, количество действительных решений и их значения могут меняться как в пространстве координат при фиксированных значениях параметров модели, так и с изменением самих параметров. Перепишем это уравнение в форме полинома a3,, + Aa,, + Ba,, + C = 0, (16)

. 1   1 _D 1         в K

£ = 2 к + p , и проведём исследование его решений.

где A = — + — , В = K +--, C =---,

3 V 3-      ^

Количество корней уравнения (16) определяется знаком дискриминанта

1 L A 3 AB

+ - 2 — —- + C

к 27 3

,

который можно представить полиномом третей степени относительно переменной K :

Q = K ³ + A ( р , к ) K ² + В_х ( р , к ) K + C 1 ( р , к ) ,

где

A =

243 р 2- 162 р- 54 р^+ 30 ^-^ 2- 9 36 ^ 2

В1 =

2^3р - 9^2Р - 27^р - ^3 +12^2 - 9^ + 54р

54 ^ 4

C = 6^ 2 - 9

¹      324 ^ 4

Если Q >0, то уравнение (16) имеет один действительный и два комплексных сопряжённых корня; если Q =0, — три действительных корня, из которых два равны между собой; если Q <0, — три различных действительных корня.

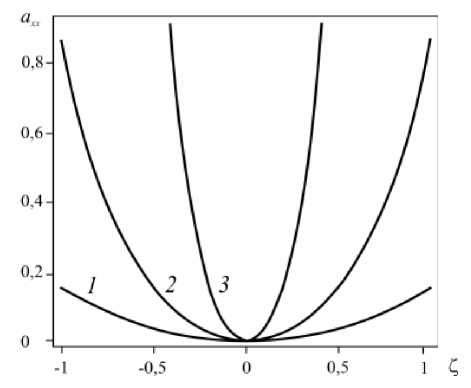
На рисунке 1 приведены результаты решения уравнения Q (K, Р, к) = 0, найденные для нескольких соотношений параметров модели. В точках, принадлежащих кривым Q(K,Р,к), соотношение параметров таково, что уравнение (16) имеет два различных действительных корня. Ниже кривых Q(K, Р, к) детерминант (18) имеет отрицательное

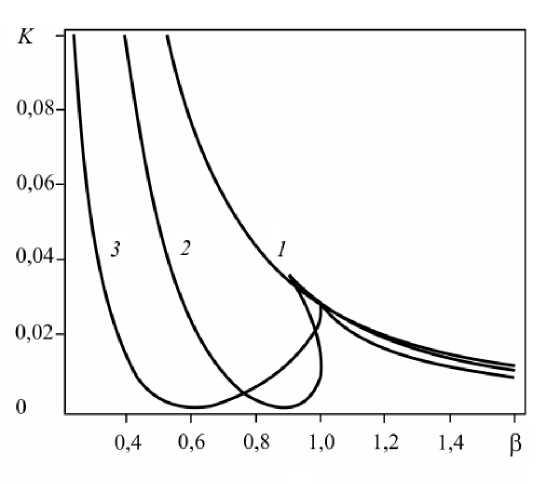
Рис. 1. Графическое представление решений уравнения (16) для соотношений параметров модели: к = р (кривая 1 ), к = 1,2 р ( 2 ), к = 2 в ( 3 )

значение, и в этой области существуют три действительных решения для a_yy . В области выше соответствующей кривой Q ( K , в , к ) значение детерминанта положительно и решение для a_yy единственно.

Распределение компоненты тензора ориентации a yy по высоте плоского канала Z можно представить в виде параметрической зависимости

a =_        Зр( K + ayy")(ayy +1/3)

ayy + 1/3 + 2(к-в)(K + ayy (ayy z =

3 K

G ^,

где роль параметра играет K . Анализ системы (19), (20) показывает, что при K = 0

2 к + в .

компонента a_yy может принимать три значения: a_yy = 0 , a_yy = - 1/3 и a yy

При стремлении к бесконечности перепада давления G и, соответственно K , компонента а имеет предел lim a ^ yy                      K ^го yy

^^^^н

в

2---в . Значение, к которому стремится a yy

при G ^ го, предположительно связано с предельной ориентацией структуры материала. В дальнейшем исследовании будем использовать только соотношение к = 1,20 , которое, как показано в статье [11], позволяет для расплавов полимеров получить результаты, наилучшим образом соответствующие экспериментальным данным.

Поскольку в отсутствие приложенного перепада давления (то есть при K = 0) все компоненты напряжений должны быть равны нулю, следовательно, и компонента ayy должна быть равна нулю. Все решения, имеющие при K = 0 ненулевые значения и расположенные ниже предельного значения ayy =-5/17, являются физически нереализуемыми. Отметим, что для параметра 0 > 1 физически реализуемых решений не существует.

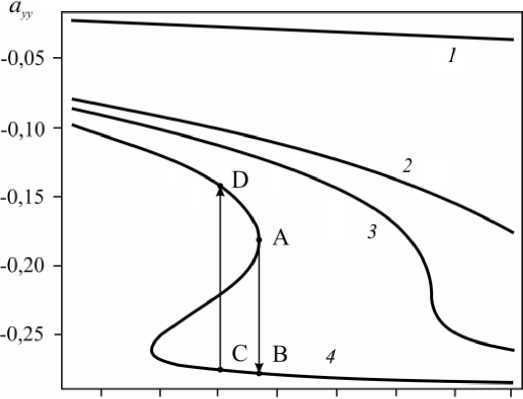
0,026 0,028 0,03 0,032 0,034 0,036 0,038 К

Рис. 2. Зависимость компоненты a yy от параметра K при к = 1,2 р и значениях р , равных: 0,3 (кривая 1 ); 0,6 ( 2 ); 0,8 (3); 0,95 ( 4 )

Физически допустимым решениям соответствуют представленные на рисунке 2 зависимости компоненты a yy от K . При изменении параметра 0 характер этих зависимостей меняется: при 0< 0,9 они имеют вид однозначных монотонных функций, а в диапазоне 0,9 < 0 <  1 становятся неоднозначными. В последнем случае при плавном возрастании параметра K и, соответственно, перепада давления G имеет место докритическая бифуркация — появляется неединственность решения (кривая 4 ). Поскольку ответвляющиеся докритические решения неустойчивы при бесконечно малых амплитудах возмущения, наблюдать в природе непрерывную бифуркацию невозможно. Вместо этого реализуется разрывный процесс, в котором возмущенное решение, уходя из области притяжения основного решения, проскакивает через неустойчивое ответвляющееся решение к устойчивому. При возрастании параметра K и, следовательно, перепада давления G от 0 до некоторого критического значения, соответствующего точке А, происходит скачок a_yy на нижнюю ветвь в точку B. В процессе снижения перепада давления обратный переход из точки С на верхнюю ветвь в точку D происходит при другом, более низком, значении K. Такая ситуация типична для нелинейных реологических моделей. В работах [5–7] показано, что для подобных моделей существует область параметров задачи, в которой среди множества решений есть неустойчивые (мощность напряжения отрицательна) и кинематически нереализуемые (выходящие за геометрическую область решения). В квазистационарном режиме модель Виноградова–Покровского допускает единственный переход с нижней ветви кривой на верхнюю по линии, делящей s-образную кривую на две замкнутые области с равными площадями. Как будет показано ниже, переход по этой линии обеспечивает равенство скоростей при подходе слева и справа к точке разрыва.

Распределение a_yy по высоте канала для трех значений перепада давления представлено на рисунке 3. На этом рисунке, а также на рисунках 4 и 5 фрагменты а соответствуют решениям, полученным при 0 = 0,3 . При этом для кривых 1 задан перепад давления G = 0,5 , для кривых 2 — G = 1,0 и для кривых 3 — G = 2,5 . Фрагменты б рисунков отвечают значению параметра 0 = 0,95 , при этом кривым 1 соответствует G = 0,4 , кривым 2 — G = 0,6 и кривым 3 — G = 1,0 . Как видно на рисунке 3, a ,

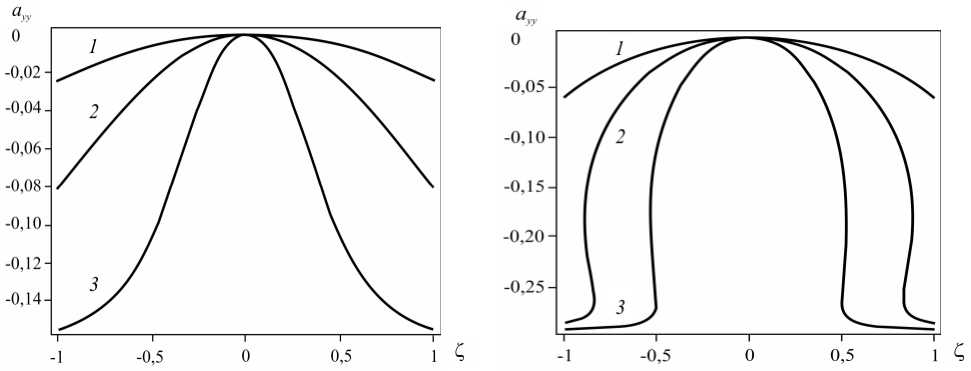
Рис. 3. Зависимость компоненты a_yy тензора анизотропии от поперечной координаты Z при Р = 0,3 ( а ) и Р = 0,95 ( б)

для в = 0,3 и G <  1 распределение a_yy по высоте канала имеет практически параболический вид, однако с увеличением значения параметра в и перепада давления G пространственный интервал, в котором зависимость a_yy ( £ ) имеет параболический вид, постепенно сужается, и вблизи границ a_yy ( £ ) стремится к постоянному значению, равному -5/17. Для в = 0,95 и G >  0,51 распределение a_yy по высоте канала неоднозначно (Рис. 3, б ), что может приводить к сильным разрывам в нормальных напряжениях.

Поскольку компонента a xx тензора анизотропии и скорость сдвига у параметрически зависят от a_yy , то от них следует ожидать аналогичного a_yy поведения. Компонента a_xx определяется уравнением (14). Из уравнения (19) выразим K

K = a„ (ayy +1/3)( 3,4Р a + 1) в( 3,4 a, +1)

и подставим в (14). В результате получим

₍ _ 2 a yy ( 3,4 в a yy + 1 ) '^yy     в ( 3,4 a yy + 1 )

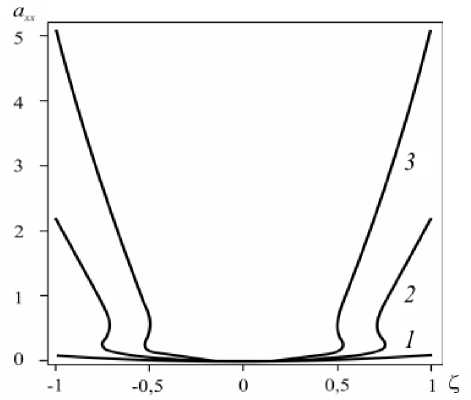
Система уравнений (21) и (22) для фиксированного значения в определяет зависимость a_xx ( K ) через компоненту a_yy , которая в данном случае является параметром. Добавляя к системе (21), (22) выражение (20), построим зависимость a_xx от безразмерной координаты Z для заданного значения безразмерного перепада давления G . Значениям в< 0,9 соответствуют монотонные гладкие профили a xx ( Z ) при любых перепадах давления (Рис. 4, а ). В диапазоне 0,9 < в <  1 при высоких перепадах давления распределение a xx ( Z ) имеет немонотонный характер (Рис. 4, б ).

а                                        б

Рис. 4. Зависимость компоненты a xx от поперечной координаты Z при в = 0,3 ( а ) и в = 0,95 ( б)

Зависимость градиента скорости у от K также можно представить в виде параметрической функции с параметром a yy • Используя условие к = 1,2 в и уравнения (21) и (22), перепишем соотношение для у (15) следующим образом:

I

Y =

a yy ( a yy + ^1/3 )( ^3,4 в a yy + 1 )

в( 3,4 a„ +1)

Г

1 + 6,4 в a yy 1 -кк

(w «„ +1))' в( 3-4 “„ + О))

(a„ +1/3)

По аналогии с зависимостью a_xx ( Z ) может быть построена параметрическая зависимость у ( Z ) •

Определим зависимость скорости V от Z • Для этого вычислим интеграл:

V = Jyd Z + C или

V = Jr dr" da yy + C • da_yy

Из уравнений (20) и (21) найдем производную:

d Z = V3 ( 25 + 1734 a yy в + 10 a„ ( 15 + 17 в ) + 17 a y.. ( 15 + 62 p ) )

dayy

2 G ( 5 + 17 a yy ) 2 в

"„ ( 1 + ³ " „)( ⁵ + ¹⁷ "„ в ) ( 5 + 17 " „ ) в

и подставим ее и выражение (23) для у ( a yy ) в интеграл (25):

„г 3[5+ayy(-15 + 32HI. 25 +1734ayyв ■ 0a.(15 ■ Ч2 ■ Гay,(15+62в)].    „

V J                                (                   \ ₃                             da yy ⁺ C . (2 7)

Для конкретных значений параметров интеграл (27) берется аналитически. Так при в = 0,3 и G = 1 скорость равна:

V =

^^^^^^^s

1620 + 5508 a yy + 98000/ ( 5 + 17 a yy ) 2 - 303450/ ( 5 + 17 a yy ) - 492135 lg ( 5 + 17 a_yy ) +

+

5780 + C .

Неизвестная константа интегрирования С определяется из условия прилипания на границе V ( ± 1) = 0 . Можно показать, что действительное значение V будет существовать только для a yy >  - 17 » - 0,294118 .

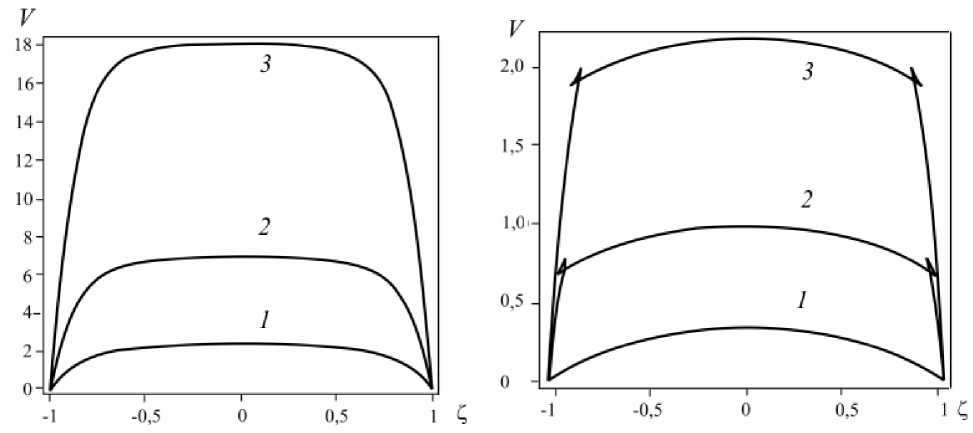
Как видно из рисунка 5, при достаточно высоких перепадах давления профили скорости при значении 0 = 0,3 отличаются от ньютоновских (фрагмент а ), а при 0 = 0,95 имеют замкнутые петли, соответствующие нереализуемым участкам решения системы (19), (20). В точках замыкания петель реализуются слабые тангенциальные разрывы (фрагмент б ).

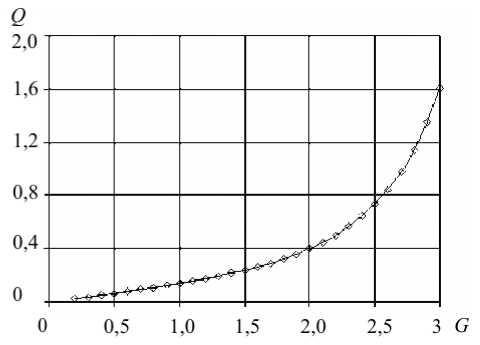
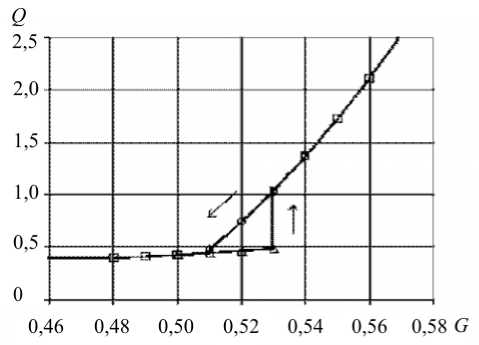
Расходно-напорная кривая, соответствующая параметру 0 = 0,3 (Рис. 6, а ), имеет монотонно возрастающий характер. При значении 0 = 0,95 вид зависимости меняется. В режиме активного нагружения с сохранением квазистационарного характера процесса (то есть при медленном увеличении перепада давления) расход плавно увеличивается до некоторого значения, после чего резко возрастает до нового стационарного состояния и далее продолжает плавно увеличиваться с большей скоростью. В режиме разгрузки (то есть при уменьшении перепада давления) расход плавно снижается до пересечения с кривой активного нагружения, после чего уменьшается с той же скоростью, что и при активном нагружении (Рис. 6, б ).

б

а

Рис. 5. Зависимость скорости V от поперечной координаты Z при 0 = 0,3 ( а ) и 0 = 0,95 ( б)

а                                          б

Рис. 6. Зависимость расхода от перепада давления при в = 0,3 ( а ) и в = 0,95 ( б)

3. Численное решение задачи в двумерной постановке

Рассмотренная выше задача решена далее в двумерной постановке:

д V ^S Vy _п —- + —- = 0, д x д у

Р

(dV dV dV )

__* ₊ V__ - ₊ V__-_v д t x дx ^y ду

д°   д° xy

xx дx    ду ’

( д V

д V

д V,, ^

р —у- + V —y + V —ун я# x у я,.

^д° xy

д t

дx

ду)

дx

+

^д° уу

ду ’

° xx

^^^^^ш

. д к ~ L

■ p + 2 п —- + 3 п 2 а д x       .

д Vx

xx

° уу

ш

д V (

■ p + 2 п —- + 3 п 2 а д у

yy

° xy

v

дx

д V,

9у

д V

• 2    ^в 2

• 3    ( a_xx

^Т 0

ш

3 7( а у

^Т 0

(д Vx  д Vy ) 2 (   д Vy

= п —- + —- + 3п а„—у + а xx

V ду    дx

)

V

дx

yy

xy

xy

xy

д V

д аХх xx

д а

д аХх xx

д t

x

дx

y

^^^^н

2 д V_x

3 д x

1 ^в 2

- 3 ( a_xx

^Т 0

ду

2 a xx

д V

дx

^^^^н

xy

д V_x

ду

д V y

■xy дx

ш

^{д а})у

^{д а}уу

^{д а}уу

д t

x

дx

y

^^^^н

2 д V y

3 д у

Д в 2

- 3   ( axy т0

ду

la xy

д Vy

дx

yy

V x

V x

^д a xx

дx

^{д а}уу

дx

ш

V y

V y

^д a xx

^д у )

^{д а}>у )

ду )

,

,

в

^{3    a}xy ( a xx ^{+ а}уу

^Т 0

х да

- V —^x-УL

) x дx

V y

даху xy

ду

)

,

дV ^1 + (к-р)112 axv   + —--- xy

ду

^Т 0

xx

^^^^н

д V

² а уу— +

1 +(к-Р) 11

ду

^Т 0

yy

d a^    da     5 a^

xy + у   xL + у   xL - a dt      Sx    y dy

dV

xy d x

^^^^™

a xy

e V y

^^^^H

dy

d V y a xx

оx

^^^^H

a yy

dVx +1 +(K-P) Ii

8y

^T 0

a xy

1 ( d Vx 5 Vy ) x+

3 Id y

dx ,

xy xx yy ,

^T 0

где V_x , V — компоненты скорости, n = г--;—⁰—;—

I = a.. + a,,,, . Область решения

1   xxyy

x • y                        ^p , ¹ [1 + ( к-в ) 1 1

представляет собой прямоугольник с размерами H =1 мм и L =50мм , который покрывается сеткой с числом разбиений Nx = 1000 и Ny = 100.

Алгоритм численного решения задачи представляет собой итерационный процесс, на каждом шаге которого сначала методом конечных элементов на треугольной сетке определяются поля скорости и давления при известных с предыдущего шага компонентах тензора анизотропии; затем методом Рунге–Кутты четвёртого порядка решаются эволюционные уравнения для компонент тензора анизотропии с известными из предыдущей итерации компонентами вектора скорости. В алгоритме метода Рунге-Кутты выбран шаг по времени A t = 10 ^{- 3}. В качестве критерия сходимости общего итерационного процесса используется чебышевская норма в ₁ = max | v_k - v_{k h 1} |, где максимум определяется по всем узлам сетки. Аналогичным образом устанавливается критерий сходимости для метода Рунге-Кутты: 8 2 = max | a_k - a_{k h 1} |. Процесс заканчивается при 8 ₁ <10 ^{- 5} и 8 2 <10 ^{- 5}.

На рисунках 7–10 представлены численные (точки) и аналитические (сплошные линии) результаты решения. Фрагменты а рисунков демонстрируют решения, полученные при в = 0,3 ; кривые 1 соответствуют значению G = 1, а кривые 2 — G = 1,5 . Фрагменты б рисунков отвечают значению параметра 0 = 0,95 , при этом кривые 1

соответствует G = 0, 5 , а кривые 2 — G = 0, 55 .

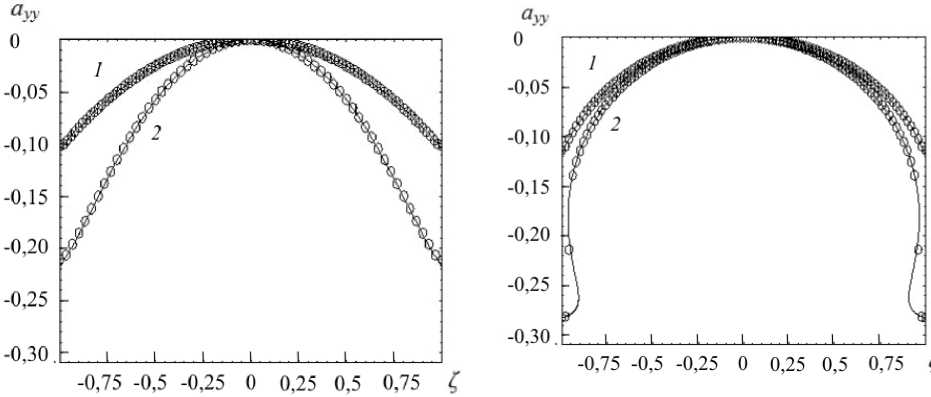
Сравнение численных и аналитических результатов показало, что в докритическом режиме результаты идентичны, а численное решение, отвечающее закритическому режиму, сглаживает скачки в распределении нормальных составляющих тензора анизотропии и дает заниженные значения продольной скорости в режиме активного

б

а

Рис. 7. Профили компоненты тензора анизотропии a_yy при 0 = 0,3 ( а ) и 0 = 0,95 ( б )

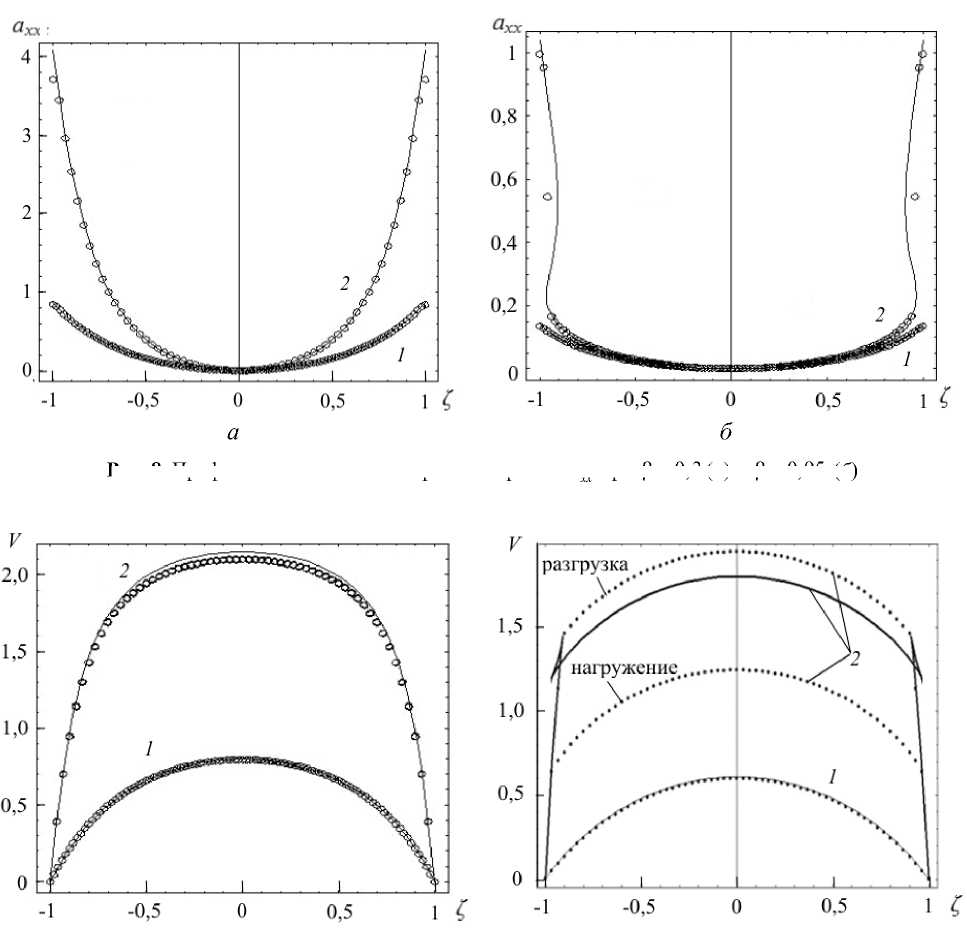
Рис. 8. Профили компоненты тензора анизотропии а при р = 0,3 ( а ) и р = 0,95 ( б)

а

б

Рис. 9. Профили продольной скорости при р = 0,3 ( а ) и р = 0,95 ( б)

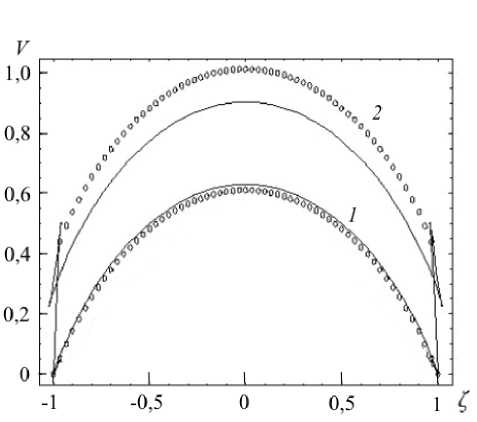
Рис. 10. Профили продольной скорости в области неоднозначности решения ( Р = 0,95) в режиме активного нагружения (кривые 1) и разгрузки ( 2 ) при значении перепада давления G = 0,52

нагружения и завышенные — в режиме разгрузки. В области параметров задачи, для которой появляется неединственность решения (например β = 0,95 , G = 0,52 ), при одном и том же перепаде давления существуют два профиля скорости, отличающихся по форме и величине расхода (Рис. 10, кривые 1 и 2 ). Эта ситуация наблюдается как в аналитическом, так и в численном решении.

• 4.    Выводы

Получены аналитически все действительные решения задачи плоскопараллельного течения нелинейной упруговязкой жидкости в канале под действием заданного перепада давления. Установлено, что в такой постановке задача имеет множество решений, по крайней мере, одно из которых является действительным. Из найденных выделены заведомо физически недопустимые решения.

Определены кинематически допустимые зависимости компонент тензора анизотропии, градиента скорости и продольной скорости от поперечной координаты в параметрическом виде при различных значениях параметров реологической модели.

Установлено, что

– использование реологической модели с параметрами κ =1,2β и 0<β <0,9 приводит при малых градиентах давления к решению, имеющему для компонент тензора анизотропии вид однозначных гладких функций; около оси симметрии зависимость ayy (ζ) имеет параболический характер; при G →∞ компонента ayy стремится β на границе к постоянному значению, равному lim a →-      ; профиль скорости

K→∞ yy 2κ+β гладкий и при малых градиентах давления форма его близка к параболической, а при увеличении градиента давления стремится к П–образной;

– при значениях параметра 0,9 <  β < 1 возможно выделение двух типов решений, соответствующих малым и высоким градиентам давления (гладкие однозначные профили скорости и компонент тензора анизотропии соответствуют малым градиентам; распределение компонент тензора анизотропии и формирование замкнутых петель на профиле скорости связаны с неоднозначностью решения при высоких перепадах давления; кривая звисимости расхода от перепада давления носит гистерезисный характер).

Проведено сравнение численных результатов с аналитическим решением, которое показало, что:

– в докритическом режиме результаты идентичны, а в закритическом режиме численное решение дает более гладкое распределение нормальных составляющих тензора анизотропии и предсказывает заниженные значения продольной скорости в режиме активного нагружения и завышенные — в режиме разгрузки;

• – в области параметров задачи, где появляется неединственность решения , при одном и том же перепаде давления как в аналитическом, так и в численном решениях существуют два профиля скорости, отличающиеся по форме и расходу;

  – сильные разрывы в нормальных компонентах тензора анизотропии, возникающие вследствие неединственности решения при определенной совокупности параметров задачи, не противоречат физическим представлениям о процессах трансформации структуры материала, однако появляющиеся в этом случае разрывы в нормальных напряжениях недопустимы, и при значениях 0,9 <  β < 1 задаваемый перепад давления не должен превышать критического значения.

Работа выполнена при   финансовой   поддержке Российского фонда фундаментальных исследований (проекты   №   09-01-00293,   10-08-96096).