Течение пластического материала между вращающимися плитами: отличительные особенности решения

Ishlinsky Institute for Problems in Mechanics RAS, Moscow, 119526, Russia the flow of rigid perfectly/plastic material between two rotating plates with rough surfaces is considered. An analytic solution to the boundary value problem formulated in this study is obtained by an inverse method under standard assumptions for this class of problems. The main purpose of the present research is to investigate the qualitative behavior of solutions in the vicinity of the line of intersection of two friction surfaces. A comparison between the new solution and other known solutions of boundary value problems, whose formulations also include two intersecting friction surfaces, is made.

Исследование качественного поведения жесткопластических решений вблизи поверхностей трения представляет значительный интерес. В частности, при использовании закона максимального трения идеально жесткопластические решения обычно являются сингулярными вблизи поверхностей трения (некоторые производные от компонент вектора скорости течения материала стремятся к бесконечности при приближении к поверхности) [1, 2]. Закон максимального трения для такой модели материала требует, чтобы при проскальзывании удельные силы трения равнялись пределу текучести при чистом сдвиге. Свойство сингулярности сохраняется также в некоторых других моделях жесткопластических тел [3–9]. В работах [4, 5] выполнен общий асимптотический анализ поведения решений вблизи поверхностей максимального трения для выбранных моделей материала, а в [3, 6–9] рассмотрены модельные краевые задачи, включающие условие максимального трения на границе. Поля скоростей, полученные в модельных задачах, являются сингулярными.

Свойство сингулярности поля скорости может быть использовано для описания физических процессов, которые интенсивно протекают в тонком слое вблизи поверхностей трения, изменяя структуру и свойства материала [10–12]. Эти процессы происходят вследствие высоких градиентов поля скорости, и их наличие подтверждается экспериментально [13, 14]. Что касается численных решений, то они не предсказывают сингулярного распределения скорости и изменения свойств в тонком слое материала вблизи поверхностей трения [13, 15]. В связи с этим аналитическое исследование поведения решений вблизи поверхностей максимального трения имеет не только теоретическое, но также и прикладное значение. В частности, полученное асимптотическое представление поля скорости может использоваться в численных схемах для точного описания поведения решения в окрестности поверхностей трения.

Во всех отмеченных выше работах исследуется течение вблизи геометрически гладких поверхностей. Но в некоторых случаях течение материала происходит в окрестности угла, образованного двумя поверхностями трения. В настоящей работе ставится модельная краевая задача, цель решения которой — выявление некоторых особенностей пластического течения в подобных условиях и сравнение качественных особенностей этого решения с решениями других модельных задач, в которых также имеются две поверхности максимального трения, образующие угол [16, 17]. Поставленная задача может рассматриваться как обобщение задачи Прандтля о сжатии идеального жесткопластического слоя параллельными шероховатыми плитами (см., например, [16]), а также ее осесимметричных аналогов: задачи о выдавливании идеального жесткопластического материала из сжимающегося полого цилиндра [16]; задачи об обжатии идеального жесткопластического материала на жесткой оправке [18]. С другой стороны, данная постановка краевой задачи значительно отличается от постановки в работе [19], где исследуется плоское течение при сжатии пластического материала вращающимися плитами.

Здесь рассматривается течение идеально жесткопластического материала между двумя вращающимися шероховатыми плитами. Материал подчиняется условию текучести Мизеса и ассоциированному закону течения. Система определяющих уравнений для этой модели материала приводится, например, в [16].

Предполагается, что на произвольном и достаточно большом расстоянии от оси вращения плит r = r ₀ находится гладкая стенка, препятствующая течению материала в радиальном направлении. Поверхность стенки имеет форму окружности, через центр которой проходит ось вращения плит. Таким образом, материал, деформируемый плитами, может течь вдоль оси z цилиндрической системы координат r 0 z, ось z которой совпадает с осью вращения плит. Плоскость z = 0 совпадает с плоскостью симметрии слоя. Геометрическая схема процесса (сечение плоскостью z = const) показана на рисунке. Ввиду симметрии достаточно получить решение в области z >  0 и 0> 0.

Рис. Геометрическая схема процесса

Кинематические краевые условия задаются на плоскости симметрии ( θ= 0 )

uθ = 0

и на поверхности плиты ( θ=α )

uθ =-ωr.

В этих уравнениях u _θ ― окружная скорость, ω — угловая скорость плиты, α ― половина угла раствора плит. По аналогии с другими модельными задачами такого класса [16, 18] на плоскости симметрии ( z = 0) точное краевое условие замещается интегральным условием, накладываемым на компоненту скорости u z :

∫α∫r0uzz=0rdrdθ=0.(3)

Статические краевые условия на плоскости симметрии ( θ = 0 ) принимаются в виде:

τθz =0, τrθ=0.(4)

На поверхности плиты ( θ=α ) задается закон трения:

(τ2θz+τr2θ) 12=mσs3, m≤1(5)

В уравнениях (4), (5) обозначается: τ _{r θ} и τ_{θ z} ― касательные компоненты тензора напряжения, m — коэффициент трения, σ _s ― предел текучести при одноосном растяжении. Закон максимального трения получается при m = 1 .

Как и в случае кинематических краевых условий, точные статические краевые условия на поверхности z = W , где W — половина ширины слоя вдоль оси z , заменяются интегральным условием вида:

α r 0 2

∫∫ σ _{zz z = W}rdrd θ=- p ⁰⁰ . (6) 00 2

Здесь σ _zz ― нормальное напряжение в направлении оси z , p ₀ ― заданное давление на поверхности z = W (следует заметить, что в постановке Прандтля p ₀ = 0 ).

Полагается, что радиальная скорость равна нулю: u_r = 0 . Тогда компоненты тензора скорости деформации в цилиндрической системе координат выражаются через компоненты вектора скорости u _θ и u_z следующим образом:

ξ rr = 0, ∂ u θ    -1 ∂ u z 2 ξ θ z =∂ z + r ∂θ ,	ξ θθ =	∂ u r -1        , ∂θ Qu	ξ zz =	∂ u
				z ∂ z , ∂ u θ u θ . ∂ rr	(7)
	2 ξ rz	= z ∂ r ,	2 ξ r θ

Для ненулевых компонент вектора скорости используется такая форма записи:

u 9= rU0 (9) , uz = -zU0+ rU1 (9) + Vo, где U0 и U1 — произвольные функции полярного угла; V0 = const; символ «‘» обозначает производную по 9 .

Подстановка компонент вектора скорости (8) в выражения (7) дает соотношения

^ rr = 0,     ^ 99 = U 0 ,    ^ zz = - U ‘ ,    2 ^ 9 z = U ‘ ,    2 2 rz = U„     2 ^ Г 9 = 0,             (9)

из которых видно, что уравнение несжимаемости £ _rr + ^₉₉ z _zz = 0 выполняется при любом выборе функций U ₀ и U ₁ . При условии текучести Мизеса ассоциированный закон пластического течения имеет вид: ^ _у = Хт _у , где T j — компоненты девиатора тензора напряжения, X — неизвестная функция ( Х> 0). С учетом этого из (9) получается:

т rr = 0,    U 0 =XT 99 ,     U 0 =-Xt zz ,    U ‘ = 2 XT 9 z ,     U , = 2 Xt rz ,     т r 9 = 0.         (10)

Из последнего равенства в (10) следует, что второе из краевых условий (4) выполняется автоматически, а условие (5) при 9 = а преобразуется к виду:

|T9z| = m °s/V3.

В силу того, что уравнение несжимаемости уже удовлетворено, из соотношений (10) могут быть получены только два независимых уравнения, не содержащие X :

^T 99 ^-T zz

= 4    ,

U 1

^T 9 z

U

^U 1 ^.

Таким образом, компоненты девиатора тензора напряжения зависят лишь от 9 , и уравнения равновесия в цилиндрической системе координат с учетом равенств (10) записываются в виде:

52-199 = 0     da + ,/:..„ 0      r_, dT9z + r_,т = -5а

dr    r ’     59   d 9     ,          d 9       rz     dz

Здесь ° — среднее напряжение. Так как т₉₉ не зависит от r , то интегрирование первого уравнения системы (13) дает формулу

° = T99 ln ( r/r0 ) + °s °0 (9, z) , где а0 (9, z) — произвольная функция 9 и z. В результате подстановки выражения (14) во второе уравнение системы (13) получается:

^d2 0 ( ⁹ , ^z )

dT^rtln (r!r0) + 1] = -С s d 9

Поскольку правая часть уравнения (15) не зависит от r , то его левая часть тоже не должна зависеть от r . Это возможно только в случае, если т₀₀ = с s A , где A = const. Из равенств (10) и тождества т rr + т₀₀ + т zz = 0 получается

^Т 00 =- ^Т zz = ^С s ^A . ⁽¹⁶⁾

С учетом этого из (15) вытекает, что с ₀ зависит только от z .

С другой стороны, из (14) и условия независимости от r компонент девиатора тензора напряжения следует, что последнее уравнение системы (13) имеет решение только при дс ₀ ( 0 , z )/ 5 z = 0. Отсюда с ₀ = В = const, и выражение (14) с учетом (16) преобразуется к виду:

а/аs = A • In (r/r) + В .

На контактной поверхности нормальное напряжение должно быть отрицательным. Так как компоненты девиатора тензора напряжения ограничены, то из (17) следует, что должно выполняться неравенство A > 0. Тогда из (16) вытекает другое неравенство, т00 > 0 , из которого с учетом (9), (10) и условия X > 0 получается, что ^00 > 0 . То есть, постановка краевой задачи является корректной только при выполнении условия ю < 0 (угол а увеличивается со временем). В этом случае осевая компонента вектора скорости имеет отрицательное значение, и условие трения (11) принимает форму т0z = mаs/V3 .                                                                      (18)

Подстановка (17) в третье уравнение системы (13) приводит последнее к виду:

d ^т 0 z d 0

+ т rz

= 0.

С учетом (10) и (16), условие текучести Мизеса [16] приобретает вид:

T2 + T0z =02(1/3 - A2)

и удовлетворяется подстановкой

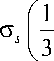
A ² I sin v ,

^T rz

-

с

s

-

. 2 V"

A ² I cos v .

Если принять во внимание граничные условия (4) и условие трения (18), полученное в предположении, что компонента вектора скорости течения материала u_z при ю <  0 имеет отрицательное значение, то естественно предположить, что т_{0 z} >  0 в области 0 <0<а . Но из уравнения (19) следует, что т _rz <  0. Таким образом, из формул (20) получается, что угол v лежит в интервале

Подстановка (20) в (19) приводит уравнение для у к виду d у/ d 6 = 1 и краевому условию у = 0 при 0 = 0, где учтены выражения (4), (20) и (21). Тогда для угла v становится справедливым равенство у = 0 и формулы для касательных напряжений (20) трансформируются в новые:

^т 0 z

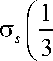
V2

A ² I sin 0 ,

^T rz

I 1     a^V2

— A ² cos 0 .

13     J

После подстановки решения вида (22) во второе уравнение системы (12) получается следующее уравнение для функции полярного угла U‘ /U 1 =- tg 0 . Его общее решение имеет вид:

U 1 = C cos 0 .

Здесь C — постоянная интегрирования. Из (10), (22) и условия X >  0 следует, что U 1 <  0 и, таким образом,

C < 0.

Подстановка выражений (16), (22) и (23) в первое уравнение системы (12) позволяет получить формулу для нахождения функции полярного угла U 0 :

U '=- 1 A • C ^f 1 - A A

⁰      2       ( 3

Из (1) и (8) следует, что при 0 = 0 для функции U ₀ справедливо равенство U ₀ = 0, и решение уравнения (25) имеет вид:

U = — A • C I— A I 0 . 0     2       ( 3 J

Постоянная C определяется из (2), (8) и (26) по формуле:

C = — f 1 - A2)Aal 3    J

.

Так как A >  0 и ю< 0, то выражение (27) согласуется с (24) и константа A определяется из (18) и (22):

A = -1

(

1 -

m

• 2

sin a J

С помощью (23), (26)–(28) поле скорости (8) записывается в другом виде:

rtoO

uO =-- a

z to 2to r • cos Ouz =--1-- a a

" sin2 a

\ -12

-1

+ V o .

Входящая сюда постоянная V ₀ определяется из (3) и (29):

_ 4 r ₀ to • sin a

V o =^-^     2

3 a

< • 2

sin a

\ -12

-1

Теперь из соотношений (16) и (17) легко находится распределение напряжения с ₀₀ , которое является нормальным напряжением на контактной поверхности:

^oo/^, = A + B + Aln(rlro) , где постоянная B вычисляется по формуле

B = — 1 -2

₂     12

m

sin2 a ,

2 ^{p 0}

полученной на основании выражений (6), (16), (17) и (28).

Как видно, c _OO является монотонно возрастающей функцией r . Следовательно, условие отрицательности нормального напряжения на всей контактной поверхности выполняется, если A + B <  0. Это неравенство с учетом выражений (28) и (31) преобразуется к виду:

p > с,

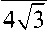
₂     12

m

sin ² a

и ему всегда можно удовлетворить соответствующим выбором величины p ₀ .

Практическая реализация рассмотренного процесса, особенно с учетом того, что to <  0, вряд ли возможна. Поэтому основное значение полученного в настоящей работе аналитического решения состоит в том, что оно точно удовлетворяет всем уравнениям и краевым условиям на поверхностях трения. Решение имеет качественные особенности, отличающие его от других решений краевых задач, также содержащих две поверхности трения, образующие угол. Об этом свидетельствуют приведенные ниже примеры.

Пример 1. Решение, приведенное в работе [16], описывает плоское течение пластического материала через плоский сходящийся канал. В задаче допускается сток материала через точку пересечения поверхностей трения (при плоском течении поверхности трения вырождаются в линии). Эта дополнительная сингулярная точка фактически разделяет две поверхности трения, и асимптотическое поведение решения вблизи каждой поверхности трения следует положениям общей теории, развитой для геометрически гладких поверхностей [2], если принимается закон максимального трения.

Таким образом, наличие точки пересечения поверхностей трения не оказывает влияния на качественное поведение решения вблизи поверхности максимального трения. Этот вывод не совпадает с выводами данной работы.

Пример 2. В работе [17] рассмотрено выдавливание пластического материала из пространства между двумя парами сближающихся параллельных шероховатых плит.

Сечение пластического материала имеет форму квадрата. Из решения следует, что коэффициент m в законе трения вида (5) не может превышать величину 12. То есть, закон максимального трения не может выполняться. Однако если величина m принимается равной 12, то некоторые компоненты тензора скорости деформации стремятся к бесконечности при приближении к угловой точке. При этом на каждой поверхности трения все компоненты скорости деформации всегда конечны.

Как и в работе [17], в публикуемом решении максимально возможная величина m меньше единицы. Из ряда уравнений, например (28), видно, что m <  sin а . В решении [17] угол между пересекающимися поверхностями трения составляет п/2. В этом случае в публикуемом решении — а = п/ 4, и в обоих случаях получается, что m <  1/V2. Однако, несмотря на совпадение, качественное поведение решений различно. Из уравнений (29) следует, что никакие компоненты тензора скорости деформации не стремятся к бесконечности при приближении к углу, где r ^ 0. Кроме того при m ^ sin а некоторые компоненты тензора скорости деформации стремятся к бесконечности во всей пластической области, что лишено физического смысла.

Таким образом, публикуемое решение имеет силу, только если m <  1/V2. Точную максимально допустимую величину m установить нельзя. Приближенная величина, при необходимости, может быть определена из условия, что размер области вблизи плоскости симметрии z = 0, в которой решение не имеет силы (такая область всегда существует для рассматриваемого класса задач, включая задачу Прандтля [16]), достаточно мала. В частности, размер такой области можно найти из условия u_z<  0 и уравнений (29). Необходимо отметить, что из (29) и (30) следует: u z >  0 при z = 0 и r = 0. Расхождение в поведении настоящего решения и решения [17], вероятно, вызвано тем, что в решении [17] не выполняется одно из общепринятых условий для удельных сил трения при проскальзывании: в решении [17] эти силы не направлены против вектора скорости. В связи с этим представляется, что настоящее решение точнее отражает качественные особенности поведения решений вблизи угловой точки пересечения двух поверхностей трения. В частности, можно предположить, что при проскальзывании решение не существует при достаточно больших значениях m , то есть проскальзывание не возникает при использовании закона максимального трения. Следовательно, сингулярные поля скорости также не возникают в окрестности угловой точки, образуемой пересечением двух поверхностей максимального трения. Такое поведение решения аналогично случаю вязкопластического течения, рассмотренному в следующем примере.

Пример 3. Обобщение решения Прандтля на вязкопластические материалы получено в [20]. Из непосредственного анализа этого решения следует, что оно не имеет силы при применении закона максимального трения. Более того, невозможно точно установить максимально допустимую величину m , но ее можно оценить из общих соображений, как и в публикуемом решении. Для модели вязкопластического материала, использованной в [20], известно, что не существует решений при проскальзывании при применении закона максимального трения [21].

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 08-08-90104-Мол-а) и Совета по грантам Президента РФ для ведущих научных школ (грант НШ-134.2008.1).