Технико-экономические и термодинамические аспекты оптимизации лезвийной обработки
Автор: Рыжкин Анатолий Андреевич, Олейникова Юлия Анатольевна, Моисеев Денис Витальевич, Фоминов Евгений Валерьевич
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Машиностроение и машиноведение
Статья в выпуске: 4 (87) т.16, 2016 года.
Бесплатный доступ
Целью данного исследования является разработка расчетного метода выбора оптимальной скорости резания, соответствующей минимальной интенсивности изнашивания инструмента. Выполнен анализ известных критериев оптимизации: трибологических, температурных, энергетических и термодинамических. Выявлены признаки их оптимальности при вариации скорости резания (трения). Особое внимание уделено разработанным в Донском государственном техническом университете экспериментальным термодинамическим критериям оптимизации, отражающим флуктуационную природу трения и износа. Показано, что максимальные значения флуктуационных критериев при вариации скорости резания характеризуют повышенные диссипативные возможности зоны резания. Получена формула для расчета оптимальной скорости резания из условий теплового равновесия на контактных площадках токарного резца. Кроме элементов режима резания, геометрии инструмента и контактных нагрузок в формулу входит деформационная характеристика процесса резания - коэффициент укорочения стружки. Предложенная аналитическая зависимость позволяет выбирать оптимальный режим с помощью расчетов, без проведения дорогостоящих стойкостных экспериментов.
Режимы резания, оптимальная скорость, критерии оптимизации, термодинамика изнашивания
Короткий адрес: https://sciup.org/14250247
IDR: 14250247 | УДК: 621.9 | DOI: 10.12737/22162
Текст научной статьи Технико-экономические и термодинамические аспекты оптимизации лезвийной обработки
Введение. Проблема оптимизации функционирования системы трения и резания имеет как общие, так и специфические особенности.
Главной задачей трибологии деталей машин и механизмов является снижение износа и повышение долговечности пар трения в условиях сухого и граничного трения. В итоге увеличивается срок службы машин и сокращаются затраты на их эксплуатацию. В этой связи решаются задачи снижения потерь на трение — уменьшения его сил и коэффициентов. В данном случае критерием оптимизации служит интенсивность изнашивания при различных скоростях и давлениях.
Развитие машиностроения и металлообработки требует постоянного повышения качества выпускаемых машин. Этому, в свою очередь, способствует использование современного оборудования, технологий, инструмента и систем управления процессами резания.
На современном автоматизированном оборудовании при использовании твердосплавных инструментов уровень скоростей резания на токарных операциях может достигать 500 м/мин. В этих условиях необходимо обеспечить надежность инструментальной наладки в целом и получить заданные выходные параметры системы резания — технологические и экономические. К технологическим относятся: показатели точности обработки и качества обработанной поверхности (шероховатость, степень и глубина наклепа, величина и знак остаточных напряжений); ресурс (стойкость) инструмента. К экономическим показателям относятся производительность и себестоимость обработки.
На операциях формообразования при лезвийной обработке допускаемая скорость является главным элементом режима резания, и оптимальной считается такая скорость VО , которая обеспечивает минимальную интенсивность изнашивания и максимальную стойкость инструмента. В работах А. Д. Макарова, С. С. Силина, В. Ф. Безъязычного, А. Г. Суслова и др. показано, что при скорости резания VО (сечение среза постоянно) обеспечиваются:
-
— минимальные или минимально стабилизированные значения тангенциальной силы резания и высоты неровностей обработанной поверхности;
-
— минимальные глубина наклепа и параметры контактных процессов;
— оптимальная температура резания.
Скорость резания, при которой себестоимость изготовления минимальна, есть экономическая скорость резания VЭ . Скорость максимальной производительности VП — это скорость, при которой обеспечивается максимальная производительность рабочего места. При вариации скорости резания V кривая «производительность — скорость резания» имеет максимум при оптимальной скорости.
О критериях оптимизации процесса контактного взаимодействия в условиях трения и резания. Методам выбора оптимального режима резания (критериев оптимизации) посвящено значительное количество научных работ. Большая их часть рассмотрена в [1–5]. Приведем дополнительно материалы исследований последних лет (табл. 1), условно объединив их в следующие группы: трибологические (механофизические), тепловые, энергетические и термодинамические.
Критерии оптимизации процесса резания
Таблица 1
|
№ п/п |
Группа критериев |
Содержание критерия оптимизации |
Признак оптимальности при вариации скорости трения (резания) |
Примечание |
Источ-точ-ник |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1. |
Трибологические |
1. Коэффициент трения f |
f → min |
h — линейный износ, τ — время |
[1–3] |
|
2. Сила трения F |
F → min |
||||
|
3. Износ h |
h → min |
||||
|
dh 4. Скорость износа d τ |
dh → min d τ |
||||
|
5. Интенсивность изнашивания J |
J → min |
||||
|
2. |
Тепловые (температурные) |
6. Приращение температуры резания при Lрез . |
∆ T ( ∆ E ) = f ( V ) ∆ T ( ∆ E ) → min |
T — температура, E — термо-ЭДС |
[4] |
|
7. Равенство температур (термо-ЭДС) на контактных площадках |
T ПП = T ЗП ( EПП = EЗП ) |
T ПП ( E ПП ), T ЗП ( E ЗП ) — температуры (ЭДС) на передней и задней поверхностях |
[5] |
||
|
8. Разница твердости HRC 1 – HRC 2 |
θ = f ( V ) ∆ HRC = max |
θ — температура как функция скорости резания; HRC 1 и HRC 2 — твердости инструментального и обрабатываемого материалов |
[6] |
||
|
9. Точка перелома кривой «твердость HV — температура» |
lg HV = f ( θ п ) θ = f ( V ) |
θ п — температура точки перелома |
[7] |
|
10. Оптимальная скорость резания V _ к 2 х С Р .« 10 ' (, ^ + 4(sin α)0,1 Pz + 2,6й р ве(в ; ) 0'3 , K 2 a 2 b 2λ с ρ E 0,25 (sinα)0,065 |
По P z min определяется оптимальная температура θ |
θ — температура резания, Pz min — минимальное или минимально стабилизированное значение силы Pz |
[8] |
||
|
3. |
Энергетические |
11. Отношение общих энергозатрат процесса к единице объема удаленного материала U PV п = = 1 VST VST |
П i ^ min |
S — подача, t — глубина резания |
[9] |
|
12. Отношение тепловой активности стружки к теплоте резания A _ VStc р T _ Stc р T P z V P z |
A ^ min |
с ρ — удельная объемная теплоемкость стружки, T — температура резания |
[10] |
||
|
13. Приращение силы резания от времени износа инструмента W„ APV т e _ —= _ —z— W PzV τ WW e„ _ ; e _ и V и V |
e ^ min |
A P Z p PT - Po — приращение силы PT за время τ; W и — энергия, затрачиваемая на износ; W — энергия, затрачиваемая на процесс резания; V и — объем изношенной части инструмента; V — объем снятой стружки |
[11] |
||
|
14. По совокупности термодинамических параметров процесса резания W G _ __ p _ _ пп VT |
Расчет G для различных обрабатываемых материалов: G_f (V ), при G _ const оценивается V о |
Wp — мощность резания; V — объем срезаемого слоя |
[12] |
||
|
4. |
Термоди-намиче-ские |
15. Аналог производства избыточной тепловой энтропии ~ ~ Ks _ - ; K _ - S E ε E |
Ks ^ min K e ^ min |
E — постоянная термо-ЭДС пары «инструмент — деталь»; e — переменная термо-ЭДС; св — мощность переменной составляющей термо-ЭДС |
[1–3, 5] |
|
Характеристики мощности флуктуаций |
|||||
|
~ ~ ~ — 16. N _ PzV , N _ PzV |
N _ PzV ^ max |
Pz — переменная составляющая тангенциального усилия P z ; V — виброскорость линейных перемещений резца; S — аналог производства тепловой энтропии в микрообъемах изнашива емого материала; N — мощность флуктуаций; KN — коэффициент использования мощности флуктуаций |
[1, 13] |
||
|
~ ~ ~ N P У 17. KN — _ z N N PzV |
~ ~ PV KM _ —z-- > max N P z V |
||||
|
~ ~ PV - P У 18. S _ p z — ; S _ pz— e E |
~ ~ PV S _ —--> max ε |
||||
|
~ ~ PV e ( pzV ) 19 S ε . S S P z — E |
~ S Ks = > max S S |
В таблицу не включены технологические критерии оптимизации, т. к. они достаточно широко представлены в исследованиях С. С. Силина, В. Ф. Безъязычного, А. Д. Макарова, А. Г. Суслова и были проанализированы ранее [2, 5, 14].
Как следует из представленных в табл. 1 данных, известные критерии оптимизации на оптимальной скорости соответствуют минимальной интенсивности изнашивания, имеют экстремальные значения: — критерии 1–5, 6, 11–13, 15 (см. графу 3 табл. 1) — минимальные;
— критерии 8, 16–19 — максимальные;
— остальные (9, 10 и 14) связаны с изменением характеристик материала от температуры и нахождением оптимальной скорости по зависимости «температура — скорость резания».
Разработанные в ДГТУ термодинамические критерии оптимизации 16–19 (см. табл. 1) отражают флуктуационную природу трения и износа, условия диссипации энергии трения и доминирующую роль тепловых процессов в изнашиваемом инструментальном режущем материале. Флуктуации тангенциальной силы резания Pz , скорости V и переменной составляющей термо-ЭДС ё отображают флуктуации тепловой мощности и температуры и являются источниками негэнтропии относительно зоны контакта, где имеет место накопление энтропии и износ материала. При этих условиях комплексы N , KN , S и KS максимальны. В этом случае система резания (трения) характеризуется повышением диссипативных возможностей контакта, из-за чего уменьшается накопление энтропии в объеме и снижается износ.
Заметим, что рассмотренные критерии оптимизации основаны на использовании экспериментальных данных по интенсивности изнашивания и их соответствии «конструированным» комплексам механофизической, энергетической и термодинамической природы. Для оптимального управления процессом износа необходимо иметь аналитические зависимости для оценки оптимальной скорости (или другого управляющего параметра). Известны зависимости С. С. Силина [8] (см. строку 10 табл. 1) и А. А. Рыжкина по расчету оптимальной подачи [5], полученные из уравнения теплового баланса зоны резания. В настоящее время требует уточнения подход к расчету оптимальной скорости с позиции термодинамики необратимых процессов.
Расчетный термодинамический метод выбора оптимального режима резания при точении. Ранее сформулированы [5] термодинамические условия, при которых система резания, функционирующая в условиях интенсивного тепловыделения, «выходит» на оптимальный режим. В качестве критериев оптимизации были приняты следующие термодинамические характеристики:
-
— равенство температур на передней и задней поверхностях инструмента — ТПП = ТЗП ;
-
— равенство суммарных ( QПП = QЗП ) и удельных ( qПП = qЗП ) тепловых потоков через контактные площадки ин-
- струмента;
равенство тепловых энтропий на передней и задней поверхности инструмента qПП = qЗП ).
Т ПП Т ЗП
Q ПП Q ЗП
SПП = SЗП ( = ;
Т ПП Т ЗП
В формулах, полученных на основе уравнения теплового баланса [5], учитывались все возможные схемы движения тепловых потоков через зону резания. Такое усложнение оказалось излишним. Наш многолетний опыт расчета оптимальной скорости резания по этим зависимостям показал, что ряд коэффициентов распределения второсте- пенных тепловых потоков аналитически оценить затруднительно.
Примем упрощенную схему тепловых потоков на передней и задней поверхностях резца. При этом через коэффициенты b* и (1 – b* ) учтем соответственно теплоты от трения и доли тепла деформации, уходящие в стружку и обработанную деталь (рис. 1).
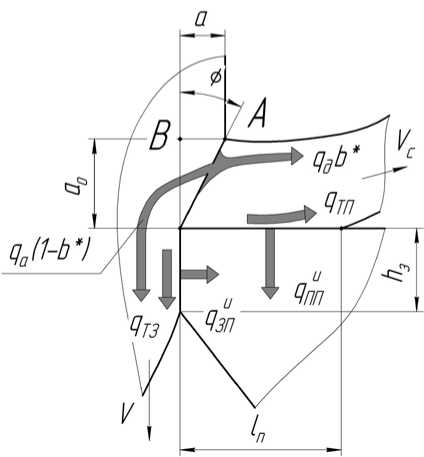
Рис. 1. Упрощенная схема действия тепловых потоков на контактных площадках резца
Рассмотрим один из вариантов решения контактной тепловой задачи, приняв в качестве условия оптимизации баланс плотностей тепловых потоков на контактных площадках инструмента:
q nn = q 3n , q nn = q * + q Tn , q g = т ф ■ V g ■ b * .
*
Здесь qд — теплота деформации; b * — доля тепла деформации, ушедшего в стружку; τ ф — напряжение сдвига в
cosγ плоскости ОА (см. рис. 1); Vg = V-------- — скорость сдвига; V — скорость резания; 0 — угол сдвига; y — перед- cos(0 - у)
ний угол.
cosγ
Приняв A =-----!— , получим:
cos(0 - у)
q g = т ф ■ V g ■ b * = A ■ т ф ■ V ■ b * .
Плотность теплового потока от трения по передней поверхности: q Tn = т F ■ V c ,
V где: тр — касательное напряжение на передней поверхности; V =-- — скорость движения стружки; K — коэф-
F c K a a
фициент утолщения стружки. В итоге:
_ т F ■ V qTn = -7Г- K a
.
Из (2), (4) и (6) получим:
τ qnn = qg+ qTn = V(A ■т ф ■ b *+ -). Ka
Плотность теплового потока по задней поверхности резца:
q 3n = q g (1 - b*) + q T3 = A т ф (1 - b*) + т зп V = V ( A т ф (1 - b *) + т зп )
Здесь τ ЗП — касательное напряжение на задней поверхности резца; (1 – b* ) — доля тепла деформации, ушедшего в деталь.
Приравняем правые части выражений (7) и (8):
V ( A т ф (I - b *) + т ЗП ) = v ( A т ф Ь * + Те- ).
Ka
Коэффициент b* определяется по известной зависимости [5]:
VS ■ sin ф
1,33Ka 6a2 sin 0 + Vv ^S ■ sin ф где S — подача, φ — главный угол в плане резца, a2 — коэффициент температуропроводности обрабатываемого мате- риала.
Обозначая B = ^ sinф , С = 1,33^6 a 2 sin0 и подставляя (10) в (9), получим:
τ F
A т ф K a + т ЗП = b V S W
2 A т ф bJSJv + CKa '
Решение (11) относительно S дает:
^ = C ( K a 2( A т ф + т ЗП ) - т F К д ) B W( K a ( A т ф - E т ЗТ ) + т ф ) .
Если (11) решить относительно V , получим:
^V = C ( K a 2( A т ф + т ЗП ) - т F К д ) B V S ( K a ( A т ф - E т ЗТ ) + т ф ) .
О связи оптимальных режимов резания с деформационными процессами при резании. В формулы для расчета оптимальных скоростей резания (13) кроме напряжений τф, τF, τз, угла сдвига, теплофизических свойств материала заготовки входит и коэффициент укорочения (усадки) стружки Ka. Очевидно, для расчета скоростей параметр Ka должен иметь экстремальные значения, и для этого необходимо учитывать функциональные зависимости Ka от параметров процесса резания.
Согласно результатам работы [15], зависимость Ka от скорости резания может быть аппроксимирована кривой вида:
K a = aYbecV , (14)
где: V — скорость резания; a, b и c — постоянные коэффициенты.
Имея массивы данных величин Ka при изменении скорости резания V , пользуясь известной методикой [15–17], находили постоянные a, b и c в зависимости (14).
Так, при точении стали 45 резцами Т15К6 ( t = 0,5 ■ IO - 3 м, S = 0,23 ■ IO - 3 м/об.) для скоростей резания 0,97; 2; 3 и 4,5 м/с получили значения коэффициентов K a , равные 3,4; 2,9; 2,55 и 2,4 соответственно. Для этого случая уравнение (14) будет иметь вид: K a = 1,26 V 0,48 e - 0,54 v .
В табл. 2 представлены некоторые результаты обработки экспериментальных данных.
Результаты оценок параметров кривых K a = aYbecV для различных условий точения
Таблица 2
|
№ п/п |
Пара «инструмент — деталь» |
Подача S ■Ю - 3 м/об. |
Уравнение для оценки K a |
Точка перегиба на кривой Ka |
|
|
K aп |
V п |
||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
Т15К6 — сталь 45 |
S = 0,14 |
Ka =5,73V 1,49 e –0,69V |
2,94 |
3,9 |
|
( t = 0,5 ■ IO - 3 м; V = 1,0 - 4,5 м/с; |
S = 0,23 |
Ka =1,26V 0,42 e –0,54V |
2,97 |
2,17 |
|
|
φ = 35º; γ = –5º) |
S = 0,43 |
Ka =3,2V 1,62 e –1,92V |
2,8 |
1,5 |
|
|
2 |
ВК8-12Х18Н10Т ( t = 0,5■Ю - 3 м; V = 0,34 - 2,14 м/с; |
S = 0,23 |
Ka = 3,37V 0,88 e –0,41V |
1,89 |
1,09 |
|
φ = 45º; γ = –5º) |
|||||
Изменения коэффициентов усадки стружки от скорости резания для точения стали 12Х18Н10Т сплавом Т15К6 и ВК8 представлены на рис. 2 и 3, для пары «Т15К6 — сталь 45» — на рис. 4.
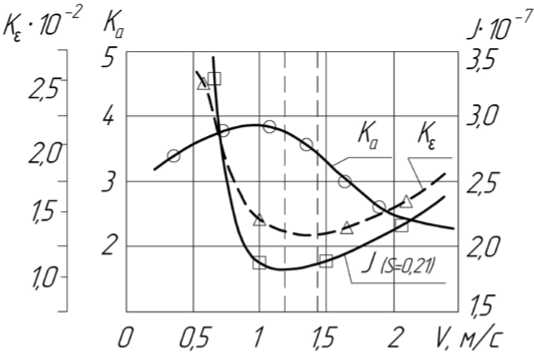
Рис. 2. Влияние скорости резания на усадку стружки при продольном точении стали 12Х18Н10Т резцом из Т15К6
( t = 0,5 ■ 10 - 3 м; S = 0,23 ■ 10 - 3 м/об.; ф = 45°; y = -5°)
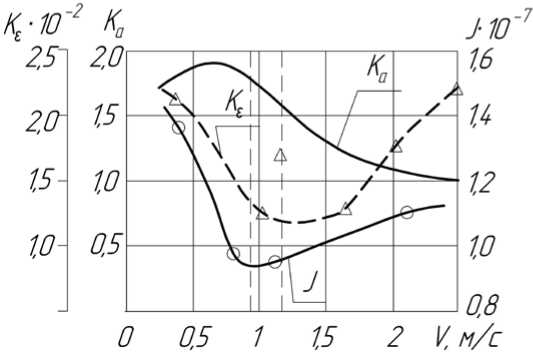
Рис. 3. Влияние скорости резания на усадку стружки при продольном точении стали 12Х18Н10Т резцом из ВК8 ( t = 0,5 ■ 10 - 3 м; S = 0,14 ■ 10 - 3 м/об.; ф = 45°; y = -5°)
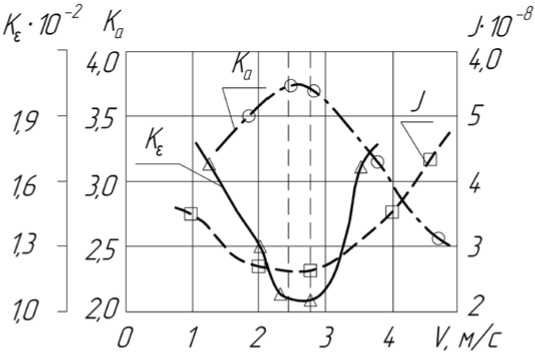
Рис. 4. Влияние скорости резания на усадку стружки при продольном точении стали 45 резцом из Т15К6 ( t = 0,5 ■ 10 - 3 м; S = 0,11 ■ 10 - 3 м/об.; ф = 35°; у = -5°)
На рис. 2-4 кроме кривых K a = f (V ) представлены результаты исследований авторов данной статьи по интенсивности изнашивания резцов (кривые J = f ( V ) и изменение термодинамического критерия оптимизации K § = f (V )).
Полученные данные показывают следующее. Скорость резания, соответствующая точке перегиба кривой K a = f (V ) (правая вертикальная пунктирная линия на рис. 2-4), является оптимальной, так как ей соответствует минимум на кривой J = f ( V ) (левая вертикальная пунктирная линия на рис. 2-4).
Полученные зависимости для расчета усадки стружки вида K a = aVbecV (14) могут быть использованы для расчета оптимальных скоростей резания.
Какие значения Ka следует вводить в зависимость (13)? Очевидно, речь должна идти об экстремальных значениях этого параметра, оцениваемого обычно значениями первой и второй производной функции, в данном случае (14).
Найдем К'а и K"a :
K a = a [V b ce cV + bV b - 1 e cV ] = ae cV ( bV b - 1 + cV b ), K" Q = ae cV { C [ V b c + bV b - 1 ] + b [ V b - 1 c + ( b - 1) V b - c ]}.
Положим K'a = 0 . В (15) сомножитель ae cV * 0 , тогда:
{ c [ V b c + bV b - 1 ] + b[V b - 1 c + ( b - 1) V b - c ]} = 0 .
После преобразований (16) получим:
V c + — V + -^- ( b - 1) = 0, откуда c c c
^ /a c c c - c c b ( b - 1)
V =
c c
или
V =
= V .
c
Таким образом, при этом значении скорости вторая производная обращается в ноль, а наибольшее значение скорости V = Vn соответствует точке перегиба кривой Ka = f (V ) [16].
Для расчетов оптимальной скорости резания (или подачи) по (13) и (1С) в функцию Ka следует ввести ско-
рость Vп . В общем виде, приняв абсолютные максимальные значения дроби
ь + bb
c
, получим:
Ka = aVbecV = a( b±^)bec( b±^) = a[(-b±7b)c-1]be-b±^ cc b _ b или Ka = a[(bb + b c)c-be c ], откуда:
b b - 3 b
Ka = ab c ( b c + 1) c - b e c .
Для простоты расчета целесообразно использовать экспериментальные соотношения типа приведенных в табл. 2, куда следует ввести расчетные значения Vп и Kan (см. графы 5 и 6 табл. С), используя в дальнейшем этот параметр в формулах (13) или (12).
Пример: рассчитать оптимальную скорость резания при обработке стали 45 резцом Т15К6: у = -5°; 0 = С3,7 ° ;
Ф = 35°; S = 0,14■Ю-3м/об.; V = 3,14м/с; V = 3,9С м/с; Ka = С,94; A = _c£s^ = 1,13; в = £)Пф = 0,76 ; э п aп cos(0 - y)
с = 1,3376 0 с sinф = 0,58 ■ 10 С ; т ф = 867 ■ 10 6 Па, т F = 443 ■ 10 6 Па, т з = 867 ■ 10 6 Па — касательные напряжения в плоском сдвиге на передней и на задней поверхностях резца.
V =
0,59 ■ 10 - С (С, 94 С ■ (1, С3 ■ 867 + 150) - 443 ■ С, 94) ■ 10 6
50С9
0,75 ■ V0,14 ■ 10 - 3 ■ (С, 94 ■ (1,13 ■ 867 - 150) + 4,43 ■ С, 94) ■ 10 6 С951
= 1,7,
откуда V = С,9 м/с.
Экспериментально найденная скорость V = 3,14 м/с, а ошибка по отношению к Vo = С,9 м/с составляет 7,6С %.
Удовлетворительные результаты получены и для расчетных подач. Подсчитав в (22) исходные данные примера для оценки V , имея ввиду, что Vn = 3,9С м/с, Kaп = С,94, нашли So = 0,1 - 10 - 3 м/об.( Sэксn . = 0,14 ■ IO - 3 ).
Выводы.
-
1. Из условия термодинамического равновесия зоны резания при лезвийной обработке, соответствующего равенству плотностей тепловых потоков на контактных площадках, получены расчетные формулы для определения оптимальной скорости резания (подачи).
-
2. В качестве критерия оптимальности в формулу входит усадка стружки. Методом графоаналитической обработки экспериментальных данных получены аппроксимирующие кривые Ka = f ( V ) в виде Ka = aV b e cV , вторые производные которых, приравненные к нулю, есть скорости, соответствующие точке перегиба на кривых Ka = f ( V ) — т. е. оптимальные скорости резания.
-
3. Предложенные аналитические зависимости позволяют выбрать оптимальный режим резания с помощью расчетов, не проводя дорогостоящих стойкостных экспериментов.
-
4. В качестве контроля можно воспользоваться данными по изменению критерия K ε , что не требует больших материальных затрат. Минимум K ε при вариации скорости соответствует точке перегиба кривой Ka = f ( V ) и минимуму износа.
Список литературы Технико-экономические и термодинамические аспекты оптимизации лезвийной обработки
- Рыжкин, А. А. Термодинамические критерии оптимизации процесса изнашивания/А. А. Рыжкин//Надежность и эффективность станочных и инструментальных систем: сб. науч. тр. -Ростов-на-Дону: Изд. центр ДГТУ, 1993. -С. 3-16.
- Рыжкин, А. А. Физические основы обработки материалов резанием/А. А. Рыжкин, К. Г. Шучев, М. М. Климов. -Ростов-на-Дону: Изд. центр ДГТУ, 1996. -342 с.
- Ryshkin, A. A. Optimization of Metal Cutting Conditions/A. A. Ryshkin, L. S. Vorovich, B. I. Gordienko. -Radom: The Institute for Terotechnology, 2000. -315 p.
- Способ определения оптимальной скорости резания: а. с. 657918 СССР/А. Д. Макаров . -№ 233161/08; заявл. 03.03.76; опубл. 28.04.79, Бюл. № 15. -5 с.
- Рыжкин, А. А. Обработка материалов резанием: физические основы/А. А. Рыжкин. -Ростов-на-Дону: Изд. центр ДГТУ, 1995. -291 с.
- Выбор режимов резания труднообрабатываемых жаропрочных интерметаллидных сплавов тепловизионным методом/И. В. Анухин //Станки, инструмент. -2015. -№ 1. -С. 16-20.
- Способ определения оптимальной скорости резания твердосплавного инструмента: патент 2173611 Рос. Федерация: С2 B23 B1/00/Е. В. Артамонов . -№ 99121439/02; заявл. 12.10.99; опубл. 20.09.01, Бюл. № 17. -5 с.
- Силин, С. С. Метод подобия при резании металлов/С. С. Силин. -Москва: Машиностроение, 1979. -152 с.
- Старков, В. К. Дислокационные представления о резании металлов/В. К. Старков. -Москва: Машиностроение, 1979. -160 с.
- Силин, С. С. Оптимизация операций механической обработки по энергетическим критериям/С. С. Силин, А. В. Баранов//Станки, инструмент. -1999. -№ 1. -С. 16-17.
- Тавстюк, А. А. Применение удельных энергетических параметров при оптимизации и управлении процессом резания/А. А. Тавстюк, А. Г. Лютов, Г. Н. Коуров//Станки, инструмент. -2014. -№ 2. -C. 29-34.
- Закураев, В. В. Оценка условий оптимального режима резания по энергетическим характеристикам процесса/В. В. Закураев, С. И. Хадеев. -Новокузнецк: Межотраслевой НТК, 2007. -187 с.
- Рыжкин, А. А. Способ определения оптимальной скорости резания: патент 2521943 Рос. Федерация: B23B1/00/А. А. Рыжкин . -№ 2012105415/02; заявл. 15.02.12; опубл. 10.07.14, Бюл. № 19. -7 с.
- Рыжкин, А. А. Теплофизические процессы при изнашивании инструментальных режущих материалов/А. А. Рыжкин. -Ростов-на-Дону: Изд. центр ДГТУ, 2005. -312 с.
- Виноградов, А. А. Определение оптимальной скорости резания по коэффициенту усадки стружки/А. А. Виноградов//Станки, инструмент. -1991. -№ 7. -С. 32-33.
- Бронштейн, И. Н. Справочник по математике для инженеров и учащихся втузов/И. Н. Бронштейн. -Москва: Физматгиз, 1962. -608 с.
- Грановский, Г. И. Обработка результатов экспериментальных исследований резания металлов/Г. И. Грановский. -Москва: Машиностроение, 1982. -112 с.


