Технологические инновации в области моделирования физических процессов

Введение. Создание суперкомпьютеров, а также разработка систем для проведения исследований, связанных с решением серьезных задач как во всех областях физики, так и в других отраслях науки и техники, оказывает прямое влияние на развитие всей экономики страны. К областям применения высокопроизводительных вычислений относятся масштабные задачи, такие как задачи аэродинамики, газодинамики, атомной промышленности, расчеты турбины реактивного двигателя и др., требующие больших вычислительных ресурсов.

В качестве вычислительных платформ используются кластеры на базе таких технологий такие как MPI (massage passing interface), CUDA (Compute Unified Device Architecture) и Open MP (Open Multiprocessing) [1, 2].

Вычисления могут производиться двумя способами либо как параллельная обработка, либо как конвейерная. Конвейерная обработка означает, что вычисляющие устройства на процессоре могут обрабатывать несколько последующих операций в виде конвейера, в порядке очередности.

Параллельная обработка осуществляется за счет того, что вычислительные узлы соединяются в одну большую систему и могут вести параллельную обработку данных, в то время как конвейерная обработка делается внутри одного кристалла на одном процессоре.

Технологические инновации. В настоящее время архитектуры персональных компьютеров позволяют создавать вычислительные комплексы большой производительности для моделирования и визуализации, используя технику распределенных систем и параллельных вычислений.

Все это стало возможным благодаря открытию и широкому изучению свойств полупроводниковых материалов [3]. Сегодня некоторые полупроводники содержат миллиарды транзисторов и их функциональность реализована не только в компактных современных смартфонах, но и во многих миниатюрных smart-устройствах. Полупроводниковые технологии произвели промышленную революцию и оказали существенное влияние на важнейшие отрасли промышленности, такие как оборонная промышленность, электроника, телекоммуникации и др. Темпы развития полупроводниковой технологии были установлены Гордоном Муром в 1965 году [4], а Дэн Хатчесон подсчитал, что в 2014 году было произведено 7,6 триллиона транзисторов за одну секунду (рис.1).

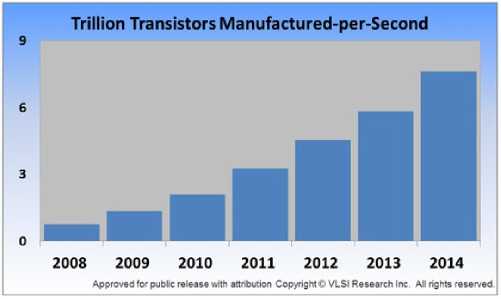
Рисунок 1. Производство транзисторов в секунду

В 2016 году группа ученых под руководством профессора Массачусетского технологического института материало- ведения и инженерии Геофри Бич документально установила наличие скирмионов – квазичастиц, расположенных на поверхности некоторых материалов. Основные свойства этих «частиц» – это устойчивость к внешним возмущениям, это большая плотность и длительность хранения информации [5].

Все эти работы и исследования ведутся для того, чтобы создать высокопроизводительные системы для решения специфических сложных задач, на которые будет затрачено меньше времени и меньше электроэнергии.

Методы моделирования и оценка эффективности. Математическое моделирование некоторых физических объектов решается с помощью вариационных методов, разновидностью которых является метод конечных элементов. Этот метод подходит для решения задач теории упругости, механики жидкости. Главным достоинством метода конечных элементов является индифферентность в отношении геометрии рассматриваемой области, краевых условий задачи, законов изменения свойств среды и внешних воздействий на область. Другие математические модели, описывающие физические явления, основываются на ряде предположений, касающихся состояния объектов, зависимостей от времени и других условий среды. К примеру, расчет движения газа в камере вращения был выполнен с помощью решения дифференциального уравнения методом Рунге-Кутты, а на рисунке 2 показано распределение давления в виде изолиний и распространение скорости газа в виде векторных полей [6].

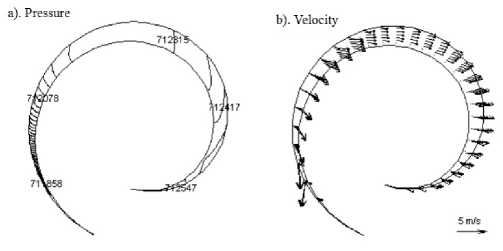
Рисунок 2. Давление и скорость газа в камере

Такие физические процессы, как волновые, можно описывать уравнением Шредингера (1):

--V 2 Y + U ( x , y , z , t ) ¥ = ih .

2 m           ,        ’         912              (1), где m - масса частицы, i - мнимая единица, V - оператор Лапласа, U(x,y,z,t) – потенциальная энергия частицы в силовом поле, в котором она движется, Ψ – искомая волновая функция. Решение подобных задач с помощью уравнения Шредингера стало возможным только с появлением суперкомпьютеров.

Расчеты по изменению климата также производились с помощью суперкомпьютеров, производительность которых позволила десять лет модельного времени просчитать за сутки реального времени. Для этих расчетов использовался кластер на базе процессоров Intell Itanium 2, производительностью примерно 80 гигафлоп (миллиард операций с плавающей запятой в секунду), состоящий из 8-ми двухпроцессорных вычислительных узлов, тактовой частотой 1,3 ГГц. Каждый узел располагал оперативной памятью, емкостью 2 ГБ, и дисковой подсистемой, емкостью 36 ГБ [7].

Таким образом, можно выделить следующие основные этапы моделирования физических процессов. Так как, правильные физические модели должны удовлетворять критериям сходства, которые включают не только условия геометрического сходства, но и сходства многих других характеристик (например, температура, сила, электромагнитное поле, давление и др.), то моделирование любых физических явлений необходимо начинать с постановки и решения задач компонентов физической системы.

Система в широком смысле – это эквивалент понятия математической модели и задается парой множеств { U, Y } (где U – множество входов, Y – множество выходов) и отношением U/Y , формализующим связь (зависимость) между входами и выходами.

Таким образом, можно определять сколь угодно сложные системы, исходя из простых.

Свойства системы – целостность и структурированность. Целостность (единство) означает, что система отделена от внешней среды; среда может оказывать на нее действие через входы и воспринимать отклик на эти действия через выходы.

Структурированность означает, что система разделена внутри на несколько подсистем, связанных и взаимодействующих между собой также, как целая система взаимодействует с внешней средой. Функционирование системы – это процесс, разворачивающийся во времени, т.е. множества возможных входов и выходов U, Y – это множества функций времени со значениями соответственно в множествах { U, Y…. }.

Система называется функциональной (определенной), если каждой входной функции u(t) соответствует единственная выходная функция y(t) . В противном случае система называется неопределенной. Неопределенность обычно возникает из-за неполноты информации о внешних условиях работы системы.

С учетом того, что многие исследовательские институты решают задачи, связанные с моделированием, то необходимо опираться на уже имеющиеся решения, на соответствующий математический аппарат и технологии параллельного программирования, на накопленный экспериментальный материал. Например, системы уравнений, действующие в жидкости или газе, большая их часть которых была получена в гидромеханике, а впоследствии оказались применимы в геофизических задачах.

Выделить основные законы физики, отражающие суть физических процессов, протекающих в системе. К примеру, это может быть закон сохранения вещества, второй закон Ньютона и др. Следующим шагом является обоснование и выбор системы координат: декартова, сферическая, изобарическая и т.д. Далее составить системы уравнений для физической среды. Для получения более точных результатов возможно использование динамических моделей или гибридных. В ряде случаев можно упростить системы уравнений, пренебрегая некоторыми ее членами. Критерии подобия – это характеристики соотношения величин, которые можно использовать для разработки теоретических моделей и анализа результатов, полученных путем численного моделирования. Такими критериями могут быть числа Рейнольдса, Тэйлора, Фруда, Рэлея. Суть их заключается в соотношении между некоторыми параметрами системы.

Для программной реализации полученных систем уравнений существует множество технологий параллельного программирования, ориентированных на использование различных процессорных архитектур и организации оперативной памяти суперкомпьютера.

Основным критерием моделирования физических процессов является вычислимость программ. Для этого существует класс частично-рекурсивных функций, который рассматривается в качестве математического уточнения понятия вычислимой функции натурального аргумента (т.е. функционально-вычислимой с помощью алгоритма. Это утверждение называется тезисом Черча. Кроме этого, другие уточнения классов, вычислимых с функций, полученные Тьюрингом, Постом, Марковым, трактуются как эквивалентные.

Одним из важнейших критериев оценки алгоритмов является их временная эффективность. Если есть несколько функционально эквивалентных алгоритмов, то вероятностная оценка не позволяет сделать обоснованный вывод. В этом случае эффективной оценкой может быть статистическая оценка. Временную эффективность алгоритма необходимо оценивать по его возможным реализациям.

Временная эффективность алгоритма – это функция

E = f ( v , У , x W, r )

(2),

где v – объем, t – тип, x – значения входных данных,

– программная среда функционирования и создания *.exe файла, r – архитектура компьютера.

При наличии нескольких функционально-эквивалентных алгоритмов следует сравнить функции Е1, Е2, …, Еn. Для сравнения временной эффективности 2-х алгоритмов необходимо определить:

– насколько в среднем один из алгоритмов превосходит другой;

– во всей ли исследуемой области наблюдается превосходство, если нет, то как соотносятся размеры областей превосходства каждого алгоритма;

– каким будем превосходство одного из алгоритмов в заданном пределе (по объему данных).

Эффективность параллельной программы определяется как отношение ускорения к числу использованных процессоров E = R/n . Эта величина обычно выражается в процентах. Где R – это параллельное ускорение программы, которое вычисляется как R = T1/Tn , где T1 – время выполнения программы на одном процессоре (вычислительном ядре), Tn – время ее выполнения на n процессорах.

Говорят, что программа ускоряется (или масштабируется) линейно, если эффективность мало меняется с ростом n. Ускорение и эффективность – наглядные понятия, и они часто используются при характеристике работы параллельных приложений, однако, не дают информации о производительности программы в терминах скорости вычислений [8-10].

Заключение . Современные тенденции в разработке вычислительных систем сопровождаются существенными изменениями в их архитектуре, что требует разработки хорошо масштабируемых вычислительных алгоритмов для использования на большом количестве процессорных ядер.

На сегодняшний день в Казахстане имеется несколько суперкомпьютерных центров и моделирование природных явлений и физических процессов играет важную и стратегическую роль в науке и экономике.