Технология дистанционного проектирования робастного интеллектуального управления автономным роботом. Ч. 1: применение оптимизатора баз знаний на мягких вычислениях

В последние годы для проектирования интеллектуальных систем управления (ИСУ) наблюдается активное использование платформы нечетких систем на основе мягких вычислений. Существенным недостатком таких систем является отсутствие стандартной методики конструирования баз знаний (БЗ) нечетких систем управления. Одной из основных проблем эффективного применения технологии мягких вычислений в задачах управления являлось решение следующих задач:

• -    объективное определение вида функции принадлежности (ФП) и ее параметров в продукционных правилах в БЗ;

• -    определение оптимальной структуры нечетких нейронных сетей (ННС) в задачах обучения (аппроксимация обучающего сигнала с требуемой (заданной) ошибкой и с минимальным количеством продукционных правил в БЗ – проектирование универсального аппроксиматора);

• -    применение генетического алгоритма (ГА) в задачах многокритериального управления при наличии дискретных ограничений на параметры объекта управления (ОУ) с целью согласования причинно-следственных связей в продукционных правилах.

Перечисленные проблемы были решены и апробированы на основе Оптимизатора Баз Знаний (ОБЗ) с применением технологии мягких вычислений [1]. Разработанный интеллектуальный инструментарий позволил проектировать робастные БЗ на основе решения одной из алгоритмически трудно решаемых задач теории искусственного интеллекта – извлечения, обработки и формирования объективных знаний без использования экспертных оценок. В данном оптимизаторе используются три ГА, которые позволяют спроектировать оптимальную структуру нечеткого регулятора (вид и число ФП, параметры ФП, а также число самих правил нечеткого вывода), аппроксимирующей обучающий сигнал с требуемой ошибкой.

При этом автоматически проектируется оптимальная структура ННС и формируется модель универсального аппроксиматора в виде нечеткого регулятора с конечным числом продукционных правил в БЗ.

В данной работе рассматривается технология дистанционного проектирования робастных ИСУ (на основе удаленного соединения с ОУ) для настройки БЗ нечеткого регулятора (НР) на основе ОБЗ с применением технологии мягких вычислений. Такая возможность позволяет проектировать ИСУ без использования системы стохастического моделирования, что дает преимущество при проектировании нечетких систем управления для сложных и слабо формализованных ОУ в непредвиденных ситуациях управления.

Кроме того, дистанционная настройка БЗ дает возможность максимально адаптировать нечеткую систему управления для конкретной (непредвиденной) ситуации управления не зависимо от времени и места нахождения ОУ. Такого рода самоорганизующиеся ИСУ с дистанционным проектированием БЗ важны для ликвидации последствий аварий на АЭС, при разборе завалов при землетрясениях, крушении поездов, для работы в загрязненной и радиоактивной окружающей среде и т.п.

Структура и основные функции ОБЗ

Применительно к проектированию ИСУ, мягкие вычисления представляют собой комбинацию из следующих подходов: теория нечетких системы, ГА и ННС.

НР является центральным элементом ИСУ и вырабатывает управляющие сигналы изменения во времени (законы управления) коэффициентами усиления k _p , k _d , k _i ПИД-регулятора. Ядро НР основано на процессе проектирования БЗ, которая интегрирована в интеллектуальный контроллер. Структурно БЗ состоит из продукционных логических правил, которые включают нечеткие входные и выходные значения ФП лингвистических переменных.

Функциональная структура ИСУ с блоками НР и ОБЗ на мягких вычислениях представлена на рис. 1.

Такая структура включает одновременно следующие качества управления: управляемость, точность и устойчивость (нижний уровень управления – САУ) и обучение и адаптация (верхний интеллектуальный уровень управления – НР с БЗ).

Наиболее актуальной проблемой при создании ИСУ является получение оптимальной и робастной БЗ, которая гарантирует достижение требуемого уровня качества управления. При проектировании БЗ возникают трудности, связанные со сложностью динамической системы и наличием шумов в системе измерения и управления.

В данной работе рассматривается возможность подключения реального удаленного ОУ для настройки БЗ в НР в режиме реального времени на основе ОБЗ на мягких вычислениях.

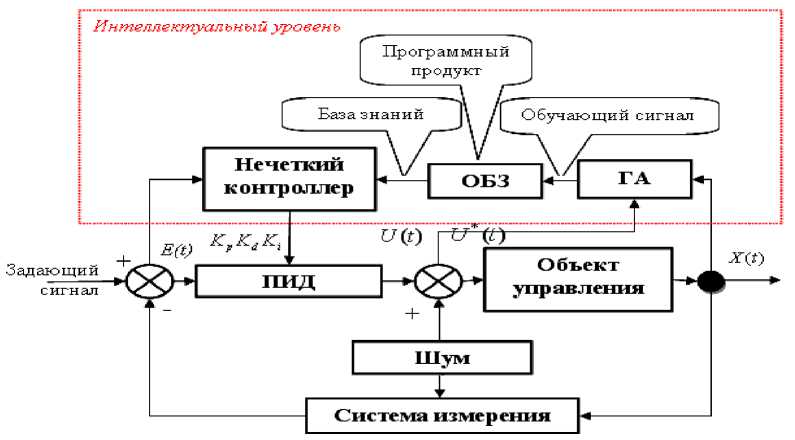
Рис. 1. Структура ИСУ с нечетким регулятором и оптимизатором баз знаний

Входом ОБЗ является обучающий сигнал (ОС), который может быть получен либо на этапе стохастического моделирования поведения ОУ (с использованием его математической модели), либо экспериментально, т.е. непосредственно из результатов измерений динамических параметров физической модели ОУ.

ОС является источником знаний и представляет собой массив данных, разделенный на входные и выходные составляющие, каждая из которых, в свою очередь, состоит из одного и более сигналов. В общем виде, каждый из составляющих сигналов является выборочной (репрезентативной) траекторией некоторого случайного процесса. При этом подразумевается, что в каждый момент времени существует некоторая корреляция между входными и выходными сигналами. Например, в случае аппроксимации некоторого управляющего сигнала, входными компонентами могут являться ошибка управления, интеграл ошибки и ее производная, а выходным компонентом – требуемое значение управляющего воздействия, либо некоторые настраиваемые параметры системы управления, например коэффициенты усиления ПИД-регулятора (рис. 2).

e	5	| edt	kp	k:	kd
		0
-O. 01	-0. 01	-0. 01	13. 38	0.48	20. 13
-0. 02	-0. 01	-0. 04	13. 38	0.48	20. 13
-0. 04	-0. 01	-0. 07	13. 38	0.48	20. 13
-0.05	-0. 01	-0. 12	13. 38	0.48	20. 13
0.25	-0. 02	7. 67	14. 20	0. 30	16. 26
0. 18	-0. 07	7. 84	14. 20	0. 30	16. 26

Рис. 2. Обучающий сигнал

На рис. 2 входными данными для НР является вектор ошибки, который состоит из ошибки управления e ( t ), интеграла ошибки управления ie = J edt и скорости изменения ошибки управления e ( t ). Выходными данными НР является вектор, состоящий из значений коэффициентов усиления k p , k _d , k _i ПИД-регулятора, значения которых применяются в формировании управляющего воздействия в виде:

u ( t ) = k p ( t ) e ( t ) + k i ( t ) J e ( t ) dT + k _d ( t ) ё( t ).                              (1)

Структурно ОБЗ состоит из взаимосвязанных генетических алгоритмов (ГА 1 , ГА 2 , ГА 3 ), оптимизирующих отдельные компоненты БЗ [1].

Базовые шаги оптимизации и структура ОБЗ представлены на рис. 3.

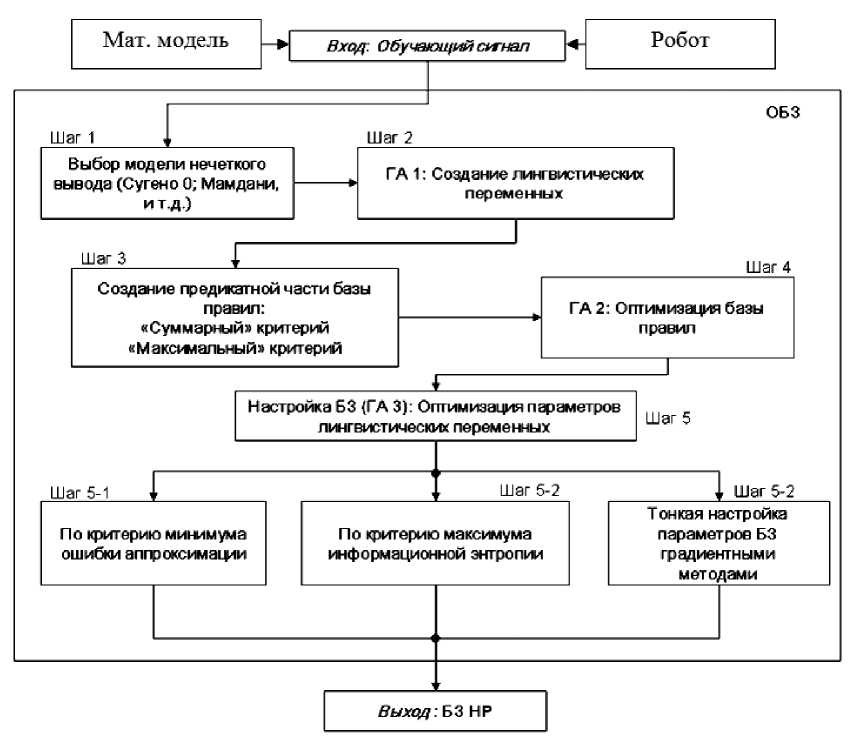
Рис. 3. Структура ОБЗ и шаги оптимизации

Рассмотрим шаги алгоритма оптимизации процесса проектирования БЗ [1]:

• -    Шаг 1: Выбор модели нечёткого вывода . Пользователь определяет тип нечёткой модели вывода (Сугено, Мамдани, и т.д.), и число входных и выходных переменных.

• -    Шаг 2: Создание лингвистических переменных . С помощью ГА 1 определяется оптимальное число ФП для каждой входной лингвистической переменной, а также выбирается оптимальная форма представления ее ФП (треугольная, Гауссовская и т.д.).

• -    Шаг 3: Создание базы правил . На данном этапе используется специальный алгоритм отбора наиболее «робастных правил» в соответствии со следующими двумя критериями:

« Суммарный » критерий : выбрать только те правила, которые удовлетворяют следующему условию:

Cai _ fr >  TL ,                                          (2)

где TL (threshold level) – заданный (вручную или выбранный автоматически) уровень активации правила, и

R L _ fr = t& ( t k ) • и R f ( t k ) = n l ^ I 1 ( x l ( t k )), ^ , _;( x 2 ( t k )),..., ^, ( X n ( t k ))] ,          (3)

k = 1

где t _k - моменты времени, k = 1,..., N , N - равно числу точек в управляющем сигнале; ^ j_k ( x k )• k = 1,..., N - ФП входных переменных, l - индекс правила в БЗ; символ «П» обозначает операцию нечеткой конъюнкции (в частности, может интерпретироваться как произведение).

« Максимальный » критерий : выбрать только те правила, которые удовлетворяют условию:

max R fr ( t ) >  TL .                                         (4)

t

• -    Шаг 4: Оптимизация базы правил . С помощью ГА 2 оптимизируются правые части правил БЗ. На данном этапе находится решение, близкое к глобальному оптимуму (минимум ошибки аппроксимации ОС). С помощью следующего шага 5 это решение может быть локально улучшено. В данной работе рассматривается возможность подключения реального удаленного ОУ для оптимизации БЗ в режиме on line.

• -    Шаг 5: Настройка базы правил . С помощью ГА 3 оптимизируются левые и правые части правил БЗ, т.е. подбираются оптимальные параметры ФП входных/выходных переменных (с точки зрения заданной функции пригодности ГА). В данном процессе оптимизации используются различные функции пригодности, выбранные пользователем (шаги 5-1, 5-2 на рис. 3). На данном этапе имеется возможность настройки БЗ с помощью традиционного метода обратного распространения ошибки (см. шаг 5-3 на рис. 3).

Результатом аппроксимации ОС является построенная БЗ для НР, включающая оптимальное конечное множество правил и оптимально сформированные параметры ФП входных и выходных переменных НР.

Таким образом, результатом проектирования является требуемый тип универсального аппроксиматора в виде НР с оптимальной структурой БЗ.

Удаленное соединение с ОБЗ

Рассмотрим модуль удаленного соединения ОБЗ и реального ОУ для оптимизации БЗ.

Удаленная оптимизация БЗ осуществляется на четвертом этапе проектирования НР (рис. 3). Реализация физической среды соединения предполагает использовать дополнительное оборудование для приема-передачи данных, например радио канал Bluetooth, WiFi или подключение по кабелю, например USB. Предполагается обмен информацией между системой управления и ОБЗ для формирования БЗ (рис. 4).

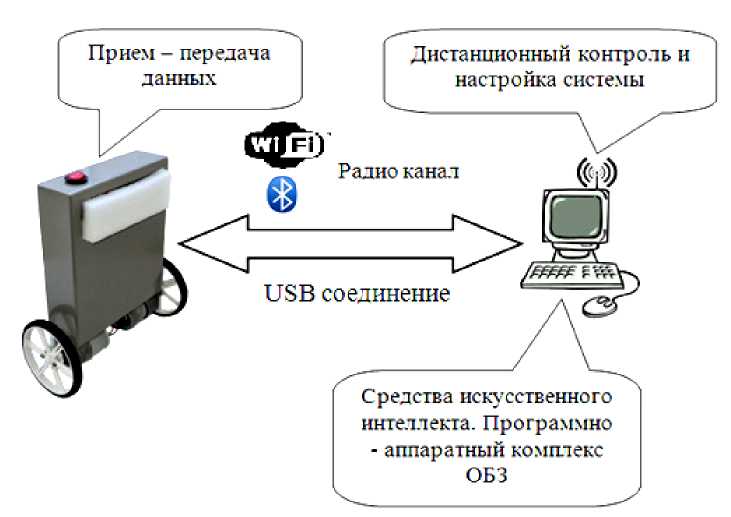
Рис. 4. Схема соединения настраиваемого устройства и ОБЗ

Рассмотрим подробнее процесс настройки функционирования подобной системы (рис. 5).

Система управления считывает показания датчиков и отправляет их на компьютер для последующей обработки. Приняв входные значения, ОБЗ оценивает предыдущее решение (БЗ НР) и осуществляет нечеткий вывод для проверки следующего решения (БЗ НР). Результат нечеткого вывода отправляется на удаленное устройство. После этого, система управления, обработав входные значения, вырабатывает управляющее воздействие.

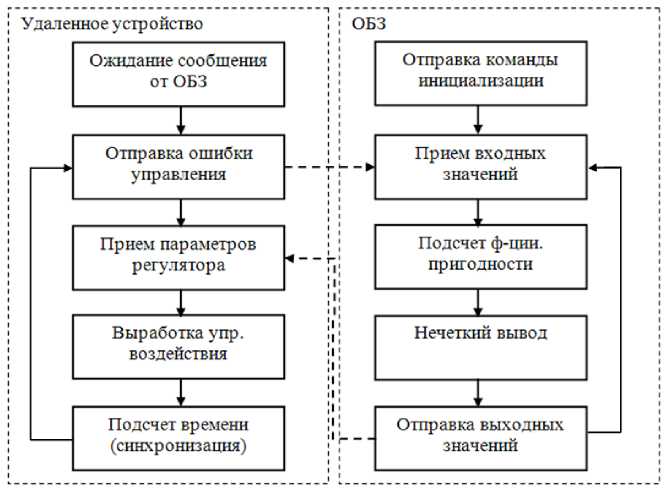
Рис. 5. Алгоритм работы удаленной настройки

Прежде чем приступить к установке соединения между оптимизатором и системой управления необходимо установить физические ограничения взаимодействующих устройств, т. е. определить максимальные и минимальные временные границы одного такта системы управления с учетом приема, передачи и обработки сообщений.

Применительно к данному макету экспериментально установлено, что максимальное время такта системы (прежде чем она потеряет управление) составляет 30мс, при использовании Bluetooth время 6

такта работы системы должно быть не менее 50 мс (прием и передача данных), что является неприемлемым. Однако, время такта системы при использовании USB кабеля 15 мс, что вполне удовлетворяет введенным ограничениям. Следует также отметить, что для настройки устройств с временным тактом системы более 50 мс, можно использовать радиоканал Bluetooth.

Синхронизация ОБЗ и системы управления осуществляется на основе удаленного устройства (робота). С этой целью разработана специальная программа (прошивка), реализующая алгоритм, представленный на рис. 5.

Профиль соединения использует последовательный порт. Скорость передачи в нашем случае составляет 115200 бит/с. В процессе функционирования, по COM-порту передаются числа с плавающей точкой в символьном виде.

Подключение к ОБЗ осуществляется через разработанный плагин. Перед установкой соединения в окне ОБЗ следует выбрать номер СОМ-порта, скорости соединения и время проверки одного решения (количество тактов системы для проверки решения) (рис. 6).

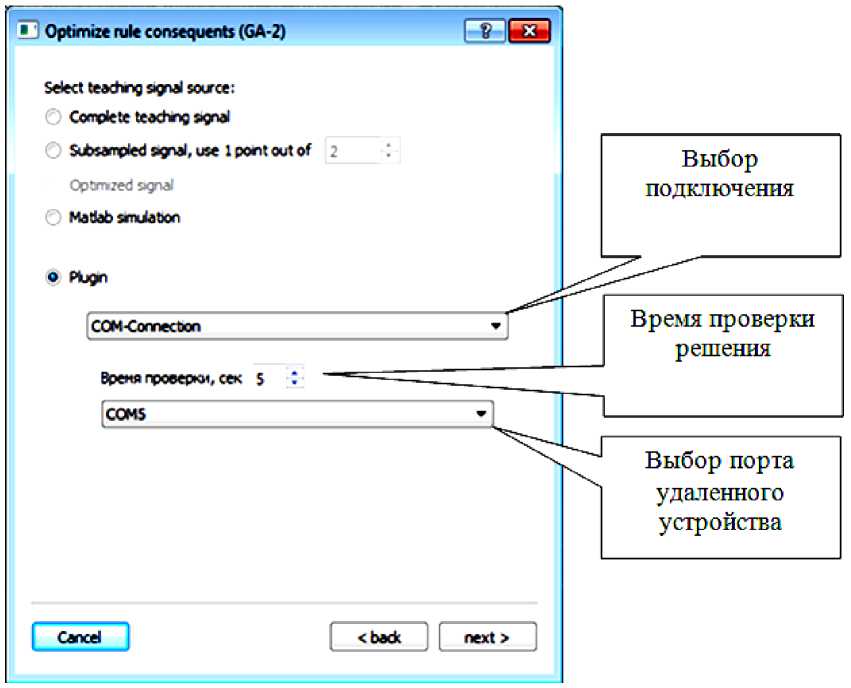
Рис. 6. Модуль удаленной настройки для ОБЗ

В данной работе рассмотрены следующие методы проектирования БЗ для НР:

• -    Метод на основе получения ОС с верифицированной модели и настройки БЗ с использованием данной модели (FC1);

• -    Метод на основе получения ОС с верифицированной модели и настройки БЗ с использованием ОУ (робота) (FC2);

• -    Метод на основе получения ОС с робота (ГА-ПИД-ОНЛАЙН регулятор) и настройки БЗ с использованием верифицированной математической модели (FC3);

• -    Метод на основе получения ОС с робота (ГА-ПИД-ОНЛАЙН регулятор) и настройки БЗ с использованием ОУ (FC4);

• -    Метод на основе получения ОС с робота, настройки на модели и дополнительной оптимиза-

• ции на макета (FC5);

• -    Метод на основе получения ОС с модели, настройки на модели и дополнительной оптимиза-

• ции на макете (FC6).

Проектирование БЗ для НР

В таком контексте возможно шесть вариантов разработки БЗ для НР (рис. 7). В данной работе ОУ является классическая задача теории управления «каретка – перевернутый маятник».

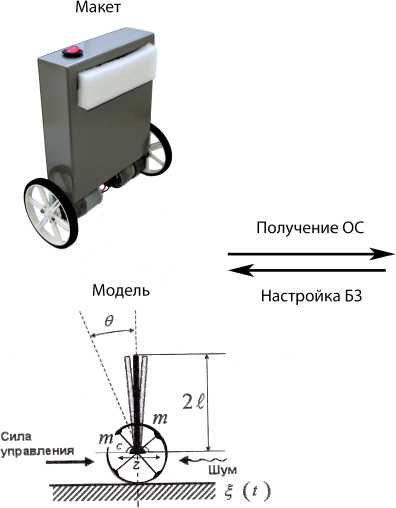
Варианты БЗ

БЗ созданая без использования математической модели

БЗ созданная на основе ОС с макета и настроенная на мат. модели

БЗ созданная на основе ОС с мат. модели и настроенная на макете

БЗ созданная без использования макета

БЗ созданная и настроенная на мат. модели и дополнительно настроенная на макете

БЗ созданная и настроенная на макте и дополнительно настроенная на мат. модели

Рис. 7. Варианты проектирования БЗ

Модель в виде одноосевой каретки с закреплённым на оси перевёрнутым вертикальным маятником, свободно вращающимся вокруг оси, представлена на рис. 8.

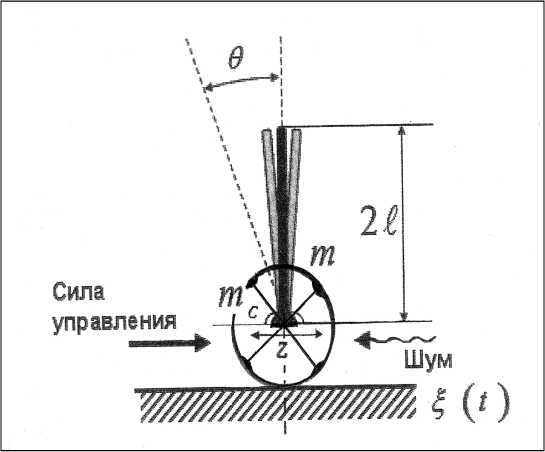
Рис. 8. Модель балансирующего макета «каретка – перевернутый маятник»

Динамика данного ОУ описывается системой дифференциальных уравнений второго порядка (5), выводимых, с учетом сил трения и упругости каретки, из баланса моментов и проекций сил на горизонтальную ось Z:

••z =

u + ^ (t)-a₁ z — a ₂ z + ml(9 sin 9 cos 9 )

g sin 9 + cos 9

тс + m f u + £(t) + a1 z + a 2 z — ml92 sin 9

— k9

••

9 =

V

тс + m

if 4

V ³

—

m cos ² 9

.

me + m J

Система позволяет вычислить управляющее воздействие на двигатели, необходимое для поддержания маятника в вертикальном положении при движении каретки:

В системе уравнений (5) z и θ – обобщенные координаты; g – ускорение свободного падения ( 9.8 m/ sec ² ), m _c – масса оси вращения (аналог массы подвижной каретки), m – масса перевернутого маятника (называемого «шест»), l – половина эффективной длины маятника, k и а ₁ коэффициенты трения о поверхность горизонтального перемещения вдоль оси z и в оси вращения θ , соответственно, а ₂ – сила упругости, препятствующая перемещению тележки, ξ ( t ) – внешний стохастический шум, а u – сила управления.

Структура компьютерной модели «каретка – перевернутый маятник», выполненная в среде моделирования MatLab/Simulink, представлена на рис. 9.

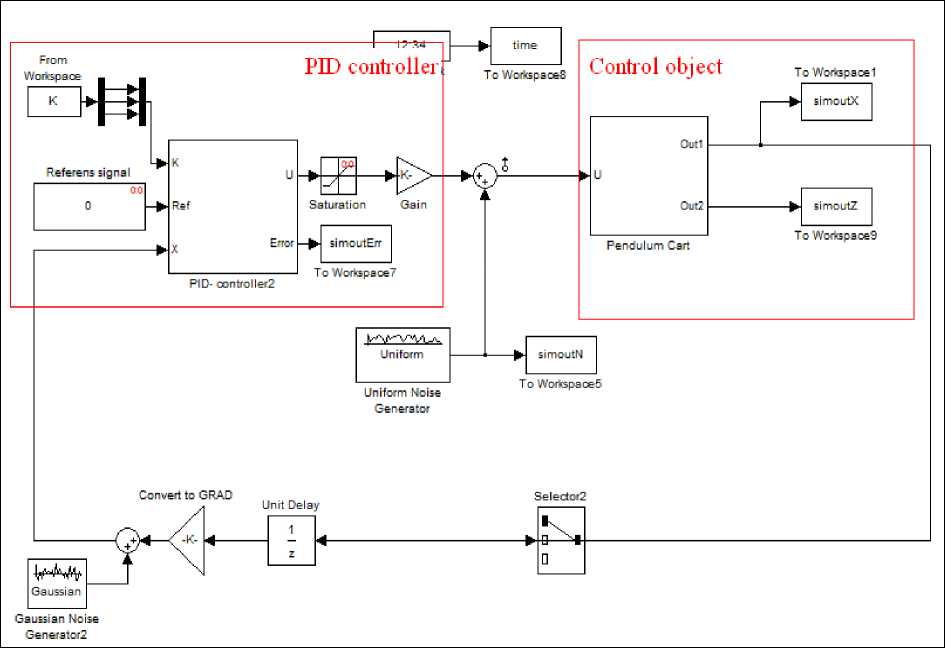
Рис. 9. Структура Matlab-модели с ПИД-регулятором

Данная модель включает в себя ПИД-регулятор, шумы в системе управления и измерения, а также блок, формирующий сигнал для регулятора. Для проведения экспериментов и получения ОС с макета использовался робот представленный на рис. 10; стенд для проведения экспериментов представлен на рис. 11.

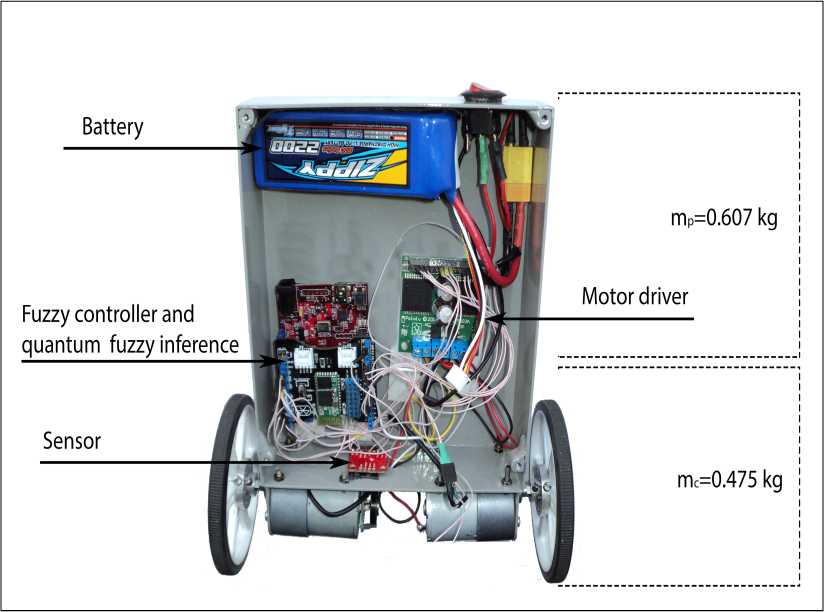
Рис. 10. Устройство робота

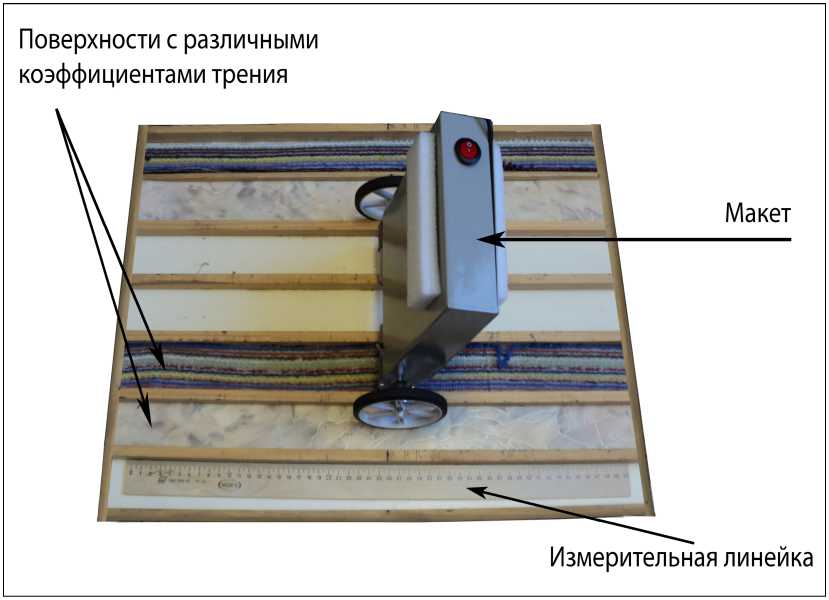
Рис. 11. Стенд для проведения экспериментов

Примечание . Стенд оборудован различными покрытиями для проведения экспериментов с макетом, в том числе в непредвиденных ситуациях управления. Измерительная линейка используется для определения величины отклонения робота по горизонтальной оси от места запуска. Также на стенде имеется возможность устанавливать определенный начальный угол для запуска макета. Для проектирования БЗ для НР на основе математической модели, была проведена верификация ОУ, методика которой рассмотрена в [2]. В дальнейшем эта модель использовалась для настройки БЗ для НР (FC1, FC2, FC5 и FC6).

Параметры верифицированной модели представлены в таблице 1.

Таблица 1. Параметры модели

	Значения параметров модели
Масса тележки	0.475 кг
Масса маятника	0.607 кг
Длина маятника (центр тяжести)	0.055 м
Коэффициент трения в креплении	112.7
Коэффициент трения колес	2350
Сила упругости	1892 мН
Шум в системе управления	Равномерный [-2.92 2.92], интенсивность 10.48
Коэффициент усиления управляющего воздействия	0.22
Шум в системе измерения	Амплитуда 0.05, Гауссовский шум, интенсивность 0.01
Задержка управляющего воздействия	0.015 с

На рис. 12 представлена часть ОС, полученного с данной модели.

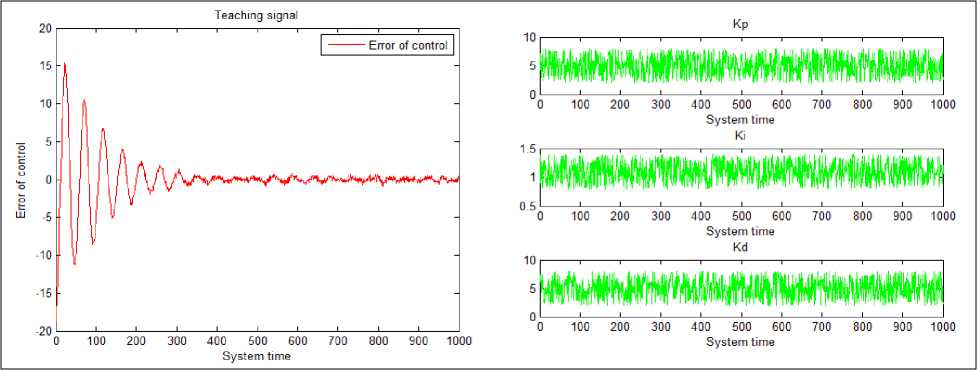
Рис. 12. Обучающий сигнал с модели.

Слева – ошибка управления, справа – коэффициенты усиления ПИД-регулятора

В дальнейшем этот сигнал используется для создания FC1, FC3 и FC5. Для получения ОС с макета используется ГА-ПИД регулятор в режиме on line [2].

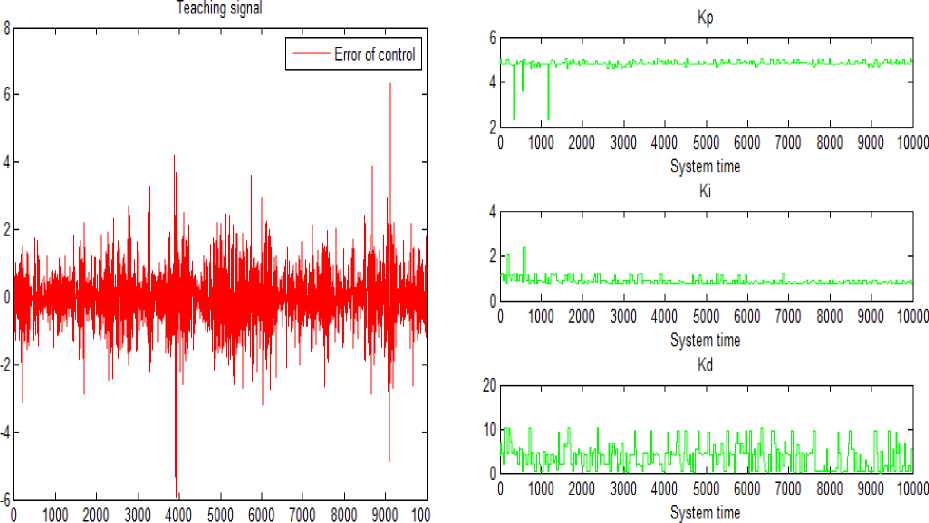
Часть ОС, полученного с макета, представлена на рис. 13.

Error of control

System time

Рис. 13. Обучающий сигнал с макета.

Слева - ошибка управления, справа - коэффициенты усиления ГА-ПИД-регулятора.

На этапе создания БЗ (рис.3, шаг 2) полученные ОС используются для формирования лингвистических переменных для входных значений.

Результаты первого этапа проектирования представлены на рис. 14 и 15.

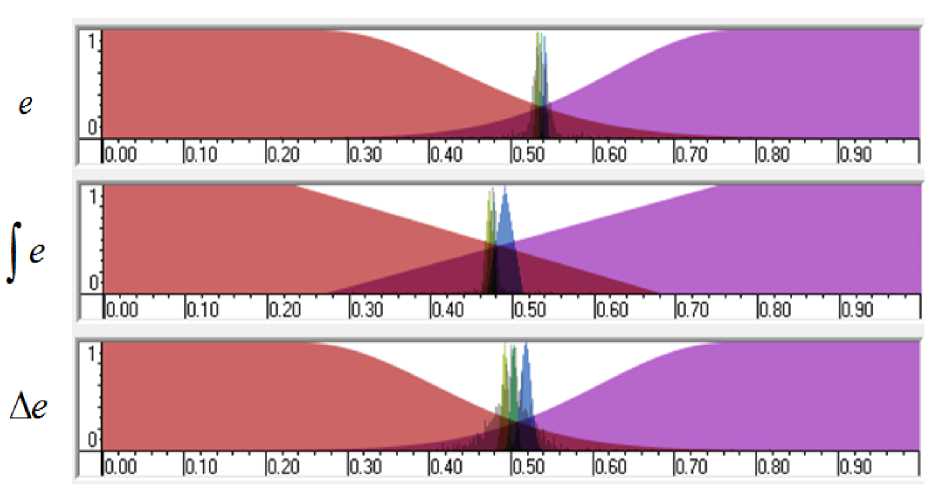
Рис. 14. Функции принадлежности входных переменных (FC1, FC2 и FC5) на основе ОС с модели

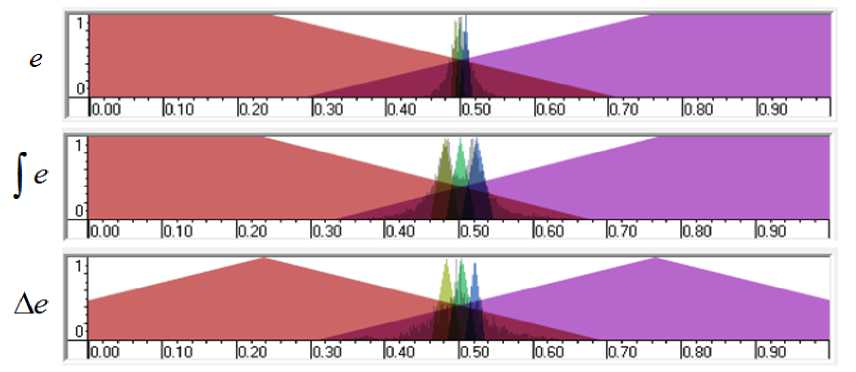
Рис. 15. Функции принадлежности входных переменных (FC3, FC4 и FC6) на основе ОС с макета

В данной работе количество нечетких множеств в каждой лингвистической переменной было ограничено до 5.

На следующем этапе проектирования БЗ для НР осуществляется формирование и оптимизация количества правил НР (рис. 3, шаг 3). Результат данного этапа представлен на рис. 16. Выходные значения на данном этапе равны 0, т.к. их настройка производится на следующем этапе проектирования НР.

В данной работе рассматриваются полные БЗ, состоящие из 125 правил. Такой подход используется для более точного сравнения источников ОС и методов оптимизации.

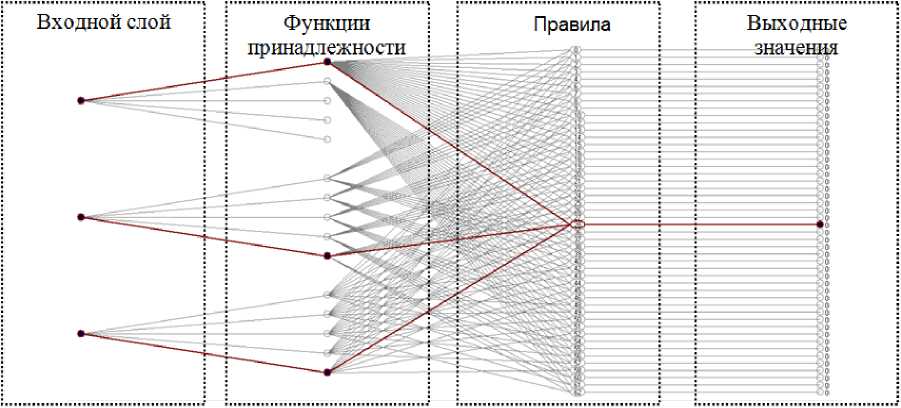
Рис. 16. Нейронная сеть нечеткого регулятора

На следующем этапе проектирования настраиваются выходные значения НР (рис.3, шаг 4). В данной работе рассматривается метод оптимизации БЗ с использованием математической модели и метод оптимизации БЗ с использованием подключения удаленного устройства.

В Таблице 2 проводится сравнение полученных НР по методам получения ОС и методам настройки.

Таблица 2. Сравнение НР

	Источник ОС	Метод настройки	Количество правил
FC1	Мат. модель	Мат. моделирование	125
FC2	Макет (ГА-ПИД)	Мат. моделирование	125
FC3	Мат. модель	Удаленное соединение	125
FC4	Макет (ГА-ПИД)	Удаленное соединение	125
FC5	Математическая (мат) модель	Мат. моделирование и дополнительная настройка с использованием удаленного соединения	125
FC6	Макет (ГА-ПИД)	Удаленное соединение и дополнительная настройка на мат. модели	125

Моделирование и эксперимент

Эксперимент и моделирование проводились в двух ситуациях управления. Первая ситуация (С1) является типичной для системы управления (начальный угол равный -1о и ускорение равное 1м/c2. Цель управления поддерживать маятник в равновесии (угол отклонения 0о). Следует отметить, что оптимизация БЗ проходила в типовой ситуации управления. Вторая ситуация является непредвиденной (С2). Начальный угол и ускорение в С2 равны 5о и 1м/c2 соответственно. Такая ситуация характеризует возмущение, вызванное внешним воздействием на ОУ. Рассмотрим результаты моделирования в типовой ситуации управления (рис. 17-20).

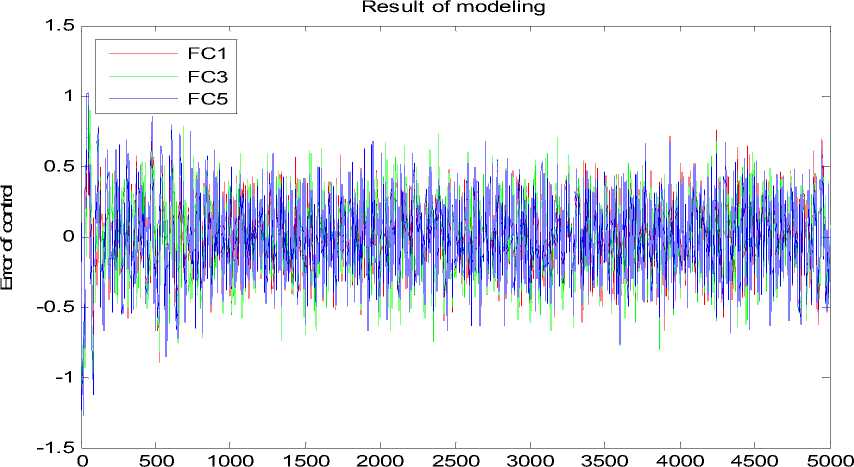
System time

Рис. 17. Ошибка управления. Типовая ситуация управления. Моделирование НР на основе ОС с математической модели

Error of control

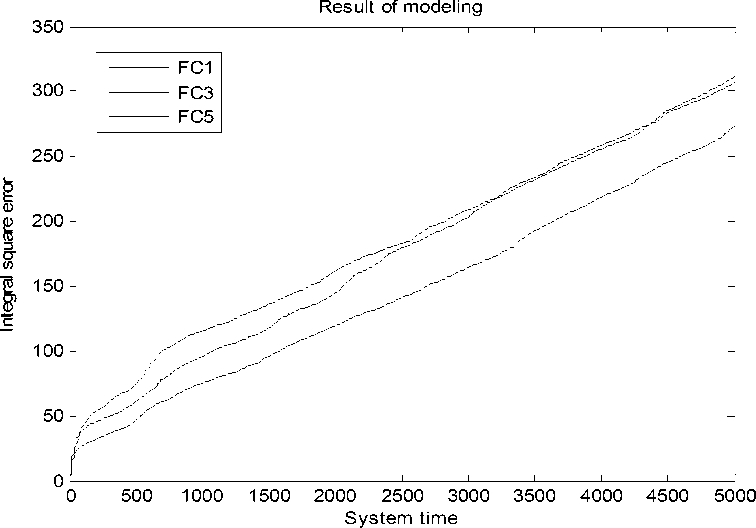
Рис. 18. Интеграл квадратичной ошибки. Типовая ситуация управления. Моделирование НР на основе ОС с математической модели

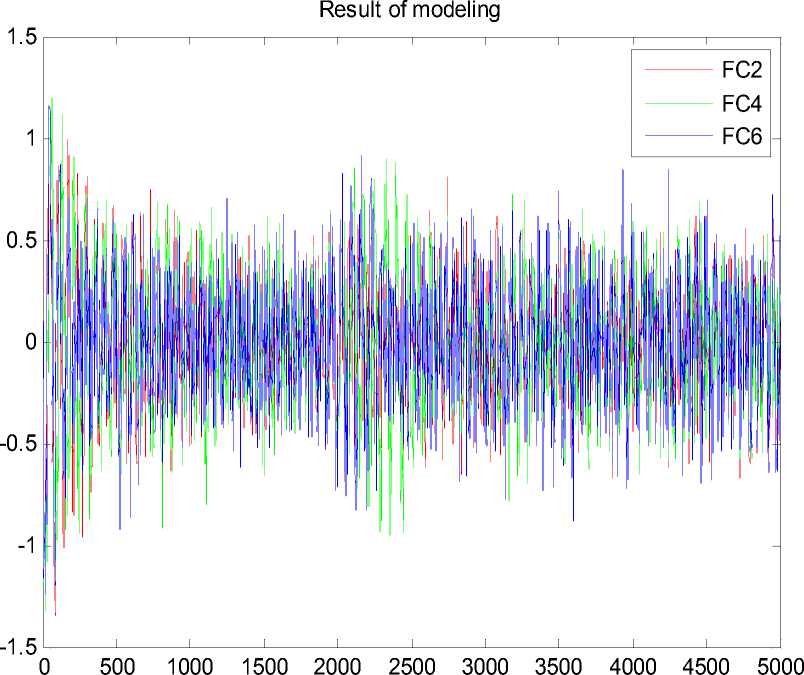
System time

Рис. 19. Ошибка управления. Типовая ситуация управления. Моделирование. НР на основе ОС с макета

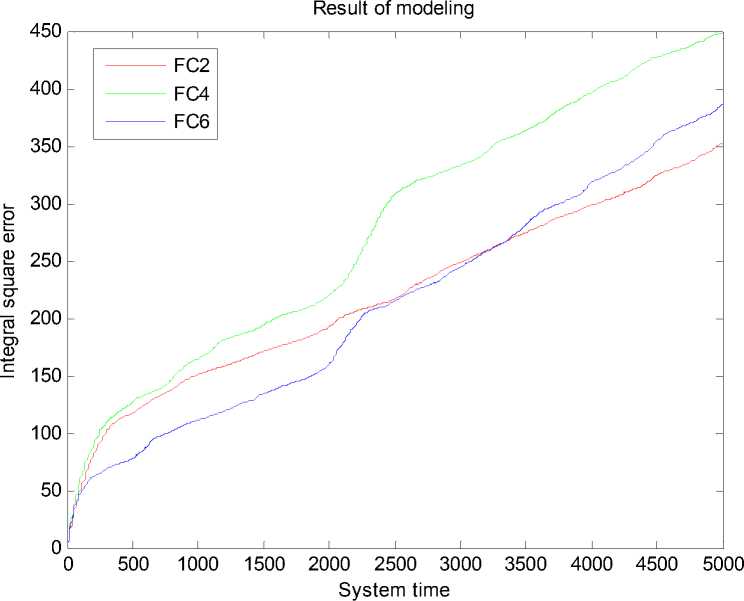
Рис. 20. Интеграл квадратичной ошибки. Типовая ситуация управления. Моделирование НР на основе ОС с макета

Рассмотрим результаты эксперимента в типовой ситуации управления (рис. 21-24).

Error of control

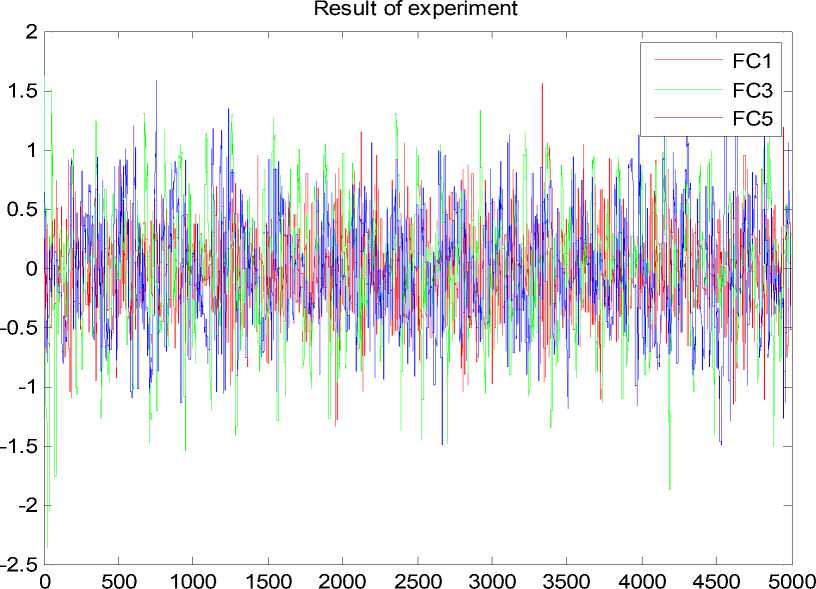
System time

Рис. 21. Ошибка управления. Типовая ситуация управления. Эксперимент. НР на основе ОС с математической модели

Error of control                                                                    Integral square error

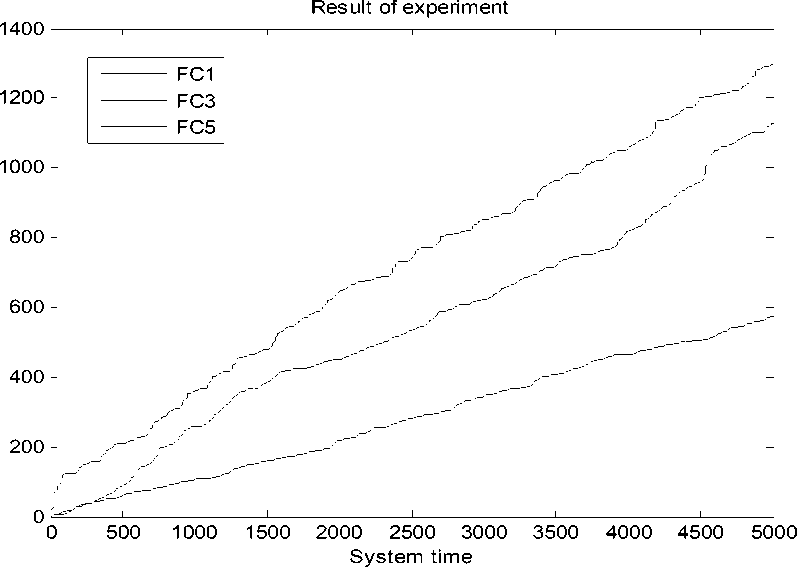
Рис. 22. Интеграл квадратичной ошибки. Типовая ситуация управления. Эксперимент. НР на основе ОС с математической модели

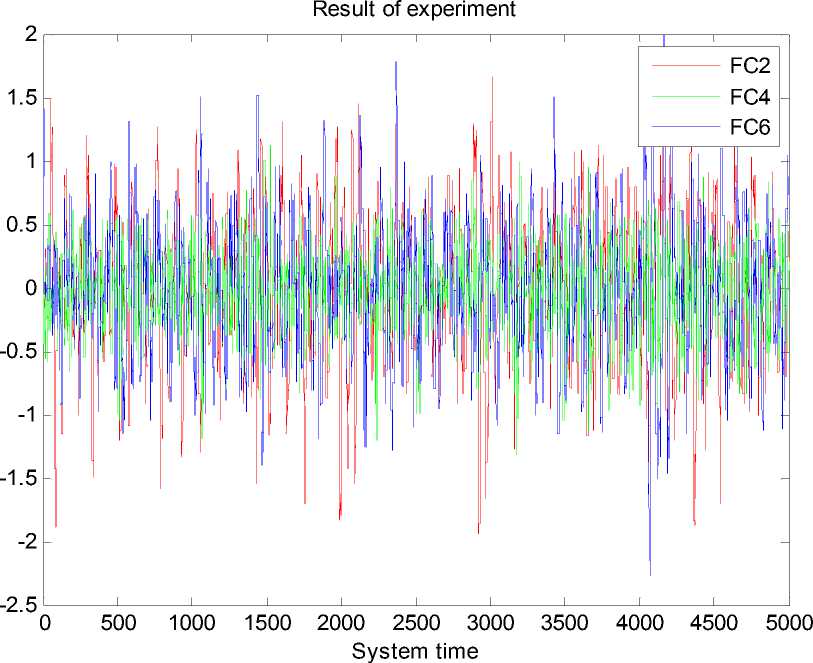
Рис. 23. Ошибка управления. Типовая ситуация управления. Эксперимент. НР на основе ОС с макета

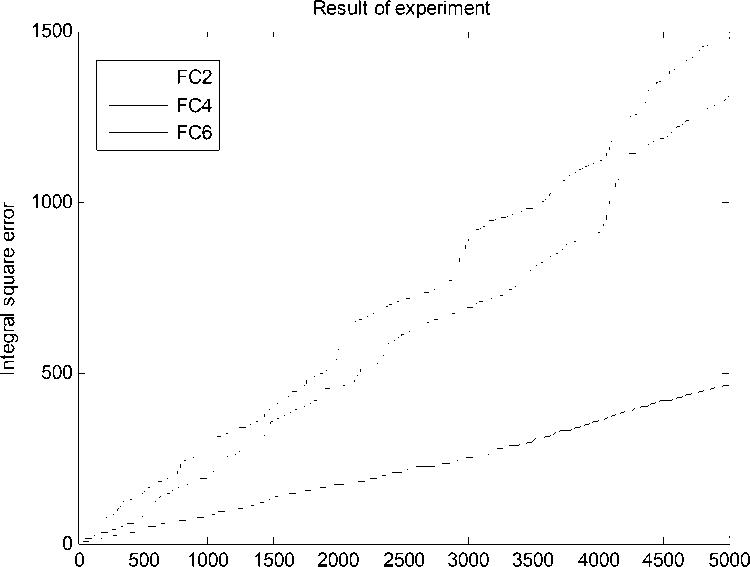
System time

Рис. 24. Интеграл квадратичной ошибки. Типовая ситуация управления. Эксперимент. НР на основе ОС с макета

На рис. 25 представлено сравнение интегралов квадратичной ошибки для всех рассматриваемы регуляторов в типовой ситуации управления.

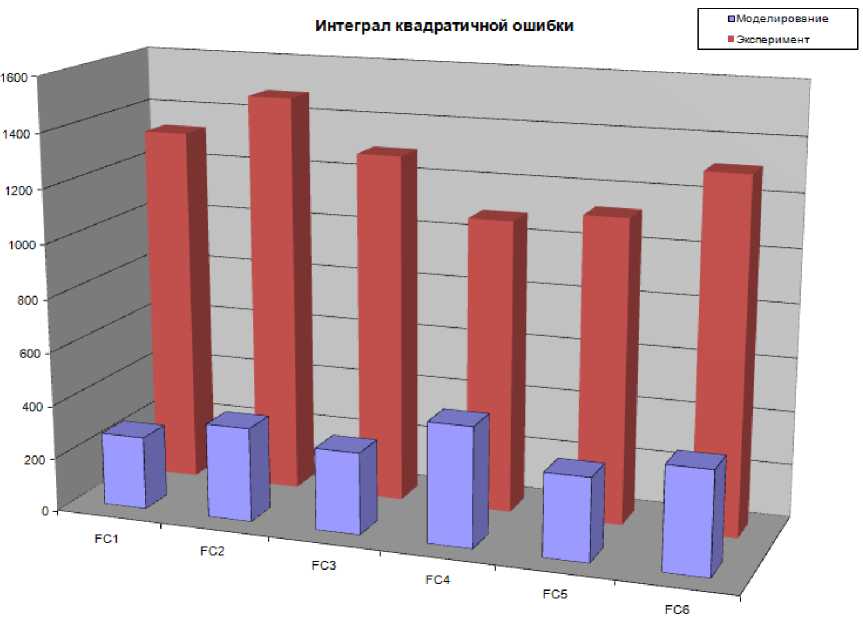
Рис. 25. Интеграл квадратичной ошибки. Типовая ситуация управления

Меньший по высоте уровень интеграла квадратичной ошибки на рис. 25 свидетельствует о лучшей работе регулятора. Из результатов на рис. 25 видно, что в эксперименте FC4 справился с задачей управления в типовой ситуации лучше других регуляторов. Результаты моделирования показывают, что FC1 разработанный и оптимизированный с использованием математической модели, справляется с задачей управления лучше остальных регуляторов. Это объясняется тем, что дня настройки FC1 используется математическая модель, а для настройки FC4 реальный ОУ (макет) с неопределенными параметрами. Рассмотрим результаты моделирования и эксперимента в непредвиденной ситуации управления (рис 26-33).

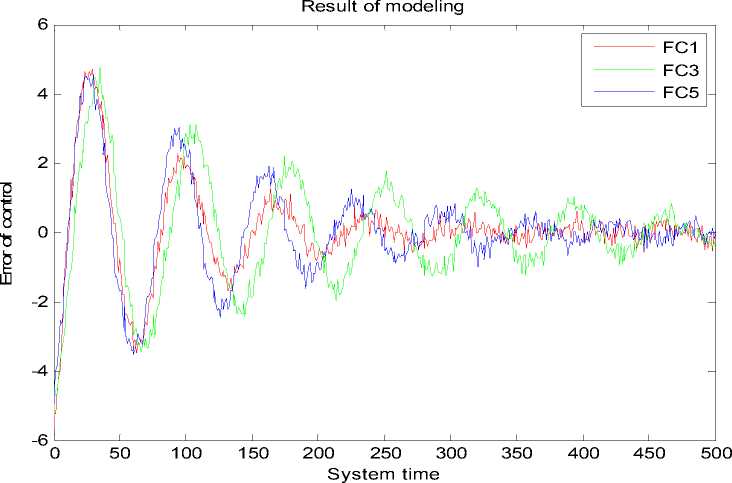
Рис. 26. Ошибка управления. Непредвиденная ситуация управления. Моделирование. НР на основе ОС с математической модели

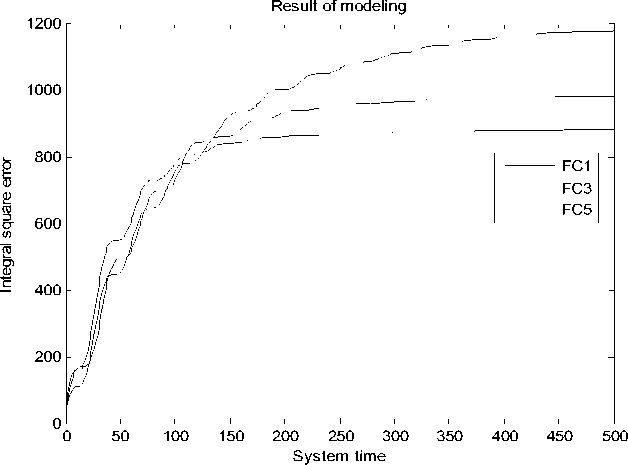
Рис. 27. Интеграл квадратичной ошибки. Непредвиденная ситуация управления. Моделирование. НР на основе ОС с математической модели

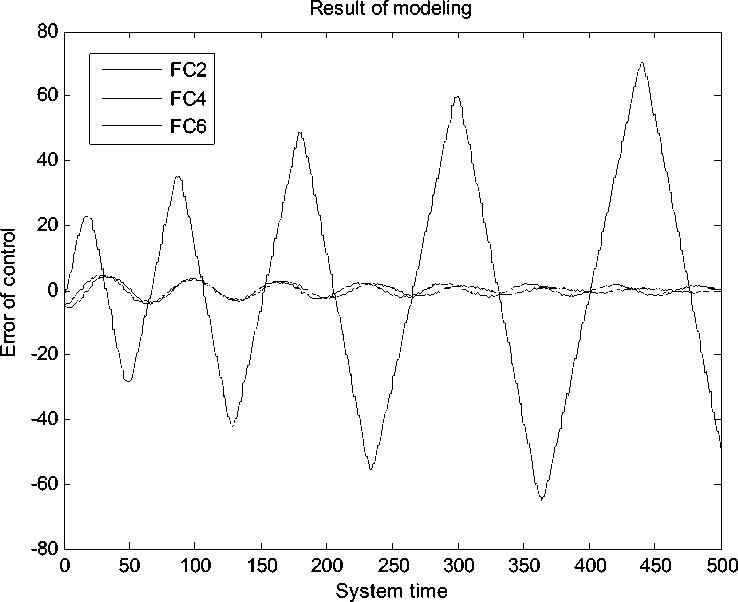
Рис. 28. Ошибка управления. Непредвиденная ситуация управления. Моделирование. НР на основе ОС с макета

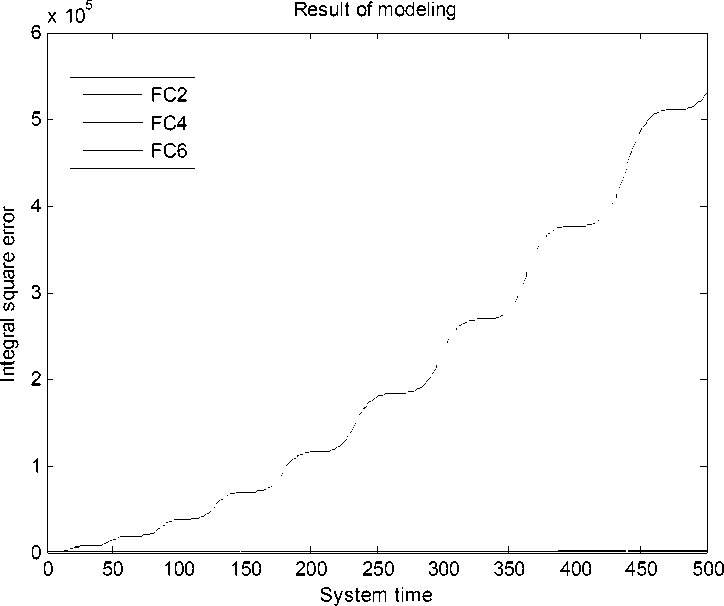
Рис. 29. Интеграл квадратичной ошибки. Непредвиденная ситуация управления. Моделирование. НР на основе ОС с макета

о

"с 2

о о

о

I0

ш

-2

-4

0     50    100   150   200   250   300   350   400   450   500

System time

Рис. 30. Ошибка управления. Непредвиденная ситуация управления. Эксперимент. НР на основе ОС с математической модели

-6

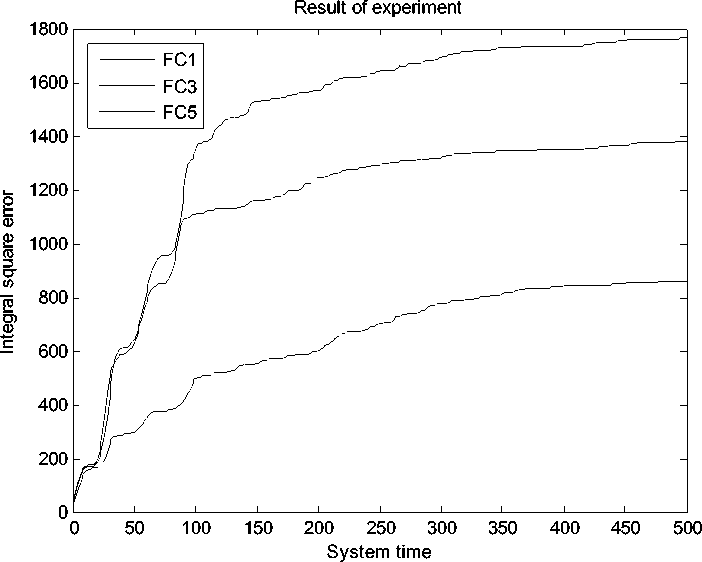
Рис. 31. Интеграл квадратичной ошибки. Непредвиденная ситуация управления. Эксперимент. НР на основе ОС с математической модели

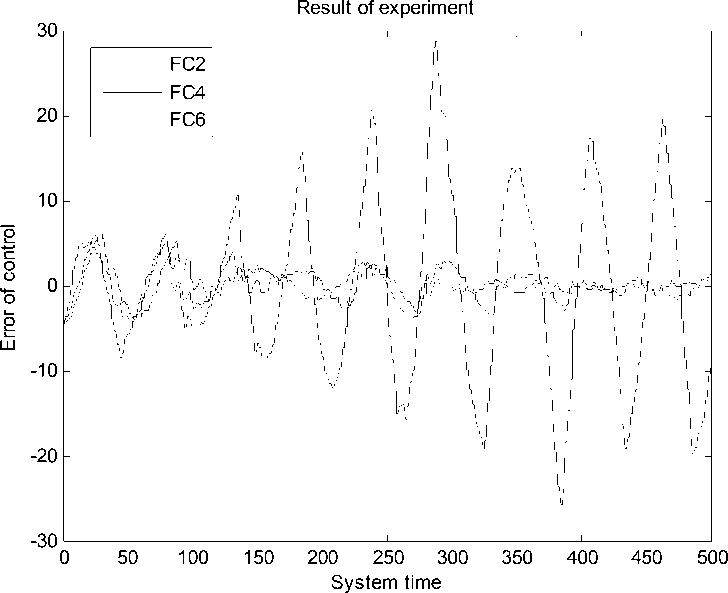
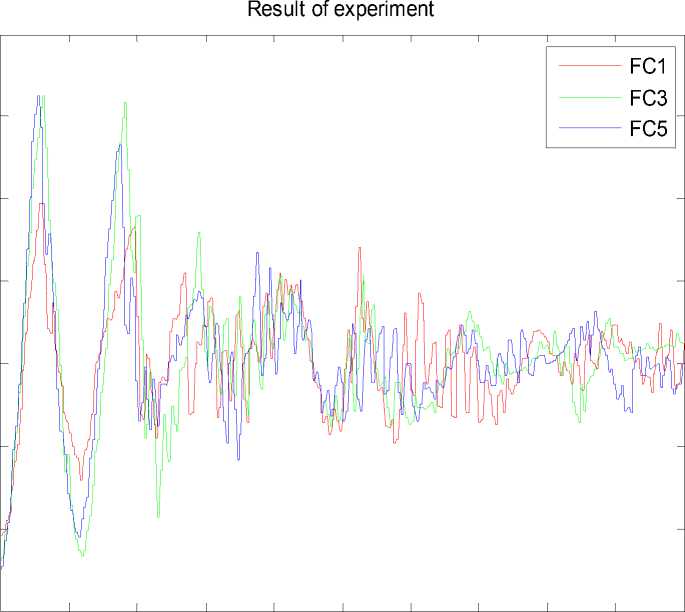
Рис. 32. Ошибка управления. Непредвиденная ситуация управления. Эксперимент. НР на основе ОС с макета

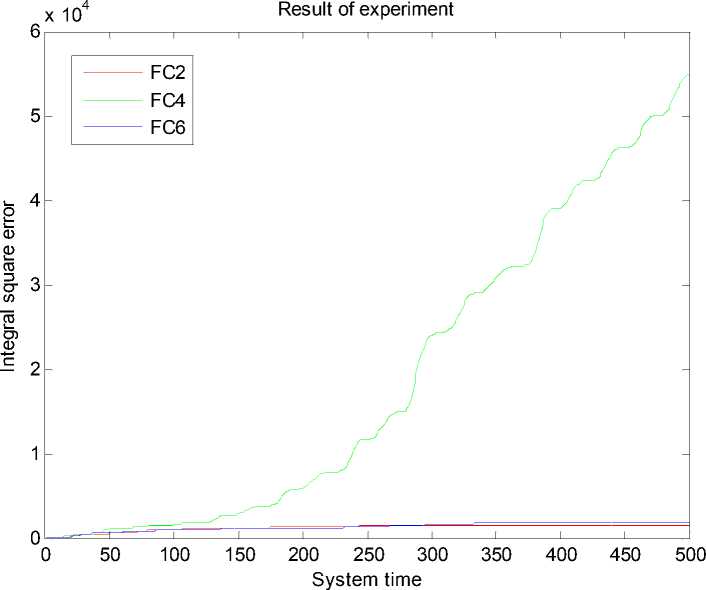
Рис. 33. Интеграл квадратичной ошибки. Непредвиденная ситуация управления. Эксперимент. НР на основе ОС с макета

На рис. 34 представлено сравнение интегралов квадратичной ошибки всех НР.

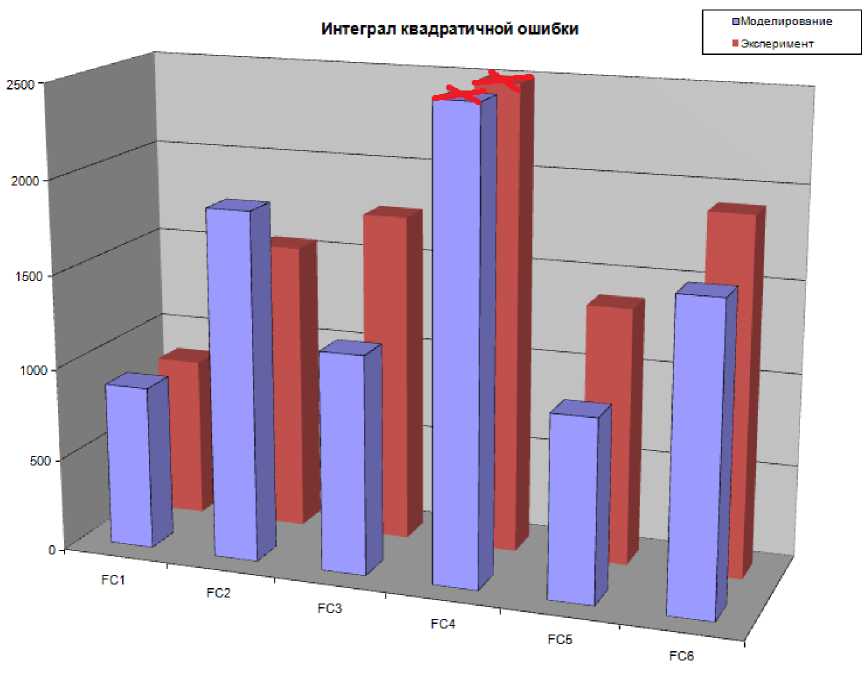
Рис. 34. Интеграл квадратичной ошибки. Непредвиденная ситуация управления

Результаты моделирования и эксперимента показывают, что FC4, разработанный без использования математической модели, не обладает достаточной робастностью.

FC1, разработанный только на основе математической модели ОУ, обладает лучшей робастностью. Следует отметить, что и FC5, разработанный на основе совместного использования математической модели и дистанционной настройки, обладает достаточно хорошим качеством управления. Этот регулятор FC5 в типовой и непредвиденной ситуации справляется с задачей управления на достаточно высоком уровне.

Анализ результатов моделирования и экспериментов

Для оценки качества процесса управления используются показатели переходного процесса (рис. 35). К таким показателям относятся: сложность управления, устойчивость, величина перерегулирования.

Перерегулирование характеризует колебательное свойство переходного процесса и рассчитывается согласно выражению:

O i = i - O-; O m ( const .) ^ O i ;                                     (6)

m

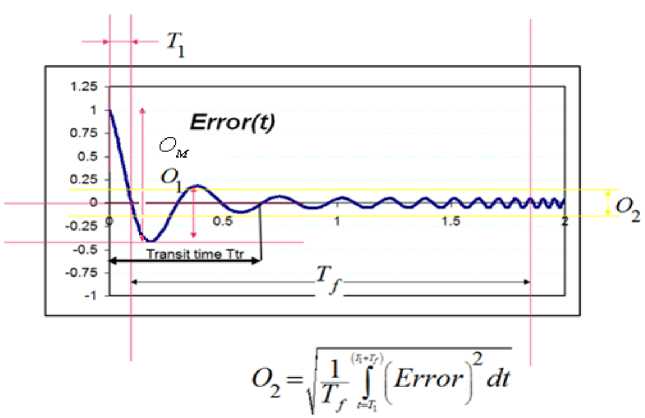
Рис. 35. Показатели качества управления

На рис. 36 представлена диаграмма уровня перерегулирования систем управления.

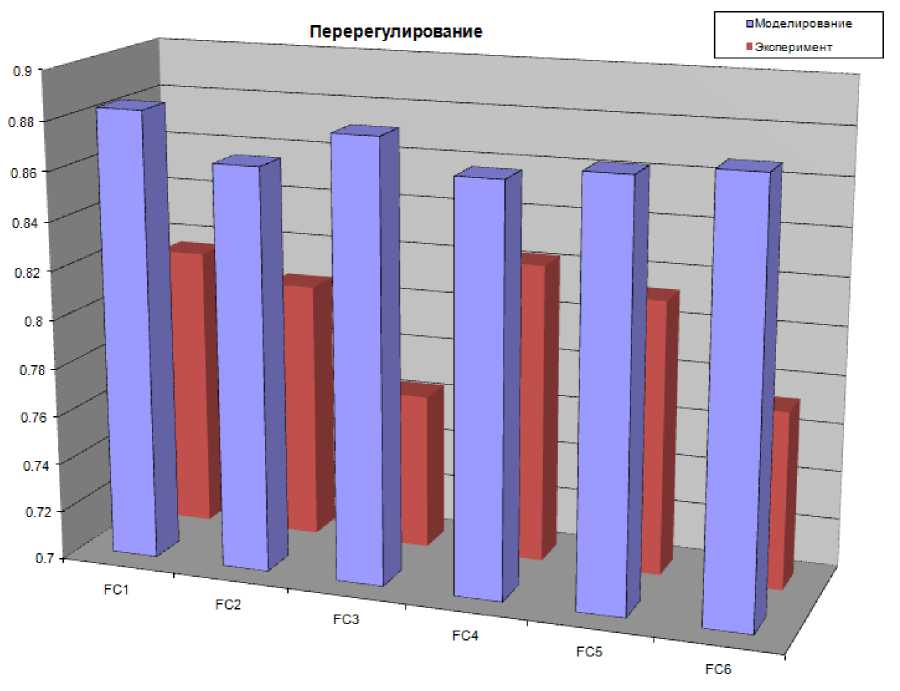
Рис. 36. Перерегулирование систем управления в типовой ситуации. Моделирование и эксперимент

При моделировании НР разработанный на основе верифицированной математической модели, имеет более высокий показатель перерегулирования, что характеризует работу такого регулятора как более эффективную. В эксперименте более эффективное управление с точки зрения перерегулирования демонстрирует FC4, оптимизированный на основе удаленного соединения.

Худшими по качеству управления регуляторами с точки зрения перерегулирования являются FC3 и FC2 в эксперименте и моделировании соответственно.

Устойчивость переходного процесса (рис. 37) рассчитывается как:

O y = ¹ - O^; O m ( const .) ^ O 2 ^.

m

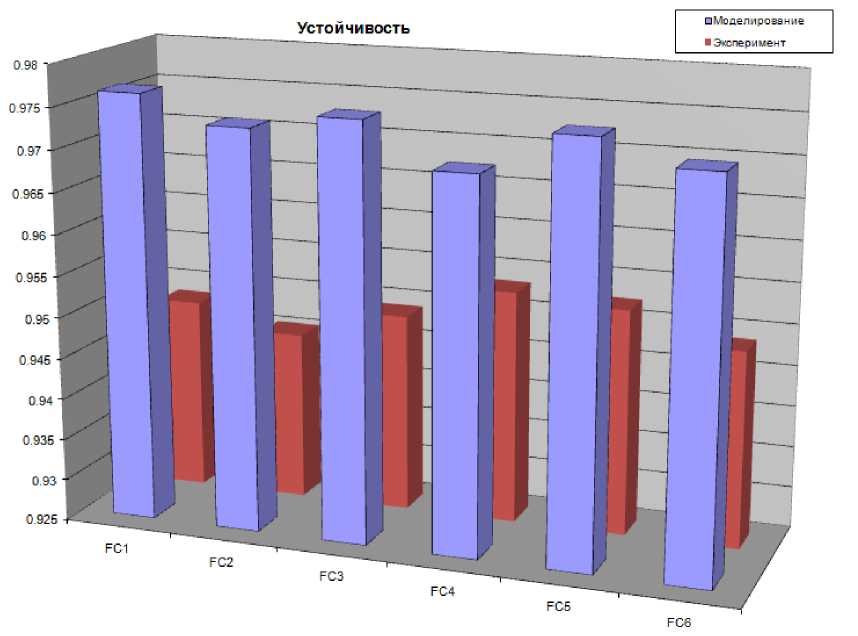
Рис. 37. Устойчивость систем управления в типовой ситуации.

Моделирование и эксперимент

Более высокий уровень устойчивости свидетельствует о более лучшем уровне управления. При моделировании в типовой ситуации управления более устойчивым регулятором оказался FC1, однако FC4 с точки зрения устойчивости оказался худшим.

Однако результаты эксперимента показали, что самым устойчивым регулятором оказался FC4, а самым неустойчивым – FC2.

Качество управления характеризует способность системы управления эффективно расходовать энергетический и технический ресурс системы. В случаи реализации сложного управления, износ оборудования и затраты энергии будут велики.

Сложность управления (рис. 38) рассчитывается в виде:

P = 1 -

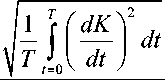
A

; A = ( const ).

к                7

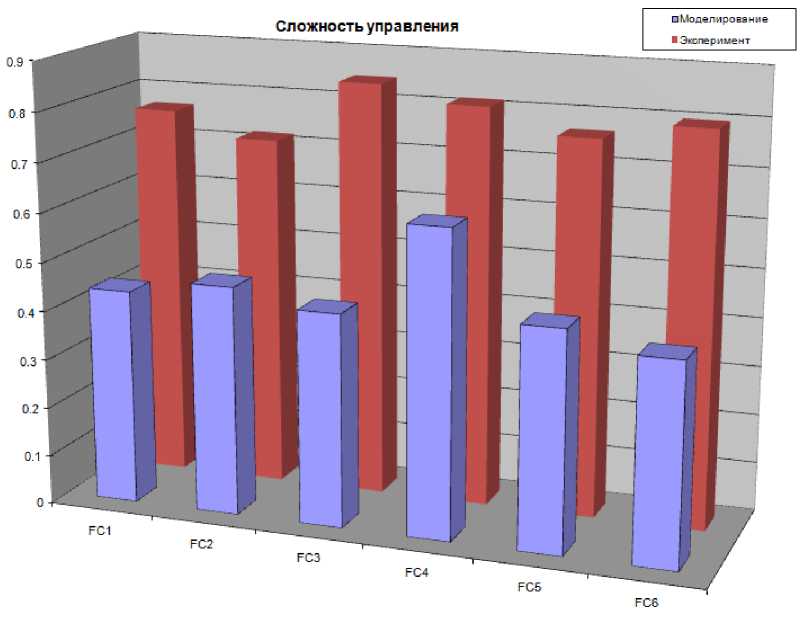
Рис. 38. Сложность управления в типовой ситуации. Моделирование и эксперимент

В типовой ситуации управления FC4 обладает более простым и, следовательно, эффективным управлением.

Анализ результатов моделирования в типовой ситуации показывает, что НР, настроенные с использованием математической модели обладают более высоким качеством управления. Однако, анализ результатов эксперимента в типовой ситуации показывает, что этим качеством обладают НР, настроенные с использованием дистанционного соединения.

Проведем анализ качества управления в непредвиденной ситуации управления (рис. 39-41).

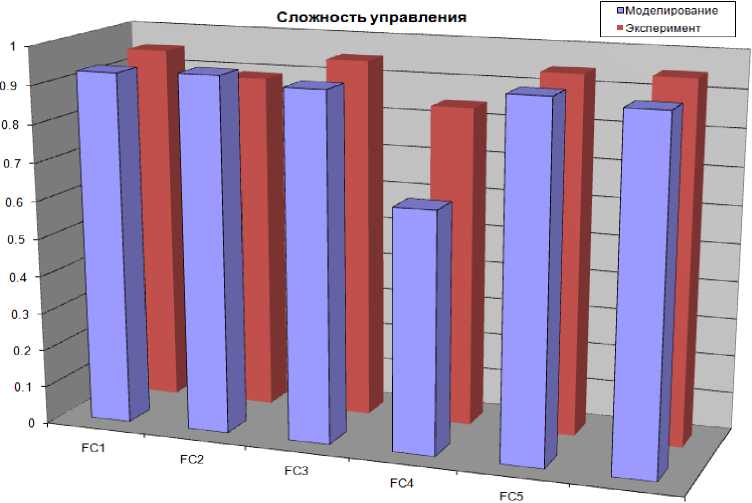
Результаты моделирования и эксперимента показали, что в непредвиденной ситуации управления FC4 не обладает достаточной устойчивостью и имеет низкую оценку качества с точки зрения перерегулирования. Эффективным управлением с точки зрения сложности управления обладают регуляторы FC1, FC3, FC5 и FC6.

В непредвиденной ситуации результаты моделирования и эксперимента показывают, что высоким уровнем робастности обладают НР, разработанные с использованием математической модели.

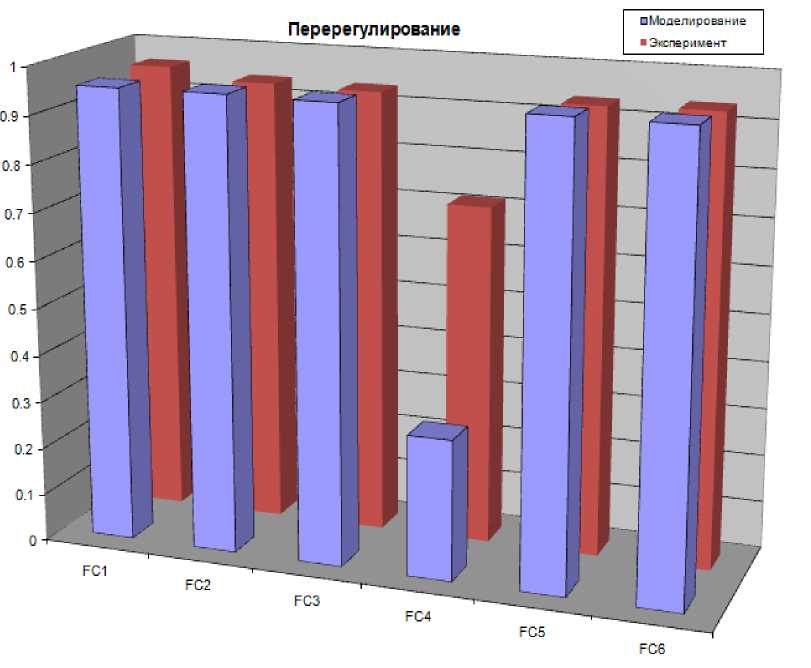
Рис. 39. Перерегулирование систем управления в непредвиденной ситуации. Моделирование и эксперимент

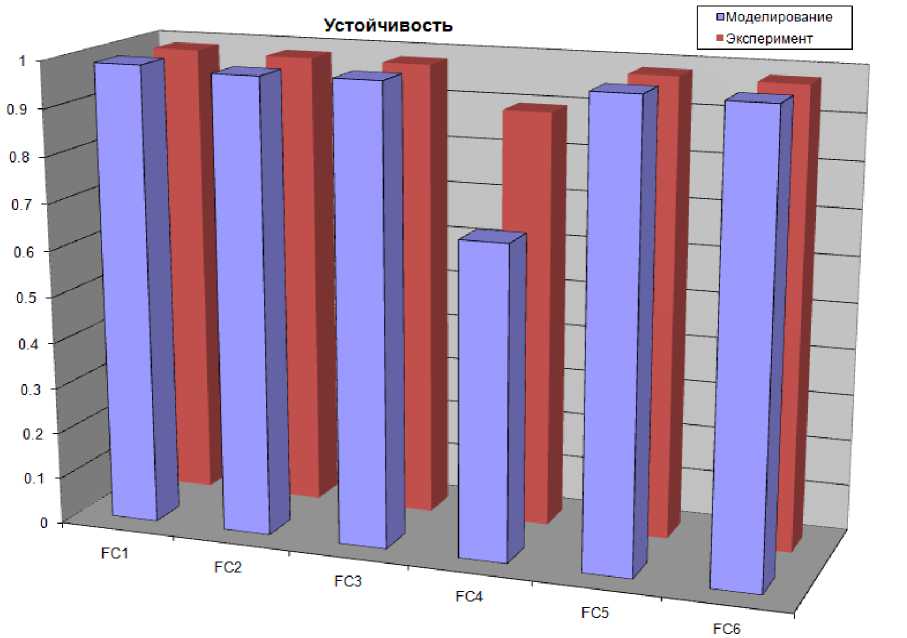
Рис. 40. Устойчивость систем управления в непредвиденной ситуации. Моделирование и эксперимент

FC6

Рис. 41. Сложность управления в непредвиденной ситуации.

Моделирование и эксперимент

Для сравнения качества управления используем сумму показателей качества с равными весами в обеих ситуациях управления и рассчитаем общее качество управления по формуле (рис. 42):

Общее качество = ^ w 1 • O 1 i + w ₂ • O 2 i + w ₃ • P i ,                       (9)

i где w1 = w2 = w3 = 0.16.

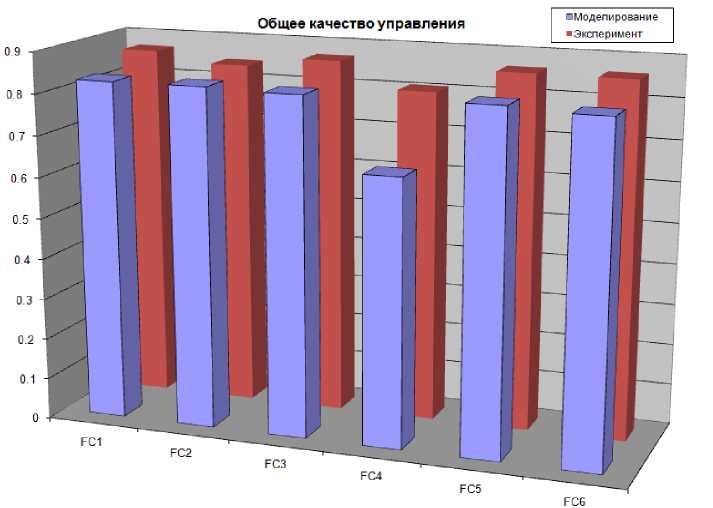
Рис. 42. Общее качество управления в двух ситуациях управления

Из рис. 42 видно, что абсолютно хорошо справляются с задачей управления в типовой и непредвиденной ситуации управления четыре регулятора:

• -    FC1 (ОС с математической модели и настройка с использованием математической модели),

• -    FC3 (ОС с математической модели и настройка с использованием дистанционного соединения с ОУ);

• -    FC5 (ОС с математической модели, настройка с использованием математической модели и дополнительная настройка с использованием дистанционного соединения);

• -    FC6 (ОС с макета, настройка с использованием дистанционного соединения и дополнительная настройка на математической модели).

Выводы

Оптимизация БЗ с использованием дистанционного соединения с ОУ непосредственно напрямую с ОБЗ даёт ряд преимуществ:

• -    позволяет не строить математическую модель и при этом получать знания об ОУ для построения БЗ;

• -    для проектирования ИСУ в ОБЗ достаточно снять информативные показатели и параметры поведения ОУ;

• -    дистанционное соединение позволяет оптимизировать БЗ в определенных (типовых) условиях функционирования, тем самым создавать множество БЗ с высоким качеством управления для различных ситуаций управления.

Результаты моделирования и экспериментов показывают, что для проектирования качественной и робастной ИСУ недостаточно использовать только математическую модель или реальный ОУ. Только совместное использование этих информационных ресурсов дает синергетический эффект повышения качества проектируемых ИСУ.