Технология оптимального проектирования сложноструктурированных систем с распределёнными параметрами: программные стратегии принятия решений
Автор: Рапопорт Э.Я., Плешивцева Ю.Э.
Журнал: Онтология проектирования @ontology-of-designing
Рубрика: Методы и технологии принятия решений
Статья в выпуске: 2 (24) т.7, 2017 года.
Бесплатный доступ
В статье приводятся постановки и предлагаемая технология решения широкого круга задач совместной оптимизации по комплексным критериям эффективности проектных разработок и режимов функционирования сложноструктурированных бесконечномерных детерминированных и не полностью определённых систем с распределёнными параметрами применительно к их описанию операторными уравнениями достаточно общего вида с соответствующими начальными и краевыми условиями. В качестве базовой рассматривается детерминированная задача оптимального проектирования программных управлений режимами функционирования распределённой системы с полным объёмом информации о характеристиках объекта. Предлагаемый метод её решения последовательно распространяется на задачи оптимизации проектных разработок в условиях априори фиксируемых внешних воздействий на объект; на комплексную проблему совместной оптимизации и далее на типичные ситуации оптимального проектирования распределённой системы в условиях интервальной неопределённости её параметрических характеристик и внешних возмущений. Развиваемый подход использует предварительную процедуру параметризации искомых решений, опирающуюся на известные аналитические условия оптимальности; последующую операцию точной редукции к специальным задачам математического программирования; альтернансные свойства их экстремалей, подобные известным результатам теории нелинейных чебышёвских приближений, и фундаментальные закономерности предметной области. Приводится представляющий самостоятельный интерес пример применения полученных результатов общего характера к задаче оптимального проектирования промышленного объекта технологической теплофизики производственного назначения. Предлагаемая интерпретация проблемы оптимального проектирования систем с распределёнными параметрами в виде комплексной задачи совместного поиска соответствующих компонентов векторных пространственно-временных управляющих воздействий и обобщенная на достаточно широкий круг подобных задач технология разработки на этой основе программных стратегий принятия решений являются новыми.
Система с распределёнными параметрами, оптимальное проектирование, полубесконечная оптимизация, альтернансный метод
Короткий адрес: https://sciup.org/170178750
IDR: 170178750 | УДК: 62-40 | DOI: 10.18287/2223-9537-2017-7-2-172-190
Текст научной статьи Технология оптимального проектирования сложноструктурированных систем с распределёнными параметрами: программные стратегии принятия решений
Новые возможности решения актуальной проблемы оптимального проектирования технических систем управления появляются при её трактовке в соответствии с современными требованиями системного подхода в качестве задачи совместного поиска проектных разработок и режимов последующего функционирования объекта, обеспечивающих в совокупно- сти достижение экстремальной величины априори выбираемого комплексного техникоэкономического критерия оптимальности. Трудности решения подобной задачи существенно увеличиваются с возрастанием сложности структуры объекта и порядка динамических моделей его описания, приобретая принципиальный характер применительно к бесконечномерным системам с распределёнными параметрами (СРП) [1-8].
В целом ряде наиболее характерных для прикладных задач ситуаций подобная совокупная проблема поиска проектных решений и способов организации динамических режимов функционирования СРП может быть сведена к поиску понимаемых в обобщённом смысле соответствующих оптимальных векторных управляющих воздействий (УВ). Их составляющие, относящиеся к проектным разработкам, интерпретируются в своих основных аспектах в роли пространственно-распределённых «статических» УВ, а компоненты, определяющие поведение объекта в динамических режимах – как традиционные, изменяющиеся во временной или пространственно-временной области управления.
Известные условия оптимальности во многих случаях позволяют заведомо установить для типовых моделей СРП базовую программную структуру подобных УВ в форме их явной зависимости от временного и пространственного аргументов с точностью до числа и конкретных значений компонентов конечномерного вектора некоторой определённым образом упорядочиваемой совместной последовательности проектных и режимных параметрических характеристик СРП. Тем самым производится параметризация искомых УВ и последующая точная (в рамках исследуемых моделей) редукция к существенно более простым по сравнению с исходными специальным конечномерным задачам математического программирования, решение которых может быть выполнено применительно к их типичным и некоторым новым постановкам с помощью разработанного авторами конструктивного вычислительного алгоритма («альтернансного» метода), использующего фундаментальные закономерности соответствующей предметной области (ПрО) [8-10]. Подобный подход позволяет реализовать соответствующую программную стратегию оптимального проектирования СРП для достаточно широкого круга ответственных производственных объектов.
Представляющая большой самостоятельный интерес традиционная задача поиска оптимальных программных временных или пространственно-временных УВ в условиях наличия необходимого объёма априорной информации о свойствах объекта может рассматриваться в качестве частной модификации общей задачи оптимального проектирования с заранее фиксируемыми значениями параметрических характеристик СРП.
Особое значение в последнем случае приобретает актуальная проблема синтеза оптимальных регуляторов с обратными связями, автоматически реализующими оптимальные режимы функционирования СРП в условиях воздействия на объект внешних и параметрических возмущений (проблема разработки позиционных стратегий управления). Достаточно эффективная процедура её решения в целом ряде типичных ситуаций может быть построена на основе результатов предварительного решения задачи программного управления.
В настоящей статье приводится систематизированное изложение и обобщение предлагаемых авторами конструктивных методов разработки программных стратегий принятия решений для достаточно широкого круга типовых и новых постановок задач оптимального проектирования СРП.
-
1 Математические модели объектов оптимального проектирования систем с распределёнными параметрами
Для широкого класса СРП модель поведения управляемой величины Q в зависимости от времени t и пространственных координат X е V, X = (xi), i = 1, m; 1 < m < 3, в пределах од- носвязной области V с кусочно-гладкой границей S описывается неоднородным скалярным или векторным операторным уравнением
-
(1) Ц [ Q ( X , t , g ( X ) , d ) ] = f . ( X , uv ( X , t ) , w 1 ( X , t )) , X e V , t > 0,
с граничными
-
(2) L 2 [ Q ( X , t , g ( X ) , d ) ] = f 2 ( U s ( X , t ) , w 2 ( X , t )) , X e S , t > 0
и начальными условиями
-
(3) L з [ Q ( X , t , g ( X ) , d ] = f з ( X ) , X e V , t = 0.
Здесь uV ( X , t ), X e V и U S ( X , t ), X e S - зависящие от X и t (пространственновременные) или только от t (сосредоточенные) соответственно внутренние и граничные режимные управляющие воздействия; g(X ), X e V - пространственно распределённые (статические) управляющие воздействия, в роли которых рассматриваются искомые проектные решения СРП; w = ( Q ( X ,0 ) , d , W 1 , w 2 ) - вектор неопределённых факторов, к которым могут относиться начальное состояние объекта Q ( X ,0 ) , неопределённости параметрических характеристик объекта d и внешние возмущающие воздействия w 1 и w 2 ; L 1 , L 2 , L 3 - заданные (в общем случае нелинейные) интегро-дифференциальные операторы; f _ ( • ), f , ( ■ ), f 3О - известные скалярные или векторные функции своих аргументов, удовлетворяющие обычным требованиям по их гладкости, и V - открытая часть области V , не содержащая её границу.
Краевая задача (1)-(3) может быть решена относительно управляемой величины Q ( X , t ) с требуемой точностью известными численными или в частных случаях аналитическими методами.
В типичных условиях ограниченности ресурсов на формирование УВ и интервального характера неопределённых факторов будем далее считать, что допустимые значения УВ стеснены на всём протяжении процесса управления при t e [0, T ] ограничениями
-
(4) U v ( X , t ) e U v ( X , t ); U s ( X , t ) e U s ( X , t ), t e [0, T ], g ( X ) e G ( X )
с известными границами заданных множеств UV , U s , G , а вся информация о векторе w исчерпывается условиями его принадлежности заданному множеству W его компонентов
-
(5) w ( Q ( X ,0 ) , d , w i ( X , t ) , w 2 ( X , t )) e W ( X , t ) , t e [ 0, T ] .
Каждому фиксированному значению it e W в (5) при любом допустимом согласно (4) конкретном наборе управлений UV , Us и g ( X ) отвечает соответствующее пространственновременное распределение Q ( X , t , uV , uS , g , iw) («изолированная» траектория [11]) управляемого состояния СРП. Объединение этих состояний по всем допустимым величинам w e W при одних и тех же УВ образует ансамбль траекторий объекта в рассматриваемых условиях ограниченной неопределённости [11]
-
(6) Q ( X , t , U v , u s , g , T , W ) = U { Q ( X , t , U v , us , g , T , w : w e W , t e [ 0, T ] ) } .
В рамки описания (1)-(6) укладывается ряд наиболее характерных последовательно усложняемых частных ситуаций, на основе которых может быть сформирована технология принятия решений для различных вариантов постановок общей задачи оптимального проектирования СРП.
В качестве типичной базовой модели обычно используется детерминированная модель СРП без учёта неопределённых факторов в (1)-(3) с априори заданным проектным решением объекта и искомыми режимными управлениями uV, us, выделяющими соответствующую изолированную траекторию из ансамбля (6) при заведомо фиксируемых величинах w е W и g е G [1-3, 8]. Подобная модель предусматривает последующее решение частной задачи оптимального проектирования процессов функционирования СРП при полном объёме необходимой информации о характеристиках объекта.
Детерминированная модель СРП (1)-(3) при w = w е W ; u V = ~ V , uS = us может быть использована для поиска оптимальных проектных решений g ( X ) в условиях заранее фиксируемых режимных УВ n V , uS , в частности, применительно к статическим режимам работы СРП при d Q / д t = 0 в (1)-(3).
В более общей ситуации, требующей организации совместного поиска проектных и режимных решений, следует использовать модель (1)-(3) при w = w с искомыми величинами u V , uS и g . Фиксация только составляющих w 1 и w 2 в каждой из указанных частных моделей приводит к описанию объекта в условиях интервальной неопределённости начального состояния и параметрических характеристик объекта и отсутствия неопределённых внешних возмущений при w = ( Q ( X ,0 ) , d , w 1 , w2 ) .
Аналогичным образом приходим к модели СРП с фиксированными параметрическими характеристиками d в условиях воздействия множественных возмущений w 1 ( t ), w 2 ( t ), полагая в (1)-(3) w = ( Q ( X ,0 ) , ~ ; w 1 , w 2 е W ) [12, 13].
В двух последних случаях соответствующим образом «сужается» ансамбль траекторий (6).
-
2 Детерминированная задача оптимального проектирования программных управлений режимами функционирования СРП
Рассмотрим базовую частную задачу поиска программных оптимальных управлений u V , u S применительно к динамической модели СРП (1)-(3) с полным объёмом априорной информации о проектных решениях g , параметрических характеристиках объекта d и внешних воздействиях w ~ 1 , w ~ 2 в условиях
-
(7) w = w е W ; g = g е G .
Искомые управляющие воздействия в большинстве случаев стесняются лишь известными пределами их возможных изменений
-
(8) uV min < uV ( X , t ) < uV max ; uS min < uS ( X , t ) < uS max , t е [0, T ],
непосредственно характеризующими допустимые множества U V ( X , t ) и U S ( X , t ) в (4).
В соответствии с типичными технически реализуемыми условиями по достижению с допустимой погрешностью заданного состояния СРП в конце процесса управления, для большинства представляющих наибольший интерес прикладных задач необходимо обеспечить за время Т приближение Q ( X , T ) к требуемому пространственному распределению управляемой величины Q ** ( X ) с оцениваемой в равномерной метрике допустимой точностью s > 0 :
-
(9) maxi Q ( X , T ) - Q ** ( X )| < 8 .
X е У
Качество процесса управления оценивается в достаточно общем случае по величине I 1 максимума по r -мерному векторному параметру y e Y с Er функционала I , являющегося заданной числовой функцией своих аргументов
-
(10) 1 1 = max I ( Q ( X , t ), U y , us , g , w , T, y ) ^ min . y e Y U y G Uy- , U s g U s
В схему (10) укладываются типичные задачи оптимизации СРП по критериям быстродействия, энергопотребления, минимизации на V э X отклонений Q(X , t ) от Q ** ( X) в различных метриках [8, 9].
Исследуемая проблема сводится к определению стесненных ограничениями (8) УВ u V , u S , которые переводят объект (1)-(3) в условиях (7) из заданного начального в требуемое конечное состояние согласно (9) при минимальном значении критерия оптимальности (10).
В ряде частных случаев данная задача рассматривается в условиях перевода требования (9) в критерий оптимальности вида (10) при y = X :
-
(11) 1 1 = maxi Q ( X , T , U y , U s ) - Q ** ( X ) ^ min X e V uV , uS
-
2.1 Параметризация управляющих воздействий
-
2.2 Редукция к задаче полубесконечной оптимизации
без ввода дополнительных ограничений на конечное состояние объекта [8, 9].
Структура искомых программных управлений u * ( X , t ), u S ( X , t ) для широкого круга задач оптимизации СРП может быть установлена с использованием известных аналитических условий оптимальности [1-3, 8-10]. Указанным путём во многих случаях может быть получено параметрическое представление этих воздействий с точностью до вектора А ( N ) = (А^ ) ), i = 1, N , определённым образом упорядоченной последовательности конечного числа N параметров А^ N ) , A ( 2 N ) ,..., A ( N ) , непосредственно характеризующих управляющие воздействия в пространственно-временной области их определения (« А ( N ) -параметризация»).
В целом ряде прикладных задач изначально требуется найти управляющие воздействия в заданном классе А ( N ) -параметризуемых функций согласно исходным требованиям, диктуемым техническими возможностями их реализации.
Если непосредственное осуществление операции А ( N ) -параметризации становится затруднительным, то она может быть реализована путём построения конструктивной процедуры отображений на множество Q N допустимых значений А ( N ) параметров более общей природы, в роли которых выступает, например, применительно к сосредоточенным управляющим воздействиям, набор финишных значений первых N переменных бесконечной системы сопряженных уравнений принципа максимума Понтрягина при равных нулю конечных значениях остальных её компонент (« у ( N ) -параметризация») [10].
Интегрирование в аналитической или численной форме уравнений модели объекта (1)(3), (7) с А ( N ) -параметризованными управлениями uV ( А ( N ) , X , t ), uS ( А ( N ) , X , t ) позволяет получить конечное состояние объекта Q ( X , T ) в (9) и значение критерия оптимальности I в
-
(10) в форме явных зависимостей Q ( X , А ( N ) ) и I ( у , A ( N ) ) от своих аргументов. При этом минимально достижимые в классе таких управлений значения s ^ N ошибки s равномерного приближения Q ( X , T ) к Q ** ( X ) в (9)
(12) = min
A ( N > eQ n
{ m an] Q ( X , A ( N ’ ) - Q "( X ) }
X ∈ V
не возрастают (как правило, монотонно убывают) с ростом N е {1, р } [9]
-
(1) > F(2) > > F(p) = F „ > О (1J) £ min > £ min > ... > £ min s inf ,
характеризуя сужающееся к Q ** ( X ) семейство целевых множеств для s = s m j in , j = 1, р в (13). Здесь точная нижняя грань s inf достижимых по условию (9) значений s в цепочке неравенств (13) оказывается равной минимаксу ^П , где р = ю при s inf = 0 и р<« при s inf > 0 соответственно для управляемых и неуправляемых относительно Q ** ( X ) объектов [1, 8, 9].
В широком классе задач А ( N ) -параметрической оптимизации оптимальные управляющие воздействия n V , и * в соответствии с (13) характеризуются минимально возможной для заданного значения s в (9) размерностью N = N 0 вектора А ( N ) по определению минимакса в (12) [8-10]:
-
(14) N 0 =uvs : s min <s<s m,i - 1) , ие {1, р }.
Отсюда, в частности, следует, что для всех достижимых значений s > 0, удовлетворяющим неравенствам (14), А ( N ) -параметризация оптимальных управлений оказывается конечномерной.
В результате А ( N ) -параметризации производится точная редукция исходной задачи, согласно (9), (10), (12), (13), к задаче полубесконечной оптимизации (ЗПО) на минимум функции 1 1 ( А ( N 0) ) конечного числа переменных A N 0) , i = 1, N 0 , с бесконечным числом ограничений, диктуемых требованием (9) для всех X е V [8, 9]:
1 1 ( A ( N 0 ) ) = max I ( y , A ( N 0 ) ) ^ min ;
У e Y A ( N 0 ’ eO n 0
ф ( а ( N 0 ’ ) = max
X e V I
I Q ( X , A N 0 ’ ) - Q * ( X )
< ( N 0’ < г. < (NN 0 -1) М < л
- 6 ; 6 min - 6 < 6 min , N 0 - р -
-
2.3 Альтернансный метод в задачах параметрической оптимизации СРП
Решение целого ряда ЗПО вида (15), (16) может быть найдено конструктивным альтер-нансным методом, распространяющим на ЗПО результаты теории нелинейных чебышёвских приближений [14, 15] в условиях некоторых малостеснительных для многих прикладных задач допущений [8, 9]. Метод базируется на специальных свойствах вектора А ( N 0) оптимальных решений ЗПО (15), (16), установленных при указанных допущениях с использованием упрощённых, по сравнению с известными, альтернансных форм необходимых условий экстремума в задачах недифференцируемой оптимизации и дополнительной информации о конфигурации на V э X и Y э у пространственного распределения Q ( X , А ( N 0) ) и I ( у , А ( N 0 ) ), диктуемой закономерностями ПрО исследуемой конкретной задачи.
Согласно этим свойствам, одинаковые значения I(y,A(Nо)), равные I1(A(Nо)) в (10), и максимально допустимые отклонения Q(X,Д(Nо)) -Q**(X)|, равные е, достигаются в некоторых точках, соответственно yV е Y, v = 1, Ry , и Xо е V, j = 1, RX , суммарное число которых оказывается равным числу всех неизвестных в ЗПО (15), (16), включая ANо), i = 1,N0 , величину I1(A(Nо)) и минимакс етП), если е = етП), в соответствии со следующими соот ношениями [9]:
-
(17) R y + R x = N о + 1 , если £< п о) < е < е ;
-
(18) r x = N о + 1, если е = е^ ) ;
-
(19) R y = N о + 1, если е> ~ ,
где
-
(2о) ~ = Ф 1 ( A ( N о ) ) ; Д ( N о ) = arg ( N о пГ I 1 ( Д ( N о ) ) .
Утверждение (17), дополненное условиями существования экстремума функций
I ( у , Д ( N о) ) и Q ( X , Д ( N ) ) - Q ** ( X ) соответственно в точках y v е int Y , q = 1, R 1 , и q y
Xо е int V, p = 1, RX 1, приводит при заданной величине е в (16) к определяющей системе p равенств
_ _ бЦу о ,Д( N о))
I ( у о , Д ( N о ) ) = 1 х< & N о ) ); * = о;
дУ v = iR; q = jR"; Ry 1 < Ry; yv°q е {yv0};
|Q(Xо, AN•>) -Q"(X")| = е; X (q(x,Д При наличии дополнительной содержательной информации о конфигурации распределения I (y, Д(N о)) на Y э y иQ(X, Д(Nо)) - Q**(X) на V э X в зависимости от величины е, позволяющей идентифицировать точки X о и yv°, данные равенства редуцируются к системе H + H1 уравнений с H + H 1 неизвестными, где H = RX + Ry = Nо+1, H 1 = rRy 1 + mRX 1, а в роли неизвестных фигурируют Nо составляющих A(Nо),i = 1,Nо, вектора Д(Nо); минимакс 11(Д(Nо)); rRy 1 координат Ry 1 точек yV экстремума I(y, Д(Nо)) на Y и mRX 1 координат RX 1 точек Xо экстремума разностиQ(X, Д(Nо)) - Q**(X) на V. p Подобным образом случай е = ето) в соответствии с утверждением (18) приводит при RX = Nо +1 к системе Nо + mRX 1 +1 уравнений (22) с Nо + mRX 1 +1 неизвестными A(-Nо),Xо p и 8^0), а при 8 > ~ на основании (19) получаем для Ry = N0 +1 систему N0 + rRy 1 +1 уравнений (21) с N0 + rR 1 +1 неизвестными А^о),у0 и I1(А(Nо)). yq Для модификации задачи (15), (16) с непрерывно дифференцируемой целевой функцией 11(А(Nо)) = I(А(Nо)), образуемой в частном случае, когда I(у, А(Nо)) не зависит от у, только число RX точек X0, j = 1,RX , становится равным числу искомых значений А^о), i = 1,N0и СтО) в случае 8 = 8^0), а соответствующая система равенств (17)-(19) упрощается следующим образом: (23) rx = N0, если 8N) < 8< Cn-1); (24) RX = N0 +1, если 8 = 8т0). В данном случае равенство (23) аналогичным путём приводит к системе N0 + mRX 1 уравнений (22) с N0 + mRX 1 неизвестными А(№0), X0 для заданного значения 8 > 8тп0), а p случай (24) совпадает с (18). В частном случае (11) задача полубесконечной оптимизации (15), (16) сводится к минимаксной задаче нелинейных чебышёвских приближений (25) Ц(А(N0’) = maxiQ(X, А(N0’)- Q**(X)| ^ min XeV I I А(N0’eQN0 без дополнительных ограничений с последующей редукцией, подобно предыдущим вариантам, равенств (22) в условиях (24) при 11(А(N0)) = 8(Nn)к расчётной системе уравнений. Решения относительно указанных неизвестных систем уравнений, конструируемых по специально разработанной вычислительной процедуре в зависимости от величины 8 в (16) на основании равенств (21), (22) [8], содержат искомые решения ЗПО (15), (16) и могут быть найдены стандартными численными методами. Специфическая проблема редукции соотношений (21), (22) к расчётным системам уравнений во многих случаях может быть решена с привлечением закономерностей ПрО исследуемой задачи управления СРП, позволяющих априори выявить характер поведения на множествах Y э у и V э X функций I(у,А(N0)) и Q(X,А(N0)) -Q**(X) для заданных значений 8 и идентифицировать точки X0, yV в (21), (22). В частности, в [9] установлены все возможные варианты формы этих распределений применительно к характерным условиям Q**(X) = const, Q(X,0) = const при 8 = [8^, 8inf] в базовых задачах оптимального по быстродействию и расходу энергии управления нестационарными температурными полями, описываемыми уравнениями теплопроводности различной пространственной размерности вида (1)-(3) в областях V канонической формы с типичными внутренними и граничными управляющими воздействиями. Процедура параметризации УВ, редукция исходной задачи оптимизации к ЗПО и технология её решения альтернансным методом существенно усложняются при использовании векторных УВ (в частности при совокупном применении внутренних и граничных управлений) за счёт возникновения специфической проблемы выстраивания в однозначно фиксируемом порядке конкретной последовательности параметров А(^), i = 1, N с присвоением каждому из них заранее определяемого номера i e {1, N} , не меняющегося для всего ряда натуральных значений N = 1,р. В зависимости от каждого из формально возможных вариантов такой последовательности изменяются величины минимакса в (11), члены цепочки неравенств (13) и размерность N0 искомого решения Δ(N0) ЗПО. В типичных для приложений задачах со скалярными внутренними или граничными УВ подобная проблема достаточно просто решается с использованием закономерностей ПрО [8, 9]. Описываемая схема алгоритмически точного решения краевых задач оптимального управления линейными и нелинейными моделями СРП параболического типа альтернансным методом апробирована при поиске Δ(N) - и ψ(N) -параметризованных сосредоточенных и пространственно-распределённых УВ в задачах оптимизации по ряду базовых технико-экономических критериев применительно к различным процессам технологической теплофизики, в том числе, с учётом фазовых ограничений на температурные и термонапряжённые состояния в процессе управления и других особенностей промышленных технологий [8, 9, 16]. Предлагаемая технология предварительной параметризации искомых УВ, конечных состояний объекта и критерия оптимальности, последующей процедуры точной редукции к ЗПО, разрешаемой с использованием альтернансных свойств искомых экстремалей и дополнительной информации о закономерностях ПрО, распространяется далее на значительно более широкий круг задач оптимального проектирования детерминированных и не полностью определённых моделей СРП. Ниже рассматриваются наиболее характерные постановки таких задач, сводимые к ЗПО различного вида, решения которых укладываются в общую схему (15)-(16) альтернансного метода. 3 Детерминированная задача оптимизации проектных решений в условиях заданных режимных управлений Данная частная задача оптимального проектирования СРП сводится к поиску статического распределённого управления g*(X) ∈G,которое переводит объект (1)-(5) в условиях фиксированных воздействий w = w~ ∈W и режимных управлений uv = u~v, us = u~s в требуемое конечное состояние согласно (9) с минимальным значением критерия оптимальности (26) I2=maxI(Q(X,t),u~v,u~s,g(X),w~,T, y) → min y∈Y g∈G вместо (10). Искомое проектное решение g*(X) может быть найдено по описанной выше общей схеме определения режимных управлений uv*и us*путём редукции исходной задачи к ЗПО вида (15), (16), разрешаемой теперь уже относительно вектора Δ(gN g) = (Δ(iNg)),i = 1,Ng , параметрического представления g*(X) I (A(Ng0’) = max I(y, A(Ng0’) ^ min ; g y^Y g A^g 0 ’eQg 0 Ф2(A^g0’) = max Q(X, A^g0’)- Q**(X) < 8; 8mN0’ < 8< ^N0-1’ Представляющая самостоятельный интерес задача оптимизации проектных решений объекта на стадии его функционирования в стационарном состоянии Qc(X ) при (28) lim dQI dt = 0; lim uv = const; lim us = const t→∞ t→∞ t→∞ во многих случаях сводится к виду (11) (29) I^ = maxiQ (X, g(X)) - Q**(X)| ^ min . X eV g (X )eG Процедура A^g)-параметризации g(X), аналогичная A(V)-параметризации режимных управлений, приводит к параметрическому представлению g(X, AN)), Qc (X, AN)) и 12(A(Ng)) управляющего воздействия, стационарного состояния СРП и критерия оптимальности. Последующая редукция к нелинейной задаче чебышёвских приближений вида (25) I (^g0)) = max Q (X, A('Vg0)) - Qi X) ^ g X∈V c g min к(Ng 0) Ag e“ Vg 0 позволяет найти ее решение AgNgо)с требуемой точностью по схеме альтернансного метода. Специфической особенностью задачи (30) является необходимость попутного определения границ области G в (4), исходя из фундаментальных законов сохранения энергетического или материального баланса в стационарном режиме работы СРП. 4 Детерминированная задача совместной оптимизации проектных решений и режимов функционирования СРП Общая детерминированная задача оптимального проектирования СРП (1)-(5) в отличие от рассмотренных в разделах 2 и 3 заключается в совместном определении допустимых проектных решений g*(X) и режимных управлений п* и u*, обеспечивающих в условиях известного вектора w = w e W достижение требуемых согласно (9) конечных состояний объекта (1)-(5) с минимальным значением критерия оптимальности (31) Iз = max I(Q(X, t), uy, us, g, -w, T, y) ^ min yeY Uv,Us,g вместо 11,12 в (10), (26) и (29). Процедура A(V) и A(Ng)-параметризации искомых воздействий uv, us и g(X) соответственно, формирование расширенного вектора параметров повышенной размерности A(N+Vg) = (AV),A(Ng)) и последующее интегрирование уравнений модели объекта (1)-(5) с параметризованными управлениями uv (A(V), X, t),us (A(V), X, t), g(X, A(Ng)) приводят к пара-(V+V) (V+V) метрическим зависимостям Q(X, Azg ), I (y, Azg ) конечного состояния объекта и критерия оптимальности (31) от своих аргументов. В результате опять обеспечивается редукция исходной задачи к ЗПО вида (15), (16): I3 (A(;0 + Vg0)) = max I(y, A(;0+Vg0)) ^ min ; 3 1 yeY A^0+Vg0’eOv0+Vg 0 Ф,(A.V0+v-0’) = maxQ(X,A.V0+v-0’)-Q"(X) < £; s*V0+Vg0’ < s< s*V0+Vg0-1), X∈V (или в частных случаях, подобных (11), к ЗПО вида (25), (30)), снова разрешаемой по общей предлагаемой схеме относительно искомой величины A(;0 + Vg0). Здесь размерность V0 + Vg0 вектора A(;0 + Vg0) опять определяется по правилу аналогичному (14) применительно к по- добной (13) цепочке неравенств для величин минимаксов, определяемых согласно (12) с заменой N на N + Ng . Векторный характер искомых управлений приводит к необходимости решения с помощью закономерностей ПрО, указанной в разделе 1, вспомогательной задачи формирования упорядоченной последовательности компонентов вектора (N+N„) /A(N+N„) .(N+N„) .(N+N„) A2g = (A21g , A22 g ,..., Az(N+N ), число N + Ng которых увеличивается с возрастанием N и Ng. 5 Задача оптимизации проектных решений СРП в условиях интервальной неопределённости параметрических характеристик объекта Самостоятельный интерес представляет задача оптимального проектирования СРП (1)(6) в характерных условиях интервальной неопределённости вектора b = (d, Q0) = (dj, j = 1, r; Q0) e W1 c W неизменных во времени параметрических характеристик объекта, к которым во многих случаях можно отнести параметрическое представление начального состояния объекта Q(X,0) = Q0 = const VX e V , где (33) W1 = dj,Q :djmin < dj < djmax; Q0min < Q0 < Q,_, j = 17}. При заданных внешних воздействиях W1, W2e W требования вида (9) должны быть выполнены для всех конечных состояний ансамбля (6) (34) Q(X,T,u,,us,g, W) = U{Q(X,T,u,,us,g, WnW2,b e W1 c W)}, образуемого всеми допустимыми согласно (33) реализациями значений b : (35) max [maxiQ(X,T,b) - Q**(X)|] < £. beW1 XeV । । В таком случае задача сводится к совместному определению uv*,us*, g*, обеспечивающих при w1 = v~i, w2 = W2 перевод ансамбля траекторий (6) в требуемое конечное состояние (35) с минимальным значением функционала качества I4, определяемого по принципу гарантированного результата в аналогичной (10) форме функции максимума: (36) I4= max I(Q(X, t), u,, us, g, "W1, W2, b) ^ min . beW1 uv,,us,g Подобная (27) A(N+Ng) -параметризация искомых воздействий приводит к редукции исходной задачи (35), (36) к ЗПО вида (32) с r +1 -мерным векторным параметром y = b I4 (4N0+Ng 0)) = max I (b, A(N0+Ng 0)) ^ min ; 4 1 beW1 2 A*N0+Ng 0 >eO n0+Ng 0 Ф 4(A(ZN°+Ng) ) = max Q (z, A(”0 + Ng 0) ze Z ) - Q**(X) < £; £m’ (N0+Ng 0) < <N0+Ng 0 min ~ £< £ min -1). ; z = (X,b); Z = V x W1 e Em+r+1 и континуумом ограничений, рассматриваемых на расширенном по сравнению с (32) множестве Z элементов z e Z, включающем наряду с пространственными переменными X e V допустимые значения вектора b e W1. Возникающая при этом дополнительная проблема выявления характера распределения Q(z, A(N0+ Ng0)) -Q**(X) на множестве Z в целях редукции системы равенств вида (21), (22) к расчётным системам уравнений альтернансного метода во многих случаях может быть решена на основе свойств результирующих состояний СРП для детерминированных состояний объекта и фундаментальных закономерностей ПрО [8-10, 16]. В наиболее характерных ситуациях точки z0 = (xо, bо), j = 1, Rx, в которых выполняются подобно (22) равенства Q(z 0, AN0 + Ng0)) - Q**(X j ) = £ , содержат комбинации предельно допустимых значений dj на границах множества W1 6 Программная реализация обратных связей в задачах оптимизации режимов функционирования СРП при наличии внешних возмущений В типичных условиях воздействия на реальный объект с заданными проектными решениями g = g e G в (4) и заранее фиксируемыми параметрическими характеристиками d = d e W1, множественных возмущений w1, w2 e W в (5), вся информация о которых исчерпывается заданием их граничных значений в пределах допустимой области W их изменения, * * возникает задача поиска оптимальных программных управлений uv , us ансамблем траекторий ~ ~ Q(X,t,uv,us,g,T,d, W) = U{Q(X,t,uv,Us,g,T,d, Q0, W1, W2 e W)}, t e [0,T]. Эта задача может быть записана в подобной (35), (36) форме max [max Q(X, T, Q0, W1, w2 ) - Q (X)] < £; Q0, w1, w2eW X eV ~ I5 = max I (Q(X, t), uv, us, g, d, Qo, w, w2) ^ min Q0,W1,w2 eW Uv ,Us с последующей редукцией после параметризации искомых управлений к ЗПО вида (37): Т (Д(N0)Л — Л<N0) ла) ла) 1 х min I 5 (AZ ) = maxI(Az ,Q0, w1, w2 ) ^ . .min Q0, иц w2eW A(N0’eQ N0 (N0) (N0 ) ** (N0 )
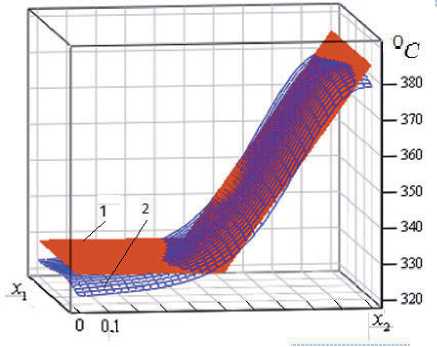
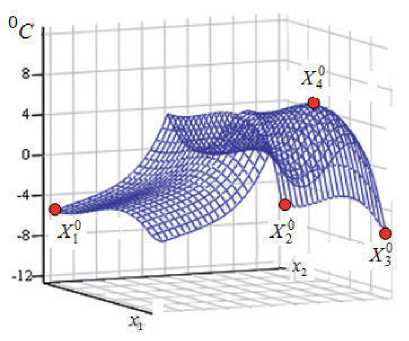
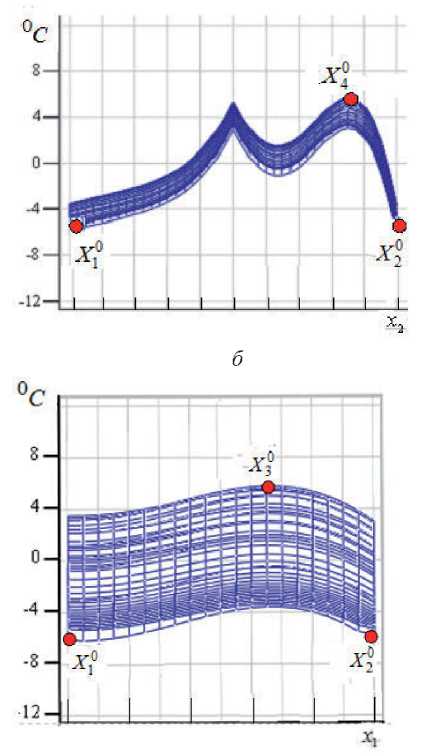
(41) ф 5 (AZ ) = max Q(z 1, AZ ) - Q (X ) < £; £nin < £ < £nin , Z1e Z1 z 1 = (X,Q0,w1,w2); Z1 = Vx W2; W2 = (Q0,w1,w2) e W. Описанная стратегия программного управления по принципу гарантированного результата ансамблем траекторий СРП, порождаемым всеми допустимыми реализациями учитываемых возмущающих воздействий, заведомо приводит к существенным потерям по миними- зируемому критерию качества по сравнению с замкнутыми системами автоматического управления, обеспечивающими требуемый уровень подавления возмущений. Однако проблема синтеза соответствующих оптимальных автоматических регуляторов отличается известными затруднениями принципиального характера [11, 13]. Возможный путь их преодоления состоит в переходе от трудноразрешимой задачи построения в явной форме алгоритма оптимального управления с обратными связями к поиску реализующей искомый закон регулирования последовательности программных оптимальных управлений uVk(X,t),u*sk(X, t), t e [tk,T],0 < tk < T, для каждого из которых начальное на ин- тервале [tk, T] состояние ансамбля Q(X, t, uv, u , g, T, d, W) в (38) вычисляется в заранее s t=tk фиксируемые на временной сетке с заданным периодом квантования h моменты времени tk = kh,k = 0,с-1,сh = T по сигналам Qu(X,tk) измерения текущего состояния объекта с помощью известных способов его наблюдения [12, 13]. В таком случае исходная минимаксная задача оптимизации (39), (40), сформулированная на всём временном промежутке [0, T], сводится к последовательно разрешаемым на интервалах [tk,T] э t,к = 0,с-1, задачам вида (39), (40) программного управления «суживающимися» по мере возрастания tk ансамблями траекторий Q ( X, t, uVk, uSk, g, T, d, w1 k, w2k ); w1 k,, w2k e W, t e [tk, T ], с наблюдаемыми начальными состояниями Qu (X, tk ). При этом искомые оптимальные управления u*, uS на всём протяжении процесса управления компону-* * ются из участков изменения uVk, uSk на промежутках [tk, tk + h ]: u* = {uk,t G [tk,tk + h]};u* = (u*,uS);uk = («*k,uSk); tk = kh; k = 0, с -1; сh = T. Построение uk в каждой позиции (tk, Qu (X, tk )) по существу формирует закон управления с обратной связью uk* (tk, Qu (X, tk ) . Если вычисление uk производится за время, не превышающее достаточно малого периода квантования h , то этот закон реализуется с шагом h : (43) uk( tk + h ) = uk*( tk, Qu (X, tk )), обеспечивая тем самым последовательную отработку алгоритма (42) в реальном времени. При этом в условиях h ^ 0 получаем в соответствии с (42), (43): (44) u* = u**(т,Qu (X,t))Vtg (0,T). Дальнейшая процедура A(Nk)- и A(N)- параметризации искомых управлений uk и u* соответственно приводит по предлагаемой общей методологии к последовательному решению с шагом h ЗПО вида (41) 11 k (^Nk 0), tk ) = ,maxIk (^Nk 0), Q 0, tk , w1 k , w 2 k ) ^ (Nmin; Q0, w1 k, w2 k A(e0 k 'eO Nk0 (45) Ф 1 k (AN0), tk) = max Q(z 1 k, <0k), tk) - Q** (X) < г(k); z1 keZ1 k 1 k = 0,^-1; z 1 k = (X, Q0, W1 k, w2k ); Z1 k = V x W2k; W2k = (Q0, W1 k, w2k) G W с зависящим от tk континуумом ограничений Ф1 k (A(Nk0), tk ) на конечное состояние объекта при последовательном уменьшении влияния на него интегрального эффекта воздействия возмущений w1 k, w2k e W2k, на промежутках t e [tk, T] при tk ^ T . Здесь явные зависимости Q(z1 k, A(Nk0),tk) и Ik(A(Nk0),Q0,tk, w1 k, w2k) от своих аргументов должны быть получены после интегрирования уравнений модели объекта (1)-(3) с измеряемым начальным состоянием Q(X,tk) = Qu(X, tk) вместо (3) при А(Nk) -параметризованном управлении uk . В соответствии с требованием (39) ошибки равномерного приближения s(k), k = 0, с -1, в (45) должны выбираться таким образом, чтобы обеспечить выполнение соотношения а(с-1) < s. По найден- ным оптимальным значениям Δ(ΣNk0) вычисляются и реализуются на объекте, согласно алгоритму (42), параметры Δ(ΣN0) оптимальных управлений uV* и u*S . 7 Оптимальное проектирование объектов технологической теплофизики В качестве примера, представляющего самостоятельный интерес, рассмотрим детерминированную задачу оптимального проектирования установки градиентного индукционного нагрева (ИНУ) цилиндрических слитков из алюминиевых сплавов перед последующей операцией прессования в ответственных технологических комплексах обработки металла давлением [16]. Температурное поле Q(x1,x2) в процессе индукционного нагрева описывается в зависимости от времени t∈[0,T] , радиальной x1 и продольной x2 координат в области V = (x1 е [0,1], x2 е [0,1]) двумерным неоднородным уравнением теплопроводности в относительных единицах вида (1) с начальными и граничными условиями (2), (3) третьего рода и заданным законом пространственного распределения внутренних источников тепла, определяемым известным решением уравнений Максвелла для электромагнитного поля индуктора. Градиентный нагрев слитка с положительным перепадом конечной температуры Q(x1,x2,T) по его длине x2в направлении прессования, который обеспечивает существенное повышение производительности пресса, осуществляется в ИНУ двухсекционного исполнения (рисунок 1) [16]. В качестве внутренних сосредоточенных УВ uV (t) используются суммарные удельные мощности внутреннего тепловыделения в обеих секциях uV (t) = (uV1(t),uV2(t)), подчиненные ограничениям вида (8): Рисунок 1 – Конструкция двухсекционной ИНУ периодического действия: 1– секция индуктора; 2– заготовка (46) 0< uv 1(t) < uvimax; 0< uv2 (t) < uv2max . В роли искомых базовых проектных решений ИНУ заданной двухсекционной конструкции будем рассматривать максимальные мощности секций uV1maxи uV2max, стесняющие возможные пределы изменения режимов УВ в (46), и, следовательно, в данном случае будем иметь для g(X ) в (4): (47) g(X ) = (uV1max, uV2max) = const. В качестве критерия оптимальности в условиях заданной длительности процесса нагрева фиксируемой требуемой производительностью технологического комплекса «ИНУ–пресс» принимается, подобно (11), достижимая точность равномерного приближения конечного температурного состояния к его заданному неравномерному распределению перед последующим прессованием слитка: (48) I* = max Q)(xDx2,T,и, 1 (t),u,2(t),и,imax,u,2max)-Q**(xvx2) ^min . X1, X 2^[0,1]l I uv, g ** Требования к градиентному характеру нагрева слитка приводят к заданию Q (x1, x2) в форме кусочно-линейной функции продольной координаты Q*(1), 0 < x2 < x2; Q **( x1, x 2) = < Q*(1) +Q*(2)- Q*(1) 1 - x 2 (x2 *. * - x2 ), x2 < x2 < 1 с известными постоянными Q*1), Q*2), x2 . Проблема теперь сводится к совместному поиску оптимальных управлений u,1(t), u,2(t) , стесненных ограничениями (46) и проектных решений u,1max,u,2maxв (47), обеспечивающих в совокупности достижение минимального значения критерия оптимальности (48). Данная задача является частным случаем общей детерминированной задачи (31) оптимального проектирования СРП с целевой функцией вида (11). Известные условия оптимальности в форме принципа максимума Понтрягина заведомо определяют u,1(t) и u,2(t) в виде кусочно-постоянных функций времени, попеременно принимающих только свои предельно допустимые значения согласно (46) [1, 8, 9]. Тем самым обеспечивается А(N) -параметризация искомых УВ с точностью до числа N и длительностей А("), i = 1, N, интервалов их постоянства на протяжении процесса управления в условиях свободы выбора Т из условий достижения минимальной величины критерия оптимальности (48). В наиболее просто реализуемых режимах работы ИНУ с синхронным управлением во времени обеими секциями один и тот же вектор А(N) характеризует одновременно оба воздействия и,1 и и,2. N При T = ^А(") для простейшего по условиям технической реализации изначально зада-i=1 ваемого режима работы ИНУ с неизменной во времени максимальной мощностью обеих секций будем иметь Nо = 1, и вектор А(N0) = А1-1тем самым определён с точностью до длительности T = А^1 процесса управления. А("до)-параметризация искомых проектных решений g(X) в данном случае непосредственно описывается их заданием в форме (47) при Ng0 = 2 : (50) А"0)= А® = (А^, Ад2); А® = и, 1„; Ад2 = и,,„„. (No + N„ о) В итоге получаем для совместного вектора искомых параметров АЕ0 g0: (51) N0 + Ng0 = 3; А"0 +Ng0)= А1^) = (А^,и, 1,„,и,2max). Интегрирование (в аналитической или численной форме) уравнений модели при параметризованных управлениях uV(t,А^1)),g(X) = (uV 1max,uV2max) с последующей подстановкой результатов в (48) обеспечивают редукцию к задаче вида (32) без ограничений с целевой функцией, подобной (25) и (30): I*(А”0 +Ng0)) = max Q(xi,x2,А^0 +Ng0))-Q**(Xi,x2) = X1, X 2^[0,1] = max .IQ(xi, x 2, А(11)’ uVimax, uV 2max ) -Q АX1,X 2 )| ^ (1)min• x1,x2e[0,1] А1 , uv 1max, uV 2 max Альтернансные свойства искомых решений AN0 +Ng0)= (А11), uV 1max, uV2max), определяемые в рассматриваемом случае подобно задаче (25) базовыми соотношениями (22), (24) (где надо заменить АN0)на AN0+Ng0)), приводят с использованием известных закономерностей конечного пространственного температурного распределения [8, 9, 16] к следующей системе шести уравнений альтернансного метода, разрешаемой известными способами относительно всех шести искомых параметров оптимального процесса нагрева А11), uv 1max, UV2max sm^n= min I*, X0 = (x0e, x 0 e) включая выступающие в роли промежуточных неизвестных координаты точки экстремума X4: 0дО) ** о (3) . Q(X1 , А1 , uv 1max, uv2max) Q(X 1 ) ^min ; 0 T(l) ** 0(3) Q(X 2, А1 , uV 1max , uV2max ) Q(X 2) 6min ; 0 T(1) ** 0(3) Q(X 3, А| , uV 1max, uV 2max ) Q (X 3) 0 T(1) ** 0(3) Q(X 4, А1 , uV 1max, uV 2max) Q(X 4) 6 min; d 0 дС1)** (53)n(Q(X 4, А1 , uV 1max , uV2max) Q(X 4 )) 0 ox1 d 0 T(1) _ (Q(X 4, А1 , uV 1max, uV2max) Q(X 4 )) 0 dx2 X0= (x.°,x,°.), j = 1,4; x,0,. e {x. :0 < x. < 1};x0, e {x, :0 < x, < 1}; J 1 j 2 j 1 j 1 1 2 j 22 X0 = (0,0); X20= (0,1); X3 = (1,1); X40= (x^, x0e); 0 < x0e< 1; 0 < x0e< 1. Некоторые расчётные результаты, полученные при нагреве цилиндрических слитков из алюминиевых сплавов Д16 (АА2024) в ИНУ двухсекционного исполнения при Т=215°С, приведены на рисунке 2. Заключение Предлагается технология построения программной стратегии принятия решений применительно к широкому кругу задач оптимального проектирования сложноструктурированных систем с распределёнными параметрами, трактуемых как комплексная проблема поиска проектных решений и последующих режимов функционирования объекта, которые обеспечивают в совокупности достижение экстремальных значений совместного критерия качества. Развиваемая в статье методология базируется на предварительных процедурах параметризации УВ, операции точной редукции исходной задачи к специальным задачам математического программирования и конструктивных способах их последующего решения с исполь- зованием альтернансных свойств искомых экстремалей и фундаментальных закономерностей конкретной ПрО. а в Рисунок 2 – Заданное (1) и полученное (2) температурные распределения по объёму заготовки в процессе нагрева в ИНУ (а), отклонение полученного температурного распределения от заданного по объему (в), радиусу (г) и длине (б) заготовки для I * = 60 с : д^ = 184.3 c; UV1max = 2.881 ■ 106 Вт I м3; uV2max = 4.424-106 Вт I м3; x^ = 0.675; x 0 e = 0.853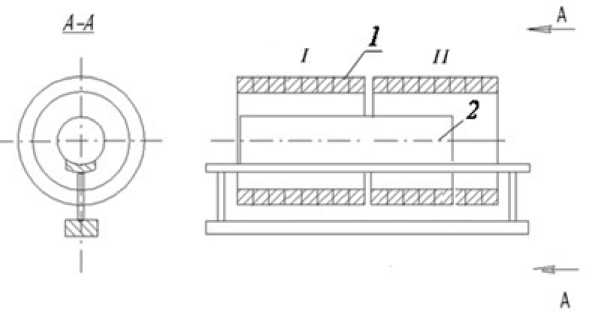
Список литературы Технология оптимального проектирования сложноструктурированных систем с распределёнными параметрами: программные стратегии принятия решений
- Бутковский, А.Г. Теория оптимального управления системами с распределенными параметрами / А.Г. Бутковский. - М.: Наука, 1965. - 474 с.
- Бутковский, А.Г. Методы управления системами с распределенными параметрами/ А.Г. Бутковский. - М.: Наука, 1975. - 568 с.
- Бутковский, А.Г. Оптимальное управление нагревом металла / А.Г. Бутковский, С.А. Малый, Ю.Н. Андреев. - М.: Металлургия, 1972. - 440 с.
- Лионс, Ж.-Л. Оптимальное управление системами, описываемыми уравнениями с частными производными / Ж.-Л. Лионс. - М.: Мир, 1972. - 414 с.
- Лурье, К.А. Оптимальное управление в задачах математической физики / К.А. Лурье. - М.: Наука, 1975. - 478 с.


