Технология укрупнения дидактической единицы при изучении школьной математики

Формирование математических понятий очень сложный и длительный процесс.

Степень усвоения математических понятий во многом зависит от индивидуальных особенностей учащегося и уровня его подготовки, а также в некоторой степени от профессиональных качеств учителя.

При подготовке к уроку для формирования знаний, умений и навыков (независимо от дисциплины) учителю необходимо выбирать способы, которые способствуют всестороннему развитию личности. При выборе способов организации учебной деятельности нужно учитывать тот факт, что работа на уроке должна выполняться не только учителем и группой успевающих учеников, а должна выполняться всем классом. На уроке учитель должен создать такие условия, при которых каждый учащийся становится полноценным участником учебного процесса. Так как задача учителя заключается в том, чтобы мотивировать учащегося на учебу, вызвать тем самым интерес к предмету.

Формирование вычислительных умений и навыков по принципу укрупнения дидактической единицы способствует воспитанию личности с гибким умом, с творческими способностями, умеющей применять полученные знания на практике.

Как известно, усвоение школьных знаний и формирование учебных навыков зависит от уровня умственного развития учащихся. Вся математика, по мнению П.М. Эрдниева, состоит из парных заданий [3]. Традиционная система преподавания математики не всегда придерживается этого принципа и тем самым обедняет логическое мышление. Поэтому формирование математических понятий нужно закладывать укрупненными дидактическими единицами одновременного изучения того или иного понятия. При таком подходе учебный материал усваивается глубже и быстрее, знания становятся прочнее, так как они преподносятся учащемуся сразу крупным блоком в системе внутренних и внешних связей.

Обобщая многолетний опыт учителей в преподавании математики по принципу укрупнения дидактической единицы, можно утверждать, что метод укрупнения дидактических единиц служит проблеме интенсификации методов обучения математике. Академик МАНПО, профессор Селевко Г.К. в энциклопедии по педагогическим технологиям дает обоснование эффективности укрупненного введения новых знаний, описывает возможности метода укрупнения дидактической единицы, позволяющего:

• •    применять обобщения в текущей учебной работе на каждом уроке;

• •    устанавливать больше логических связей в материале;

• •    выделять главное и существенное в большой дозе материала;

• •    понимать значение материала в общей системе "знания-умения-навыки";

• •    выявить больше межпредметных связей;

• •    более эмоционально подать материал;

• •    сделать более эффективным закрепление материала [2].

Метод укрупнения дидактических единиц, впервые разработанный на математическом материале, сейчас приобрел общедидактический статус [4]. Укрупнение, сжатие содержания образования можно производить с помощью различных моделей.

Формирование математических знаний у учащихся осуществляется на уроках математики. При подготовке к уроку учителю необходимо помнить: при освоении знаний укрупненными порциями создаются лучшие условия для возникновения и системного качества знаний. Так, например, по технологии укрупнения дидактической единицы можно изучать взаимно обратные понятия.

Как уже отмечалось, формирование знаний, а, следовательно, укрупнение дидактической единицы должно осуществляться на уроках.

Рассмотрим урок математики в 6-ых классах с применением принципа укрупнения дидактической единицы, объединив взаимно обратные понятия такие, как прямо пропорциональные и обратно пропорциональные величины. В школьной программе эти величины изучаются на разных уроках, и по календарному плану на их изучение отводится 5 часов. Занятия по рекомендуемой технологии были проведены в гимназии № 38 г. Караганды на двух параллелях: 6 "А" - экспериментальный и 6 "Б" - контрольный. Урок проводился с применением слайдовой презентации.

Тема урока: "Прямо и обратно пропорциональные величины" (рисунок 1):

Рис. 1. Тема урока

Цели урока:

• 1.    Сформировать понятия прямо и обратно пропорциональных величин.

• 2.    Научить применять свойства прямой и обратной пропорциональности к решению задач.

• 3.    Развивать логическое мышление учащихся.

• 4.    Развивать интерес к математике.

Ход урока.

• I.    Проверка знаний. Математический диктант (рисунок 2):

Ответы на интерактивной доске скрыты функцией "Непрозрачный экран", после сдачи работ ученики сверяют ответы с ответами на доске.

Рис. 2. Математический диктант

• II.    Объяснение нового материала. Рассмотрим задачи (рисунок 3):

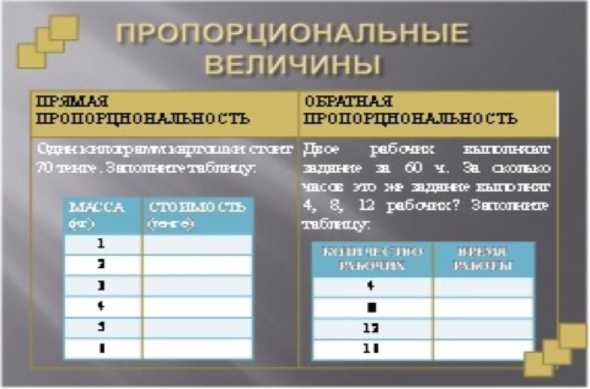
Рис. 3. Текстовые задачи

Сравнив числа, записанные в первой таблице, мы заметим, что во сколько раз увеличивается первая величина (масса), во столько же раз увеличивается и вторая величина (стоимость):

6        420          6420

• 3    и            3. Тогда

  2        140          2140

Если же сравнить числа, записанные в таблице, мы заметим, что во сколько раз уменьшается первая величина (масса), во столько же раз уменьшается и вторая величина (стоимость):

2   1      140   1        2140

и                . Тогда

• 4  2     280  2      4280

Полученные величины называются прямо пропорциональными. Сформулируем теперь определение прямо пропорциональных величин:

Если одна из величин увеличивается (уменьшается) в несколько раз и другая величина увеличивается (уменьшается) во столько же раз, то такие величины называются прямо пропорциональными.

Теперь рассмотрим вторую задачу. Вычислим отношение двух произвольных значений одной величины (количество рабочих) и соответствующих им значений другой величины (время работы):

12            101

• 3,    но

4           303

Отсюда, если количество рабочих увеличивается в три раза, то время выполнения задания уменьшается в три раза. Если одна из величин увеличивается (уменьшается) в несколько раз, а другая величина уменьшается (увеличивается) во столько же раз, то такие величины называются обратно пропорциональными.

Свойства прямой и обратной пропорциональности представлены на рисунке 4.

• III.    Решение примеров (Математика 6 [1]).

• IV.    Подведение итогов. Задание на дом: №№ 123, 125, 174, 176 (рисунок 5).

Рис. 5. Подведение итогов

На отдельное изучение приведенных тем по календарному плану отводится 5 часов. Применяя принцип укрупнения дидактической единицы, учителю удалось сократить количество часов до трех. В то же время качество усвоения не ухудшилось, а, наоборот, повысилось. При таком введении понятий прямой и обратной пропорциональности ученики имеют возможность постоянно производить сравнение между прямо и обратно пропорциональными величинами, видеть их различия, и, следовательно, быстро и правильно определять прямые и обратные величины.

В тех же параллелях по принципу укрупнения дидактической единицы учитель объединила темы "Пересекающиеся прямые", "Перпендикулярные прямые", "Параллельные прямые" и "Прямоугольная система координат", на отдельное изучение которых отводится 6 часов. Объединив темы, то есть, применив принцип укрупнения дидактической единицы, можно сократить временной интервал до 4 часов. Таким образом, в конце учебного года на повторение данных тем у учителя появится больше времени, и эти темы можно пройти повторно.

Применение принципа укрупнения дидактической единицы также проводилось с использованием слайдовой презентации. На отдельных слайдах указаны тема урока (рисунок 6) и цели занятия (рисунок 7).

Рис. 6. Тема урока

ЦЕЛИ УРОКА х Сформировать понятия пересекающихся, перпе ндикуга рных и параглегьных: прямых х Выработать нав ы к построения пересек аюцихся перпендикулярных и парагтгъныхпрямых х Науч ить пр именять получ енные знания на практике.

х Раз в ив атьлогическое м ыш ление учащ ихся.

х Раз в ив ать интерес к матем атик е

Рис. 7. Цели урока

На следующем слайде выписаны вопросы для повторения ранее изученного материала. Для повторения выбрана тема, максимально приближенная к новому материалу, а именно вопросы по масштабу и координатной прямой (рисунок 8).

ВСПОМНИМ ПРОЙДЕННОЕ

• ■    Что нззы вают м зсш тзбом карты?

• ■    Где и для чего используется масш таб?

• ■    В чем отлитие масштабов 150 и 50:1?

• ■    Какую прямую называют координатной пряной?

а В каком направлении изображаются на кооря тэт ной прямой пол ожительны е числам

• ■    В каком направлении изображаются на кооря внятной прямой отриутельные числа?

После повторения материала предыдущих занятий учитель приступает к объяснению новой темы. На одном слайде в параллельной записи представлены три вида расположения прямых (рисунок 9).

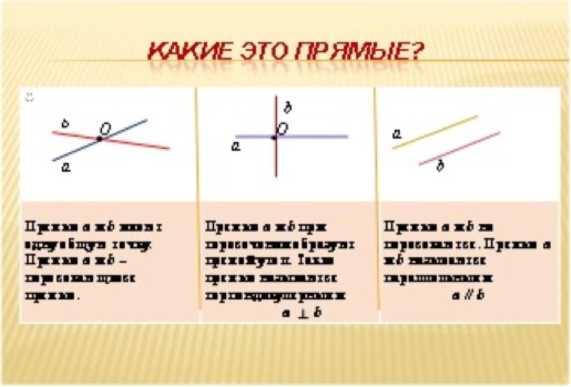
Рис. 9. Три вида расположения прямых

Итак, рассмотрим урок по теме "Пересекающиеся, перпендикулярные и параллельные прямые", составленный следующим образом:

Ход урока.

• I.    Проверка знаний.

Сегодня мы на уроке будем строить дом. Крепкий и надёжный по всем правилам архитектуры. Начнём строительство с фундамента здания. Это основа здания, поэтому он должен быть особенно крепким.

Фундаментом наших знаний является теория. Посмотрим, на сколько прочны наши знания.

Ученики устно отвечают на поставленные вопросы.

• II.    Объяснение нового материала.

А сейчас приступим к построению дома. Стены дома должны пересекаться с полом и потолком дома, и стены мы должны строить перпендикулярно полу, а потолок и пол должны быть параллельны друг другу. Посмотрим, по каким прямым мы должны строить стены и пол, потолок и пол.

Вот теперь мы знаем по каким прямым мы должны возводить стены дома и потолок. Выполняем задания 1 и 2 (рисунок 10).

Рис. 10. Задания

Перпендикулярные прямые делят плоскость на четыре прямых угла. Две перпендикулярные прямые образуют координатную плоскость (рисунок 11).

КООРДИНАТНАЯ ПЛОСКОСТЬ

Ъпжк

• • 3                   | ПлЦибЦИЛП Ш ГПЦ13Ши.й

•2

• -1              А№Дф*11С(-1.ЦЦ41Ц

1085. Стр. 271 №№ 1103 (устно), 1105 [1].

J *2 J ' ^f Н ^ КН. •» МД » Qi » н-д2) ■ -2

2 0)^лткос||П)(к?тфпааОш тпЦС, К

5 Qijcmcocpn^Bjn^ в п^ я vuA.C, Г

Рис. 11. Координатная плоскость

На слайде, изображающем прямоугольную систему координат, дается задание, которое ученики выполняют непосредственно на слайде с помощью интерактивной доски.

Выполняем задания: стр. 261 №№ 1064 (устно), 1066. Стр. 266 №№ 1084 (устно),

• IV.    Подведение итогов (рисунок 12).

• V.    Задание на дом: №№ 1069, 1071, 1090, 1092, 1112 (рисунок 12).

ЧТО МЫ ВЫУЧИЛИ НА УРОКЕ?

Вопрос

Ответ

^р^сйуауаумд^сл нарам <мымьы4и м^рж « д иф^фх ь млм

ЗНАНИЕ НАДОМ: №№10 69.1071.1090.1092.1112.

Если прямыеа и & пересекаются под прямым утлом, то они называются..

Если прямые а и & имеют одну общую точку то они называются,..

Если прямые а и 5» не имеютобщих то чек, то они называются..,

КАКИЕ ЭТО ПРЯМЕЕ?

Рис. 12. Подведение итогов

Преимущество такого представления изучаемого материала в том, что ученики сразу же видят различия в расположении пар прямых. Под рисунками прямых приведены определения пересекающихся, перпендикулярных и параллельных прямых. Здесь же даны обозначения для перпендикулярных и параллельных прямых.

При подведении итогов урока опять же все три вида расположения прямых целесообразно привести на одном слайде в виде таблицы. Так легче будет ученикам запомнить эти виды при сравнении.

После изучения названных тем по принципу укрупнения дидактической единицы было проведено тестирование, которое выявило уровень усвоения знаний учащимися.

На основе диагностических данных учеников можно дифференцировать по следующим выделенным уровням усвоения (таблица 1).

Таблица 1. Уровни усвоения знаний учащимися на начало эксперимента

Уровни усвоения знаний	Баллы	6 «Б» класс (количество учащихся)	6 «А» класс (количество учащихся)
Высокий	9- 10	2 (7%)	2 (7%)
Продвинутый	7 – 8	5 (18%)	10 (33%)
Средний	5-6	11(39%)	10 (33%)
Пониженный	3-4	8 (29%)	8 (27%)
Низкий	0-2	2 (7%)	0

Данные, полученные после первого тестирования, свидетельствуют, что уровни усвоения знаний у учащихся параллельных классов отличаются. Более развиты учащиеся в 6 «А» классе (40% учащихся имеют высокий и продвинутый уровень усвоения знаний).

В 6 «Б» более низкий уровень усвоения знаний: всего 25% учащихся имеют высокий и продвинутый уровень усвоения знаний, тогда как 36% учащихся имеют пониженный уровень усвоения знаний.

Произведя анализ данных, полученных в результате эксперимента можно отметить, что на 8% сократилось количество учащихся с пониженным и низким уровнем усвоения знаний в 6 "Б" классе, а в 6 "А" на 17% (таблица 2).

Таблица 2. Уровни усвоения знаний у учащихся на конец эксперимента

Уровни усвоения знаний	Баллы	6 «Б» класс (количество учащихся)	6 «А» класс (количество учащихся)
Высокий	9- 10	2 (7%)	4 (13%)
Продвинутый	7 – 8	9 (32%)	15 (50%)
Средний	5-6	9(32%)	8 (27%)
Пониженный	3-4	8 (28%)	3(10%)
Низкий	0-2	0	0

Как видно из таблицы, средний уровень учащихся уменьшился в обоих классах, однако, следует иметь в виду, что значительная часть учащихся перешла на продвинутый уровень.

Таким образом, по результатам проведенных занятий с применением принципа укрупнения дидактических единиц можно сделать следующие выводы:

• V    одновременное изучение схожих тем позволяет улучшить усвоение учебного материала [5];

• V    применение принципа укрупнения дидактической единицы повышает качество усвоения учебного материала;

• V    применение принципа укрупнения дидактической единицы сокращает учебное время, которое можно использовать при повторении в конце четверти или учебного года.