Температурная зависимость удельной проводимости бислоя графена

Проблема создания наноструктур с заданными свойствами и контролируемыми размерами входит в число важнейших проблем XXI века. Ее решение революционизирует электронику, материаловедение, механику, химию, медицину и биологию. В последние годы интерес к наноструктурам и нанокластерным системам значительно возрос с точки зрения их применения в нано- и оптоэлектронике. В 2004 г. удалось экспериментально получить отдельные графеновые слои толщиной в один атом углерода [7–10]. Следовательно, возникла необходимость изучения различных свойств и характеристик данного материала. Графен интересен не только с точки зрения возможных приложений, но и с фундаментальной точки зрения – вследствие своих уникальных электронных свойств. Вблизи уровня Ферми электроны в графене обладают линейной дисперсией, а энергетическая щель между валентной зоной и зоной проводимости отсутствует. Модель зонной структуры графена послужила стартовой площадкой для изучения свойств графита, но в многослойных стопках, в частности в бислое, взаимодействие между слоями существенно искажает свойства графена [ibid.]. И только после 2004 г., когда отдельные слои графена были успешно изолированы, стало ясно, что на примере этой системы фактически можно изучать новый вид частиц – безмассовые заряженные квазичастицы, нигде больше не существующие в природе. Такие свойства этих частиц, как двумерность, спинорная природа, нулевая масса и отсутствие щели в спектре, приводят к ряду электронных явлений, не имеющих аналогов ни в каких других физических системах [8].

На основе бислоя графена возможно создание различных наноэлектромеханических систем, например нановесы, нанодиоды, нанотранзисторы. Одной из важнейших характеристик таких приборов является электропроводность [2; 6].

• 1.    Зонная структура и удельная проводимость

В настоящей работе рассматриваются четыре высокосимметричных случая расположения графеновых слоев друг относительно друга: без смещения (рис. 1а); со смещением в половину длины связи (б), так называемый графит Бернала; со смещением в длину связи (в) и ³/₂ длины связи (г). Для расчета зонной структуры бислоя графена необходимо знать интеграл перекрывания для волновых функций 2 p_z -орбиталей.

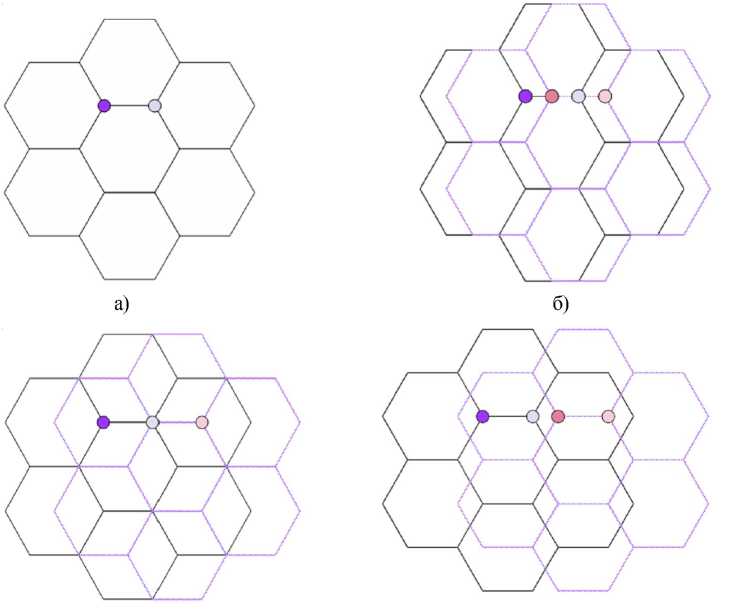
в)

г)

Рис. 1. Различные варианты расположения слоев друг относительно друга:

а) смещения по оси Y нет; б) смещение по оси Y на половину длины связи; в) смещение на длину связи; г) смещение на ³/₂ длины связи

Общий вид волновой функции для 2 p_z -орбитали в сферической системе координат:

Ч'  =

2 pz

4 2 π

}cos 0, здесь Z - порядковый номер углерода; а_в = 0.5292 a — пер- Zr

вый Боровский радиус; р =   - радиус-вектор. Зная волновую функцию, получим значения aB интеграла перекрывания для атомов углерода, принадлежащих разным слоям графена (см. таблицу).

Таблица

Значения интеграла перекрывания, d – расстояние между слоями графена, Δ – смещение одного слоя относительно другого

	0	«о / /2	л/Зао/ /2	^0
0,8*d	7.29* io"4	4.59*10"4	1.87*10 4	1.22*10^*
d	3.55* IO"3	2.41*105	1.14*105	7.94*10“
1.2*d	1.44*10 й	1.05*10“	5.56*10-’	4.O6*io"7

Для нахождения дисперсионных соотношений пользуемся методом МО ЛКАО, то есть волновую функцию записывают в виде детерминанта, построенного из одноэлектронных волновых функций. В кристаллах с трансляционной симметрией функции, зависящие только от координат электрона, называют блоховскими.

Для рассматриваемой системы базисные блоховские функции имеют следующий вид:

^ A ( r ) = -17 E exP^' ^{( kl} 1 c l + ^kl 2 c 2 ^)} P a ⁽ r — ¹ 1 c l — ¹ 2 c 2 )

L l 1 , l 2

^T B ⁽ r ) = "77 E ^еХР ^{{ ( k1} 1 c l + ^k1 2 c 2 ^)} P b ⁽ r — ¹ 1 c l — ¹ 2 c 2 )

L l 1 , l 2

^ C ⁽ r ) = At E ^eXP^{' ^{( k1}1 c l + ^kl 2 c 2 ^)} P c ⁽ r — d I — l l c l — ¹ 2 c 2

L l 1 , l 2

^T D ⁽ r ) = "77 E ^еХР ^{{( k1} 1 c l + ^k1 2 c 2 ^)} P d ⁽ r — d 2 — ¹ 1 c l — ¹ 2 c 2 )

L l 1 , l 2

Здесь p_A, p_B, p_C, p_D – атомные орбитали p -типа. В таком базисе, используя приближение ближайших соседей, определяем дисперсионные уравнения четвертого порядка для законов дисперсии п -электронов в четырех высокосимметричных случаях, которые описывают электронные переходы в бислое графена. Метод получения дисперсионных соотношений наглядно описан в [2].

Переходы вдоль слоев и между ними взаимосвязаны. Зонная структура бислоя графена наглядно изображена на рисунке 2. Для расчетов использовались следующие значения параметров: химический потенциал: ц ^а = ц ^с = 0 эВ; кулоновская энергия: U =10 эВ.

• а)                                          б)

Рис. 2. Зонная структура двойного графенового слоя:

• а)    по вертикальной оси отложена энергия, по горизонтальным – проекции волнового вектора k_x , k_y ;

• б)    вид сверху

На рисунке 2 видны «особые» точки энергетической поверхности, в которых энергия принимает экстремальные значения и имеет линейный характер (конусы). В конусах в приближении слабых возбуждений кристалла существуют безмассовые дираковские квазичастицы [8]. Поэтому двухслойный графен является перспективным материалом для создания современных устройств электроники.

Выражение для тензора удельной проводимости, полученное методом функций Грина [1], двухслойного графена в двухзонной модели Хаббарда [4; 5] имеет следующий вид [3]:

G_a p = i ^z e- EE v £ ( q ) v в ⁽ k ) A a + v a ( q ) v c ( k ) A _c + ^kT V q, X k, a

+ ⁽ v a ⁽ q ) v c ^{( k} ) + v a ⁽ q ) v a ^{( k} ) )

A_a + A_c En_ac i a c । ac

к

ch E 1 +1 к kT )

, ( E 1

sh

к kT ) )

где величины v _ap A

– компоненты групповых скоростей электронов в зоне Бриллюена;

– функции Грина операторов рождения и уничтожения электронов;

nac – количество переходов между слоями;

E – энергия электронов;

e ас - полученные дисперсионные соотношения для переходов между слоями.

Температурная зависимость электропроводности, рассчитанная по формуле (2), представлена на рисунке 3.

1,6

1,4

1,2

£ Е О го Е О) <У)

1,0

0,8

0,6

0,4

0,2

0,0

100       150       200

250       300

T,K

Рис. 3. Температурная зависимость электропроводности бислоя графена

Заключение

В заключении можно сделать следующие выводы:

• - Удельная проводимость двухслойного графена не зависит от выбранного направления в кристалле и носит металлический характер. Так как перпендикулярная составляющая волнового вектора k _± имеет непрерывный набор значений, то при любом выделенном направлении существуют точки, при которых проводящие и валентные зоны пересекаются (рис. 2а). Но следует отметить, что в случае ограничения пространства для движения электронов, тем-

• пературная зависимость проводимости может измениться и для некоторых направлений принять вид, характерный для полупроводниковых материалов.

  -Предсказана слабая зависимость проводимости от взаимного расположения слоев графена. Это связано с тем, что между слоями присутствует лишь слабое Ван-дер-ваальсовое взаимодействие, что приводит к малому значению интеграла перекрывания, а следовательно, и энергии перехода между слоями. Однако включение внешних полей может существенно увеличить параметры системы, и межслоевые электронные переходы будут намного больше влиять на различные физические свойства данной системы.

ПРИМЕЧАНИЕ

• ¹    Работа проведена в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы [проект № НК-16 (3)], а также поддержана грантом № 61-2010-а/ВолГУ.