Температурное поле однородной квадратной области с движущимися без ускорения смежными сторонами при граничных условиях первого рода

Введение. Интерес к задачам с движущимися границами не ослабевает в связи с многопредметными приложениями: идентификация движущейся границы для обратной задачи теплопроводности [1]; прогнозирование переходной свободной конвекции и тепловой стратификации в резервуарах хранения сжиженных газов в присутствии микропримесей [2, 3]; оценка термического воздействия на защитные ограждения [4]; изменение объема при тепловой обработке в пищевой технологии [5, 6]; повышение эффективности абляционной защиты гиперзвуковых обтекателей летательных аппаратов [7] и т. д. Если ограничиваться переносными характеристиками в практических применениях, то их математические модели формализуются на основе фундаментальных законов Фурье и Фика в виде уравнений в частных производных параболического типа либо их систем с соответствующим набором краевых условий, в том числе и на части или на всей границе, движущейся по произвольному закону с сохранением ее гладкости [8]. В частности, при описании задач с фазовыми переходами на движущейся границе (плавление или кристаллизация) [9] добавляется условие Стефана [10] и формулировка такой задачи переходит в классическую формулировку Стефана.

Рис. 1. Расчетная схема области

Только ограниченное число задач с движущимися границами допускает аналитическое решение, к которым относятся в основном классические одномерные задачи Стефана и Неймана [11], а также найденные в последнее время новые решения [12–15], но тоже в одномерной постановке.

В связи с этим актуален поиск новых решений задач для 2D-областей, в которых части границы движутся в разных направлениях.

Постановка задачи. Рассматривается однородная по теплофизическим характеристикам (коэффициент температуропроводности a - const) деформируемая с сохранением подобия область ABCO в декартовой системе координат (xOy), для которой AB - BC - CO - OA - h0 (рис. 1). В начальный момент времени т = 0 стороны AB и BC начинают двигаться соответственно в направлении осей абсцисс и ординат с постоянной скоростью u, оставаясь им параллельными, причем локальная температура в каждой точке области одинакова и равна t0 - const, при т > 0 сто рона AO и OC также поддерживается при температуре tо, а стороны AB и BC при t1 = const.

Изменение локальной температуры t ( x , у, т ) во внутренних точках рассматриваемой области должно быть определено из следующей начально-краевой задачи:

д t ( x , у , т )       д 2 t ( x , у , т )    д 2 t ( x , у , т ) = а     х        +    х         ;                              (1) дт           д x 2          д у 2 t ( x, у ,0 ) = t ( 0, у , т ) - t ( x ,0, т ) = 1 0 ;                                 (2) t ( h , у , т ) = t ( x , h , т ) = t 1 ;                                           (3)

h ⁽т) = h 0 - и т .                                         (4)

С помощью относительных переменных

0 - а ^ h 0 ; X - x(h 0 ; Y - y/ h ₀ ; T ( X , Y, 0 ) -[ t ( x , у, т ) - t ₀ ]/ ( t 1 - t ₀ ) ; A - uh₀ (a ; H (0)- 1 - A 0 система (1)–(4) записана в безразмерном виде:

at(x,y,0) _ д2 t(x,y,0)  дгт(x,y,0)

-               +                ;                           (5) д 0         д X 2          д Y 2 T ( X , Y ,0 ) - T ( 0, Y , 0 ) - T ( X ,0, 0 ) - 0;                          (6) T [ H ( 0 ) , Y , 0 ] - T [ X , H (0 ) , 0 ] - 1;                              (7) H ( 0 ) - 1 - A 0 .                                   (8)

Применение координат ( а , в , у ) [16]:

а - X/(1-A0); в - Y/(1 - A0); y - 0 иммобилизирует движущиеся стороны области и трансформирует систему (5)–(8) дО(а,в,Y) =_ A   дО(а,в,Y) ! дО(а,в,Y) + дY        1 - Ay _    да          дв    _ A    [д2О(а,в, Y)  д2О(а,в,Y) 1 +                                 +                    ,                                  (9) (1 - Ay)2 L    да2           дв2    J П(а, в,0)-^(0, в, Y )-^(а,0, y )-0,                        (10) Q(1, в, Y )-^(а,1, y )-1,                                 (11) где

^(а, в, у) = T [ X (а, в, у), Y (а, в, у ),0(а, в, Y )J •

Решение. Пусть

^ ( а , в , Y ) = q ( а , в , Y ) W ( а , в , Y ) ,                            (12)

где q = q(а,в,Y), W - W(а,в,Y) — функции, которые будут определены ниже. С помощью (12) уравнение (9) запишется в виде aw     1   a2w     1   a2w [  аА      1   2 aqIdw

-"+             + -;+                   + дY   (1 - Ay )2 да2  (1 - Ay )2 дв2  L 1 - Ay  (1 - Ay )2 q да J да

+	в A       1    2 д q "	д W  1 1	а А  д q      1     д 2 q 1 ---- +-----у- W +
	1 - a y  ( 1 - A y ) 2 q дв	д в   q	1 - A y да  ( 1 - A y ) 2 д а 2

1Г  вА dq      1    d2q q 1 - Ay дв  (1 — Ay )2 двв

Подстановка q ( а , в , y ) как координатный мультипликатор

W .

q ( а , в , y ) = q ( а , y ) q 2 ( в , y ) , где q₁ ( а , y ) , q ₂ ( в , Y ) идентифицируются соответственно из условий

—

аА  ,      1     2 д ъ           5 1.      1     2 д q 2

1 — A y  ( 1 — A y ) 2 q 1 да ’   1 — A y  ( 1 — A y ) ² q 2 дв    ’

откуда

q 1 ( а , y ) = C 1 ( Y ) exp

1 A а ² ( 1 — A y )

q 2 ( а , y ) = C 2 ( Y ) exp

1 Л в ² ( 1 — A y )

где константы интегрирования C1 ( у ) и C2 (Y) определяются из выполнения тождеств аA дq1 ,    1    д 2 q =0

1 — A y да ( 1 — A y ) ² да ²

в A д q 2 ₁      1 д q ,   ₍₎

1 — A y дв  ( 1 — A y ) ² дв ²

что обеспечивается, когда C ₁ ( y ) = C ₂ ( y ) = ( 1 — A y )^{/ 2} •

Таким образом соотношение (12) принимает структурированный вид

^ ( а , в , Y ) = W ^{( а} , ^в , ^Y ) exp 1 A ( 1 — A y )⁽ а ² + в 2 ) •

1 — A y      L 4                     _

С помощью (14) из системы (9)-(11) следует начально-краевая задача для W(а,в, Y): дW _    1   (д2W д2WЛ , дY "(1 — Ay)2 (да2 +дв2 J ;

W ( а , в ,0 ) = W ( а ,0, у ) = W ( 0, в , Y ) = 0;

W ( 1, в , Y ) = F 1 ( в , Y ) ,            W ( а ,1, y ) = F 2 ( а , Y ) ,

где

F 1 ( в , Y ) = ( 1 — A y ) exp

^— 1 A ^{( 1 —} A ^{Y ) ( 1 + в 2} )

F 2 ( а , Y ) = ( 1 — A y ) exp

— 1 A ( 1 — A y )( а ² + 1 )

Исходная функция W ( а , в , Y ) представлена как суперпозиция функций W ₁ ( а , в , Y ) и W 2 ( а , в , Y ) , т. е.

W (а, в, Y ) = W (а, в, Y) + W2 (а, в, Y),(18)

где W ₁ ( а , в , Y ) и W₂ ( а , в , Y ) являются решениями следующих начально-краевых задач:

д W 1 ( а , в , Y )_     1     Гд ² W 1 ( а , в , Y M W ( а , в , Y ) ]

+                   ,\ дY       (1 — Ay)2 L да2           дв2

W (а, в,0) = W (а,0, y ) = W1 (0, в, Y) = 0;(20)

W ( 1, в , Y ) = F 1 ( в , Y ) , W ( а ,1, Y ) = 0,                             (21)

д W 2 ( а , в , Y ) =     1	" д 2 W 2 ( а , в , Y ) , д 2 W 2 ( а , в , Y ) "	,                   (22)
д Y       ( 1 — A y ) 2	L    д а 2            д в 2     J
W 2 ( а , в ,0 ) = W 2 (	а ,0, y ) = W 2 ( 0, в , Y ) = 0;	(23)
W 2 ( 1, в , Y ) = 0,	W 1 ( а ,1, y ) = F 2 ( а , Y ) •	(24)

Для нахождения W 1 ( а , в , у ) вновь воспользуемся суперпозицией неизвестных функций

W (а, в, у) = V (а, в, у) + U1 (а, в, у),(25)

где U ₁ ( а , в , У ) представим как

U! (а,в,Y) = U* (а,в, у) W (1,в,Y),(26)

причем Uy (а,в,^) — lim Uj (а,в, Y), а U* (а,в, Y) есть решение вспомогательной задачи у ^да дU* (а,в, Y) = д2U* (а,в, Y) ! д2U* (а,в, Y)

ду     "    да2           дв2’

U * ( а , в ,0 ) — U * ( а ,0, у ) = U * ( 0, в , Y ) = U * ( а ,1, у ) = 0;

U * ( 1, в , Y ) — 1.

Поскольку решение (27)–(29)

U* (а, в, Y) = 2] '--csqk)[sh^ + 2]  "s"“) exp"У)1 sin („-в),(30)

Л=11   q-   Л shq-     м ("?+q-)cos"J где qk — nk, di — ni, k,i — 1,да, то при у ^ да из (30) следует

*/        х          1 - cosq, ^ sh(q, а)     ,,

U^, в, да) = 2]------- I—----sin (q^).

k = 1 1    q -    J ^sh q -

С помощью (25), (26) и (31) система (22)–(24) может быть представлена относительно

V 1 — V 1 ( а , в , у ) в виде:

2 А ₊ ^д^-и-АуА2 U ₊ дПх ₊ ' U.

+ ох1 Ау       +      + ду да2 дв2          ду   да2

V (а,в,0)=-U* (а,в,да)F1 (в,Y);(33)

V (а,0,у) — V1 (0,в,Y) = V (а,1,у) — V (1,в,Y) — 0 .(34)

Применение конечного интегрального синус-преобразования Фурье по переменной а к системе (32)–(34)

Ф 1 — Ф 1 ( а , A n , у ) — J V_x ( а , в , Y ) sin ( А п в ) d в ,

Py — Ру (а, Ап,у) —JU1 (а,в, Y)sin(Апв)dв , где An — пп, п — 1, да, переводит ее в систему а2 дФх   д2Фх               , \2 дР  д2Ру    2_

(1-AY)     — —"г- А2ф1 -(1-AY) ^г1 + —-- A2P;

д у д а ²                   д у д

Ф1 (а, Ап ,0) — -JU* (а,в,да)Fx (в,0)sin(Апв)dв ;(36)

Ф1 (а,0, у) — Ф1 (0, в, Y) — Ф1 (а,1, у) — Ф1 (1, в, Y) — 0.(37)

Применение конечного интегрального синус-преобразования Фурье по переменной в

^ 1 ^— ^ 1 ( М т , ^А п , Y ) ^— J ^ф 1 ( ^а , ^А п , у ) ^sin ( М т ^а ) ^{d а} ,

0 1

Q1 — Q1 (Мт, Ап, Y) — J P1 (а, Ап, Y)sin (Мта) dа к (35)-(37) генерирует задачу Коши относительно Т1

d T 1 + M m + A n T =_ d 9   ( 1 - A 9 ) 2  1 T ( M m , A n ,0 ) = - j j U * ( a , p , « 00

dQL + M m + A n Q d 9   ( 1 - A 9 ) 2 3) F 1 ( P ,0 ) sin ( A n P ) s

= L 1 ( 9 ) , in ( M m a ) d a d P ,

L 9 ) =- jj

d U1 + M^ U sin (AnP) sin (Mma) dad в ,

69   ( 1 - А в ) ^{2  1}

решение которой

^T 1 ( M m , ^ n ^{, 9} ) = exp

_ ^{( M m +An ) в} .

1 - A 9    I

T ( M m , A n ,0 ) + j L 1 ( 9 ) exp

^{( M m + A} „ ) ⁹

1    9 d ⁹

Оригинал (38)

V V

V 1 ( X , Y , 9 ) = 4 ^^ ^ 1 ( M m , A n

и в итоге

W ( — , Y, 9 ) = U * I —- , -Y- , V I F I - Y -, 9 | + V ( — , Y, 9 ) . ^1V       ’    ¹ 1 1 - A 0 1 - A 9   ) ¹ 1 1 - A 9  )   ^1V       ’

Решая систему (22)–(24) аналогичным образом, получим

W ( — , Y, 9 ) = U * | -X- ,- Y -, v | F | - X -, 9 | + V ( — , Y, 9 ) , ²        ’    ² 1 1 - A 9 1 - A 9  ) ² 1 1 - A 9  )    ²

где

R \ n УГ¹ - cos Pl A sh⁽ p^P ) ■ (    \         1

^U 2 ( ^a , ^в , ^V ) = ² У --------^L          sin( q k ^a ), P i = n l ;

l = 1 1     Pl     )  ^sh P l

V ( X , Y , 9 ) = 4 У У Ч', Mm , A , 9 sin I ^{M m}   I sin I    ''    I

22 mn

;

^T 2 ( M m , ^A n^{, 9} ) = exP

-

( Mrn ^{+ A}n ) ⁹

1 - A9   ‘

T ( M m , A n ,0 ) + j L 2 ( 9 ) exp

( M m ^{+ A} n ) ⁹

-----— d9

1 - A 9

;

^{T o} ( M m , ^A n ^,0 ) = ^- j j U 2 ( ^a , ^в , ^V ) F 2 ( ^{a ,0} )( M m ^a ) ^sin ( ^A n P ) ^{sin d a d} P ;

^L 2 ( ⁹ ) = - jj

^dUH      ( n A

—У = U 2 ^{( a} , ^P , ^v) o9

d U 2 ₊ Mm + An _TT

⁺        U

69   ( 1 - A 9 ) ²

- A + ¹ A ² ( 1 - A 9 ) (1 + a² 4

sin ( A _n P ) sin ( M _m a ) d a d p ;

) ^exP |^{- 1} [ ^{A a 2 ( 1 - A 9 ) + A ( 1 - A 9} ) ]

Таким образом, окончательное решение с учетом (14), (40), (41) таково:

T ( — , Y , 9 ) =

W 1 ( — , Y , 9 ) + W₂ ( — , Y , 9 ) 1 - A 9

A — ² + Y '²

4  1 -

Результаты расчетов по (42) показаны на рис. 2, которые при безусловном выполнении на- чального условия иллюстрируют справедливость полученного аналитического решения в квадратурах.

Заключение. Полученное решение может быть обобщено на случай A <  0, а также на движение частей границы области в разных направлениях и с разными скоростями. Кроме того, нет никаких ограничений к распространению изложенного подхода для равноускоренного или равнозамедленного движения сторон, а также при наличии источника или стока теплоты.

б

а

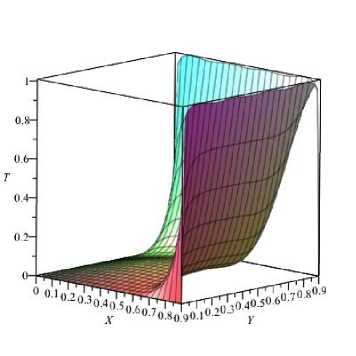
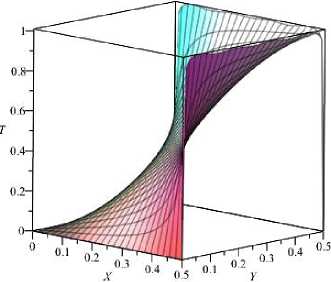
Рис. 2. Температурное поле при A = 1 и различных 6 : а - 0,1; б - 0,5

Авторы выражают искреннюю благодарность профессору А.В. Богомолову за участие в обсуждении выбора метода решения задачи и поздравляют его с юбилеем.