Температурное поле тепловыделяющей жидкости в квадратной области с неоднородными граничными условиями первого рода

В связи с проблемой хранения радиоактивных отходов пристальный интерес исследователей вызывает изучение поведения тепловыделяющих жидкостей в замкнутых объемах при различных граничных условиях на смоченной поверхности [1, 2]. Для решения этой задачи необходимо рассмотрение тепловой обстановки не только в турбулентном и ламинарном режимах, но и в кондуктивном, когда вязкость среды высока из-за присутствия твердой дисперсной фазы. Это дает основание использовать в качестве модельного представления о механизме переноса теплоты только молекулярную теплопроводность [3]. В такой постановке задачи можно идентифицировать структуру температурного поля и определить ряд характеристик, среди которых локализация и величина максимальной температуры имеет наиболее важное прикладное значение.

Рассматривается квадратная область со стороной h , м, содержащая теплопроводную среду с однородной мощностью тепловыделения q , Вт/м ³ , и известными теплофизическими характеристиками - плотностью р , кг/м ³ ; теплопроводностью X , Вт/(м - К); теплоемкостью c p , Дж/ (кг - К), одна сторона которой поддерживается при температуре t ₁ , К, а остальные – при температуре t ₀ , К. Математическая формулировка задачи в этом случае будет:

д t

P c p = ^X дт

д ² 1 д ² 1 ^д x ^{2 +} д у ² ,

+ q ;

t ( x , h ) = 1 1 ;                        (2)

t ( h , у ) = t ( x ,0 ) = t ( h , у ) = t o ;              (3)

где т - текущее время, с; t - локальная температура, К.

Пусть для определенности 1 1 >  1 ₀ , тогда система (1)–(3) в безразмерном виде такова:

дt = 1 [ д2 T + д2 T | + J_;

д9 Pr ^д X ^{2 +}д Y ² J⁺ Pr ;

T (X ,1) = Ti;(5)

T (0, Y ) = T (X ,o)= T (1, Y )= 0;

где X=x; Y=y;  9=TV; Ti = h         h h2

^{( t} i ^- t о ^{) х} .

qh ²     ;

V

Pr = —; v, a - кинематическая вязкость и a теплопроводность среды, м2/с.

Будем рассматривать стационарный случай, тогда система (4)–(6) трансформируется в систему

д ² T д ² T д X ^{2 +} д Y ²

T ( X ,i ) = T i ;                    (8)

T ( 0, Y ) = T ( X ,0 ) = T ( 1, Y ) = 0 . (9)

Данная задача является задачей Дирихле для эллиптического уравнения в прямоугольнике. Ее решение имеет вид [5]

Для двух методов решения получим следующие графические зависимости для x = 0.5. Исходя из рис.1 можно заключить, что решение, полученное при помощи конечных интегральных преобразований и методом разделения переменных, одинаково.

да

- 2

T 1 ( X , Y ) =          .

п =Ц sh ( Ц п )

да ^х sh ( u ^Y ) + Е т = 1

^T « ^{( COS} ^ - 1 ) 1 sh ( Р п У )

² ( cos Ц т - 1 )

3 ³

^Ц т

Ц п

ch ( Ц т Х ) + 1-^ х

Sh U n

х sh ( ц _тХ )} sin ( ц _mY ) + 0.5 Y - 0.5 Y ² .    (10)

Однако решение задачи (7) - (9) можно получить в другой форме, используя конечное интегральное преобразование.

Применим конечное интегральное синус-преобразование [4] по переменной X :

dy X - 22 Tx = 2(cos 2 - 1) ;(11)

Tx (0) = 0;

Tx (1) = -T- (cos 2 -1), где TX - изображение T; 2 - корни характеристического уравнения sin 2 = 0. Решение уравнения (11) с граничными условиями (12) -(13) имеет вид

T X

cos 2 - 1

shl2', Y>U ' -Jsh(2Y),

22       122     )

— sh22

0             0.5

y

Рис. 1. Сравнение профилей температур в средин -ном сечении области решения

Решение (15) может быть обощено для различных вариантов граничных условий

T ( 0, Y ) = T 1 ; T ( 1, Y ) = T ( X ,0 ) = T ( X ,1 ) = 0 ; (16) T ( 1, Y ) = T 1 ; T ( 0, Y ) = T ( X ,1 ) = T ( X ,0 ) = 0 ; (17) T ( X ,0 ) = T 1 ; T ( 0, Y ) = T ( X ,1 ) = T ( 1, Y ) = 0 ; (18) T ( 0, Y ) = T ( X ,1 ) = T 1 ; T ( 1, Y ) = T ( X ,0 ) = 0 ; (19) T ( 0, Y ) = T ( 1, Y ) = T 1 ; T ( X ,1 ) = T ( X ,0 ) = 0 ; (20) T ( 0, Y ) = T ( X ,0 ) = T ( 1, Y ) = T 1 ; T ( X ,1 ) = 0 . (21)

Для граничных условий (16)-(18) решения по структуре аналогичны (15), а для граничных условий (19)-(21) решения получены с использованием принципа суперпозиции в силу линейности задачи:

Используя формулу обращения интегрального синус-преобразования [4], получим

_T = ₂ ^^ cos Ц т ^{- 1} т = 1    ^Ц т

sh h ^ m X !

Ц _т

^T 1      2 I sh ^{[ ц} т ^{( 1 - X} ) ]

^Ц т )

—

sh u

m

” cos 2 - 1

T = 2Х----

„=1     2 -

sh [ 2 - ( 1 - Y )] + 2-²

V

1           )           .

- T 1 sh ( 2 - Y )

.²- ²       )

sh [ 2 п ( 1 - Y )]

-

—

2п2

где 2 _п = п п , п = 1, да .

sh 2 _n

Ц т

Sin ( Ц m Y ) + 2 ] T ^ 2 _1 п = 1     ² п

2 п ²

sh 2 _n

—

sinC ^ X ) ,

T ,-^ sh ( 2 n Y )

V ² п )             ¹

— ^{sh 2} n           2 _п ²

^{[ sin ( 2} n^X ) ;

T = 2 J cos ^ m ^{— 1}

m = 1    Ц

m

T = 2 £ COs ^ m ^— 1 m = 1    P m

m m

^sh Vm ( 1 ^— X ^{) ]}

2 ^ m

P m

I 2            1

+ 1 --- 2 ^— T i I sh ⁽ ^ m X )

V ^ m     у

^sh ^ m

sin C^ y ) ;

sh \m™(1—X)]

2 P m

I 2                I

+ 1 --- 2 ^— T I sh [ m m ^{X ]}

V ^m m     у

sh m

m

Г sh ( ^ n y )

—

sinC^ y ) + 2 :£ ^ n-^ n = 1 ^ n

A n 2

sh A n

—

T 1 — TT sh [ A n ( 1 — У )]

V A n ² J                   1

— shAn            An2

[ sin ( A n X ) , (24)

где Au m - корни уравнений sin A = 0 и sin m = 0 .

Структура температурных полей при различных граничных условиях показана на рис. 2. Видно, что увеличение T ₁ приводит к пропорционально-эквидистантному увеличению значений температур в области решения.

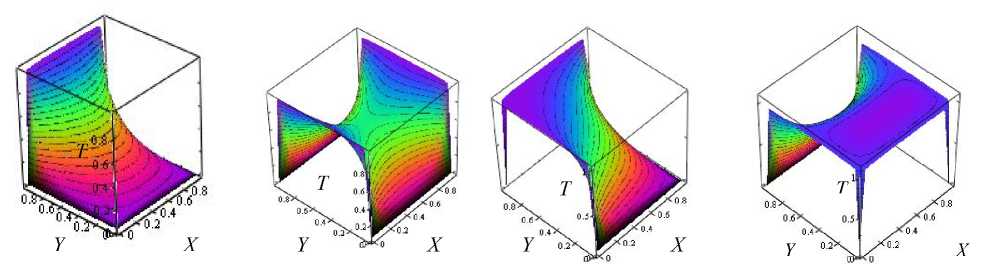
Рис. 2. Температурные поля при T 1 = 1 , соответствующие решениям (15), (22)-(24)

Анализ рядов, проведенный численно, позволяет сделать вывод о быстрой их сходимости. Hапример, представленные температурные поля на рис. 2, получены при n = 25, что вполне по точности удовлетворяет инженерной практике. Отметим, что в случае нагрева противоположных сторон, температурное поле имеет структуру “седла”. Таким образом, неоднородность температурного поля определяется неоднородностью граничных условий, которую необходимо учитывать в задачах переноса теплоты в тепловыводящих жидкостях в кондуктивном режиме.