Temporal Logics Specifications for Debit and Credit Transactions

Published Online April 2015 in MECS

In recent times, temporal logic stands out as one of the tools that is useful to specify and reason about concurrent and reactive systems because it provides a natural way to describe the temporal behavior of these kinds of systems [1]. It is possible to represent the systems and their properties by using temporal logics formulae. Also, we can express the implementations and specifications of the system as two formulae written using temporal logics, and then, verify whether the implementations imply the specifications. Modern operating systems and most of DBMS's extensively make use of concurrent algorithms [2], [3]. Hence, the correctness of these algorithms is very important to achieve system reliability. Now, the wide use of mobile and banking technologies has led to a huge number of concurrent users, may be, processing their database transactions simultaneously. In this case, infinite histories will be produced. The importance of representing such infinite histories has been considered [4], [5] and [6]. Usually, database techniques deal with a finite number of transactions concurrently executing [7] and [8].

Our research issue, in this paper, is to specify an infinite history of the debit and credit transactions in term of serializability, as a correctness criterion, using temporal logics formulae. The availability of model checkers gives importance to the temporal logics specifications. In this context, model checkers can carry out exhaustive checks for a correctness criterion of concurrent debit and credit transactions automatically with no need to the expertise in carrying out the verification [9] and [10].

Some researchers, in general, have taken into their accounts representing infinite histories in temporal logics [11] and [12]. And, they presumed that the serailizabiity is the correctness condition. In this research, we will introduce a computationally efficient condition of serializability that can be used to specify the correctness of concurrent transactions in temporal logics such as CTL and LTL. The serializability condition is relaxed in a way that keeps database in a consistent state. This condition is based on the nature of debit and credit transactions.

This paper is organized as follows. In Section II, we shall discuss the debit and credit transactions, conflict serializability condition and the relaxed condition of serializability. The syntaxes and the semantics of LTL and CTL are introduced in Section III . In Section IV, the properties of transition structure for read and write operations and their interpretations on LTL and CTL paths are depicted. Furthermore, The encoding of debit and credit transactions into LTL and CTL and the relaxed serializability condition are also given in Section IV. The conclusions are drawn in Section V.

• II.    Debit and Credit Transactions Model

• A.    Debit and Credit Transactions Model

In general, transaction is a collection of one or more operations on one or more databases. Formally as in [9], [4], [11] and [12], a transaction is a sequence of read/write operations partially ordered such that:

Definition 1 :

a debit or credit transaction T , accesses a set of data items Di = {x1, x2,., xk} ^ D , is a sequence of (totally ordered) of read and write operations, where every read operation r(x) precedes write operation w. (x), Vx.x E D., such that

Ti = ri (X1) w(X1)—ri (xk) w(xk).

As in [11],[9] and [13], a set of debit and credit transactions is denoted by T = T : i = 1,2,..} . A history h is an interleaving sequence of read and write operations belonging to different transactions in T . Hence, a transaction T E T participating, in a history h , is a subsequence of operations where every read and write operations occurring in a history h in the same order as they do in T . We shall denote to the operation o (where o is a read or write operation in a transaction T ) occurs in a history h before operation o _' by Ot г ' . In this paper, we assume that history h is considered to be serializable or correct (preserve the database in a consistence state) if it is equivalent to a serial execution of all transactions in T [14]. We formally define that two histories are equivalent as follows:

Definition 2 :

Histories h and h₂ of T = { T. : i = 1,2,.. } are equivalent, written as h ~ h , iff for all i , i ₂ >  1, i ^ i₂, and for all x E D ,

• 1    If r (x)

  3)    If wix(x)

We say that the history h is serializable if h is equivalent to a serial history h , as in the next definition.

Definition 3 :

A history h of T = { T : i = 1,2,.. } is serializable iff there is a serial history h of T of the form, for each i = 1,2,.. ,

hS  =     .„ricx)^wicy)^

only (all) steps of Ti such that h~ h.

• B.    Conflict graph and serilizability

Conflict graph is a directed graph that is built and used to test whether a history h , of the concurrent transactions, is serializable, and subsequently is a correct history. We consider that the history h is serializable if there is no cycle in the corresponding conflict graph. The importance of this graph is that the test of serializability can be done in a polynomial time [14]. We shall consider that two operations are conflicting, if belonging to different transactions, accessing the same data item and one of them is a write operation. Next, we shall define how we can build a conflict graph of concurrent transactions participating in a history h .

Definition 4 :

For each history h , there is a directed graph CG ( h ) called the conflict graph of h . t his graph has the transactions of h as its nodes, and contains an arc ( T , T ) , where T and T are distinct transactions of i ₁ i ₂                              i ₁                 i ₂

h , whenever there is a operation of T which conflicts with a subsequent (in h ) operation of T .

• C.    Serilizability of Debit and Credit Transactions

Usually, bank customers are interacting with bank database by invoking debit and credit transactions. Debit and credit transactions are representing the deposit and withdrawal to and from current balance of a bank account [15]. So, to understand the serializabiity of debit and credit transactions that are concurrently executing in a database, we shall give the following example:

Suppose that we have two data items x and y which are representing two bank accounts in a bank database, two transactions such that:

T : r1(x); x = x -100; W1(x); r1(y); y = y +) 100;w1(y)

T2: r2 (y); y = y — 200; w2 (y); r2 (x); x = x +200; w(x)

and assume that the concurrent execution of the transactions as follows:

h = r(x) w,(x) r2(y) w2(y) r1(y) w1(y) r2(x) w2(x).

Now, suppose the initial value of x is 1000 ( x = 1000 ) and the initial value of y is 500 (y = 500). After execution above the history h , the final values of x and y are 1100and 400 , respectively. But, the serializable execution of the two transactions T and T is such that:

hs = r1 (x) w1(x) r1(y) w1 (y ) r2 (y) w2 (y) r2 (x) W2 (x )•

Suppose that we have that the same initial values for x and y ( x = 1000, y = 500 ), then the final values of x and y , after execution of the history h , are 1100 and 400 , respectively. t his means that the final values of the concurrent transactions in the history h is correct.

But, according to the Definition 2 and Definition 3 , h is not seilaizable because it is not equivalent to the serial history h ( hh ) and does not leave the database in a consistent state. Moreover, if we build the conflict graph that is corresponding to the history h as in Fig. 1, then we notice that the graph contains a cycle. This means that the history h is not serializable and subsequently it is not a correct history.

• T1                       ♦Та

У

Fig. 1. Conflict graph of the history h .

Now, the above demonstration shows that the history h is not serializable but, at the same time, it is correct. The reason is that the addition and subtraction operations that are applied on debit and credit transactions are commutative and can be applied in any order [15]. This means that the condition of serializability in Definition 2 and Definition 3 is too restrictive. So, the relaxed condition of serializability of debit and credit transactions is defined formally as follows:

Definition 5 :

A history hr of debit and credit transactions T = T : i = 1,2,..} is serializable iff, for any transaction T E T and data item x E D , the read and write ( r ( x ) and w ( x ) ) are occurring in the history hr without interleaving with any other operation(s) from different transactions T E T of the same data item x . This will be of the form, for each i = 1,2,..

hr =  ... r (x) ... w. (x) ...

no r_j ( x ) or w_j ( x )

To demonstrate the above definition, consider the transactions that are in the above example such that

T : r (x); x = x -100; w (x); r1 (y); y = y +) 100;w1(y)

T>: r2 (y); y = y - 200; W2 (y); r2 (x);x = x+200; w(x)

and the following history

hd = rl(x)r2 (y)W2 (y)w1(x)rl(y)W1(y)r2 (x)w2 (x).

Now, suppose that we have that the same initial values for x and y ( x = 1000, y = 500) as in the above example, then the final values of x and y , after execution of the history h , are 1100 and 400 , respectively. This means that the final values of the concurrent transactions in the history h are correct. Moreover, the Definition 5 allows the operations from different transactions which are accessing different data items to be interleaved. This will relax the serializability condition in Definition 2 and Definition 3 to a new one which can be encoded into temporal logics in an easier way as we shall see later in this paper.

• D.    Infinite History of Debit and Credit Transactions

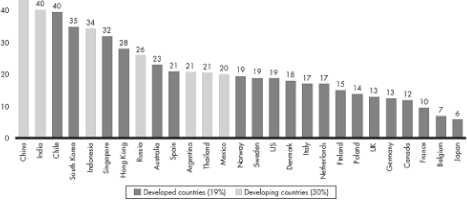
  For the last decade, most people around the world have had smart mobile phones. Accordingly, a huge number of people access the Internet for shopping. Bank transactions involve deposit and withdraw to/form bank accounts. These are called debit and credit transactions. In 2015, the expectations say that over 900 million people are expected to transact $1 trillion in the global mobile market [16]. So, we can expect that the number of debit and credit transactions is huge and the transactions are non-stopping. This means that millions of people are constantly depositing and withdrawing to/from bank accounts. Also, the statistics show that the use of mobile transactions for debit and credit in the developing countries has excessively increased, see Fig. 2. Such situation will produce infinite histories of debit and credit transactions.

Most database management systems consider that the histories are finite but such applications signify the need to deal with infinite histories [17]. One of the most techniques that can deal with modeling of infinite and finite behavior is temporal logics [18]. These histories will be encoded in temporal logics formulae as we will see in the next sections.

Percenloge 4 respo'dKh who uied smorlphooe/tiblef to male payments in the lost quarter 50% ⁴⁹

Source: Bain/Research Now and Bain/ GMI NPS Surveys, 2013.

Fig. 2 Mobile Payment in 2013.

• III.    Temporal Logics

In this section, we will introduce two famous types of temporal logics: Linear-Time Temporal Logic (LTL) and Computational Tree Logic (CTL).

• A.    LTL Syntax and Semantics

LTL is a logic that can be used to specify infinite histories composed of n transactions repeating infinitely many times. The compilation of all the iterations of the n transactions gives an infinite number of transactions T = {T : i = 1,2,..} . The reason for using LTL as a specification language is that the LTL formulae can be interpreted over infinite sequence of states which are useful for the histories that are produced in this context [19], [20]. Furthermore, LTL is accepted as a specification language in modern model checkers such as NuSMV.

• B.    Syntax of LTL

The alphabet of LTL consists of a set of propositions symbols p , i = 0,1,2, … , read/write step propositional symbols r ( x ), w ( x ) , where i ≥ 1 and 1 ≤ j ≤ | D | , boolean operations , ∨ , ∧ , т, ⊥ , and temporal operators X , F , G , U . f ormulae in ltl are of the form:

φ :: = p_i | r_i ( x_j )| w_i ( x_j )| φ | φ ₁ ∨ φ ₂ | φ ₁ ∧ φ ₂ | X φ | F φ | G φ | φ U φ .

The symbols ⊥ and т denote the truth values false and true respectively and the abbreviations ⇒ and ⇔ will denote usual implication and equivalency in logic, respectively.

• C.    Semantics of LTL

An interpretation for LTL , I(s), at a given state s∈ S, where S is a set of states, assigns truth values pI(si), r(x)I(si) and w(x)I(si) ( ∈{⊥,т } ) to propositional symbol p ,  r(x) and w(x), respectively. The model M , of the system to be specified, is represented by a structure of transition system called kripke structure see [4]. The semantics of a LTL formula φ is interpreted by the truth relation M,s 1= φ which means that φ holds at state s in the model structure M . If φ is a path formula, M,πφ means that φ holds along path π in the Kripke structure M . The relation 1= is defined as follows:

M , s p iff p ^{I ( si )} =т

M , s_i к r ( x ) iff r ( x ) ^{I ( si )} =Т

M , s_i к w ( x ) iff w ( x ) ^{I ( si )} =Т

M , s_i 1= φ iff M , s φ

M , s_i 1= φ ∨ φ iff M , s 1= φ or M , s и φ

M , s_i 1= φ ∧ φ iff M , s 1= φ and M , s 1= φ

M , s_i 1= X φ iff M , s 1= φ

M, si 1=Fφ iff there exists k≥ i such M,sk  φ that

M , s_i 1=G φ iff for all k ≥ i such that M , s и φ

M , s_i 1= φ U φ iff there exists c ≥ i , M , s и φ and, for all i ≤ b < c , M , s 1= φ .

• D.    CTL syntax and semantics

Actually, LTL and CTL formulae are different in their interpretations. Therefore, some formulae in LTL cannot be specified in the CTL formulae and vice versa. LTL formula is considering each path isolated. Hence, if each individual path holds the path formula, then LTL formula is true. But, To interpret a CTL formula, we consider the alternative possibilities for each state in a path.

• E.    CTL syntax

As in Subsection b , the alphabet of CTL consists of a set of propositions symbol p , p , … , read/write step propositional symbols r ( x ), w ( x ) (1 ≥ 1,1 ≤ j ≤ | D |) , boolean operations , ∨ , ∧ , Т, ⊥ , quantifiers E , A , temporal operators X , F , G and U . Formulae in CTL are generated by:

φ :: = p_i | r_i ( x_j )| w_i ( x_j )| φ | φ ₁ ∨ φ ₂ | φ ₁ ∧ φ ₂ | AX φ

EX φ | AF φ | EF φ | AG φ | EG φ | A [ φ U φ ] E [ φ 1 U φ 2 ].

In this logic, r ( x ) and w ( x ) are propositions but not predicates. The symbols ⊥ , Т , ⇒ and ⇔ have the same logical meaning as in Subsection B .

• F.    Semantics of CTL

In this subsection, we shall use the same interpretation function I ( s ) with the same meaning which has been introduced in Subsection C . in addition, the set of paths starting in a state s is denoted Paths ( s ) with Paths ( s ) ≠ {} . Therefore, the relation 1= is defined inductively as follows:

M , s p iff p ^{I ( si )} = т.

M , s_i ^r_i ( x_j ) iff r_i ( x_j ) ^{I ( si )}=т .

M , s_i и w ( x ) iff w ( x ) ^{I ( si )}=т .

M , s_i   φ iff M , s φ .

M , s_i   φ ∨ φ iff M , s к φ or M , s к φ .

M , s_i   φ ∧ φ iff M , s к φ and M , s ^φ .

M , s_i  AX φ        iff,         for         all

π∈ Paths(s ), M,s φ

M , s i 1=EX φ iff there exists π ∈ Paths ( s ) such that M , s  1= φ .

M , s i 1=AF φ iff, for all π ∈ Paths ( s ) , there exists b ≥ i such that M , s 1= φ .

M , s иEF φ iff there exists π ∈ Paths ( s ) and b ≥ i such that M , s 1= φ .

M,si 1=AGφ iff , for all π∈ Paths(s ), and, for all, b ≥ i,M ,s иφ .

M , s_i 1=EG φ iff there exists π ∈ Paths ( s ) such that, for all b ≥ i , M , s и φ .

M , s_i 1=A[ φ U φ ] iff, for all π ∈ Paths ( s ) , there is some c ≥ i such that M , s 1= φ and, for all a ≤ b < c , M , s и φ .

M, si 1=E[φUφ] iff there exists π∈ Paths(s ) such that, for some c ≥ i,M ,s 1= φ and, for all i ≤b

• IV.    Encoding Debit and Credit transactions into LTL and CTL

In this section, we shall give transition structure that has, at each state, a set of propositions which are either true or false. Therefore, as in [4], the set of propositions for each debit and credit transaction should satisfy the following properties:

• (C1) Write implies read

A transaction T can only be written to x if it has read x , i.e. if w(x) executes, thenr(x) must have been executed before.

• (C2) Read / write step proposition remains true until the transaction ends

If a read/write step has taken place, the corresponding proposition remains true until the transaction ends, i.e. r(x )/w (x ) is true, remains true until all operations belonging to the same transactions become true.

• (C3) At most one step occurs at each successive state

No two or more distinct steps can be false in a state, and then become true in a next state.

• (C4) Each read operation r(x ) should precede a write operation w (x ) without existence of any other read / write operation separate them.

This property emphasizes that the transaction of the form

T_i =r_i(x₁)w_i(x₁)…r_i(x_k)w_i(x_k)

as in Definition 1.

The semantics of the temporal formula (in CTL or LTL) φ is given by a truth relation M, s 1= φ , where M is a structure that satisfies the additional conditions (C1)-(C4). Therefore, given a state s , and a path π∈ Paths(s ), there corresponds a sequence of read and write step propositions that become true in s,s ,…. In this way, π yields a history of infinitely many occurrences (iterations) of the transactions T,…,T which are composing T ={T :i =1,2,..} .

We illustrate this correspondence between paths and histories by the following example:

Assume that we have the set of data items D = {x, y} and the debit and credit transactions are

T1 = r1(x)w1(x)r1(y)w1(y) andT2 = r2(y)w2(y)r2(x)w2(x).

The truth and the falsity for each read and write step propositions are given for successive states, and the top of each column, in Fig. 3, represents the unique proposition that becomes true in that state. The corresponding history h is:

h = r1(x)r2(y)w2(y)w1(x)r1(y)w1(y)r2(x)w2(x).

r1(x) s0 •	r2(y) s1 •	w2(y) s2 •	w1(x) s3 •	r1(y) s4 •
r1(x)	r1(x)	r1(x)	r1(x)	r1(x)
w1(x)	w1(x)	w1(x)	w1(x)	w1(x)
r1(y)	r1(y)	r1(y)	r1(y)	r1(y)
w1(y)	w1(y)	w1(y)	w1(y)	w1(y)
r2(y)	r2(y)	r2(y)	r2(y)	r2(y)
w2(y)	w2(y)	w2(y)	w2(y)	w2(y)
r2(x)	r2(x)	r2(x)	r2(x)	r2(x)
w2(x)	w2(x)	w2(x)	w2(x)	w2(x)
w1(y)	r2(x)		w2(x)
s5	s6		s7	…∞
• r1(x)	• r1(x)		• r1(x)
w1(x)	w1(x)		w1(x)
r1(y)	r1(y)		r1(y)
w1(y)	w1(y)		w1(y)	…∞

r2(y)	r2(y)	r2(y)
w2(y)	w2(y)	w2(y)
r2(x)	r2(x)	r2(x)
w2(x)	w2(x)	w2(x)

Fig. 3. The correspondence between path and history

• A. CTL and LTL Specifications

Now, the transactions model properties (or conditions) (C1)-(C4) can be encoded as follows

(C1) Write implies read

A transaction T can only be written to x if it has read x , i.e. if w(x) executes, then r(x) must have been executed before.

• 1.    CTL specification is:

σ₁= ∧∧AG(w_i(x_j) ⇒r_i(x_j))      (1)

• 1≤i≤n 1≤j≤m

• 2.    LTL specification is:

σ₁′ =∧∧G(w_i(x_j)⇒r_i(x_j))        (2)

• 1≤i≤n 1≤ j≤m

We shall add an extra proposition called end to indicate that the occurrence of T ends. This can be specified in CTL as follows

σ₀= ∧AG(end_i ⇔ ∧(r_i(x_j) ∧w_i(x_j))) (3)

1≤i≤n                    1≤ j≤m also, σ can be substituted in LTL by

σ₀′ = ∧G(end_i ⇔ ∧(r_i(x_j)∧w_i(x_j)))  (4)

• 1≤i≤n                  1≤ j≤m

(C2) Read / write step proposition remains true until the transaction ends

If a read/write step has taken place, the corresponding proposition remains true until the transaction ends, i.e. r(x )/ w (x ) is true, remains true until all operations belonging to the same transactions become true.

• 1.    CTL specification is:

σ = ∧AG((r(x ) ∧ end ⇒ AXr(x )) 1≤i≤n 1≤ j≤m

• ∧ (w (x ) ∧ end ⇒ AXw (x )))

• 2.    LTL specification is:

σ′ = ∧G((r (x ) ∧ end ⇒ Xr(x )) 1≤i≤n 1≤ j≤m

∧ (w (x ) ∧ end ⇒ Xw (x )))

(C3) At most one step occurs at each successive state

No two or more distinct steps can be false in a state, and then become true in a next state.

• 1.    CTL specification is:

σ₃= ∧ AG[((r_i(x_j) ∧r_i′(x_j′))

• 1≤i,i′≤n

• 1≤j , j′≤m i≠i′ or j ≠j′

• 2.    LTL specification is:

∧ EX(r(x )∧r_′(x_′)))∧

((r_i(x_j) ∧ w_i′(x_j′)) ∧

EX(r (x ) ∧w (x ))) ∧

((w_i(x_j) ∧ w_i′(x_j′)) ∧

EX(w_i(x_j)∧w_i′(x_j′)))].                    (7)

In the CTL specification in (7) we use the operators AGEX . Likewise, there is no LTL specification that is equivalent to the CTL specification. So, we can say that, there are properties that can be expressed in CTL but cannot be expressed in LTL and vice versa.

(C4) Each read operation r(x ) should precede a write operation w (x ) without existence of any other read / write operation separate them.

• 1.    CTL specification is:

• 2.    LTL specification is:

σ₄= ∧∧EF(r_i(x_j)∧r_i(x_j′)∧w_i(x_j) 1≤i≤n 1≤ j≠j′≤m                                                 (8)

∧w_i(x_j′))

σ₄′ = ∧∧F(r_i(x_j)∧r_i(x_j′)∧w_i(x_j) 1≤i≤n 1≤ j≠ j′≤m                                                (9)

∧w(x_′)).

Now, to make sure that all read and write operations do not become true after the transaction T ends, we shall add the following specification:

σ = ∧AG(end ⇒ AX(∧(r (x ) ∧w (x )) 1≤i≤n                         1≤ j≤m                              (10)

∧ end )).

or

σ₅′ = ∧G(end_i⇒X(∧(r_i(x_j)∧w_i(x_j)) 1≤i≤n                   1≤ j≤m                             (11)

∧end )).

We denote by σ (as in (12)) the specification that the transition structure of the histories (of debit and credit transactions) should satisfy. i.e

σdct =(σ0∨σ0′)∧(σ1∨σ1′)∧(σ2∨σ2′) ∧σ ∧ (σ ∨σ′) ∧ (σ ∨σ′).

Next, we shall encode the relaxed condition of serializability for Debit and Credit transaction (see

Definition 5)

σrcs =∧∧∧AG(ri(xk)∧rj(xk)

1≤i≤n 1≤ j≠i≤n1≤k≤m

⇒(wi(xk)∨wj(xk))).

• B.    CTL Specifications Vs LTL Specifications

In specifying the property C3 , we have seen that this property can be specified in CTL but cannot be specified in LTL. This could lead to a question: is CTL has more expressiveness power than LTL? the answer is no. To demonstrate this, we shall give a property to the system which can be expressed in LTL but cannot be expressed in CTL. For example: assume that we add a new property to the model such that

Every transaction started infinitely often is ended infinitely often

∧GFr (x )⇒ GFend .             (14)

1≤i≤n

This means that the transaction that becomes started infinitely often (and may become ended) must occur infinitely often. This kind of properties is called fairness property. Furthermore, if we need to ensure that every transaction is executed infinitely often such that:

∧FG end .                     (15)

1≤i≤n

This property can be only specified in LTL.

V. Conclusion

In this research paper, We have given an LTL and CTL specifications for debit and credit transactions. These specifications can be used to verify a scheduler uses to schedule an unlimited number of debit and credit transactions that incoming and outgoing from a bank database system. we have assumed that the serializability is the correctness criterion for concurrent debit and credit transactions executing in a transactional processing system. We have shown that the transactional system and its properties can be specified and encoded using temporal logics. Also, in this paper, we have introduced a transition structure to model the transactional system and its properties in terms of propositions. This propositions represent the read and write operations from different transactions that become true (executed) at this state. The verification part can be executed by model checkers, such as NuSMV, to test whether the database scheduler satisfies the relaxed serializability condition and its properties or not. In case of no, counterexamples to show the errors are automatically given by the model checker.

We have found that temporal logics (LTL and CTL) are suitable to specify the relaxed serilaizablity condition. Actually, we encoded the (infinite or finite) histories of the debit and credit transactions in terms of read and write propositions in the transition structure that we defined. This means that we can prove that the histories, produced by the concurrent execution of debit and credit transactions in a scheduler, are serializable if

σdct ⇒ σrcs. (16)

is satisfied. σ represents the temporal logic formula that specifies the behavior of the history in transition structure, that we have given above, and σ represents the temporal logic formula that specifies the relaxed serializability condition. This approach gives a fully automatic verification method that can overcome the disadvantages of the traditional approaches such as the user should understand in detail why the system works correctly (deductive verification), human error (mathematical proofs) and may not cover all possible system behaviors as in the simulation [21].

Acknowledgment

This research is funded by the Deanship of Research and Graduate Studies in Zarqa University /Jordan. Moreover, We would like to thank all members of faculty of information Technology and science at Zarqa university for their support to make these results possible.