Теорема о представлении меры

Сначала вводим некоторые определения и результаты из теории интеграла и меры. Пусть в ^ о определена вещественная борелевская мера ц , Е с ^ 0 — борелевское множество. Ограничением(сужением) меры ц на множество E называется мера ц_Е , которая определяется формулой ц_Е ( A ) = ц ( A D E ) для любого борелевского множества Л с М ^ .

Если ц_Е = ц , то говорим, что мера ц сосредоточена на множестве E .

Носителем меры ц (обозначение supp ц ) называется наименьшее замкнутое множество, на котором сосредоточена мера.

Меры ц и ц называются взаимно сингулярным, если они сосредоточены на непересекающихся борелевских множествах E и E .

Сформулируем следующие известные теоремы,

Теорема Жордана. Всякая вещественная мера однозначно представляется в виде ц = ц - ц, где ц и ц_ - взаимно сингулярные положительные меры.

Мера ц называется положительной составляющей меры ц .

Мера ц называется отрицательной составляющей меры ц .

Теорема Хана. Для любой вещественной меры ц в области G существует разложение G на два непересекающихся множества G и G , причем ц (E ) >  0 при Е с G_x ; ц ( E ) <  0 при Е с G ₂ .Хотя разложение G = G U G₂

не единственно, но меры ц и ц определяемые формулами ц ( E ) = ц ( E П G ) , ц ( E ) = ц ( E П G ₂) не зависят от выбора G и G ₂.

Из этих теорем следует, что если ц - вещественная борелевская мера на R Q , то существует борелевские множества Е_х и Е ₂ такие, что 1) К П = E i U E 2 ,   2) Е 1 П Е 2 =0 ,  3) ц + = Це_х , ц - = ^ .

Две меры ц , у е M, называются эквивалентными, если выполняется равенство ц ( Е ) = v ( Е ) для любых борелевских множеств Е , указанного выше вида.

Теорема.  Всякий элемент це M, эквивалентен разности ц - ц, где где ц и ц - положительные взаимно сингулярные локально конечные борелевские меры на RQ • Причем ц и ц определяются однозначно.

Доказательство.

Вначале докажем однозначность. Пусть существует ц , ц , ц , ц такие, что ц - ц = ц - ц , где ц и ц - положительные взаимно сингулярные меры, также как ц и ц . Пусть К с R Q - произвольный компакт, а ~, ц₂, ц₃, ц - ограничения мер ц , ц , ц , ц на компакт К . Имеем ц - ц = ц - ц . Пусть А_х и А₂ такие множества, что А П А = 0 , А U А = □ ” , мера ц сосредоточена на Л_х , а мера ц сосредоточена на Л ₂.

Пусть Е с Л_х . Тогда Д( Е ) + ц ( Е ) = ц ( Е ) , ц ( Е ) <  ц ( Е ) . Если Е с А , то о = Д ( Е ) < ц ~₃ ( Е ) . Из этого следует, что цц <  / ~₃ . Аналогично получаем 'ц_х >  ц ~₃ . Поэтому ц~_х = / ~₃. Отсюда следует, что ц = ц , а следовательно, и ц = ц . Однозначность доказана.

Теперь докажем первое утверждение теоремы. По условию ц = v -V, где v ,V - вещественные локально конечные борелевские меры на RQ. Пусть Ym =V,m-V2,т, m = 2,3,..., где V1,m,V2,m - ограничения мер v1 ,v2 на компакт   в(0, m) \ с' 0,— |. Отметим, что если k < m, то мера ук  есть

V m )

ограничение меры у_т на   в ( о, k ) \ C ' 0,1 | . Пусть R = А^m ) U A^m )

V k )

есть разложение Хана для меры Y_m . Тогда при k <  m имеем

Y k m ) ]( E ) = Y k ( e A A ⁽ m ) ) = Y ^f E A A m А в ( 0, k ) \ C ' 0,1 )) >  0 . V                  v ^k))

Аналогично y_k ,m , <  0 . Поэтому (3.1) есть также разложение Хана для меры

A 2

у_к . Далее находим, что

Х) ) +

\

V

в ( 0, k ) \ с ' 0,1

V k

( E ) = Y m ⁽ E A A( m ) А в ( 0, k ) \ C (0, k ) ) = Y k E А A^m ) ) = (y_k )₊ ( E ) . )

Это означает, что ограничение меры ( y m )₊ на в ( 0, k ) \ C 1 0, 1 I есть ( у )₊ .

V k J

Пусть теперь E <=D 0 - произвольное борелевское множество. Из (2)

следует, что при k <  m выполняется неравенство ( у )₊( E ) > ( у )₊( E ) . Таким образом, последовательность (у_т )₊( E ) возрастает, также как и последовательность ( у ) ( E ) . Определим на борелевских множествах

Е с Mq следующие функции множеств цх (E )= lim (Ym )+(E),  М2(E )= lim (Ym )-(E).

m ^rc

Эти функции положительны.

Пусть E – дизъюнктная последовательность борелевских множеств rc rc

E = U Ei . Имеем М1 (E) = lim (Ym )+ (E) = lim Z(Ym )+ (E ). m ^rc i=1

Так как (Y_m )₊ ( E .) <  м ( E ) , то справедливо неравенство м ( E ) <  ^ м ( E ) .

г = 1

kk

С другой стороны  м(E)> limy(Y,) (E)=Ум(E). Теперь легко вывести, m ^rc “   +     "

г = 1                            г = 1

что М ( E ) = ^ М ( E ) . Таким образом м — положительная борелевская мера.

i = 1

Если Е с #('J является компактом , то последовательность (y )+(Е) является стабилизирующейся. Поэтому мера ц локально конечная. Аналогично доказывается, что ц - положительная локально конечная борелевская мера.

Если борелевское множество Е такое, что Е с R Q - компакт, то для достаточно больших n имеем ц ⁽ E ) -ц ⁽ Е ) = ^ )₊ ⁽ E ) - ^ т ) —⁽ E ) =у _т ⁽ E ) = ц⁽ E ) .

Тем самым элемент ц эквивалентен ц - ц . Обозначим через

А (2)= A <²) n [ в ( 0,2 ) \ C ( 0,1 I         I 2

Л

А ( ^т ) = A m П

)

в ( 0, т ) \ C f 0,— )

V т ))

\ в ( 0, т - 1 ) \ C ( 0,1 ))

V            V ^{т - 1} )))

да

, т > 2, А1 = U А(n), т=2

А 22 ) = A 2² ) П

B ( 0,2 ) \ C ( 0,^- )

I         V 2 ))

А 2 ^т )

= a т n

/ X /   1 ^

в ( 0, т ) \ C | 0,— I

V ^т ))

\ в ( 0, т V

- 1 ) \ с I 0,

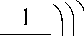
т - 1 )

, т >  2 , A ₂ = Q. Aⁿ ) . Выполняются соотношения А 1 U Л ₂ = R Q , АПА₂ = 0 .

т = 2

1 ))

Пусть E - борелевское множество, E с А₂П в ( 0, k ) \ C | 0,- I . V             V к ))

Имеем

(

k

ц ( E ) = l™ < Y - ) + ( E ) = Y k ( e n A ,“¹ ) = Y k E П U- A 1 ' '

V

V i = 1

= :t Y k ( e n - A f ' ’ ) = ]t y , ( e n . А () ) . i = 2                          i =

Из соотношений ED^Afт) с Ax,ЕП^АП с А следует, что ЕП^Аfт) =0,ц (E) = 0. Из сказанного следует, что ограничение меры ц на множество А, есть ненулевая мера и, значит, мера ц сосредоточена на множестве А,. Аналогично доказывается, что мера ц сосредоточена на А2. Поэтому меры ц и ц взаимно сингулярны. Теорема доказана.