Теорема о сходимости генетического алгоритма с двухуровневым кодированием к точному решению задачи реконфигурации плис
Автор: Городилов А.Ю., Данилова Е.Ю.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Информатика. Информационные системы
Статья в выпуске: 4 (31), 2015 года.
Бесплатный доступ
Приведена краткая постановка задачи реконфигурации ПЛИС, описаны базовый и генетический алгоритмы реконфигурации. Генетический алгоритм использует двухуровневое кодирование решений с промежуточным представлением в виде матрицы смежности полного двудольного графа. Сформулирована и доказана теорема о сходимости разработанного генетического алгоритма к точному решению задачи реконфигурации ПЛИС.
Генетический алгоритм, плис, реконфигурация, сходимость, оптимизация
Короткий адрес: https://sciup.org/14730015
IDR: 14730015 | УДК: 004.312+004.023
Текст научной статьи Теорема о сходимости генетического алгоритма с двухуровневым кодированием к точному решению задачи реконфигурации плис
Для решения задачи реконфигурации ПЛИС необходимо совершить несколько шагов. Первый из них – проведение диагностики, по результатам которой становится известно состояние каждого логического элемента (ЛЭ). Таких состояний может быть два: 0 – неработоспособный и 1 – работоспособный.
Эти данные можно представить в виде таблицы, называемой матрицей состояний и обозначаемой A . Для реконфигурации выбирается наиболее предпочтительный набор работоспособных элементов, расположенных максимально компактно. Множество используемых ЛЭ в системах конфигурации ПЛИС описывается набором прямоугольников (координатами их левого верхнего угла и размерами). Прямоугольники не должны пересекаться и не должны содержать неработоспособных ЛЭ. Чем меньше количество прямо-
угольников в описании, тем быстрее будет выполнена реконфигурация.
Пусть P x,y ( h , l ) – матрица размерности h х l , полученная из матрицы A удалением строк с номерами 1, 2, …, x -1, x + h , …, n и столбцов с номерами 1, 2, …, y -1, y + l , …, m . То есть
P x , y ( h , l ) =
x , y
a x , y + 1 - 1
^ a x + h - 1, y
a x + h - 1, y + 1 - 1 J
Элемент a x , y будем называть якорем матрицы P x , y . Если все элементы матрицы P x , y ( h , l ) равны 1, то это покрывающий прямоугольник . Количество элементов в нем назовем площадью покрывающего прямоугольника и обозначим S ( P ). Множество R покрывающих прямоугольников P 1 , P 2 ,…, P k назовем покрытием , если никакая пара покрывающих прямоугольников из этого множества не пересекается. Сумму площадей покрывающих прямоугольников, входящих в покрытие, назовем площадью покрытия и обозначим S ( R ).
Пусть t – количество ЛЭ, необходимых для реализации схемы устройства. Тогда задачу можно сформулировать так: дана матрица состояний A и число t . Найти покрытие площади ≥ t минимальной мощности. Данная задача является NP-трудной [1], поэтому на больших логических схемах точные алгоритмы будут работать неприемлемо долго. Следовательно, необходима разработка приближенных, эвристических алгоритмов.
Базовый приближенный алгоритм
Покрывающий прямоугольник P x,y ( h 0 , l 0 ) назовем локально-максимальным , если не существует покрывающего прямоугольника большей площади с тем же якорем.
На основе этого определения можно предложить следующий алгоритм решения задачи:
-
1. R ← ∅ .
-
2. Установить порядок просмотра элементов матрицы A .
-
3. Выбрать очередной элемент a x , y из матрицы A в соответствии с установленным порядком.
-
4. Найти локально-максимальный покрывающий прямоугольник P x , y ( h 0 , l 0 ) с якорем a x , y .
-
5. R ← R ∪ P x , y ( h 0 , l 0 ).
-
6. Обнулить все элементы матрицы A , входящие в P x , y ( h 0 , l 0 ): a ij ← 0, i = x .. x + h 0 -1, j = y .. y + l 0 -1.
-
7. Вычислить, сколько «единиц» еще нужно покрыть: t ← t - h 0 ⋅ l 0 .
-
8. Если t >0, перейти к шагу 3.
-
9. Покрытие R является решением задачи.
Данный алгоритм работает быстро, но не всегда находит точное решение, то есть не всегда найденное количество покрывающих прямоугольников оказывается минимальным. Очевидно, что результат работы алгоритма может зависеть от установленного в шаге 2 порядка просмотра элементов.
Генетический алгоритм
Для разработки генетического алгоритма (ГА) необходимо в первую очередь определить структуру хромосом и функцию приспособленности. Принимая во внимание алгоритм α, решение может быть найдено в виде последовательности, задающей порядок просмотра элементов матрицы состояний. Неработоспособные элементы можно сразу ис- ключить из рассмотрения. Таким образом, длина каждой хромосомы L будет фиксирована и равна количеству "1" в таблице состояний. Но сама такая последовательность s (перестановка на множестве работоспособных ЛЭ) является только особью, но не может кодироваться в виде хромосомы, поскольку гены (элементы перестановки) зависят друг от друга. Чтобы обеспечить независимость генов, закодируем перестановку с помощью промежуточного объекта. В качестве такого объекта предлагается совершенное паросоче-тание в полном двудольном графе. Хромосомой при этом будет сам граф, заданный в виде матрицы смежности. Такое представление обладает двумя основными свойствами: независимость генов (элементов матрицы) и существование эффективной процедуры преобразования в перестановку, для этого достаточно упорядочить все ребра паросочетания по вершинам первой доли (перестановку образуют вершины второй доли). Процедуру преобразования будем обозначать Present. Для поиска самого паросочетания в графе используется эффективный "венгерский алгоритм", который находит правильный ответ за полиномиальное время [2].
Подробное описание операторов двухуровневого ГА и промежуточного представления можно найти в [3, 4, 5].
Приспособленность особи определяется после запуска алгоритма α как величина, обратная к мощности множества R.
Обоснование сходимости генетического алгоритма к точному решению
ГА относятся к числу эвристических методов, поэтому строгое доказательство сходимости получить невозможно. Но использование стандартных классических операторов в предложенном ГА позволяет принять во внимание все существующие теоретические обоснования и экспериментальные подтверждения эффективности генетических алгоритмов.
Единственное, что отличает предложенный алгоритм от классических – это оригинальный способ кодирования и, соответственно, вычисления приспособленности особей. Следовательно, необходимо проверить три условия, которым должна удовлетворять фитнесс-функция в классических ГА.
-
1. Потомки, получающиеся в результате скрещивания, должны быть «похожими» на своих родителей.
Это означает, что в результате скрещивания двух перестановок должны получаться перестановки, «похожие» на родительские особи. Термин «похожими» в данном случае формализовать невозможно. Будем исходить из такой трактовки этого термина: перестановки должны совпадать значениями отдельных элементов в некоторых позициях. Пусть особи µ3 и µ4 являются потомками особей µ1 и µ2, s 1=Present (^1) = (i[ i 2 ... i 'L), s2=Present(^2)=(i1'' i" iL), s 3=Present (^з )=(j' j 2 ... j'L), s4=Present(^4 )=(j‘' j22 jL).
Нас интересуют позиции k , в которых значение элемента потомка j'k совпадает со значением соответствующего элемента в одном из родителей, то есть с i k или i k . Обозначим через Sum 1 количество таких номеров k для первого потомка, а через Sum 2 – для второго. То есть,
L
Sumi = £ I((jk = ik) v (j k = ik)), k=1
L
Sum 2 = £ I (( J k = i‘ k ) v ( j k = i k ) .
k = 1
Общее количество позиций, в которых может быть совпадение элементов перестановок, очевидно, равно 2 L . Таким образом, нас
Sum, + Sum7 интересует отношение Q = -----------, ко-
2L торое имеет смысл доли генов в потомстве, унаследованных от родителей, и выражает степень «похожести» потомков на предков.
К сожалению, теоретически нельзя гарантировать, что параметр Q будет достаточно большим, поэтому значение Q проверялось эмпирически. Для проведения эксперимента было сгенерировано 35 матриц размерности 11, заполненных случайными числами. Далее 80 раз был запущен оператор скрещивания, и для каждого запуска определялось значение параметра Q . По полученным данным можно сделать следующие выводы:
-
• во всех случаях параметр Q превысил значение 0,4;
-
• более чем в 90 % случаев параметр Q превысил значение 0,5;
-
• среднее значение параметра Q составило 0,732.
-
2. Чем больше значение приспособленности особи, тем лучше должно быть решение, кодируемое данной особью.
-
3. Существует особь с максимальной приспособленностью, кодирующая точное решение задачи.
То есть в абсолютном большинстве случаев потомками от родителей наследуется по меньшей мере половина значений, что можно признать вполне приемлемым результатом.
Выполнение данного условия гарантируется непосредственно правилом вычисления приспособленности: чем больше величина 1/|R|, тем меньше |R|, т. е. меньше количество задействованных прямоугольников и, следовательно, элементы располагаются более компактно.
Для проверки данного условия докажем следующую теорему.
Теорема. Существует последовательность просмотра элементов ar „ ,a. „ ,.,a, „ такая, что выполнение x1 ,y1 x2 ,y2 xk ,yk алгоритма α дает точное решение задачи.
Доказательство. Обозначим точное решение задачи R *, а решение, полученное алгоритмом α, обозначим R . Докажем, что для любых матрицы A и числа t существует такая последовательность просмотра элементов, что | R |=| R *|. Доказательство выполним по индукции по мощности покрытия R * для пары ( A , t ).
База индукции | R *|=1. То есть R * = { P * x , y ( h 1 , l 1 )}. Тогда очевидно, что последовательность, состоящая из одного элемента ( a x,y ), является искомой. Действительно, в локально-максимальном покрывающем прямоугольнике P x,y ( h 0 , 1 0 ): h 0 • 1 0 > h 1 • 1 1 > t , т. е. R = { P x,y ( h 0 , l 0 )} и | R |=| R *|=1.
Индукционный переход . Пусть утверждение справедливо для всех пар ( A , t ), для которых | R *|= k -1. Докажем, что оно будет справедливо и для пар, в которых | R *|= k .
Лемма 1 . В оптимальном покрытии R * найдется покрывающий прямоугольник P * u,v ( h 1 , l 1 ) такой, что локально-максимальный покрывающий прямоугольник с тем же якорем P u,v ( h 0 , l 0 ) попарно не пересекается ни с одним из остальных покрывающих прямоугольников из R *, то есть
3 P v ( h i , l i ): V P * e R *, P * * P^ ( h i , l i ):
, , (2)
P Лh 0, l 0) n P =0 .
Доказательство
Предположим противное:
-
V P v ( h 1 , 1 1 ): 3 P * e R *, P * * C ( h 1 , 1 1 ): (3) P u , v ( h 0 , 1 0 ) n P * *0 .
Пусть R* = {px* y ,Px* y ,_,Px* y }. По-x1 ,y1 x2 ,y2 xk ,yk строим ориентированный граф G=(V,E). Отметим, что множество вершин соответствует множеству якорей покрывающих прямоугольников из R*:
V = { v 1 , V 2 , - , v k }, v , = ax , yi, i = 1, k .
Ребро
*
( V i , V j ) e E ° P x, , y i ( h 0 , 1 0 ) n P xj , y j ( h j , l j ) * 0 .
То есть ребро идет из вершины i в вершину j , если локально-максимальный покрывающий прямоугольник с якорем в i -той вершине пересекается с покрывающим прямоугольником с якорем в j -той вершине.
Лемма 1.1
-
P, v. ( h ', l ' ) n Px. v. ( h '' , l '' ) * 0 о x ' + h ' > x" л x , y x , y
x' < x” + h” л y ' +1 ' > y " л y' < y" + l''.
Доказательство
^ Пусть a x , y e P, , y ( h ', l ') n P^ , y . ( h' ", l ").
Тогда ax,y e Px',y•(h'l I') ^ x > x'
ax e P, „ ( h" , l" ) ^ x < x " + h" x , y x , y
____„ I II , 1 II
^^
x
Остальные неравенства доказываются аналогично.
^. Возьмем x = max(x', x"). Очевидно, x > x', x > x". Поскольку x'< x ' + h' и x" < x ' + h', то x < x ' + h'. Аналогично дока- зывается, что x < x " + h", y < y' + Г y < y " +1". Таким образом, ax,y e Px.,y (h', l ‘), ax,y e Px.,y (h", l"), что и требовалось доказать.
Следствие 1.1
( v i , v j ) e E ^ x i + h 0 > x j л xi < x j + h j л y i + 1 0 > y j л y , < y j + l j .
и
Лемма 1.2
( V , v j ) e E ^ y j > y , v x j > x i .
Доказательство
Предположим противное, и y j < y i л x j < x i . По следствию 1.1 x i < x j + h j и y i < y j + l j . Следовательно,
x, < x, < x, + hл v. < y < v. +l. ^
j i j j j i jj ax,, у, e Pj yj( hj, lj).
Кроме того, очевидно, ax,y e P* y (hi, li). Но два покрывающих прямоугольника из покрытия R* не могут иметь общих элементов. Возникает противоречие. Лемма 1.2 доказана.
В соответствии с ( 3 )
*
V i 3 j , j * i : P x,,y i ( h 0 , 1 0 ) n P xj,yj ( hj , l j ) * 0 .
То есть, из любой вершины графа G есть хотя бы одно исходящее ребро. Следовательно, в графе G есть ориентированный цикл. Пусть его образуют вершины v 1 , v 2 ,…, v w . Далее будем рассматривать только вершины и ребра, составляющие этот цикл.
На основе графа G =( V , E ) (точнее, вершин и ребер, образующих ориентированный цикл) построим ориентированный ортогональный граф H =( U , E H ) на плоскости по следующим правилам. Вершины:
vt = ax y e V ^ ut = ( xt , y z-) e U .
xi , yi
Ребра. В соответствии с леммой 1.2 возможны три типа ребер в графе G (рис. 1 ).
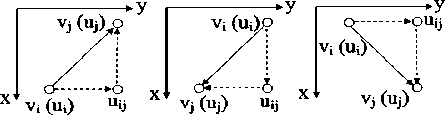
Рис. 1. Возможные ребра в графе G
Тип 1. y j > y i , x j < x i . Добавим в граф H вершину u ij = ( x i , y j ) и пару ребер: горизонтальное ( u i , u ij ) и вертикальное ( u ij , u j ) (в случае x j = x i вершина u ij совпадает с вершиной u j и вертикальное ребро отсутствует). Заметим, что если точка ( x , y ) лежит на ребре ( u ij , u j ), то y = y j , x j < x < x i .
По следствию 1.1, x i < x j + h j .
Из указанных соотношений получаем, что y=yj, xj Тип 2. yj < yi, xj > xi. Действуем аналогично, добавляя вершину uij = (xj, yi) и пару ребер: (ui,uij) и (uij ,uj) . Если точка (x, y) лежит на ребре (uij, uj), то x=xj, yj Тип 3. yj > yi, Xj > xi. Добавим в граф H вершину uij = (xi,yj) и пару ребер: горизонтальное (ui, uij) и вертикальное (uij , uj) . По построению граф H представляет собой граф-цикл. Пусть yr = max(у 1,у2,...,yw). Рассмотрим соответствующую вершину vr (если для нескольких вершин y=yr, возьмем вершину с минимальным значением x). Пусть вершине vr инцидентны ребра (vi,vr),(vr,vj). Поскольку у>yj-, ребро (vr, Vj) относится к типу 2. В случае yr=yi, согласно лемме 1.2, xr>xi, но в случае равенства мы выбирали в качестве vr вершину с минимальным значением x. Значит, yr>yi и ребро (vi,vr) относится к типу 1 или к типу 3. Разберем эти случаи. Случай 1. Ребро (vi,vr) относится к типу 1 (рис. 2). Рис. 2. Варианты расположения ребер, инцидентных вершине vr. В графе H получим последовательность ребер (ui,uir),(uir,ur),(ur,urj),(urj,uj), где ur=(Xi,yr),Urj=(Xj,yr),yr>yi,Xr Последовательность двух вертикальных ребер (uir,ur),(ur,urj) заменим одним ребром (uir,urj). Определим его направление. P*,yr (hr , lr ) ^ Pj,yj (hj , lj ) = 0 , поэтому по лемме 1.1: Xr + hr < Xj v Xr > Xj + hj v Уг+lr< yj vУг > yj+lj. Из (7) получаем Xr<Xj<Xj+hj, yj<yr<yr+lr, следовательно, в выражении (8) второе и третье неравенства не выполняются. (vr, Vj) e E, поэтому по следствию 1.1: yr < yj + lj, то есть в выражении (8) четвертое неравенство тоже не выполняется. Значит, должно выполняться первое неравенство: Xr + hr < Xj. (vi, vr) e E, поэтому по следст вию 1.1: Xi < Xr + hr. Получаем Xi< Xr + hr< Xj. Таким образом, ребро (uir,urj) будет направлено вниз. Вся фигура, ограниченная графом-циклом H, располагается в правой полуплоскости относительно ребра (uir,urj), т. е. цикл H имеет ориентацию по часовой стрелке. Случай 2. Ребро (vi,vr) относится к типу 3 (рис. 2). В графе H получим последовательность ребер (ui,uir),(uir,ur),(ur,urj),(urj,uj), где Uir=(Xi,Уг), Urj=(Xj,Уг),Уг>У., Xr>Xi,yj<Уг , Xj>Xr. (9) Последовательность двух вертикальных ребер (uir,ur),(ur,urj) заменим одним ребром (uir,urj). В соответствии с (9): xj>xr>xi. Таким образом, ребро (uir,urj) будет направлено вниз. Вся фигура, ограниченная графом-циклом H, располагается в правой полуплоскости относительно ребра (uir,urj), то есть цикл H имеет ориентацию по часовой стрелке. В обоих случаях мы получили, что цикл H имеет ориентацию по часовой стрелке. Точки самопересечения (если они есть) разбивают цикл H на несколько отдельных замкнутых частей без самопересечений. Рассмотрим ту часть, которая включает в себя ребро (uir, urj). По доказанному выше, этот цикл имеет ориентацию по часовой стрелке. Рассмотрим самые левые точки этого цикла и выберем из них самую нижнюю. Пусть это будет точка (x,y). Учитывая выбор точки (x, y) и тот факт, что все ребра цикла строго вертикальны либо горизонтальны, точка (x, y) находится на пересечении горизонтального ребра (u',u'') и вертикального ребра (u''',u'''') (возможно, в вершинах этих ребер). Учитывая ориентацию цикла (части цикла), ребро (u',u'') ориентировано справа налево (цикл расположен выше), а ребро (u''',u'''') – снизу вверх (цикл расположен справа). Анализируя все возможные типы ребер, перечисленные выше, получаем, что ребро (u',u'') получается только из ребра типа 2 и является ребром вида (uij ,uj) , а ребро (u''',u'''') – из ребра типа 1 и является ребром типа (urt,ut) . При рассмотрении ребер типа 2 было установлено, что, согласно (6), если точка (x,y) лежит на ребре (uij ,uj) , то aX,ye P* y^ . При рассмотрении ребер типа 1 было установлено, что, согласно (5), если точка (х,у) лежит на ребре (urt, ut), то aX,уePX*,yt . Но тогда получается, что Px* „ (h,, l,) n Px*„ (ht, L) ^0, что возможно xj ,yj j j xt ,yt t t только при j=t, i=r. Но тогда ребро (vi,vj)=(vr,vt) относится одновременно и к типу 1, и к типу 2, что невозможно. Получили противоречие. Доказательство леммы 1 завершено. Вернемся к доказательству теоремы. Рассмотрим оптимальное покрытие R*. Согласно доказанной лемме 1, в нем найдется покрывающий прямоугольник P*u,v(h1,l1) такой, что локально-максимальный покрывающий прямоугольник с тем же якорем Pu,v(h0,l0) попарно не пересекается ни с одним из остальных покрывающих прямоугольников из R*. Обнулим элементы матрицы A, входящие в Pu,v(h0,10). Получим матрицу A’ = (ai j): a,j,i e [1;u -1] u[u + ho;n] v , _ je[1;v-1] u[v +10;m] ail'.. 0, i e [u; u + h0-1] л , j e [v;v +1о -1]. Обозначим t ' = t - ho • lo, R '* = R *\ P v (h1,11). | R '*| = R *\P, v (h1,11)| = R *| -1 = k -1. Лемма 2. Покрытие R'* является точным оптимальным решением рассматриваемой задачи для пары (A', t'). Доказательство. Во-первых, докажем, что R ‘* действительно является покрытием в матрице A'. Рассмотрим произвольный покрывающий прямоугольник P' e R'* и произвольный элемент aP e P'. Поскольку P‘ e R‘* c R* являлся покрывающим прямоугольником в матрице A, a„= 1. (11) С другой стороны, P 'e R *, P'* P:, v (^,11). Следовательно, по лемме 1, согласно (2): Pu,v(h0,10) nP' = 0 . То есть, поскольку a e P', a\, j £ Pu,v (ho, lo) ^ i e [1; u -1] и [u + ho; n] v j e[1; v -1] и [ v +1 o; m ] и, в соответствии с (10) и (11): ai j = ai j = 1. Таким образом, все элементы прямоугольника P' в матрице A' равны 1, то есть он является покрывающим, а R '* является покрытием. Во-вторых, S (R ‘*) = S (R *) - S (Pv (h1,11)) = . S(R*) -h1 • 11 > t-h0• 10= t'. То, что мощность R '* минимальна, легко доказать от противного. Доказательство леммы 2 завершено. Возвращаемся к доказательству теоремы. Итак, покрытие R '* является точным оптимальным решением рассматриваемой задачи для пары (A', t ')и R '*| = к -1. Значит, по предположению индукции, существует последовательность просмотра элементов ar „ ,ar „ ,...,ar „ такая, что выполнение x1, y1 ’ x 2, y 2’ ’ xk-1, yk-1 ’ алгоритма α дает точное решение задачи для пары (A', t'). Обозначим это решение R'. IR'| = R'*| = k -1. Тогда при выполнении алгоритма α для пары (A, t) с последовательностью a ,a ,a , . ,a при первой u,v’ x 1, y 1’ x 2, y 2’ ’ xk-1, yk-1 r r итерации на шаге 4 будет выбран прямоугольник Pu,v(h0, l0) , на шаге 6 будет построена матрица A', а на шаге 7 вычислено t' = t - h0 • 10. После первой итерации мы получаем задачу для пары (A', t') и последовательность ar „ ,ar „ ,....ar „ . Дальнейшее x1, y1 ’ x 2, y 2’ ’ xk-1, yk-1 выполнение алгоритма даст покрытие R'. Результатом алгоритма α для пары (A, t) будет покрытие R = Puv (h0,10) u R', которое является точным решением задачи. Действительно, R по построению является покрытием с площадью > t и I R| = Pu, v (h 0,10) u R '| = 1 + k -1 = k = |R*|. Теорема доказана. Таким образом, действительно существует особь генетического алгоритма, кодирующая точное решение задачи. В силу справедливости условия 2, приспособленность такой особи, очевидно, максимальна. Заключение Одним из спорных моментов любого эвристического алгоритма, к которым относятся и генетические алгоритмы, является сходимость. В данной статье приведена и доказана теорема о сходимости генетического алгоритма с двухуровневым кодированием для задачи реконфигурации ПЛИС. Были проверены условия сходимости для фитнесс-функции ГА, подробно доказано наиболее интересное условие – существование особи с максимальной приспособленностью, кодирующей точное решение задачи реконфигурации. Кроме того, был подробно описан базовый приближенный алгоритм поиска покрытия, который используется для вычисления фитнесс-функции.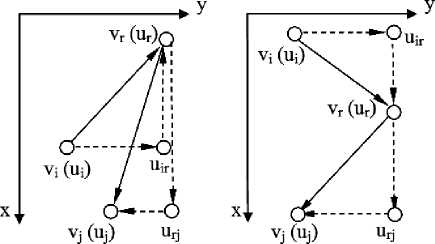
Список литературы Теорема о сходимости генетического алгоритма с двухуровневым кодированием к точному решению задачи реконфигурации плис
- Еремеев А.В., Заозерская Л.А., Колоколов А.А. Задача о покрытии множества: сложность, алгоритмы, экспериментальные исследования. Дискретный анализ и исследование операций. Сер. 2. 2000. Т. 7, № 2. С.22-46.
- Асанов М. О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы. НИЦ "Регулярная и хаотическая динамика": Ижевск, 2001.
- Данилова Е. Ю., Городилов А. Ю. Сравнение генетических алгоритмов на примере задачи коммивояжера//Вестник Пермского университета. Математика. Механика. Информатика. Пермь: ПГУ, 2009. Вып. 3 (29). С. 49-53.
- Городилов А. Ю. Двухуровневый генетический алгоритм для решения задач выделения компактных групп объектов//Междисциплинарные исследования: сб. матер. науч.-практ. конф. Перм. гос. нац. исслед. ун-т. Пермь, 2013. Т. 1. С. 190-193.
- Городилов А.Ю. Двухуровневый генетический алгоритм реконфигурации программируемых логических интегральных схем//Information Technologies and Knowledge. 2014. Vol. 8, № 2. P. 131-140.


