Теорема об общем виде линейного непрерывного функционала в пространстве непрерывных финитных функций
Автор: Нгуен Ван Куинь
Журнал: Мировая наука @science-j
Рубрика: Естественные и технические науки
Статья в выпуске: 6 (51), 2021 года.
Бесплатный доступ
Теория меры играет важную роль в теории субгармонических и -субгармонических функций. Классические свойства меры были представлены во многих монографиях, например в [1]. В статье представляется усиление варианта Азарина теоремы об общем виде линейного непрерывного функционала в комплексном пространстве непрерывных финитных функций. Результаты нашей статьи позволяют несколько упростить конструкции из этих работ.
Мера хана, мера жордана, сингулярная положительная мера, линейный непрерывный функционал
Короткий адрес: https://sciup.org/140266165
IDR: 140266165
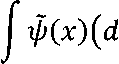
Список литературы Теорема об общем виде линейного непрерывного функционала в пространстве непрерывных финитных функций
- Kadets, V.M. (2006), A course of Functional Analysis, Kharkov National University.
- Van Quynh Nguyen (2015), Various Types of Convergence of Sequences of Subharmonic Functions, Zh. Mat. Fiz. Anal. Geom,Volume 11, Number 1, 63-74.
- Nguyen Van Quynh, Theorem on uniform continuity of Logarithmic potential, Visnyk of science and education, Issue 5 (59), 6-10p.
- Nguyen Van Quynh, Le Anh Thang (2021)
Статья научная
