Теоремы о неявном операторе в секториальных квазиокрестностях и минимальные ветви решений нелинейных уравнений

Пусть X , У - банаховы пространства, Л - линейное нормированное пространство. Рассматривается нелинейное операторное уравнение

F(ж, А) = 0,                                       (1)

где F : X ф Л — У У, F(0,0) = 0, оператор F_c(0,0) не является непрерывно обратимым. В работе, продолжающей исследования [1], [2], доказано существование непрерывных решений уравнения ж (А) -» 0 при А —> 0 в секториальной квазиокрестности нуля и дан способ их построения. Результатом работы являются теоремы существования минимальных ветвей максимального порядка малости решений нелинейных уравнений и дополняют результаты [1].

Определение 1. Секториальной квазиокрестностью точки 0 € Л будем называть открытое множество S С Л, такое что 0 € 8S.

Далее пусть а(А) некоторая функция а(А) : S —> R^, а(А) —> 0 при S Э А —> 0. Вводится множество П = {(ж, А) € X ф Л, ||ж|| < a(A)r, А € S}, где г > 0. Доказаны следующие теоремы.

Теорема 1. Пусть в Q выполнены условия: 1) оператор F(x, А) непрерывен по х и А и имеет частную производную Фреше ^(ж, А), непрерывную по х и X; 2) F(0,0) = 0, оператор F^O, А) непрерывно обратим при А € S, причем HF^¹^, А)|| = О(^щ);

• 3)    ||^ж,А)-^0,А)||<£||ж||;4) ||F(0,А)|| = о(а²(А)).

Тогда найдется число го € (0, г) и секториальная квазиокрестность нуля So С S такие, что для каждого А € So уравнение (1) имеет в шаре ||ж|| < а(А)го непрерывное решение ж(А) —> 0 при So Э X 0.

Доказательство. Уравнение (1) с помощью замены ж = a(X)V приводится к эквивалентному уравнению

У = Ф(У,А),                                 (2)

где оператор Ф(У, А) имеет вид

ф(_У, д) = у - -^Е'До, Х)Е(а(Ж А).

Нетрудно видеть, что оператор Ф(У,А) при X 6 S, ЦУЦ < го < г является сжатием. Действительно, применяя формулу конечных приращений Лагранжа и условие 3) теоремы, получим цепочку неравенств

||Ф(У₁,А)-Ф(У₂,А)|| < ||F-¹(0,A)|| j ||Е_х(0, А)-Е_$(а(А)(У₂+6(У₁-У₂)), А)М0 ||(Vi-V₂)|| < о

• < clJ {11^11 + 6(11^11 + ||V₂||)} de цу. - V2II <  гсш - уц, о

здесь С, L - const. Выберем tq <  2UL1 тогда оператор Ф(У, А) при А Е S и ||У || < го будет сжатием.

Более того, при достаточно малых А в силу оценки 4) оператор Ф(У, А) переводит шар ||У || < го в себя. Действительно,

||Ф(У,А)|| < ||Ф(уА)-Ф(0,А)||+||Ф(0,А)|| <щ-0+-^|^^^

Далее, в силу условия 4), можно выбрать множество So С S так, что при VA Е So будет выполнено ^у||Е(О, А)|| < (1 -д)г0.

Поэтому на основании принципа сжимающих отображений операторное уравнение (2) имеет единственное решение V (А) —> 0 при А -» 0. Возвращаясь к переменной ж получаем, что уравнение (1) имеет малое непрерывное решение, вообще говоря, не единственное. □

Если Ед, (0,0) ^ 0, то следующий результат позволяет в приложениях ослаблять условие 4) теоремы 1.

Теорема 2. Пусть выполнены условия 1) — 3) теоремы 1 и пусть выполнено условие:

• 5)    линейное уравнение ЕДО, 0)ж = Е(0, А), где А Е S, имеет решение ж*(А), причем выполнены оценки ||ж*(А)|| = о(а(А)) и ||ЕД0,0) — ЕДО, А)|| = О(а(А)) при А € S.

Тогда найдется число го € (0, г) и секториальная квазиокрестность нуля So С S такие, что для каждого А Е So уравнение (1) имеет в шаре ||ж|| < а(А)го непрерывное решение ж(А) -> 0 при So Э А —> 0.

Доказательство. Уравнение (1) с помощью замены ж = a^V приводится к эквивалентному уравнению (2).

Сжимаемость оператора Ф(У,А) вытекает из условий 1)-3). (см. док-во теоремы 1). Покажем, что при достаточно малых А Е So С S, оператор Ф(У, А) переводил шар ||У|| < го в себя. Действительно, в силу условия 5) имеем цепочку неравенств

||Ф(И,А)|| <^о + -^-||Е-1(О,А)Е(О,А)|| =

= 9го + ^^^^^{ЕДО^) -ЕДО, А) + ЕДО, А)}ж*(А)||< 9г0 + ^у||ж*(А)||.

В силу оценки из условия 5) при достаточно малых А Е So С S выполнится неравенство ^щ||ж*(А)|| < (1 — у)го, где С - const. Следовательно, ||Ф(У, А)|| < го при ЦУЦ < го и А Е Sq.

□

Р.Ю. Леонтьев

Пример 1. Покажем, что уравнение

F(x, А) = J tsx(s) ds + Xx(t) — J ж3(а) ds — f(t,X) = 0,(6)

оо где x(t) E Цод]) /(Л A) — ш(^)Ап, m^t) E Срд], n > 2, S - суть проколотая окрестность нуля, имеет малое непрерывное решение хх^ —» 0 при S Э А —> 0. Здесь дифференциал Фреше имеет вид

ЕДж, А)/г = J tsh(s) ds + Xh(t) — 3 j" x2(s)Ms)ds, оо при этом

^(0, x)h =             /sh^ds.

Л ^иА A J О

Далее, ЕДО, 0) = 0 и выполнена оценка

||Г1-1(0,А)||=оШ.

Условия 1), 2) очевидно выполнены. В силу неравенств

WF^xA^h-F^X^hW = ||з jx4sMsW\\< Зг||ж|| Ц/гЦ о условие 3) тоже выполнено. Если п > 2, то выполнено условие 4), и по теореме 1, уравнение имеет малое непрерывное решение жд(£) —»■ 0 при А —> 0. Если п = 2, то условие 4) не выполняется, но будет выполнено условие 5), если т^ = const-t. Таким образом, для того, чтобы данное уравнение при п = 2 имело решение жД<) —> 0 при А —> 0, достаточно, чтобы m(<) = const • t.

Пример 2. Покажем, что двухточечная краевая задача для интегро-дифференциальной системы

' ~у"(*) = ®(<), у(0) = у(1) = 0, 0 <  t < 1

,                                     1

у^ + Аж(£) + tf x(s)y(s) ds + f(t, A) = 0, A > 0

.                               о где f(t,X) = m(t)Xn, m(t) E Т2[0д], n > 2, имеет малое непрерывное решение Vcx^yx^ -> (0,0) при А -> +0.

Из первого уравнения системы имеем y^t) = J G(t, s)x(s) ds, где

о

QU _s\ _ / ^C¹ ~ ^s)’ 0

’      [ (1 — t)s, s < 1.

Подставляя полученное выражение для y(t) во второе уравнение получим нелинейное интегральное уравнение:

Г(ж,А)

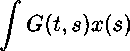
ds + Аж(<) + 1

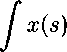
о

Проверим выполнение условий теорем. Очевидно, F(x, А) и F_x(x, Л) непрерывные операторы по ж и А. Далее, ЕДО, 0) = 0, а оператор Е_г(0, А) непрерывно обратим при А > 0, причем выполнена оценка ||F^"¹(0, А)|| = О (^). Таким образом, выполнены условия 1), 2). Условие 3) справедливо ввиду оценки:

||Е_х(ж, А)/г - F_x

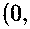
1 1

о о

1 1

G(s,z)(x(s)h(z) + h(s')x(z')') dzds <

< 11*11 • И • IMI • / l2\Ms,z^\dzdsо о

Условие 4), очевидно, выполнено при п > 2. Поэтому, по теореме 1, при п > 2 уравнение имеет малое непрерывное решение {жд (Z), т/д (t)} —> (0,0) при А —> +0. Если п = 2, то условие 4) не выполняется, но выполнится условие 5), если m(i) дважды дифференцируемая функция, причем т(0) = т(1) = 0. Таким образом, для того, чтобы данное уравнение при п = 2 имело решение ^xx^.yxU)^ -^ (0,0) при А —> +0 достаточно, чтобы m(i) была дважды дифференцируемой функцией, причем m(0) = т(1) = 0.

При проверке условий теорем 1, 2 в ряде приложений можно использовать следующий результат Н.А. Сидорова об обратимости оператор функций в окрестности фредгольмовых точек.

Рассматривается оператор-функция В — ХА, где В, А — замкнутые линейные операторы, действующие в банаховых пространствах, с плотными областями определения, Р(В) С Р(А). Фредгольмов оператор В имеет канонический полный А-жорданов набор (см. [3, гл. 9], [4]). Пусть l^}, {^1}}, г = 1, п — базисы в М(В) и М(В*) соответственно, проекторы п Pi                           П Pi г=1 7=1                       i=l 7=1

где В<р^ = Ар^-1\ В*1^ = A*^3-1\ 7р) = A(p^Pl+1"”3\ z^ = А*^1*1-3^ и ограниченный оператор гнв+П-лР’К’ г=1

соответствуют этому жорданову набору. Известно, что канонические полные наборы существуют и проекторы F и Q могут быть построены, если А = 0 — изолированная особая фредгольмова точка, т.е. оператор В — АА непрерывно обратим в окрестности 0 < |А| <  р (или, эквивалентно, рВ — А, в окрестности R < |д| < +оо).

Теорема 3. Оператор В—ХА непрерывно обратим в окрестности 0 < |А| < р тогда и только тогда, когда В имеет канонический полный А-жорданов набор. Причем при А < рр|| п Pi з

(В - АА)^-1 = Г (Z — ААГ)-¹ (Z - Q) -    52 52 ^Л"' \ ",                 ■   (И)

г=1 7=1 з=1

Теорема дополняет один известный результат о жордановых наборах (см. [3, гл. 9], [4]), так как здесь приводится компактное явное представление обратного операто-

Р.Ю. Леонтьев pa (В — А А) т. Доказательство тождества (11) использует {Р, 2}-сплетаемость операторов В, А, Г и представление единственного решения уравнения (В — АА) ж = / в виде ж = Гу + £"=1 ^^Сур^, где у = (I - ААР)-1 (I - Q) f. Вектор С из пространства ДР1+-+Р" определяется из системы линейных алгебраических уравнений с обратимой блочно-диагональной матрицей.

Следствие 1. Оценка ||(В — АА)"¹^ ~ -^ при А —> 0 (соответственно, оценка (цВ — А)^-1 ~ С|ц|^р-1 при у —> +ooj выполнена тогда и только тогда, когда р = max(pi,...,p_n).

Замечание 1. р = 1 тогда и только тогда, когда det l/Ay^, ^Л!    ^ 0.

L \             / J г,к=1

Автор благодарен профессору Н.А. Сидорову за постановку задачи и ценные замечания.