Теоремы типа Лиувилля для решений стационарного уравнения Шредингера с конечным интегралом Дирихле
Автор: Лосев Александр Георгиевич, Филатов Владимир Владимирович
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Математика труды III международной конференции "Геометрический анализ и его приложения"
Статья в выпуске: 5 (36), 2016 года.
Бесплатный доступ
В данной работе изучаются вопросы сохранения лиувиллева свойства для решений стационарного уравнения Шредингера с конечным интегралом Дирихле на произвольных некомпактных римановых многообразиях. Доказан аналог теоремы Альфорса о существовании нетривиальной ограниченной гармонической функции с конечным интегралом Дирихле.
Интеграл дирихле, стационарное уравнение шредингера, теоремы типа лиувилля, теорема альфорса, римановы многообразия
Короткий адрес: https://sciup.org/14969025
IDR: 14969025 | УДК: 517.956.224 | DOI: 10.15688/jvolsu1.2016.5.2
Текст научной статьи Теоремы типа Лиувилля для решений стационарного уравнения Шредингера с конечным интегралом Дирихле
DOI:
Данная работа посвящена изучению взаимосвязи между существованием нетривиальных ограниченных и неограниченных решений стационарного уравнения Шредингера
Lu = Au — c(x)u = 0 (1)
с конечным интегралом энергии (интегралом Дирихле)
D(M, и) = W ( |V u | 2 + c(x)u 2 ) dx (2)
м на произвольном некомпактном римановом многообразии М. Здесь с(ж) — гладкая неотрицательная на М функция.
Данная тематика имеет прямое отношение к теоремам типа Лиувилля. Считающаяся в настоящее время классической формулировка теоремы Лиувилля утверждает, что всякая ограниченная гармоническая функция в Rn есть тождественная постоянная. Нетрудно убедиться в справедливости следующих утверждений, называемых теоремами типа Лиувилля:
-
1) если и — неотрицательная гармоническая функция в Rn , то и является тождественной постоянной (иначе — выполнено HP(R n ) -лиувиллево свойство);
-
2) если гармоническая функция и в R n имеет конечный интеграл Дирихле J lV u l 2 dx,
R"
то и является тождественной постоянной (иначе — выполнено H.D(R n ) -лиувиллево свойство);
-
3) если и Е Lp(R n ) — гармоническая функция, где 1 < р < то , то и является тождественным нулем (иначе — выполнено HLp(R n ) -лиувиллево свойство).
В последние несколько десятилетий был опубликован ряд работ, посвященных получению аналогичных результатов на произвольных некомпактных римановых многообразиях. А именно, приводятся условия выполнения теорем типа Лиувилля на некомпактных римановых многообразиях в терминах роста объема, выполнения изопериметрических неравенств, условий на кривизну и так далее.
Одним из истоков указанной проблематики считается классификационная теория двумерных некомпактных римановых поверхностей. Отличительным свойством двумерных поверхностей параболического типа является выполнение для них теоремы Лиувилля, утверждающей, что всякая положительная супергармоническая функция на данной поверхности является тождественной постоянной. Данное свойство послужило основой для распространения понятий параболичности и гиперболичности на произвольные римановы многообразия.
А именно, многообразия, на которых всякая ограниченная снизу супергармоническая функция равна константе, называют многообразиями параболического типа (см. [10]).
К числу одного из первых результатов в определении типа риманова многообразия, использующих геометрические характеристики, относится теорема С.Я. Ченга и С.Т. Яу [8], утверждающая, что полное многообразие является параболическим, если объем геодезического шара радиуса R растет не быстрее, чем R 2 при R ^ то . Однако существуют многообразия параболического типа с произвольным ростом объема геодезического шара.
В работе [3] А.А. Григорьян доказал, что параболичность типа полного риманова многообразия М эквивалентна тому, что вариационная емкость любого компакта в М равна нулю.
Вообще, поиски признаков параболичности типа имеют большую историю. Общее представление о современных исследованиях в данном вопросе можно получить, например, из работы А.А. Григорьяна [10].
В ряде работ рассматривались аналогичные задачи для линейных эллиптических уравнений более общих, чем уравнение Лапласа — Бельтрами. В частности, достаточно серьезный интерес вызывает изучение асимптотического поведения решений стационарного уравнения Шредингера (1). Отметим, что в этом случае ненулевая постоянная не является решением, поэтому и лиувиллево свойство для него формулируется несколько иначе.
А именно, говорят, что на римановом многообразии M выполнено LB(M ) — ли-увиллево свойство, если любое ограниченное решение уравнения (1) есть тождественный нуль.
Приведем некоторые примеры. В работе А.А. Григорьяна [4] было показано, что выполнение LB(M ) — лиувиллева свойства для стационарного уравнения Шредингера с потенциалом с(ж), имеющим компактный носитель, эквивалентно параболичности типа риманова многообразия М .
Оценкам размерностей различных пространств решений стационарного уравнения Шредингера посвящены работы [5; 6].
Отдельный интерес вызывает вопрос о взаимосвязи выполнения теорем типа Лиувилля на некомпактных римановых многообразиях. Очевидно, что из выполнения HD(M ) -лиувиллева свойства следует выполнение HBD(M ) -лиувиллева свойства. Действительно, если любая гармоническая функция с конечным интегралом энергии есть тождественная постоянная, то любая ограниченная гармоническая функция с конечным интегралом энергии тоже будет являться константой. Вопрос: выполнено ли обратное включение, то есть следует ли из выполнения HBD(M ) -лиувиллева свойства выполнение HD(M ) -лиувиллева свойства?
Положительный ответ на данный вопрос дает известная теорема Л.В. Альфорса (см., например, [9]), которая утверждает, что если на многообразии M существует нетривиальная гармоническая функция с конечным интегралом Дирихле, то на M существует нетривиальная ограниченная гармоническая функция с конечным интегралом Дирихле. Целью данной работы было получить аналог теоремы Альфорса для решений уравнения (1), и, соответственно, показать эквивалентность LBD(M ) и LD(M ) -лиувиллева свойства.
1. Вспомогательные утверждения
Доказательство основных результатов опирается на классические утверждения теории уравнений с частными производными: принцип максимума, теоремы сравнения и другие аналогичные утверждения (см., например, [1, с. 39–41, 94–95]). Их справедливость на предкомпактных подмножествах некомпактных римановых многообразий доказывается также, как для ограниченных областей в евклидовом пространстве.
Напомним некоторые свойства решений уравнения
Lu = Au — с(ж)и = 0. (1)
Всюду далее будем считать, что M — произвольное некомпактное риманово многообразие. Лемма 1 (Принцип максимума). Пусть B — предкомпактное подмножество M с гладкой границей, тогда если
Lu = 0, то sup |u| = sup |u|.
В дВ
Лемма 2. Пусть B с M — произвольное предкомпактное открытое подмножество, {фг}^! — равномерно ограниченное на B семейство решений уравнения (1), ф, Е С2,а(В). Тогда семейство функций {ф«}°=1 компактно вместе с семейством их первых и вторых производных на любом компактном подмножестве В' с В.
Далее, пусть В — предкомпактное, открытое подмножество М с гладкой границей, и — дважды непрерывно дифференцируемая на В функция. Интеграл
D(B,u) = W (|Vu|2 + c(x)u2) dx в будем называть интегралом Дирихле функции и по множеству В.
Дальнейшие утверждения по своим формулировкам и методам доказательства близки к [7].
Лемма 3. Пусть В — предкомпактное подмножество М с гладкой границей. Семейство функций F = { y(x) Е С 2 (В) : D(B,y) < то} является линейным пространством со скалярноым произведением
( a, b ) = J ( (V a, V b ) + c(x)ab) dx, V a, b в
Е F.
Cоответствующая этому скалярному произведению норма
Ila|l = (a,a) 2 =
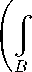
|Va | 2 + c(x)a2dx
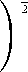
является интегралом Дирихле.
Лемма 4 (Принцип Дирихле). Пусть В с М — предкомпактное открытое подмножество М с гладкой границей. Для функций u,v Е С 2 (В) таких, что
( Аи — c(x)u = 0, x Е В, t и|дв = v|dB, выполнено
D(B,u) < D(B,v).
2. Взаимосвязь теорем типа Лиувилля
Теорема 1. Если на M существует нетривиальное решение уравнения
Lu = Аи — c(x)u = 0 (1)
с конечным интегралом Дирихле
J |V u | 2 + c(x)u 2 dx < то , (2)
м то на M существует нетривиальное ограниченное решение уравнения (1) с конечным интегралом Дирихле (2).
Доказательство. При доказательстве данного утверждения авторы воспользовались идеями, примененными в [2] при доказательстве теоремы, устанавливающей взаимосвязь между выполнением HD(M ) -лиувиллева свойства и существованием нетривиального решения некоторой внешней краевой задачи.
Предположим, что на M всякое ограниченное решение уравнения (1) с конечным интегралом Дирихле есть тождественный нуль, однако существует функция v, являющаяся нетривиальным неограниченным решением уравнения (1) с конечным интегралом Дирихле.
Пусть {В^}^1 — гладкое исчерпание, то есть последовательность предкомпактных ∞ открытых подмножеств M с гладкими границами, так, что В^ С Вk+1, IJ В^ = M. Так k=1
как v(x) = 0 , то обозначим
J |V v | 2 + c(x')v2dx = а > 0.
B i
Из сходимости интеграла J |V v | 2 + c(x)v 2 dx следует, что существует N такое, что м
J |V v | 2 + c(x)v 2 dx < а/4.
{ ж : |г; ( ж ) |> N }
Определим функцию-срезку vN функции v следующим образом vN (x) = <
v(x), x : | v(x) | < N N, x : v(x) > N
— N, x : v(x) < — N
Обозначим через u k решение следующей краевой задачи
Г Au k — c(x> k = 0, x G В к I u k W = v N ( x )l dB k
Пусть G С M — некоторое предкомпактное открытое подмножество M. Используя принцип максимума, получаем sup |uk| < sup |uk| = sup |uk| = sup |vN| < N G Bk dBk dBk при достаточно больших к. Следовательно, {uk}к=1 — равномерно ограниченное на G семейство решений уравнения (1). В силу леммы 2 оно компактно в классе С2(G). То есть на G существует подпоследовательность {ukt} такая, что lim uki = u. Покажем, kt^^
что на M существует сходящаяся подпоследовательность.
Далее будем в качестве множества G брать последовательно множества В k для к = 1, 2,.... Так как на В 1 { u k } k =1 компактно, то существует сходящаяся подпоследовательность { u k } такая, что lim u k = u 1 . В свою очередь, семейство { u k } компактно на k ^^
В 2 в классе С 2 (В 2 ) , и, следовательно, существует сходящаяся подпоследовательность
{и2 } последовательности { и к } такая, что lim и к = и 2 . Продолжая аналогичные рассуж- к ^^
дения, получаем последовательность функций {ик}, определенных на Вк. Определим функцию и следующим образом u1,x Е В1 и2, x Е В2\В1
и =
...
и к ,x Е В к \ В к - 1
...
Выберем подпоследовательность последовательности { и к } к =1 , сходящуюся к функции и . Пусть т 1 = и 1 ,т 2 = и 2 ,... ,т п = и ^ ,... , заметим, что т к сходится к функции и, по крайней мере поточечно. По лемме 2 из нее можно извлечь последовательность, сходящуюся по норме С 2 (G) . Применяя переобозначения, будем считать, что { и к } и есть эта подпоследовательность.
Для функции и выполнено Lu = 0 на произвольном предкомпактном подмножестве M, | и | < N . Покажем, что и имеет конечный интеграл Дирихле. Используя принцип Дирихле, получаем
J |V u 2 | 2 + c(x)u 2 dx < J |V v N | 2 + c(x^(u N ) 2 dx < J |V v | 2 + c(x)u 2 dx.
В к
В к
м
Переходя к пределу при к ^ то , получаем
J |V u |2 + c(x)u 2 dx < J |V v | 2 + c(x)v2dx.
м
м
Так как интеграл энергии от и сходится, то сходится и интеграл энергии от и.
Следовательно, и — ограниченное решение уравнения (1) с конечным интегралом энергии. В силу нашего предположения, и есть тождественный нуль. Следовательно, {ик} сходится к нулю в норме С2(G) (в частности, при G = В2). Из этого следует, что lim |Vu2 |2 + c(x)u2 dx = 0.
к ^^
В 2
Иначе говоря, существует к 1 такая, что при к > к 1 выполнено
J |V u k | 2 + c(x)^dx < а/6.
В 2
Рассмотрим последовательность z 2 = и — и к . Для z 2 выполнено
Г А^ к - c ( x)z 2 = 0, x Е В к 1 2 к 1 ЭВ к = u - B N 1 ЭВ к
.
Покажем, что
-
3 < J \^ Х к | 2 + c(x)z2 k dx. В 2
Из В1 С B2 получаем a = J |Vy|2 + c(x)y2dx < J |V((y — uk) + uk)|2 + c(x)((y — uk) + uk)2dx.
В 1
В 2
Используя неравенство треугольника | a + b | < | a | + | b | , получаем
W |V (( y - u k )+ u k ) | 2 + c ( x )((v - u k )+ u k ) 2 dx < W ( |Vz k | + |Vu k | ) 2 + c ( x )( z k + 2 z k u k + U k ) dx =
В 2 В 2
= J( |V z k | 2 + c(x)z k )dx + J( |V u k | 2 + c(x)u2 k )dx + 2 J( |V z k ||V u | + c(x)z k u k )dx.
В 2
В 2
В 2
Используя неравенство Коши 2ab < a 2 + b 2 , получаем
2 J |V z k ||V u k | + c(x^z k U k dx < J \V z k | 2 + c(x^z 2 dx + J \V u k | 2 + c(x)u2 k dx.
В 2
В 2
В 2
Таким образом, справедливо неравенство a = J |Vf|2 + c(x)y2dx < 2 I J |Vzk|2 + c(x)zkdx + J |Vuk|2 + c(x)ukdx I . В1 В2 В2
Следовательно, при к >к1 получаем а = J |Vy|2 + c(x)x2dx < 2 J |Vzk|2 + c(x)zkdx + 2a/6,
В 1
В 2
или,
3 < J |V z k | 2 + c(x)z k dx. В 2
Покажем, что
J |V z k | 2 + c(x)z k dx < 4
В 2
Используя принцип Дирихле, получаем
W |V z k | 2 + c(x)z k < W |V (y — y N ) | 2 + c(x)(x — x N ) 2 dx.
В к
Далее получаем
W |V (y — x N ) | 2 + c(x)(y — В к
= W |V (v — y N ) | 2 + c(x)(x
{ $ : | y(:r ) |> N }
В к
v N ) 2 dx < J |V (y — y N ) | 2 + c(x)(y — y N ) 2 dx = M
-
v N ) 2 dx + J |V (y — y N ) | 2 + c(x)(y — y N ) 2 dx.
{
ж
:
|г;
(
ж
)
|
Второй интеграл равен 0, так как на этом множестве v = v N . Для первого интеграла не сложно показать, что
W |V (v — v N ) | 2 + c(x)(v — v N ) 2 dx < W |V v | 2 + c(x)v2dx < ^.
{ ж : |г; ( ж ) |> N } { $ : | y (: r ) |> N }
В результате имеем
J \V z k | 2 + c(x)z 2 dx < J \V z k | 2 + c(x)z2dx < ^.
B 2 B k
Таким образом, получили противоречие a/3 < J \Vzk|2 + c(x)zkdx < a/4,
B 2
что и доказывает теорему.
Список литературы Теоремы типа Лиувилля для решений стационарного уравнения Шредингера с конечным интегралом Дирихле
- Гилбарг, Д. Эллиптические дифференциальные уравнения с частными производными второго порядка/Д. Гилбарг, M. Трудингер. -М.: Наука, 1989. -464 c.
- Григорьян, А.А. Лиувиллевы теоремы и внешние краевые задачи/А.А. Григорьян, Н.С. Надирашвили//Изв. вузов. Математика. -1987. -№ 5. -C. 25-33.
- Григорьян, А.А. О существовании положительных фундаментальных решений уравнения Лапласа на римановых многообразиях/А.А. Григорьян//Мат. сб. -1985. -Т. 128, № 3. -C. 354-363.
- Григорьян, А.А. Ограниченные решения уравнения Шредингера на некомпактных римановых многообразиях/А.А. Григорьян//Труды семинара И.Г. Петровского. -1989. -№ 14. -C. 66-77.
- Курмакаев, Р.Ф. Асимптотические свойства неограниченных решений эллиптических уравнений на модельных римановых многообразиях/Р.Ф. Курмакаев, А.Г. Лосев//Вестник Волгоградского государственного университета. Серия 1, Математика. Физика. -2012. -№ 2. -C. 30-40.
- Лосев, А.Г. Об асимптотическом поведении решений некоторых уравнений эллиптического типа на некомпактных римановых многообразиях/А.Г. Лосев, Е.А. Мазепа//Изв. вузов. Математика. -1999. -№ 6. -C. 41-49.
- Тиман, А.Ф. Введение в теорию гармонических функций/А.Ф. Тиман, В.Н. Трофимов. -М.: Наука, 1968. -207 c.
- Cheng, S.Y. Differential equations on Riemannian manifolds and their geometric applications/S.Y. Cheng, S.T. Yau//Comm. Pure and Appl. Math. -1975. -Vol. 28, № 3. -P. 333-354.
- Classification theory of Riemannian manifolds/S.R. Sario, M. Nakai, C. Wang, L.O. Chung. -Berlin; Heidelberg: Springer-Verlag, 1977. -498 p.
- Grigor’yan, A. Analytic and geometric background of recurrence and non-explosion of the Brownian motion on Riemannian manifolds/A. Grigor’yan//Bulletin of Amer. Math. Soc. -1999. -№ 36. -P. 135-249.
- Korolkov, S.A. Generalized Harmonic Functions of Riemannian Manifolds with Ends/S.A. Korolkov, A.G. Losev//Mathematische Zeitschrift. -2012. -Vol. 272, iss. 1. -P. 459-472.


