Теоремы вложения для весовых функциональных пространств Бесова со смешанной нормой
Автор: Кулов Р.Д.
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 2 т.4, 2002 года.
Бесплатный доступ
Устанавливается теорема вложения весового функционального пространства $B^{\bar l}_{(\bar p)}\Epl n_{\bar\alpha,\theta}$ в весовое функциональное пространство $B^{\bar r}_{(\bar q)}\Epl m_{\bar\gamma,\theta_1}$.
Короткий адрес: https://sciup.org/14318048
IDR: 14318048 | УДК: 517.5
Текст научной статьи Теоремы вложения для весовых функциональных пространств Бесова со смешанной нормой
в ве-
Пусть Еп — п-мерное евклидово пространство точек ж = (жх, Жг,• • • , жп) и ( А ) = {ж Е Е" ,х^ > О (г = 1,2,... , п)}.
Предположим, что / (ж) произвольная достаточно гладкая функция, определенная в пространстве Еп , для которой
11/11
L№
(Л +
+ оо
/ I""dT”
о
+ оо
( I хД\Дхи_х О
+ оо
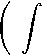
О
Р1
ж© d,X
• )
Рп
Рп
< ОО,
( +оо \ 6
[ ^||АгйП7||' + < оо,
п
11/11 , Z+^ ДДе W
= У 11/11 , z+p, <ОО, г = 1 (р) \ /
11/11
в'7 (р)
(Л
,а,6
11/11
чДЛ
^^.
^^. ,а
+ 11/11, £(р)
(Л
,й,У
Пространствами L^ ^Е ) -, СД ^Е ) й Q и В^ ^Е Д е называем замыкание достаточно гладких финитных функций в нормах (1), (3) и (4) соответственно.
Теорема 1. Пусть выполнены условия
-
(1) 1 < рг < % < ос (г = 1,2,... , m), pj > 1 (j = m + 1,... , п),
-
(2) I = (/i, /2, • • • Ц), где It > 0 (г = 1, 2,... , п), 1^ = Ц + Д, 1^ — наибольшая целая часть числа Ц, 0 < Д < 1, 1 < 0 < оо,
-
(3) m — натуральное число и m ^ п,
-
(4) й = Ду,п^,... ,пД, ^ ^ О Д = 1,2,... дт,),
© 2002 Кулов Р. Д.
-
(5) a = (щщг,. • .,«„), 7 = (71,72, • • • ,7m), ° < 77 < ^ (^ = 1, • • • ,m), a, > -1 U = m + 1,... ,n), n m / \ n
-
(6) E = 1 - E (i + „,Д - E ^ - 7 - E ^ > 0,
3 = 1 3 = 1 x 7 77 = 1
+n
(7)/eS',)(£ ).
Тогда при Imtl = ... = a„ = 0 верно D\‘ ...D^-J 6 Lm(B L и выполняется неравенство
н
■■■^"/11
нп5)
( +m X
VE )’7
<с||/||
(р)
(Л
,а,6
< Из интегрального представления В. П. Ильина и В. А. Солонникова [2] при ТГЦ = l^ k^ =2 имеем
+
н
■■■^"/11
НП5)
( +т х
VE )’7
С
< -- hw
„ h 11к vKi-tii
^У^Р» / д-(?)
1-1 о о о
hK j/(ж + у)П(у,/г)
о
( +m X ЧАЕ V
D^f^ +y)Ri(y,t,v)dt
, +m х
Е<АЕ ^^
п
= Jo + EJ- г = 1
Если применить соответствующую оценку для ядра, то будем иметь
Jo < ch
п пт
Е^)^-Е^+Е^
j = l 3 = 1 77 = 1
X
$+,lK m
\Иу)\ П^Г ж 7 = 1
—
21 ^3
п
сх
п Ул^у
7j=m + l
, +m x
E Применив обобщенное неравенство Минковского, неравенство Гёльдера и лемму Гу диева [3], получим п п т п т -Е(1+^^-Е^+Е^+Е^+Е^ Jo^ch 7=1 7=1 ^ " 7=1 -II/H + . Далее, h Щ,” г,”* Ji ^ с $рД / */Д^Р$№.^ — ж, ^ B^dt о ж о ( +171 7 LA^ )л < chE"b^ ж+17 X h «"< / \ [44 [И^и J у +AiJ о о /. _ HL A?(>'-n x ^ т Pi У/ — 21 ^ in. П ^" T)=mA-l ( +171 7 EAE )p ^ (применяем обобщенное неравенство Минковского, неравенство Гёльдера, лемму Гудиева) < C^ll/ll z + -Щ MpAe b“’9 * Из полученных оценок при /г = 1 имеем D?...D^f\\ + НД5)(я ),7 Теорема 2. Пусть выполнены условия: (1) 1 < Pi < qi< оо к = 1,2,... , m), Pj > (2)/ = (/1,/2,..П„),/г>0(г = 1,2,...,п), к U = т + 1,.. .дД ^^^^ ^^^^ = кР Pt, к — наибольшая целая часть числа к, 0 < Д ^ 1, ri = ri + ц, rt 1 < 0 < 9i< oo, наибольшая целая часть числа ri, 0 < Ti ^ 1, (3) m — натуральное число меньше либо равное п, (4) а = (qi,q2, • • • ,«Д, Р = (71,72, • • • ,7m), 0 < ^ < ^ U = 1, 2,... ,т) и аг > -1 (г = m + 1,... , п), (5)^ = i-EFE (^-4- Е ^+E^r+Er^-f">0(S = l,2,...,m), г = 1 J = 1 т/=т + 1 г = 1 з = 1 №ПеВ‘ГЦЕ у,. Тогда при жт + 1 = лт+2 = • • • = хп = 0 функция J^ принадлежит В^Е Д в1 и выполняется неравенство MW (+m. BbAE Wi baAe b“’e * < По определению имеем: II/II z+-4 BbAE M^ m = 11/11 (+m. P^MW-Tm. ■ На основании теоремы 1 при щ = v2 = ■ ■ ■ = vn = 0 справедливо неравенство 11/11 z+^ вдАЕ ) ,7 ВДМ ),a,6 * Исходя из определения нормы имеем: II/II r z+-4 ЛЛЕ W^ < hK= f dz zl + 6i0s O'-f ( +m X ЕАЕ Л (ОО Г dz J z^-+6iPs hKs ^® ^^» D? / Второе слагаемое оценивается просто: J2(S)^cb:v|| Z+mi ^^— = ^-^^11^/11 z 11 НЧ5)( / +™ \ ЕАЕ М = J^ + J^ * oo Ък= dz zi+6i0s 1 «I + т \ Е ) ^^» ,7 ^ (по теореме 1 при Z/i = Z/2 = • • • = ns_! = Z/s + i = • • • = Hn = 0, IVS = rs) < ch — Ks9s\\f\\ , z+n Л»ЛЕ b“-9 * Чтобы оценить рассмотрим интегральное представление В. П. Ильина и В. А. Солонникова при k^ = 2, m^ = Ц, ia1 = iv2 = • • • ^s-l — ^s + l — • • • Vu = О, vs = гs и представим его правую часть в виде суммы трех слагаемых: hK ^^» D? fM= ^7 //(ж+ у)П(у,/г)с?у о - 1 / К s vK tlKl — Уг Y,^ / ^ jdy / ^^D^Hac + ^RAy^t^^dt 1=1 0 00 Л / ^1/^ f^Q^jb + ^RA^W i = 1 ~1/Ks о 0 = Н1(ж, /г) — H2^x, h, z) — Н3(ж, h, z). ^^^^^^^^ ^^^^^^^^ ^^^^^^^^ Теперь имеем А'(|)д?/(ж) = /\2s^HAxJ^ - ^yAx,h,z^ - А2(|)я3(ж,/г,г). Следовательно, |к(^>:=/Ц ^ ЦА'(2)Я1(Ж’^1(5)(Д)д Далее + ^S (^ ^2 (ж, Я, ^ / +т\ + ЧДЕ ) ,7 ||л2(|)я3(Ж,М / +т \ ЬшД ) ,7 J*s) < dz ДДДД hKs\ + Г dz \U2fz\TTI , л01 ] ^1 + ^1лЛЛА2 ) ^2( ^ С(д)(5т),7 О/ + dz ДДДД ||А«(|)яз(жДл)|| __ т(8) | t(s) I t(s) Заметим, что As(|)^i(^)|| ,+™. < сг2||я2Я1(Ж,Л)|| +т , V27 ^^(^ ),7 Нд5)(я )-7 ||Ав(|)яз(яЛг ,+тх < ЬшД )Р cz P^3(®, h, г) +„ И Нд5)(я ) ^^» ,7 Оценим J^: J(s) < dz zH9i3s dz Д + (За —2)91 ||я2Я1(Ж, hK 9i P4^)-Z dz z^”V)3s —2)9i п^ДД I .f^ + уШуЛ^у о 9i ^ (оценим ядроП(у,/1) аналогично оценке в теореме 1 с небольшими изменениями) п m / \ п пт -Екз-К8Г8-Е(^-^- Е ^ + Е^ + Е^1 ^ ch j=1 j=1 ч=™ + 1 3 = 1 3 = 1 х ll/ll +„ . Аналогично, J^1< che-r=Ks J^ < ch£-TsKs ll/ll c1 (p) (ЕП),«,9 mp (^) * ,a,6 Из полученных оценок при h = 1 следует 11/11 z+™x buAe Wi <с||/|| +п . ▻ '/.Л^ И’6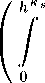
Список литературы Теоремы вложения для весовых функциональных пространств Бесова со смешанной нормой
- Соболев С. Л. Некоторые применения функционального анализа в математической физике.-Новосибирск: Изд-во СО АН СССР, 1962.-С. 64-67.
- Ильин В. П., Солонников В. А. О некоторых свойствах дифференцируемых функций многих переменных//Труды математического института им. В. А. Стеклова.-1962.-Т. 66.-С. 205-226.
- Гудиев А. Х. Нелинейные интегралы типа потенциала и их свойства//ДУ.-1966.-Т. 2, № 2.-С. 172-193.


