Теоретическая интерпретация темной материи в концепции реляционного статистического пространства-времени

При построении новой модели пространства-времени преодолевается рассогласование физического и математического аппарата квантовой механики и ОТО, что означает разработку теории для различных физических масштабов. На основе реляционной статистической модели пространства-времени в [1, 2] удается описывать динамику и кинематику с квантовыми проявлениями, а также воспроизводить гравитационные эффекты. Это потребовало введения новых представлений с рассмотрением специальных сумм по всем частицам (элементам) мира, что сопоставимо с обобщенным принципом Маха. Надо распространить эти представления на космологические масштабы, принимая во внимание потенциальные трудности ОТО в описании явлений для таких больших расстояний. Важная нынешняя проблема состоит в интерпретации темной материи и темной энергии.

Вопрос о смысле темной материи (ТМ) является одним из центральных для современной теории гравитации, общей теории относительности, космологии, поскольку с этим связаны многие следствия, важные и в практическом плане. Представления о темной материи складывалось постепенно. Первые гипотезы появились в 20-х годах XX века. Астрономы Джинс и Каптейн вычисляли плотность материи вблизи солнца, они также находили плотность всех звезд около плоскости Галактики. Джинс предсказал наличие двух темных звезд вблизи каждой видимой звезды, Оорт дополнил эти данные своими оценками. Позже были сделаны уверенные предсказания Цвикки в 30-х годах. В дальнейшем отчетливо наблюдалось рассогласование характера вращения звезд в спиральных галактиках с описанием по классической теории гравитации (Бэбкок). В 60-е годы в особенности усилиями В. Рубин получены оценки, близкие к современным. Сейчас о существовании ТМ и ее величине, составляющей около 26 % массы-энергии Вселенной, свидетельствует широкий спектр астрономических и космологических наблюдений. Но можно ли решить эту проблему путем поиска и наблюдения новых типов частиц или требуется модифицировать теоретические понятия и уравнения?

Эксперименты последнего десятилетия по прямому обнаружению частиц ТМ, взаимодействующих с обычной материей в наземной цел и-детекторе, не дали определенного результата [3-5]. Попытки найти слабо взаимодействующие массивные частицы (WIMP) не увенчались успехом. Например, авторы недавней работы [6] пишут, что при использовании модели сигнала нового канала WIMP-пион, частицы не обнаружены, что задает возможный новый верхний предел сечения взаимодействия.

С современной точки зрения необходимость введения концепции ТМ была вызвана в основном двумя проблемами: 1) наблюдаемыми некеплеровскими кривыми вращения спиральных галактик; 2) наличием дополнительной невидимой массы в скоплениях галактик, приводящей к наблюдаемому гравитационному ограничению кластеров (скоплениях), а также аномально большим гравитационным линзированием, создаваемым кластерами.

Наиболее важной (и исторически первой возникшей) представляется проблема адекватного объяснения неклассического вращения спиральных галактик. Среди различных экспериментальных результатов выделим некоторые, где приведены свидетельства в пользу альтернативы к по- иску неизвестных частиц скрытой темной материи. Например, в [7] сравниваются радиальные ускорения спиральных галактик: наблюдаемое, а также вычисленное по барионным массам. Наблюдаемое радиальное ускорение находится, исходя из видимой скорости звезд и расстояния до них от центра галактики. Соответственно ускорение с учетом только барионной материи можно найти, если вычислить гравитационные потенциалы с учетом плотности барионной материи из уравнения Пуассона. Затем определяется радиальное ускорение. При сопоставлении данных для большого числа галактик (153 галактики, 2693 экспериментальные точки) обнаружена существенная корреляция ускорений. Функция такой зависимости имеет вид

9obs = F (S b ar )

9bar

1 - exp(- ^g bar /з+)

Здесь g _obs — наблтодаемoe ускорение, gbar — ускорение, вычисленное по барионным массам. g+ — соответствующий нормировочный параметр, имеющий размерность ускорения. Данная зависимость показывает соотнесенность барионной и темной масс, поскольку наблюдаемое ускорение складывается из ускорений, связанных с темной и барионной материей. Поэтому можно предположить, что все определяется барионной материей. Полученное соотношение (описывающее наблюдаемую некеплеровскую зависимость вращения галактик) авторы в силу важности полученных результатов даже сравнивают с закономерностями, отраженными в кеплеровских законах.

В последнее время был достигнут ощутимый прогресс в обнаружении «потерянной массы» в кластерах (скоплениях), см. [8]. Авторы этой работы утверждают, что недостающие барионы находятся в крупномасштабных нитях (волокнах) в форме умеренно-горячей межгалактической среды. Наличие дополнительной массы в скоплениях галактик не подтверждается. В работе [9] при обработке изображения линзирования было показано, что пренебрежение рассеянным сигналом приводит к значительному завышению значения линзирующей массы.

Можно также отметить, что недавно были представлены кривые вращения галактик с сильным красным смещением и было ясно показано, что большая часть таких массивных галактик на самом деле является существенно барионными [10].

Поскольку концепция ТМ как субстанции неизвестных частиц подвергнута серьезному сомнению, то поиск новой теории представляется не только возможным, но и правильным направлением исследований. Но и независимо от экспериментальных данных само развитие теоретических представлений способно привести к такому же выводу. Один из способов разрешения проблемы с темной материей видится в изменении описания гравитации с помощью модифицированной ньютоновской динамики (MOND) [11]. Но все варианты MOND являются по сути эмпирическими теориями. В реляционных подходах Ю.С. Владимирова [12] (и нашем [13], где были получены первоначальные результаты) делается попытка описывать эффекты, связанные с темной материей, исходя из свойств пространства и времени. В предположении об изменении величины эффективного расстояния на больших масштабах удается объяснить ряд явлений.

Мы будем обсуждать здесь возможность теоретической интерпретации темной материи в рамках нашего реляционного статистического подхода.

1.    Модель реляционного статистического пространства-времени

Данная модель описана в различных публикациях, в частности в [1, 14-19], поэтому мы очень кратко представим ее основные положения и соотношения. Первое конструктивное предположение заключается в том, что в реляционной статистической модели пространства расстояние определяется конфигурацией масс в рассматриваемой системе элементов. Дискретная структура физического пространства прямо сопоставляется (на атомарных масштабах) с дискретной структурой материи, поскольку эталоны ——измерительные масштабные линейки состоят из атомов. Такая эталонная дискретная среда симметрично расположенных относительно друг друга элементов (атомов) задает модель измерительных масштабов, с которыми сопоставляется набор элементов изучаемой системы. Тем самым находится расстояние, отнесенное к заданному масштабу. Для расстояния между двумя элементами А и В по путям в дискретной среде (которую можно репрезентировать моделью соответствующего графа) между ними можно записать

Ь

^Г АВ = N~fg ( AB) .

• ¹    і =1

Здесь N1 — число прямых между двумя ^заданными элементами (в терминах теории гра ，( ] ) ов — прямую можно определить как маршрут с минимальным количеством вершин). Величина тпі ( ав ) соответствует i-ой прямой с суммарной массой (количеством элементов) на этом пути, равной m —все такие прямые имеют одинаковую длину. Сравнивая единицы расстояния и массы в операциональном подходе при определении пространства, мы конструируем модель безразмерного описания «масса-пространство». Статистический реляционный подход подразумевает, что непрерывная евклидова геометрия является некоторым пределом более общей дискретной геометрии, возникающей из простых геометрических образов. В такой статистической дискретной геометрии присутствует суммирование (осреднение) с использованием макроскопических инструментов для пространственных измерений. Можно также записать для приращения соответствующих масс и расстояния

Ь Ni dr = n £ 痴 J ¹ і =1

Множественность «прямых» (кратчайших маршрутов между двумя точками) характерна для малых масштабов, что и приводит к индетерминизму квантовой механики. На существенно больших расстояниях, как указано, возникает образ единственной прямой, поэтому для макроскопических масштабов можно записать dr = bdm.

Здесь расстояние может измеряться массой с соответствующим пересчетом в единицы обычной длины. Также и для неинфинитезимальных расстояний, которые будут фигурировать, например, в величинах ньютоновского потенциала, можно записать r = bm.

Связь между массой и расстоянием (длиной) линейная, поскольку может быть реализована на простом графе, соответствующем набору частиц в дискретной среде идеального прибора -измерительной линейки. В такой модели есть минимальное расстояние, ассоциируемое с одной частицей. Так что можно записать:

% = bme, где % — величина частицы (атома, электрона), me — масса атома, и размерный множитель b выражается через фундаментальные константы при рассмотрения соответствия данной модели с соотношениями квантовой механики:

b =方/(m2 с), где 方—постоянная Планка.

Время вводится при уже построенном пространстве. Поэтому второе конструктивное предположение заключается в возможной измерительной связи времени и пространства. Задается «идеальный фотоаппарат», позволяющий получать «фотографии» всех частиц. Конструируется система отсчета с декартовой системой координат. Определяются радиусы-векторы всех частиц по

«фотографиям» и находится точка в соответствующем конфигурационном пространстве, определяющая момент времени

R = {ri,...,门V}, где N — число частіш, (элементов) в системе.

По изменениям моментов времени dR = {dri,...,drv }, вводится приращение времени, определяемого как среднеквадратичное от изменения всех пространственных координат в «фотографиях», соответствующих различным моментам времени:

• 2    V        1V

2.    Получение выражения для гравитационного потенциала в модели и связь с космологическими совпадениями

^{dT 2} = N £ (也一 _N E dr )2.

2=1           J=1

Множитель q = 1/c, где с — скорость света, определяет связь между величинами размерности пространства и времени.

В предлагаемом реляционном подходе, как показано ранее в [1, 2, 19], метрика пространства-времени зависит от распределения частиц. При «сгущении» в массивных телах по сравнению с фоновыми значениями измерительной среды происходит искривление траектории частиц. В частности, воспроизводятся эффекты линзирования.

В нашем подходе фактически выводится гравитационный потенциал, что напрямую связано с тем, что изменение распределения масс соотносится и с изменением расстояния. Вид гравитационного потенциала с обратной пропорциональностью расстоянию от гравитирующего тела до рассматриваемого связан с характером измерения расстояния с помощью масштабной линейки, при котором длина оказывается пропорциональной массе. Так что отношение массы к расстоянию -безразмерная величина. Вывод выражения для потенциала основан, по сути, на математических закономерностях и соответствующих связях в моделях физических приборов.

Вид традиционного гравитационного потенциала может быть получен при сопоставлении двух сумм безразмерных величин, см. [18, 19]. Предполагаемая величина ньютоновского потенциала представляет собой сумму отношений масс тел к расстояниям до них от пробного тела (учитывая измерительную эквивалентность расстояния и массы). Она сравнивается в согласии с суммой нормированных на квадрат скорости света квадратов скоростей частиц, образующих массивное тело. Эта сумма отвечает за замедление времени по сравнению с временем, определяемым при равномерном распределении частиц в некотором статистическом выражении. В пределе такая сумма выражает отношение квадратов скоростей к квадрату скорости света для всех элементов мира. Члены в ней порядка единицы, поскольку проводится нормировка на квадрат скорости света (в принятом способе определения скорости по фотографиям, определяемым в точке наблюдателя, средняя скорость равна скорости света). Сопоставление таких безразмерных сумм и приводит к известной форме гравитационного ньютоновского потенциала.

Поясним приведенные выше краткие утверждения количественными соотношениями. Все члены суммы будут представлять собой безразмерные величины, образованные отношением массы элемента к расстоянию от точки наблюдения, выраженную тоже в единицах массы. Данную сумму в согласии с законом больших чисел можно сопоставить с упомянутой выше суммой безразмерных нормированных квадратов скоростей. С простыми допущениями теории вероятностей получаем, что относительные отличия двух указанных сумм составляют статистическую величину, равную

(N)^-1/2. где N — число (фундаментальных, элементарных частіш, в мире. Часто эту величину полагают равной числу Эддингтона N = 1080. В данной глобальной сумме фигурирует отношений масс объектов к расстоянию до пробного (1-го) тела. Причем для шара при равномерном распределении частиц основной вклад в такую сумму будут вносить элементы, сосредоточенные вблизи сферы порядка радиуса Метагалактики (мира) R, более точные оценки должны дать некоторую эффективную часть радиуса. Поэтому можно записать

ГІ2 〜 R.

Множитель А связывает величину радиуса мира с характерной микроскопической величиной, например, размерами атома (радиусом электрона):

R = А%.                             ⑴

Учитывая указанную связь между расстоянием и массой с помощью множителя 6, получаем, что можно вынести в знаменателе комплекс АЬ:

riz = АЬт _{1 г} .

⑵

⑶

Тогда для искомой суммы гравитационного потенциала с учетом (1) и (2) имеем

NN   N

_   工^ ^те _ 厂工^ ^те _ G 、^ ^те

侮, ・ ⁿ = -       = -     аьm^ = - aь*m1?

Z=2            Z=2                  Z=2

Вывод гравитационного потенциала опирается на соотношения теории вероятностей, где сравниваются суммы безразмерных случайных величин порядка единицы

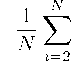
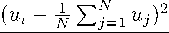
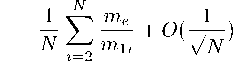
Здесь полагается, что присутствуют случайные величины одного порядка, а именно

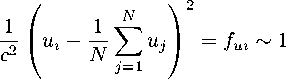
те mi?

f mi 〜 ¹.

Физический смысл в такие математические соотношения вносится с помощью комбинаций мировых констант, что задает размерные физические величины. С учетом вышеприведенного ожидаемого вида потенциала (3), пренебрегая малой вероятностной ошибкой, получаем

1 ур (li - N e 上 1 出 ) ² . G f m_e

N 乙     с2       АЬс2 乙 тц i=2                                     i=2 1z

Отсюда

G _ 1

— ： --=—

АЬс2   N или

GN _ GNm _e

⑷

Ьс ²      С²Ге

Правильность описания подтверждается выводом из этих выражений так называемых космологических совпадений (впервые отмеченных Вейлем), т. е. соотношений, где связываются величины микро- и макромира. Получение таких известных эмпирических соотношений, исходя из статистических глобальных космологических выражений, следующих из положений реляционной модели пространства и времени, можно рассматривать как своеобразную манифестацию принципа Маха.

Если сопоставить получающийся множитель перед суммой отношений масс к расстояниям с множителем в выражении для гравитационного ньютоновского потенциала множителем, то выводим первое важное соотношение, которое показывает, что радиус мира близок к гравитационному радиусу Вселенной. Принимая во внимание (1) и (4), получаем

_R__Ar _ GN^e 〜2GNm_e _ 2GM _ 冗

Второе соотношение характеризует отношение радиуса Метагалактики и радиуса электрона. Оно получается, если исходить из условия динамического равновесия любого атома в мире. Для этого требуется, чтобы электрический потенциал, например, электрона соответствовал суммарному при взаимодействии всех остальных протонов и электронов во Вселенной. Сравнивая порядки потенциала одного электрона с суммарным потенциалом всех разноименных зарядов во Вселенной, получаем а = Nn.

Третье соотношение получается при сопоставлении суммарного воздействия дипольных моментов всех атомарных систем Вселенной с суммарной гравитационной силой Вселенной. Это соотношение показывает связь характерной величины электромагнитного взаимодействия с аналогичной характерной величиной гравитационного взаимодействия в2

Gm 2

Nn 〜 io⁴⁰.

3.    Важная оценка для интерпретации темной материи

В настоящей работе с помощью подхода для построения реляционного статистического пространства-времени предлагается конструктивная модель, в которой на основе принятого соответствия расстояния и конфигурации масс удается объяснить галактическое проявления темной материи.

Чтобы сопоставление различных членов имело смысл, они должны быть одного порядка. Поэтому рассматриваемая «плотность», т.е. отношение массы к расстоянию должна быть одного порядка в различных физических условиях, отношение массы к расстоянию безразмерно, данную величину можно назвать безразмерной плотностью, (с возможным выделением при необходимости соответствующего размерного множителя, составленного из фундаментальных констант). Надо будет определять значения данной безразмерной плотности при оценке значения темной материи.

Заметим, что реляционный подход к природе пространства-времени и физических взаимодействий, развиваемый в [12], позволяет использовать некоторые соображения Рашевского (и Рваче-ва). Поскольку пространство имеет вторичный характер по отношению к объектам микромира, может оказаться так, что расстояния между астрофизическими объектами (те, что входят в закон всемирного тяготения и формулу центростремительного ускорения) отличаются от значений, получаемых нами в наблюдениях с Земли. На этом основана предлагаемая в этой работе интерпретация MOND, которую можно условно назвать теорией с «модифицированным расстоянием» (“modified distance^^). Причем было получено, что эффективная масса примерно в 6-10 раз больше видимой материи.

В нашем реляционном статистическом методе не делается гипотетических (хотя и продуктивных) предположений об изменении фактических физических длин при возрастании расстояний до космологических масштабов. Мы исходим из анализа измерительных процедур измерения расстояния с учетом структуры линеек. При этом распределение реальных частиц в мире сопоставляется с предельно однородной структурой распределения атомов в эталонах для определения расстояний. Выражение для гравитационного потенциала получается фактически из математических закономерностей. Такая операциональная эквивалентность между расстоянием и конфигурацией масс, а также между временем и сменой пространственных картин приводит к безразмерным уравнениям, где связь с физическим смыслом осуществляется с помощью соответствующих комбинаций мировых констант. В результате ньютоновский потенциал выводится из данных постулируемых соотношений измерительных эквивалентностей между массой, расстоянием и временем. Величины расстояния, фигурирующие в выражениях для потенциала могут быть сопоставлены с величинами, измеряемыми по заданным эталонам в случае однородного распределения «той же» плотности, что и в данных эталонах масштабных линеек. В случае нарушения однородности реального распределения частиц (появление массивных тел, например планет, звезд, галактик) отличия от однородного распределения в измерительном приборе для расстояния приводит к известным эффектам ОТО. При изменении плотности распределения «частиц» по сравнением с заданным эталоном в масштабной линейке, что определяется предельной возможной плотностью по всем элементам Метагалактики, возникают эффекты, которые можно трактовать, как проявление темной материи,-здесь это следствие самой теоретической модели, а не влияние новых неизвестных частиц. Здесь важно еще раз подчеркнуть, что все определяется отмеченной выше плотностью безразмерного расстояния (или массы).

Можно дать оценку эффективного расстояния для галактики по сравнению с обычным расстоянием, которое присутствует в традиционном вычислении. Но оно оказывается заниженной, что соответствует проявлению темной материи. Число нуклонов, приходящееся на единицу объема для дискретной однородной измерительной среды

^{U Mes} — (1028)3

Здесь общее количество нуклонов в Метагалактике (число Эддингтона) равно, как уже указывалось. N = 1080- радиус Метагалактики со гласно ігзвестпым данным 10²⁸ см. Так что ра ： змериость приведенной в оценке величины 1 /(ст)³. Число нуклонов, приходящееся на единицу объема для галактической среды (в Метагалактике 2 • 10¹² галактик), значит

1080          1

2 • 1012(1023)3 = 210 1.

Тогда отношение обратных значений эффективного и обычного расстояний, а значит и отношение полной массы, участвующей в гравитационном взаимодействии (барионной + темной) к барионной, равно

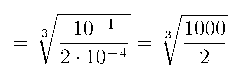
Что соответствует примерно реальному соотношению (с учетом того, что в данной первоначальной оценки фигурируют величины многих порядков).

Таким образом, показано, что величина расстояния, которая должна фигурировать в знаменателе, чтобы суммарный глобальный гравитационный потенциал остался прежним, существенно превышает обычную. Но подставляют именно обычную величину. Поэтому сумма завышается, что интерпретируют как проявление темной материи.

Заключение

В работе показано, что подход, основанный на построении реляционного статистического пространства-времени, позволяет не только описать квантовые и гравитационные эффекты ОТО, что было показано ранее, но объяснить и явления, связанные с темной материи. Здесь устанавливается новая связь между массой, временем и пространством. В ОТО искривленность пространства-времени в присутствии тяготеющих масс проявляется как дифференциальное свойство гиперповерхностей на макроскопических (по сравнению с атомарными) масштабами. Такие же свойства определяются и в реляционной статистической модели, но здесь они основаны на операциональной связи между массой и расстоянием. Такая связь позволяет на космологических масштабах описывать эффекты, которые ассоциируются с проявлением темной материи. В настоящей работе пока получена общая оценка, позволяющая найти отношение темной и барионной материи к барионной материи в целом. Такая величина показывает, что с помощью развиваемой реляционной модели пространства-времени можно, в принципе, описывать эффекты, связанные с темной материей. Но, конечно, подробное описание, например, вращение отдельной спиральной галактики требуют более точных конкретных оценок.