Теоретическая модель режима фазового запрета для волны разностной частоты нелинейного излучателя звука

Электронный журнал «Техническая акустика»

Под режимом фазового запрета понимаются такие условия для амплитудных, фазовых и частотных соотношений в спектре излучаемой регулярной волны конечной амплитуды, при которых в процессе нелинейного взаимодействия оказываются перекрытыми один или несколько возможных каналов оттока энергии из накачки во вторичные волны. Подобное влияние амплитудно-фазовых соотношений на волновые процессы в квадратично-нелинейных средах без дисперсии возможны для нескольких различных типов исходных волн. Одним из таких случаев является узкополосная трехчастотная волна накачки нелинейного акустического излучателя (НАИ) с симметричным частотным спектром (ω0 - Ω , ω0 , ω0 + Ω ), генерирующая в среде бигармоническую волну разностной частоты (ВРЧ) с частотами Ω и 2Ω . Существенно, что эти низкочастотные вторичные волны качественно отличаются между собой по характеру зависимости от начальных амплитудно-фазовых соотношений в спектре накачки.

Поскольку 2-я гармоника ВРЧ (2 Q ) возникает в результате взаимодействия боковых составляющих спектра ( го ₀ -Q , го ₀ + Q ), то фазовые соотношения первичных волн способны повлиять лишь на ее начальную фазу. Случай 1-й гармоники ВРЧ ( Q ) отличается тем, что эта волна состоит фактически из двух равночастотных компонент, образовавшихся в процессе синхронного взаимодействия центральной гармоники первичного спектра ( w ₀) с нижней ( го ₀ -Q ) и верхней ( го ₀ +Q ) частотами накачки. При определенных амплитудно-фазовых соотношениях в спектре накачки может наступить условие, когда амплитуды этих компонент окажутся равными, а фазы противоположными. Тогда наступает акустическое “короткое замыкание” вторичных нелинейных источников, генерирующих компоненты с частотами Q , приводящее к прекращению образования 1-й ВРЧ.

Интерес к режиму фазового запрета 1-й ВРЧ НАИ обусловлен открывающимися возможностями его практического использования. В частности, это может быть диагностика неоднородностей среды (газовые пузырьки, гидродинамические возмущения, температурные и структурные неоднородности) [1, 2], обнаружение объектов вблизи и на границах раздела (морское дно, граница вода-воздух, дефекты поверхности), контроль неровностей границ (микрорельеф дна, поверхностное волнение, шероховатость твердых тел), уменьшение нелинейного затухания [3], акустические измерения и др. Широкое продвижение в практику методов акустической диагностики, использующих режим фазового запрета вторичных волн, в значительной степени сдерживается ограниченным количеством сведений по данному вопросу. Так, в частности, имеющиеся экспериментальные результаты [1–3] не находят своего объяснения в рамках плосковолновой и других одномерных моделей НАИ [4, 5]. Причинами расхождений является частотно-зависимый характер диссипации и дифракционных процессов в пучке, приводящий к изменению амплитудных и фазовых соотношений в излученной многочастотной волне накачки. Целью данной работы является разработка теоретической модели НАИ, описывающей процесс генерации 1-й ВРЧ трехчастотной накачкой с произвольными амплитудно-фазовыми соотношениями при учете диссипации и дифракции волн.

1. АКУСТИЧЕСКОЕ ПОЛЕ ДИФРАГИРУЮЩЕЙ ВОЛНЫ НАКАЧКИ

Воспользуемся аналитическими решениями уравнения Хохлова-Заболотской-Кузнецова (ХЗК) [5]

д д p г д p b д ² p дт д x р ₀ c 0 Р дт 2 p ₀ c 0 дт ²

= 2 ^Ai Р ^,

которые позволяют учесть диссипативное затухание, дифракцию первичных волн (накачки) и генерируемых ими в среде вторичных волн. Здесь p — звуковое давление;

c 0 , s и p ₀ — скорость звука, нелинейный акустический параметр и плотность среды; b — диссипативный коэффициент среды; т = ( t - x/c ₀ ) — время в сопровождающей системе координат; Д _х = ( б ² / д y 1 + д ² / д у 2) — лапласиан по поперечным координатам.

Рассмотрение теоретической модели НАИ для ВРЧ проведем на примере звуковых пучков волн накачки с гауссовым поперечным распределением амплитуды. Гауссов закон для поперечного распределения удобен тем, что позволяет получить общие решения для первичных и вторичных волн через достаточно простые функции. Граничное условие в цилиндрической системе координат для осесимметричных пучков волн накачки с гауссовым амплитудным и равномерным фазовым распределениями на поверхности плоского излучателя имеет вид:

P n ^{( t} , r , x = ^{0 )} = P о • exp ^(- r²/a ² ) • cos ⁽w n • t + ф n о ) ,

где a — радиус излучателя; го _n — частоты первичных волн; n = ( 1, 2, 3 ) ; P _0n и ф _{0 n} — начальные ( x = 0 ) значения амплитуд и фаз волн. Здесь r и х — поперечная и продольная (осевая) координаты; го 1 го H = ( го ₀ - Q ) , го ₂ го ,, и го ₃ го B = ( го ₀ +Q ) — нижняя боковая, центральная и верхняя боковая частоты спектра первичной волны. В дальнейшем индексам n = ( 1, 2, з ) соответствуют индексы “H”, “0” и “B”, связанные с введенными обозначениями частот го H ₀ B .

Решение уравнения ХЗК в первом приближении для граничного условия (1) дает следующие выражения для пространственных распределений комплексных амплитуд волн накачки [5]:

^P , ^{( r} , ^{х ) =} , P 0 n,, • exP г г д n

\

\

a ² 1 - ix/l _{д n}

a n x

= ^P n ^{( r} , ^x ) • exp [ / [ ф n ^{( r} , ^x ) + Ф 0 n ]] ,

где l _{д n} = k _n a 2/ 2 = го _n a 2/ 2c ₀ — длина зоны дифракции волн накачки; k_n =го Jc ₀; ф _n ( r , x ) — пространственные набеги фаз каждой из волн, обусловленные дифракцией пучка; i = 4- 1 ; P _{0 n} = P_0n • exp ( i y _{0 n} ) — комплексные амплитуды первичных волн на поверхности излучателя; P_n ( r , x ) — пространственные распределения амплитуд волн накачки, обусловленные дифракцией и диссипацией. Для случая трехчастотной накачки удобно ввести безразмерный частотный параметр Ф = го ₀ /Q , тогда параметры, характеризующие влияние дифракционных и диссипативных процессов, запишутся:

гоH = го0 (1 - 1 ф) ;    гоB = го0 (1 + 1 ф);     1 д0 = a го0/2c0;, _a4 _a4Г,f,Y , _a4 _, f, i Y lдH      т T I 1 Л I lд01 1 « I ; lдB      ,         lд01 1 + - I ;

2c0     2c0 ^   Ф J     ^   Ф J         2c0      ^ Ф J                     (3)

^{2 p} 0 ^c 0

2 P 0 c 0    0 1 Ф

B

2 p 0 c 0    0 1 Ф

С учетом (2) выражения для комплексных амплитуд исходных волн принимают вид:

PH (r, z ) =

P 01

1 - izФ/(Ф -1)

exp

a

1 - iz Ф/(Ф-1) “ 0 [' Ф    ‘’ 0

P 0 ^{( r} . ^z ) =

p

1 - iz

( exp

к

2 / 2 r ² a ²

1 - iz

-

^a о ^zl а о

•

P B ^{( r} , ^z ) =

03        _exp

1 - iz Ф/(Ф + 1)

2 / 2

r ² a ²

1 - i z Ф/ ( Ф + 1 )

- a о

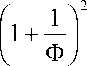
zl z до

где z = x/l _{3 0}. Действительные амплитуды и фазы при этом описываются формулами:

PH (r,z ) =

^P 01

71 + z ² Ф ² /(Ф- 1 ) ²

exp

r²1 a²                Г, 1 1 ² ,

0)1 1I zl;

1 + z ² Ф² /(Ф- 1 ) ^{2    0} к ф7

< \ Г z Ф 1 r2

Ф H(r,z ) = arctgl;;—tI—2 кФ-1 7 a

z Ф/ ( Ф - 1 )

1 + z ²Ф ²/ ( Ф- 1 ) ^{2 ;}

P o ^{( r} , ^z ) =

P ₀₂

J 1 + z²

r exp

к

r ² a ²

1 + z²

-

Фо(r,z)=arctg(z)- rr • r^r; a 1 + z

A

^a 0 ^zl а 0

;

^P b ^{( r} , ^{z ) =}

1 + z ²Ф ² /(Ф + 1 ) 2

r²/a²               Д ,1 1² ,

----z——77----- 7—a ₍₁l 1 +— I zl-

1 + z 2Ф2/(Ф +1)2    0 к ф7/ \      , Г z ФФB (r,z) = arctgl Ф+1

z Ф/ ( Ф + 1 )

1 + z ²Ф ² /( Ф + 1 ) ² ’

Условия проводившегося эксперимента (пресная вода) и последующие расчеты с использованием полученных формул соответствуют следующим параметрам:

f 2 = f ₀ = a ₂/2 n = 1400 ( кГц ) ; a = 9 ( мм ) ; b = 4,27 • 10 ^-3 ( кг / м • с ) ;

F = Q/ 2 п = 50, 80, 100, 120, 150 ( кГц ) .

М r,x)

£1Р Р i ^2—01—02

2 Ро c 03

• e “ " ^x X

X

J ‘

exp

2 r ²

• a2 1 - i (x

^^^^a

1 + ix L _g/⁽ l _{g l} • l ₃ 2 )

x )/ L a + x ^{( i 2} L a / ^l a i ^l a 2 + xl ^l a i ¹ 8 2 ) _

1 — i ( x — x ')/ L _s + x 'ii 2 L _s /l ₃ 1 l _s 2

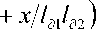
• dx' ,

где l 31 = a 2w1/2 c 0; ld 2 = a 2o2/2 c 0; L 3= a2 Q/ 4 c 0; Q or o,; a = a1 + a 2 — an; a1 = bo2 /2p0c0; a2 = bo2 /2p0c0 ; aQ = bQ2/2p0c0.

*

Здесь P₀₁ — величина, комплексно сопряженная с P ₀₁; L ₃ — протяженность области дифракции ВРЧ; Q — разностная частота; a ₁, a ₂ и a_Q — коэффициенты затухания волн накачки и ВРЧ.

• 3.    ГЕНЕРАЦИЯ ПЕРВОЙ ГАРМОНИКИ ВОЛНЫ РАЗНОСТНОЙ ЧАСТОТЫ ДИФРАГИРУЮЩЕЙ ТРЕХЧАСТОТНОЙ НАКАЧКОЙ В СРЕДЕ С ДИССИПАЦИЕЙ

Первая гармоника ВРЧ (1-я ВРЧ) и волна суммарной частоты (ВСЧ), образующиеся при взаимодействии трехчастотной накачки, в приближении малой нелинейности являются двухкомпонентными вторичными волнами, поскольку состоят из двух волн одинаковой частоты, распространяющихся в одном направлении синхронно и коллинеарно, рис. 1.

Ваты накачки

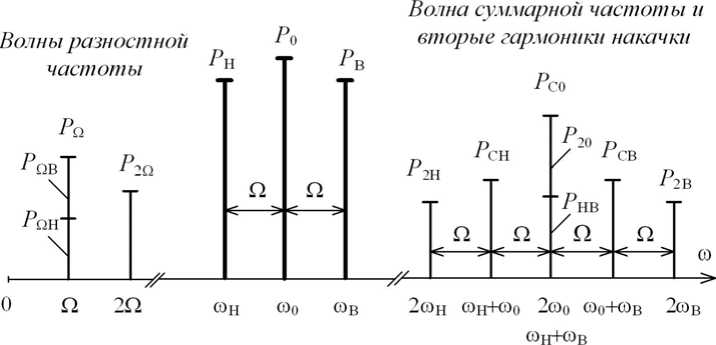
Рис. 1. Спектры трехчастотной накачки и генерируемых ею вторичных волн (второе приближение)

взаимодействии первичных волн PH и P0, а волна PoB обязана своим появлением взаимодействию между P0 и PB . Тогда для получения выражений, описывающих каждую из рассматриваемых вторичных волн, достаточно воспользоваться выражением (6) с учетом индексов первичных волн. В результате получаем

*

^а о ¹ до z L

Ф ² J

. £И0 Ph Ро ,       । i э 0 з ° lдо • exP| 2ро c оф

z

X J exp - ^2a о l

0       _

- I ^Ф-1 1 _z' ^{д о} l Ф J

exp( - 2 r 2 ------7—

1    ^H 1 - i 2 ® ( z -

1 + iz '/ 2 ( Ф - 1 ) _______________ '

z ') + z'[i/ ( Ф - 1 ) + z Ф/( Ф - 1 ) ] /

1 - i 2 Ф ( z - z ') + z'[i /(Ф - 1 ) + z Ф/ ( Ф - 1 ) ]

• dz' ;

*

- z X . rm, P о P_B |

P B ⁽ r H , ^z ) = i _o^о 3 * l д о • ^ex P | 2Po c 0^Ф          '

^a о l д о ^z L

Ф ² J

z

X J exp - 2 a о l о _

- I ^{Ф+ 1} 1 _z' ^{д о} l Ф J

2 r 2______________1 + iz 7 2(Ф +1)_____________\ rH 1 - i 2Ф(z - z') + z '[i/ (Ф +1) + z Ф/(Ф +1)]/

1 - i 2 Ф ( z - z ') + z '[ i /(Ф + 1 ) + z Ф/ ( Ф + 1 ) ]

• dz' ,

где   r _H = r/a ;   a _{( H} ) =а _о + a _H -a _o = 2 a _о ( 1 - 1/ Ф ) ;   a _{( B} ) =a _B +a _о -a _o = 2 a _о ( 1 + 1/ Ф ) ;

L _д = l _до/ 2 Ф ; a _o = a _о/Ф ² . Здесь согласно введенным обозначениям для начальных

«                     •                 •                   •                       •                  • амплитуд волн накачки справедливы соотношения PH = P)1, PB = Pоз и Pо = Pо2 .

Для упрощения последующих преобразований полученные выражения (8) и (9) запишем в обобщенном виде:

*

P H ^{( r} H ’ ^z ) = ^{Ph P} 0 D H ^{( r} H ’^z ) ^;

*

P B ^{( r} H , ^z ) = ^{P о P} B D B ^{( r} H , ^z ) ,                                                               ⁽ )

где D _H ( r _H , z ) и D _B ( r _H , z ) — множители, отражающие пространственные распределения амплитуд и фаз компонент 1-й ВРЧ, учитывающие нелинейные, дифракционные и диссипативные процессы.

Запишем трехчастотное возмущение для накачки (1) на поверхности излучателя (z = о) в вещественной форме p (1)(t, rH,z = о)= PH • cos(wHt + фH)+ Pо • cos(ю01 + фо ) + PB • cos(mBt + ФB).             (12)

Тогда, приняв условие аддитивности полей двух компонент, выражение для 1-й ВРЧ в произвольной точке пространства можно представить в виде pО (t, rH , z) = POH (rH ,z) • cos(ot - kОzlдо + Фо - ФH ) +

⁺ P B ^{( r} H , ^z ) • ^{cos (o} t ^- k О ^zl д о +Ф B ^-Ф о ) =                                               (13)

= PHPDH (rH ,z) • cos(ot - kОzlдо + 0 - Ро ) + PPBDB (rH ,z) • cos(ot - kОzlдо + 0 + Ро ) , где k о = О/ c о; ф b - Фо =0 + Ро;   Фо- фн = 0 - Ро;

⁰ = ⁽Ф B ^-Ф н )/ 2;    Р о =⁽Ф н ⁺Ф в )/^{2 -}Ф о -

Здесь ф H , ф ₀ и ф B — начальные фазы ( z = 0 ) волн накачки; р ₀ — начальное значение фазового инварианта, отражающего фазовую структуру трехчастотного колебания [6]. Нетрудно убедиться, что в плоской трехчастотной волне малой амплитуды величина в не зависит от времени и проходимого расстояния. В выражениях D_H ( r_H , z ) и D B ( r_H, z ) разделим амплитудную и фазовую составляющие:

^D H ( r H , ^Z ) = ^D H ( r H , ^Z ) ‘ ^exp [ / ^ф я н ( ^r _H , z ^{)] ;}

D^ B (rH , Z ) = DB (rH ,z ) • expt Фя B (rH ,z )], где DH (rH, z) и DB (rH, z) — модули пространственных множителей; фоH (rH, z) и Фо B (rH, z) — дифракционные набеги фаз у компонент 1-й ВРЧ. Учитывая (15) и (16), выражение (13) можно переписать в вещественном виде p я (t, Гн,z) = P0 { KhDh (rH,z) • cos[o t — k о zl а о + 0 — Po + фо h (rH,z)] +

+ K B D B ^{( r} H , ^z ) • ^{cos [} ° t ^- k я ^zl 3 о ^{+ 0 +} P o +Ф я B ^{( r} H , ^{z )]} } =

= P 2 V( K h D h ) 2 + ( K b D b ) 2 + 2 K h K b D h D b cos [ 2 p o + Дф я ( r H , z ) ] x

X cos[o t - к я l a 0z + ая( rH,z)], где Kh = PH /Po ; KB = PB IPo ; Дфя (rH , z) = фяB (rH , z) — фяH (rH , z) •

Величину ая( rH, z) запишем в виде суммы ая( rH,z ) = 0 + a1 (rH,z), где

(r 7)= KbDb(Гн,z)sin(Фяв +Po) + KHDH (rH ,z)sin(ФянP tg a 1 ( г h , z) =          к \ к \             к \ к\ •

K B D B ^{( r} H , ^z ) ^{cos (}Ф я в +P o ^{) +} K H D H ^{( r} H , ^z ) ^{cos (}Ф я н ^— P o )

Тогда выражение (17) для 1-й ВРЧ принимает окончательный вид p я (t, Гн , z) = P JKHDj+KD)^^x

x cos[я t — knLnz + 0 + a, (r„, z)].

L         я do              1 \ H ~ 7J

Полученные выражения для амплитуды и фазы 1-й ВРЧ можно значительно упростить, если принять во внимание, что при использовании узкополосной накачки ( я <<« ) справедливы следующие соотношения:

Ф я H ^{( Г} н , ^z ) ^ Ф я в ^{( Г} н , ^z ) ;

^D H ^{( r} H , ^z ) — ^D B ^{( r} H , ^z ) •

Очевидно, что при Ф > да частоты накачки настолько мало отличаются между собой, что можно говорить для них о равенстве дифракционных и диссипативных процессов. В результате пространственные распределения акустических полей вторичных волн Р _п H и Р _п в с достаточной для практики точностью также можно считать равными.

При условии (20) соотношение (18) можно переписать в виде а1 (rH , z) - Фон (rH , z) + arctg

K B D B ( ^r H , ^z ) K H D H ( ^r H , ^z ) , K_BD_B ( r_H , z ) + K_HD_H ( r_H , z ) BBH   HHH

tg P 0

Ф о H ^{( r} H , ^{z )+}Y 1 ^{( r} H , ^z ) •

Если принять, что наряду с (20) выполняется и равенство (21), тогда в выражении для фазы 1-й ВРЧ (22) исчезает зависимость от дифракционных изменений амплитуд первичных волн:

« 1 ^{( r} H ,^z ) ~ Ф^ ^{( r} H , ^z ) ⁺ arctg

V

K B - KL 1

K_B + K_H )

BH

tg p

= ^ф Q H ^{( r} H , ^{z ) +} Y i ■

Согласно (23) использование узкополосной накачки приводит к тому, что фазовая структура поля 1-й ВРЧ с точностью до постоянного слагаемого у 1 повторяет пространственное распределение фазы отдельно взятой компоненты: ф_{п H} ( r_H , z ) или Ф_п B ( r_H , z ) ■ Величина сдвига фазы у 1 не зависит от пространственной координаты и определяется только отношением начальных амплитуд боковых составляющих спектра накачки P H /Р_в = K H / К_в и начальной величиной фазового инварианта Р ₀.

Заметим, что второе слагаемое в выражении (23) принимает конечное значение в случае асимметрии амплитудного ( K H ^ К_в ) и фазового ( Р ₀ / 0) спектров накачки. Напротив, в случае K H = К_в равенство у 1 = 0 выполняется вне зависимости от величины Р ₀, и пространственные набеги фазы 1-й ВРЧ а 1 ( r_H , z ) определяются дифракционными фазовыми набегами в отдельно взятой ее компоненте:

^а 1 ^{( r} H , ^z ) ~^ф п H ^{( r} H , ^{z )—ф} п в ^{( r} H , ^z ) ■ (24)

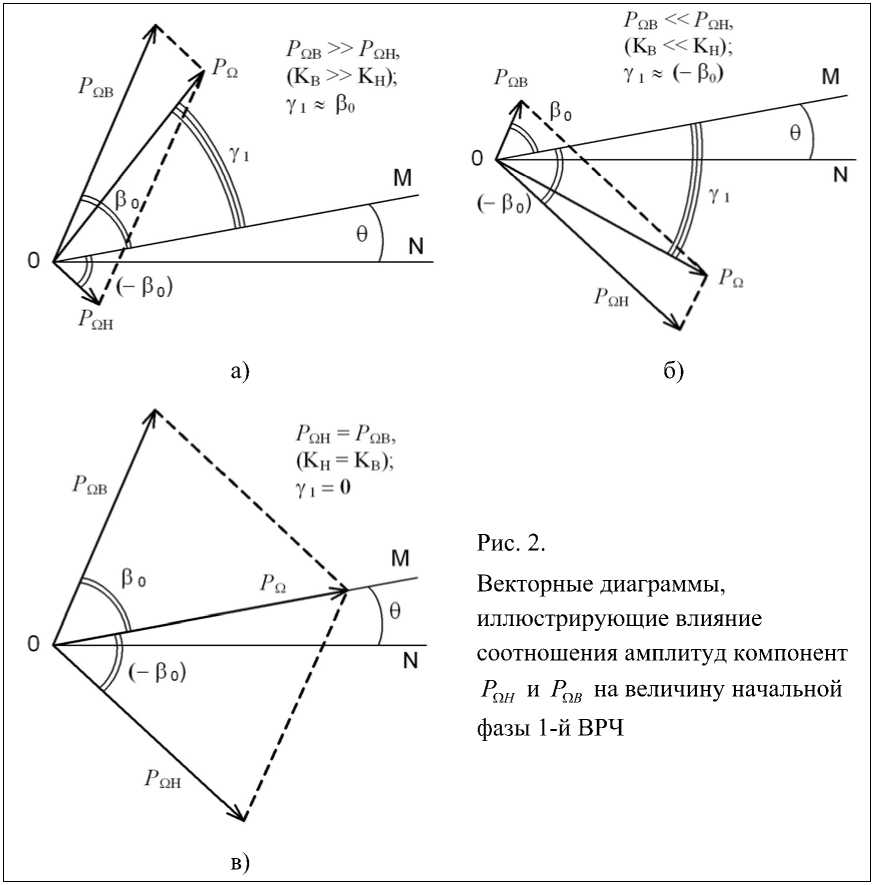
Механизм появления дополнительного сдвига фазы у 1 проиллюстрирован на примере векторных диаграмм, отражающих процесс формирования 1-й ВРЧ входящими в ее состав компонентами Р _п H и Р _{п в} , рис. 2. Поскольку Р о H ~ ^{( P} H ^P 0 = ^P 02 ^K H ) ^{и Р} о в ~ ^{( Р} в ^Р 0 = ^Р 0^{2 К} в ), ^{то в} случае ^K H = ^К в длины векторов ^Р п H ^и Р _{п в} также равны, а их сумма (вектор Р _п ) при любом значении фазового инварианта сохраняет свое направление неизменным (угол 0 ), рис. 2-в. При K H ^ К_в неравенство амплитуд компонент Р _п H и Р _{п в} приводит к появлению дополнительного поворота вектора Р _п на угол у 1 , рис. 2-а и рис. 2-б. Видно, что в случае К_в >>  K H имеет место Y 1 > в ₀, а при К_в <<  K H получаем у 1 ^ ( - в ₀ ) .

Учтем соотношения (20) и (21) в отношении амплитуды 1-й ВРЧ, что приводит к следующему выражению:

P ( r_H , z ) « P ² D_H ( r_H , z ) JK2 + K 2 + 2 K_HKB cos ( 2p₀ ) . H        0 H H       H     B      H B        0

Очевидно, что при K_H = K B пространственное распределение амплитуды 1-й ВРЧ повторяет аналогичное поведение одной из ее компонент, например D_H ( r_H , z ) ,

P J ^r H , ^z ) ~ ² P o2 ^K h d h ^{( r} H , ^z ) ^{cos (e} o ) ,                                                 (26)

а абсолютное ее значение напрямую зависит от начальных фазовых соотношений в спектре накачки, т.е. от величины фазового инварианта в ₀.

• 4.    ЧИСЛЕННЫЙ АНАЛИЗ ТЕОРЕТИЧЕСКОЙ МОДЕЛИ

О справедливости отмеченных допущений (20) и (21) можно судить по пространственным распределениям амплитуд и набегов фаз отдельных компонент 1-й ВРЧ, рассчитанным по выражениям (8) и (9), рис. 3 и рис. 4. Наблюдаемые различия между P _a н ( Г н , z ) и P _a в ( Г н , z ) , ф_{п н} ( r_H, z ) и ф_{п в} ( r_H, z ) являются следствием несовпадения волновых размеров излучателя для волн накачки , участвующих в генерации этих компонент, которые, как видно, уменьшаются с увеличением Ф (кривые 1 и 2).

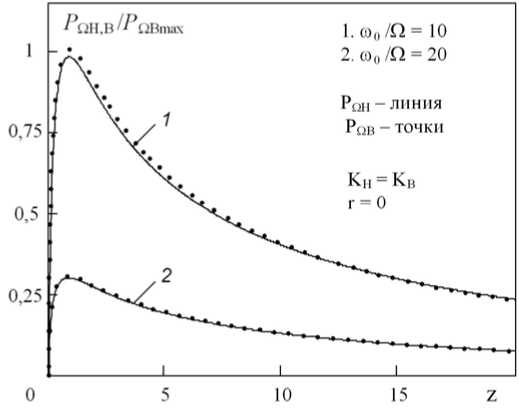
а)

Рис. 3. Осевые и поперечные распределения амплитуд компонент 1-й ВРЧ при K_H = К_в и различных значениях Ф = ю ₀ /Q

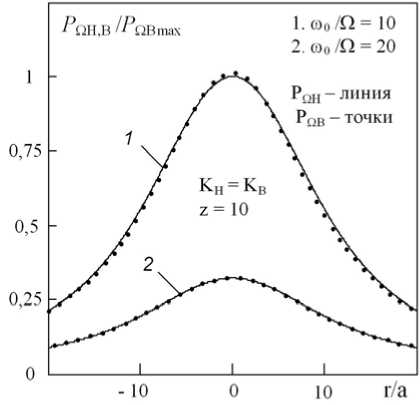
б)

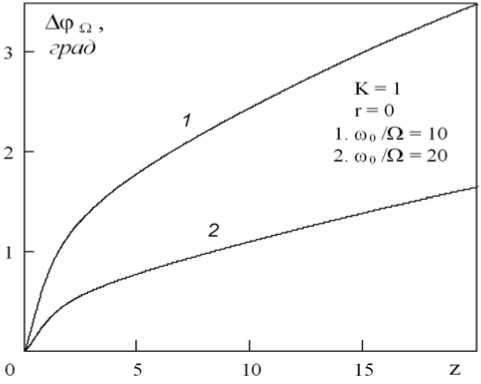
а)

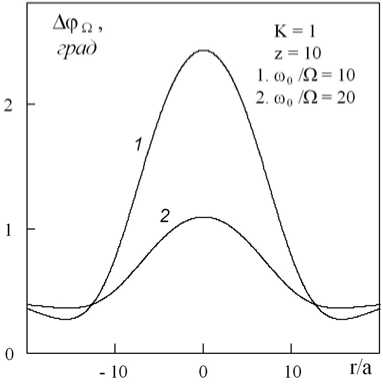
б)

Рис. 4. Осевые и поперечные распределения разности дифракционных набегов фаз у компонент 1-й ВРЧ при K = К_в /К_н и различных значениях Ф = го ₀ /Q

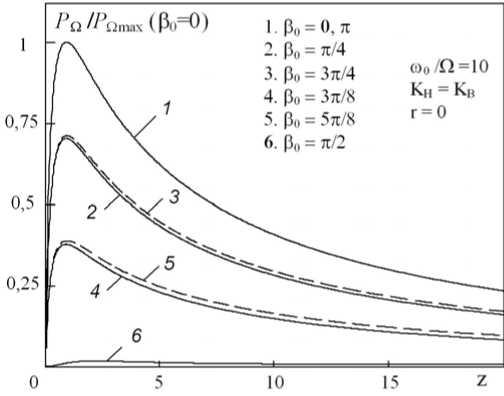
Влияние фазовых соотношений в спектре трехчастотной накачки на поле 1-й ВРЧ показано на рис. 5, где в качестве параметра выступает начальное значение фазового инварианта Р 0 . Амплитудный спектр начального возмущения симметричен ( K H = K B ) и остается неизменным для всех приведенных зависимостей. Максимальное значение амплитуда ВРЧ принимает при р ₀ = 0, п ,..., n п , когда коллинеарно и синхронно распространяющиеся волны P _n H и P _n B синфазны (с точностью до малой величины Аф_п ) и происходит их сложение. Наоборот, в случае Р ₀ = п/ 2, 3п/2,..., ( 2 n + 1 ) п/ 2 из-за противоположных фаз эти волны взаимно вычитаются, приводя практически к прекращению генерации 1-й ВРЧ.

Таким образом, при изменении фазового инварианта от нуля до п/2 происходит постепенное снижение эффективности нелинейной генерации ВРЧ от максимально возможного значения (для фиксированных параметров исходного возмущения ю ₀, Ф , P 0 и K H B ) до некоторого минимума. Данная зависимость от Р ₀ имеет периодический характер, что видно из выражения (26), и хорошо согласуется с результатами эксперимента [7].

а)

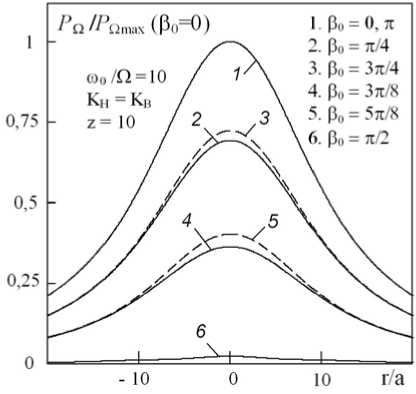
Рис. 5. Осевые и поперечные распределения амплитуды 1-й ВРЧ при K H = K B и различных значениях фазового инварианта Р ₀

б)

Неполная компенсация 1-й ВРЧ при Р ₀ = п/ 2, что видно на примере конечных значений ее амплитуды (кривые 6 на рис. 5), происходит в результате частотнозависимого характера дифракционных и диссипативных процессов. Несмотря на близость частот волн накачки, вклад этих процессов отличается для компонент P _n H и P _n B , что видно на рис. 3 и рис. 4. Наблюдаемое на рис. 5 несовпадение кривых 2 и 3, а также кривых 4 и 5, построенных при одинаковых расстройках фазового инварианта относительно Р ₀ = п/ 2, происходит из-за неравенства дифракционных набегов фаз ^ф О H ^{( r} H , z ) ^{и ф} О B ^{( r} H , z ) •

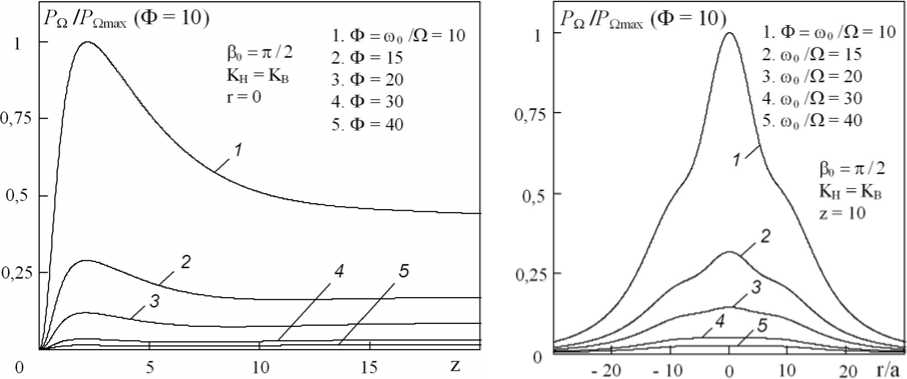
С увеличением частотного параметра Ф при условии й ₀ = const ширина спектра волны накачки сужается, приводя к уменьшению различий в пространственных распределениях первичных волн с частотами ю H , ю ₀ и ю B . Это в свою очередь приводит к более строгому выполнению равенств (20) и (21). В результате уровень остаточного поля 1-й ВРЧ в режиме фазового запрета по мере роста величины Ф достаточно быстро спадает, стремясь к нулю, рис. 6. В рамках рассматриваемой теоретической модели это соответствует переходу от выражения (19) для амплитуды ВРЧ, учитывающего неравенство полей P _{Q H} ( r_H , z ) и P _{Q B} ( r_H , z ) , к более простому соотношению (25), где эти различия становятся пренебрежимо малыми. На поперечных распределениях, рис. 6-б, прослеживается процесс “уравнивания” угловых зависимостей полей двух компонент при Ф >  20, что проявляется как в быстром уменьшении остаточной амплитуды, так и на примере постепенного исчезновения характерных ступенек на боковых скатах характеристики P _n ( r_H ) .

а)                                                     б)

Рис. 6. Осевые и поперечные распределения амплитуды 1-й ВРЧ в режиме фазового запрета ( Р ₀ = п/2) при K_H = K B и различных значениях Ф = ю ₀ /Q

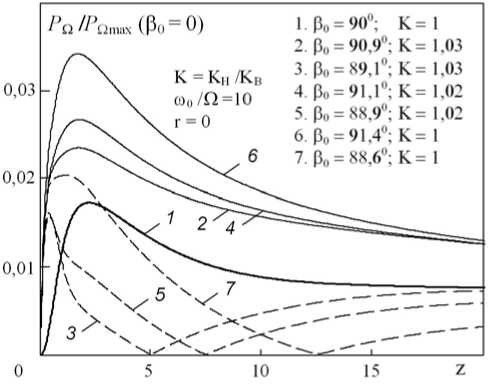
Более детально механизм “запрета” генерации 1-й ВРЧ можно проследить, создавая небольшие изменения амплитудных и фазовых соотношений в трехчастотной накачке. На рис. 7-а показано семейство осевых распределений P^(z), рассчитанных для ряда значений фазового инварианта в окрестности Р0 = п/2. Амплитудные соотношения K = KH/KB подбирались из условия получения нулевых значений амплитуды. Видно, что равные по величине приращения инварианта ДР0 =± 0,90 и ± 1,10 приводят к качественно различному поведению Pn(z), указывая на присутствие конечного значения набега фаз Дфп(r,z), величина и знак которого определяются дифракцией пучка и не зависят от в0. Отметим, что формирование и изменение местоположения локальной области с нулевой амплитудой на осевом распределении амплитуды 1-й ВРЧ посредством незначительных изменений симметрии амплитуд боковых составляющих спектра накачки (1_2%) и фазового инварианта (ДР0 < 30) наблюдалось в эксперименте [8].

а)

б)

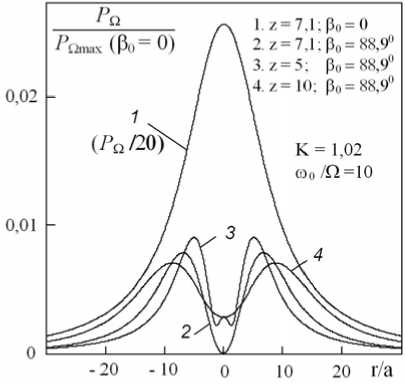
Рис. 7. Осевые и поперечные распределения амплитуды 1-й ВРЧ в режиме фазового запрета при изменении амплитудных и фазовых соотношений

в спектре накачки

Интерференционный характер формирования результирующего поля 1-й ВРЧ, представляющего собой не что иное, как суперпозицию полей P _n H и P _{n B}, виден на примере поперечных распределений амплитуды P _n ( r H ) , рассчитанных для трех расстояний от излучателя ( z = 5; 7,1; 10), рис. 7-б. Локальный максимум на кривой 3 в приосевой области пучка на малых расстояниях от излучателя ( z <  7,1) демонстрирует доминирование компоненты P _{n B} над P _n H . При r H >  2 ситуация обратная, т. е. P nH >  P nB • На расстоянии z = 7,1 и r H = 0 амплитуды компонент оказываются равными, в результате чего происходит их полное взаимное вычитание и образование нулевой точки, кривая 2. На расстояниях z >  7,1 неравенство P _n H >  P _{n B} имеет место при любых r_H , кривая 4. Для сравнения абсолютных значений амплитуды 1-й ВРЧ при разных режимах работы НАИ кривой 1 показано распределение P _n ( r H ) при Р ₀ = 0 с учетом множителя 1 20 . Экспериментальные зависимости, аналогичные распределениям на рис. 7-б, были получены в работе [8].

• 5.    АМПЛИТУДНО-ФАЗОВЫЕ ХАРАКТЕРИСТИКИ ПЕРВОЙ ГАРМОНИКИ ВРЧ

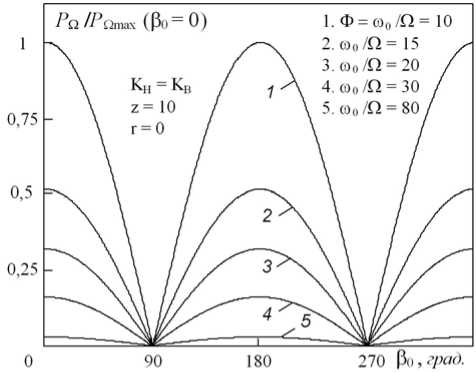
Амплитудно-фазовые характеристики (АФХ) 1-й ВРЧ представляют собой зависимость ее амплитуды от величины фазового инварианта трехчастотной волны накачки Р0. АФХ, рассчитанные согласно (19) для разных значений частотного параметра Ф = ю0 /О при условии симметрии начального амплитудного спектра накачки (KH = KB ), показаны на рис. 8-а. Зависимости Pn(p0) имеют явно выраженный периодический характер с минимумами при Р0 = п/2, 3п/2,... и максимумами при Р0 = 0, п,... Несложно убедиться, что при изменении в широких пределах разностной частоты О (или параметра Ф) АФХ достаточно хорошо описывается упрощенным выражением (26). Это согласуется со случаем взаимодействия одномерных волн и результатами эксперимента [9].

а)

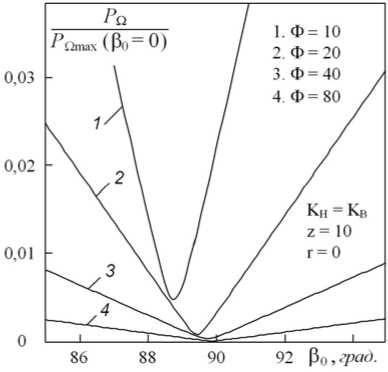
Рис. 8. Амплитудно-фазовые характеристики 1-й ВРЧ при K H = K B , z = 10, r = 0 и различных Ф = ю ₀ /О

б)

Влияние дифракции проявляется главным образом в области минимумов АФХ, что отражено на рис. 8-б. Видно, что дополнительные набеги фаз, вызванные дифракцией пучка, приводят к смещению минимума в сторону меньших, чем Р ₀ = п/ 2, значений фазового инварианта. Величина этого смещения возрастает по мере увеличения частоты О , отражая усиливающиеся различия дифракционных процессов (набегов фаз) у волн накачки с частотами ю H , ю ₀ и ю B . В подтверждение данного вывода обратим внимание на тот факт, что ближе всех к в ₀ = п/ 2 находится минимум у АФХ 1-й ВРЧ, генерируемой наиболее узкополосной накачкой ( Ф = 80). Помимо смещения АФХ вдоль горизонтальной оси при уменьшении Ф = ю ₀ /О растет и амплитуда волны в области минимума. Это является следствием усиления различий пространственных распределений амплитуд компонент 1-й ВРЧ P _n H ( r_H , z ) и P _{n B} ( r_H , z ) , которые в свою очередь обусловлены ростом отличий между полями первичных волн [8]. Аналогичные смещения минимумов АФХ при изменении разностной частоты явно прослеживаются в эксперименте [10].

Поскольку режим фазового запрета предполагает одновременно баланс амплитуд и баланс фаз (19) в рассматриваемой точке пространства, т. е.

P H ^{( r} H , z ) ’ d h ^{( r} H , z ) = P B ^{( r} H , z ) ’ d b ^{( r} H , z ) ;

Ж +Лфп( rH, z ) = n, то невыполнение одного из этих условий будет приводить к конечному значению амплитуды 1-й ВРЧ в области минимума ее АФХ. Так, например, при выполнении условия (28) неравенство между амплитудами компонент PnH и PnB приводит к тому, что АФХ принимает вид, показанный на рис. 9. При этом местоположение максимумов и минимумов характеристик практически не меняют своего положения относительно оси Р0. Сплошными линиями и точками показаны АФХ, относящиеся к случаям, когда амплитуды боковых составляющих в спектре накачки, оставаясь неравными друг другу (KH ^ KB), поочередно доминируют друг над другом, сохраняя между собой равные соотношения. При этом различия между кривыми, показанными сплошными линиями и точками, из-за влияния дифракции весьма малы, что подтверждает результаты расчета для двух других моделей НАИ — модели Вестервельта и модели “рупорного” нелинейного излучателя [10].

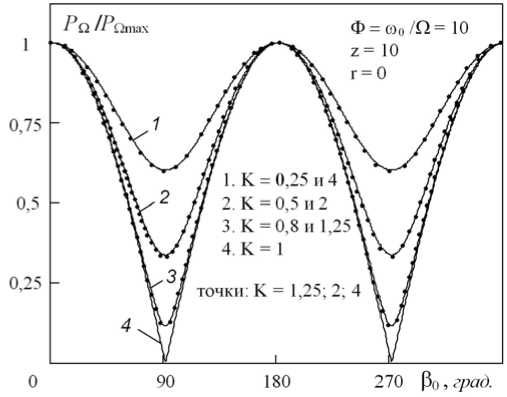
Рис. 9.

Амплитудно-фазовые характеристики 1-й ВРЧ при Ф = 10, z = 10, r = 0 и различных K = K _H / K B

ЗАКЛЮЧЕНИЕ

В рамках проведенного рассмотрения предложена теоретическая модель НАИ, учитывающая дифракцию и диссипацию первичных и вторичных волн при нелинейной генерации 1-й ВРЧ трехчастотной волной накачки с симметричным частотным спектром и произвольными амплитудно-фазовыми соотношениями, в рамках которой 1. прослежено влияние амплитудного и фазового спектров накачки на пространственные характеристики 1-й ВРЧ, качественно подтверждающее основные закономерности, присущие другим моделям НАИ;

• 2.    на примере пространственных характеристик 1-й ВРЧ и входящих в ее состав компонент показано, что дифракционные набеги фаз и изменения амплитуд волн накачки оказывают существенное влияние на реализацию режима фазового запрета, препятствуя полному подавлению ВРЧ;

• 3.    исследовано влияние частотных соотношений (параметр Φ ) на пространственные распределения и АФХ, подтвердившее усиление роли дифракционных процессов на формирование поля 1-й ВРЧ по мере расширения спектра накачки;

• 4.    выявлен ряд закономерностей в поведении 1-й ВРЧ, вызванных дифракцией пучка, которые согласуются с результатами эксперимента.