Теоретические исследования процесса удаления жидкости из зеленой массы кукурузы при силосовании

Введение. Животноводство – важнейшая отрасль сельскохозяйственного производства. Эффективность его развития во многом зависит от наличия в хозяйствах прочной кормовой базы. Поэтому повышение качества заготовляемых кормов, снижение их стоимости и потерь – первоочередная задача в кормопроизводстве, которая может быть решена не только внедрением передовых технологий заготовки объемистых кормов, но и соблюдением требований технологий. Одним из важнейших видов объемистых кормов, используемых в рационах сельскохозяйственных животных, является силос. Кукурузный силос является молокогонным кормом из-за значительной влажности, поэтому преимущественно используется для кормления крупного рогатого скота. Главная задача силосования – максимально сохранить питательность исходной зеленой массы. Важными моментами в приготовлении силоса являются определение периода максимальной энергетической и питательной ценности растения, степень измельчения, которая имеет прямую зависимость от исходной влажности, уплотнение, герметизация, соблюдение агротехнологических сроков. Заготовку кукурузного силоса ведут, как правило, в осенний период, когда возможны дождевые осадки. Влажность кукурузной массы является очень важным фактором, который обуславливает не только сроки хранения силоса, но и соотношение питательных веществ в силосной массе. На силос заготавливают кукурузу с початками в конце молочно-восковой и в начале восковой её спелости. Влажность кукурузы в этой фазе спелости зерна составляет 60–70%, что оптимально для силосования. Из измельченной зеленой массы кукурузы такой влажности при силосовании не вытекает жидкость, что создает лучшие условия для консервирования кислотой за счет интенсивного размножения молочнокислых бактерий. Влага в зеленой массе кукурузы может быть: связанной механически, химической или свободной. Свободная влага, попавшая в массу в виде осадков в дождливую погоду, может быть достаточно легко удалена. Физико-химически связанная влага появляется в результате резких перепадов температуры. Химически связанная влага находится внутри зерен, и стебель кукурузы, являясь их частью, и влияет на их свойства. Удаление этого типа влаги меняет технологические особенности кукурузы и нарушает структуру белков, жиров и углеводов данного продукта [1, 2]. Стратегия уборки кукурузы должна заключаться в том, чтобы не допустить больших потерь питательных веществ при закладке силоса. Соблюдение агротехнологических сроков уборки кормовых культур, закладки и герметизации силосуемой массы – основное условие получения готового корма высокого качества с минимальными потерями питательных веществ. На качество силоса пагубно воздействует высокая влажность заготавливаемой массы, так как усиливается интенсивность развития маслянокислых, а также гнилостных бактерий, что ведет к порче заготавливаемого силоса. Попадание воды в силосную массу приводит к потерям питательных веществ и повышению кислотности, что значительно снижает питательную ценность силоса, уменьшает его поедаемость. В итоге использование в рационе низкокачественного силоса способствует снижению продуктивности животных и качества производимой продукции, к нарушению здоровья. При силосовании избыточно влажной массы (80–86%) наблюдается большое количество сока (15–25% от её количества), что обуславливает бурное развитие нежелательных микроорганизмов, которые разлагают до 20% наиболее ценных питательных веществ [3–6]. Современные технологии приготовления и хранения силоса не исключают попадание в силос дождевой воды при заготовке зеленой массы и при закладке её в хранилища. Особенно в дождливое время в сезон заготовки силоса. Даже если в процессе заготовки зеленой массы рабочими органами уборочных машин будет удалено некоторое количество воды со стеблей и листьев кукурузы, то немалая часть её останется в измельченной массе. Осушение кукурузы от дождевой воды в естественных условиях зависит от погоды и может занять длительное время. Поэтому для того, чтобы проводить заготовку силоса вне зависимости от погодных условий, при этом получать качественные корма в дождливую погоду, следует осушать измельченную массу от дождевой воды до момента закладки ее в хранилище [7– 9]. Разработан способ (патент РФ 2683521), позволяющий вести заготовку силоса в дождливую погоду. Для этого используется вакуумированный контейнер с отводом жидкой фракции для приготовления и хранения силоса [10, 11]. Способ приготовления и хранения силосованного корма включает заготовку зеленой массы растений с их измельчением, загрузку в контейнеры, осушение, герметизацию и вакуумирование с последующей доставкой к местам хранения и скармливания. Осушение силосной массы осуществляют до герметизации и последующего вакуумирования путем просасывания через нее воздуха с попутным отводом сока и дождевой воды. Для создания воздушного потока используют вакуумный насос, а для сбора жидкой фракции – вакуумный баллон. В качестве источника вакуума лучше использовать агрегат доильный типа АИД-1, а в качестве контейнеров

– Биг-беги с полиэтиленовыми вкладышами. При этом удаляется свободная влага перед герметизацией контейнера, что исключает интенсивность развития гнилостных бактерий с получением качественного силоса. Для выявления режимов процесса при заготовке силоса в контейнерах направлены теоретические исследования, приведенные ниже.

Материалы и методы исследования. Измельченная масса кукурузы является пористой средой. В этой среде находится свободная вода, которую необходимо удалить. Для осушения измельченной массы, упакованной в мягкий (полимерный) контейнер, снизу производится откачка воздуха из него [11]. В результате этого образуется вертикальный поток воздуха сверху вниз через измельченную массу. Воздушный поток увлекает за собой частицы жидкости и удаляет её из мягкого контейнера.

При решении вопросов фильтрации методами гидродинамического анализа приходится пользоваться упрощенными моделями строения пористой среды. Одной из таких моделей является «идеальная пористая среда», у которой капиллярные каналы, составленные из пор, образующихся частицами среды, принимаются цилиндрическими и параллельными между собой (рисунок 1) [12].

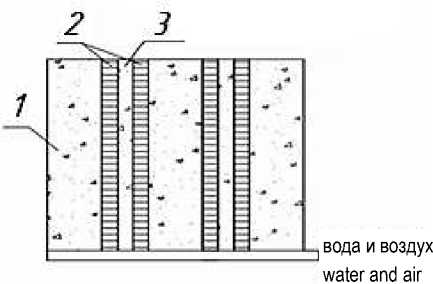
Вода в ненасыщенном состоянии обволакивает частицы измельченной кукурузы, образуя просвет, в котором находится воздух. Будем считать, что просветы образуют вертикальные трубки, по которым движется воздух. Диаметры этих трубок малы, поэтому движение воздуха по трубкам будем считать одномерным со средней скоростью v x . Кроме этого, движение воздуха в

(dv . idv²\ .dp . _f 2 ^p \^ ⁺ ~2-^ )⁺^ ^{+ f}T7₀^- P3-°,

где fT - сила трения по боковой поверхности      r0=dо/2 - радиус трубки, зависящий от коли- столба воздуха о воду, приходящаяся на еди- чества воды в измельченной массе.

ницу площади боковой поверхности;

трубке будем считать ламинарным, адиабатическим и изотермическим, а сам воздух баротропным.

Рассмотрим бесконечно малый столб воды и воздуха высотой dx в одной трубке (рисунок 2).

Используя метод кинетостатики, придем к уравнению движения воздуха

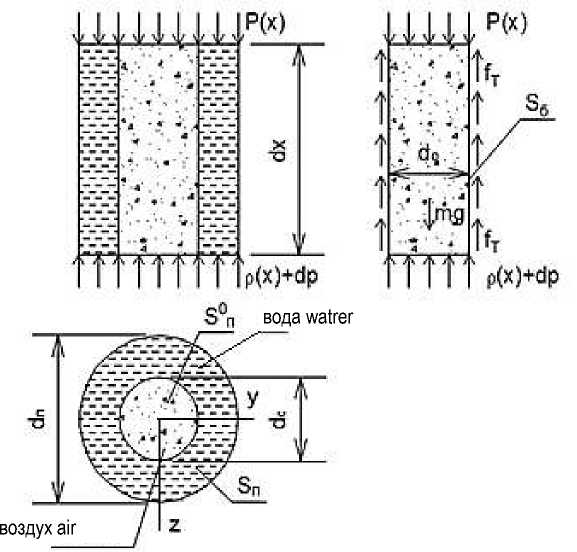
dп – диаметр поры; dо – диаметр столба воздуха; Sп – площадь поперечного сечения поры; S0п – площадь просвета; Sб – площадь боковой поверхности столба воздуха Рисунок 2 – Бесконечно малый элемент столба воздуха и воды dп – pore diameter; dо – air column diameter; Sп – pore cross-sectional area;

S⁰ п – gap area; S б – sidel surface area of the air column

Figure 2 – Infinitely small element of an air column and water

Уравнение состояния для воздуха примем в виде [12, 13]

P (p) = PoQ^r ,          (2)

где P 0 и ρ 0 – давление и плотность воздуха в естественном состоянии вверху контейнера; показатель степени γ для воздуха заключается в пределах

1 1,4.

Процесс движения будем считать установившимся, тогда уравнение (1) примет вид dV _ dP          r 2

^pV^ = -^ ^{+ P5-}^ ; ?     ⁽³⁾

(

Р о У о² Р о^1/У Р ^-(^⁺¹⁾ У

где V₀ = (—)   V_B - скорость воздуха в нача-

^P 0

ле трубки.

Воду будем считать несжимаемой, а её движение установившимся. Это означает, что скорость течения воды одинакова во всех точках по высоте трубки (зависит только от радиальной координаты). Следовательно, сила трения f_T должна быть постоянной по высоте трубки вдоль линии тока.

а уравнение неразрывности принимает вид

Т = ⁰ '            (4)

где р, V , Р - зависят только от х .

К уравнениям (3), (4) необходимо добавить граничные условия:

при х=0 Р=Р о , р=р о , при x=h Р=Р в , V = V_B.    (5)

где Р в , V_B - давление и скорость воздуха внизу контейнера.

Выражая скорость через давление из уравнения состояния (2) и неразрывности (4), придем к уравнению

+ i)^ = P o P o~ ^1/rP^g

² f rn Г о .

Считая f_T постоянной и пренебрегая силой тяжести воздуха, в результате интегрирования уравнения (6) по высоте трубки, получим выражение для силы трения:

f, = ^r-^,                    (7)

где ^V-^fer-l)-

Сила трения fт по отношению к воде является поверхностной нагрузкой, распределен- ной по внутренней поверхности цилиндра, и направлена вниз. Поскольку рассматриваем

ординат, в которой с учётом (4) оператор Лапласа имеет вид

одномерное установившееся движение воды и воду считаем несжимаемой, то уравнение На-вье–Стокса [13] принимает вид

^--pg = vAV,            (8)

где V - коэффициент вязкого трения между

а уравнение (8) –

AV = ^V + 1— , dr ² г dr

дР дх

-

pg = v(^+~B (io)

слоями жидкости.

В пределах одной трубки движение воды является осесимметричным. Поэтому удобно воспользоваться цилиндрической системой ко-

Решение уравнения (10) при граничных условиях V(x,r_K) = 0 , д^ = -2^ при r=r o и равенстве (7) является следующим:

^V(r) = [ 1 ^{F (} r k ^{— r} 2 ) ^{+ (1f —} Q ^)r o2 ^ln3 ]¹ .

В гидродинамике подземных вод вводят среднюю скорость по активному сечению трубки [12]:

V o =^£ ^K V(r)rdr.                         (12)

^г к ^Г 0    ' 0

Подставим в (12) выражение скорости (11) и проинтегрируем. В результате придем к выражению

Vo = — —^{(Гк — r²)² — 8( 1 ⁰     8v(r£-r 2 ) I к                ^V2

Из (11) следует, что при r 0 =0 (полностью заполненная трубка) выражение скорости V(r) совпадает с формулой Стокса, а формула (13) – с формулой Гагена-Пуазейля в гидравлике.

Расход воды через все активные поровые трубки равен:

Q = NSn ⁽ r 2 ^{— r} o ^{2 )V} o .

l^)r2 ^(r 0 ^{2 ln} ( г ; ) ^{+ 1 (r} K ^{2 — r 2 ))}} -          ⁽¹³⁾

Или с учетом (13)

Q =^ r ^K f_u (^{r o} ) ,        (14)

где N – число пор, приходящихся на единицу площади поперечного сечения контейнера;

S – площадь поперечного сечения контейнера.

" ( Г 0 ) = (1 — ( г к )²)²—8( 2 —£ ( г к )² fe)² О+Id — ( г к )²)) ■      (15)

Коэффициент активной пористости с учётом того, что не вся вода в порах приходит в движение, равен:

П= ^ р ,             (16)

где V пр – объем просветности кукурузного сырья в контейнере;

V = Sh - объем корма в контейнере. Объем просветности силоса в контейнере

Vnp = N^rK2Sh.(17)

Подставляя равенство (17) в (16), получим для активной пористости выражение п = Nm\2.(18)

С учётом (18) формула (14) для расхода воды из силоса в контейнере принимает вид

Q  —-У(^|.

В насыщенной пористой среде все поры полностью заполнены жидкостью, поэтому в них r 0 = 0. Как следует из (15),  U(0) =  1, т.к.

lim r 0 ^o r o ⁴ ln r o = 0 .

С другой стороны, расход жидкости в насыщенной среде по закону Дарси [12, 14]:

Q = pg ^k           (20)

где k - коэффициент фильтрации насыщенной среды.

Сравнивая выражения (19) и (20), прихо- дим к равенству п-Гк _ к v     pg ■

Подставив (21) в (19), получаем формулу для расхода жидкости через поперечное сечение контейнера:

Q=p>@-       (²²⁾

В выражении (22) величину k U

мож-

Установим зависимость

функции U

но рассматривать как переменный коэффици-

®

от объема воды в измельченной массе. Для

ент фильтрации, зависящий от влажности из-

мельченной массы.

этого выразим объем воды через размеры активной поровой трубки:

К (0 = m(r 2

—

r 02 (t))hNS или V_B(t) = mr^N

—

Воспользовавшись равенством (18), придем к выражению

V , (t) = nV(1 —^) .    (24)

Из (24) находим

5=1—-^—“W'    (25)

vB(t)

где u(t) = - содержание воды по отношению к объему активных пор; V_n = nV - объем пор в силосе. Подставив (25) в (15), получим зависимость U (^) от объёма воды в силосе.

U ( 0 ) = u(t)² — 8Е(1 — u(t)) ((1 — u(t))l n^1 — u(t) + - u(t) ² ).         (26)

Объём откаченной воды из контейнера за время t

V^t) = £ Q(t) dt = ^£ U(u(t))dt.

Чтобы вычислить интеграл в (27), необходимо иметь аналитическую зависимость текущего объёма воды в силосе от времени откачивания, которую можно получить на основе опытных данных. Процесс откачивания воды можно представить в виде графика, показанного на рисунке 3.

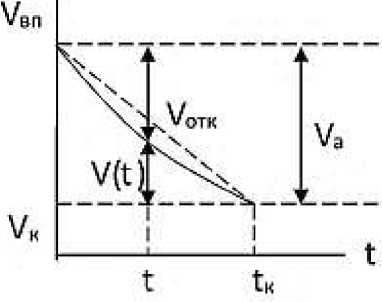
V вп – объём воды до откачивания; V к – объём воды, оставшейся в корме;

V(t) – текущий объём воды сверх оставшегося; V отк (t) – откаченный объём воды в момент времени t;

V a – активный объем воды – объем воды, поддающийся откачиванию

Рисунок 3 – Зависимость текущего объёма воды в силосе от времени откачивания

V вп – volume of water before pumping; V s – volume of water remaining in the stern;

V(t) – current volume of water in excess of the remaining; V pum (t) – pumped volume of water at a time t;

V a – active water volume – volume of water accessible to pumping

Figure 3 – Characteristic volumes of water removed from the crushed mass depending on the pumping time

Кривую зависимость V(t) можно аппроксимировать различными функциями, например линейной функцией (в нулевом приближении), по времени (рисунок 1 – штриховая линия).

V(t) = Va(1—^-)=u(t)V„

где V a = V en — V k .

Рассмотрим случай линейной аппроксимации (28). Перейдём от интегрирования по t к интегрированию по u(t). Выразим t через u(t) :

u(t) ^t= ( ^1-— )^ ‘ - тогда дифференциал dt = -^du(f) .

Из (28) находим u(0) = ^ = G , тогда

• £ U(t)dt = -±Г^ u(u)du. (29) 0                G ^G

^^ U(u)du = - (u³ — G³) — E {4 [ 1 (u² — G²) — (1 — G³) (in V1 — G — -)]}.

Итак, нами получена теоретическая зависимость, позволяющая определить объём удаляемой свободной жидкости из зеленой массы кукурузы при её силосовании в контейнере в зависимости от времени откачивания воздушножидкостной фазы.

Результаты исследования и их обсуждение. Решать математические зависимости проще численным методом. Однако требуются экспериментальные данные. Ниже приводится решения в виде графических зависимостей с использованием опытных данных при

Выражение (27) для откаченного объёма за время t принимает вид

WO = — t ^ ^tF Jg® U(u)du .   (30)

^G P9 ^G

Интеграл в (30) от функции U(u) в виде (26) имеет следующее выражение:

• — “ (u3 — G3)] — 3 [(1 — u)3 (ln V1 — u — “) —

численных параметрах: объемный вес воды γv=10 кн/м³, атмосферное давление Р 0 =101,385 кПа, плотность воздуха ρ 0 =1,225 кг/м³, коэффициент пористости n=0,7, коэффициент фильтрации k=0,006 м/с, объем воды в силосуемой массе V вп =19·10^-3 м³, при этом от-качалось воды V к =4,3·10^-3 м³, время откачивания t к =10 мин, скорость воздуха на выходе v к =22 м/с [15].

При фиксированных значениях решение в комплексе Mathcad и полученных выражений (30), (31) будет представлено рисунком 4.

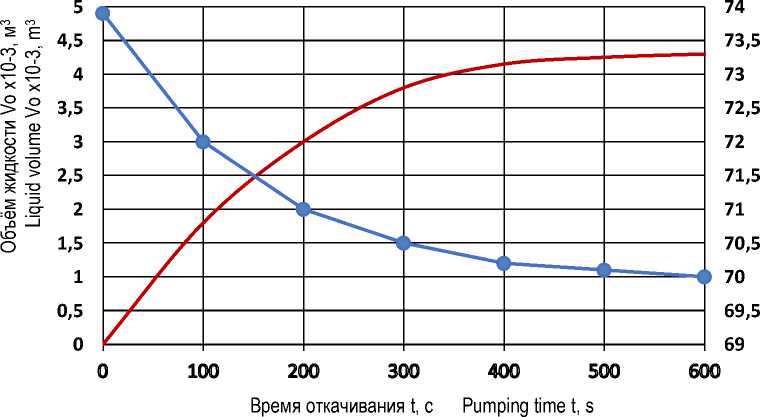
Объём жидкости             Влажность зелёной массы

Liquid volume                  Humidity of green mass

Рисунок 4 – Графические зависимости объема удаленной жидкости из зеленой массы V o , её влажности W от времени откачивания t

Figure 4 – Graphical dependences of the volume of liquid removed from green mass V o , its humidity W on pumping time t

Следует отметить, что полученная зависимость (рисунок 4) является неудобной при практическом применении. В процессе заготовки силоса наиболее удобным параметром является влажность зеленой массы. Поэтому на рисунке 5 представлена зависимость изменения влажности зеленой массы за счет удаления воды из неё при силосовании в контейнере от времени откачивания.

Анализ зависимости показал, что снизить влажность зеленой массы с 73,9 до 70,0% можно за 600 секунд в рассматриваемых условиях, а объем откачанной жидкости при этом составит 4,3·10-3 м3. Осушением кукурузной массы от дождевой воды при заготовке силоса в контейнере можно значительно сократить время по сравнению с естественными условиями, которые зависят от погоды.

Выводы. Чтобы обеспечивать получение качественного силоса вне зависимости от погодных условий, следует осушать измельченную массу от дождевой воды до момента закладки ее в хранилище. Осушение кукурузы от дождевой воды в естественных условиях зависит от погоды и может занять длительное время. Разработан способ приготовления и хранения силоса, позволяющий вести заготовку зеленой массы в дождливую погоду с использованием вакуумированного контейнера с отводом жидкой фракции из него при закладке до герметизации.

В результате выполненных теоретических исследований процесса предварительного удаления свободной жидкости из измельченной массы кукурузы при силосовании в контейнере получено выражение для определения объема выведенной воды в зависимости от времени процесса. Полученные результаты позволят рассчитывать технологические параметры процесса закладки кукурузы на силос и разработать средства механизации для удаления излишней влаги из силосуемой массы. В конечном результате это позволит значительно повысить качество заготавливаемого силоса и сократить его потери при хранении.