Теоретические основы оболочки для интерактивных систем верификации интуитивных математических доказательств

В математической литературе доказательства теорем в теории доказательств получили название интуитивных. Проверка правильности (верификация) интуитивных доказательств теорем является одной из важнейших задач в математических исследованиях [1]. Правильным доказательством может считаться только полное доказательство, выполненное в рамках формальной системы, для которой справедливо утверждение о том, что если для математического утверждения может быть построено доказательство (вывод), то оно истинно (логически общезначимо) [2]. Однако в математической практике, связанной с построением доказательств теорем вручную, такие доказательства не строятся в силу их громоздкости, а также чрезмерной трудоёмкости этого процесса. Отмечается [3,4], что в математической литературе существует давняя традиция ошибок. Ошибки в доказательствах могут оставаться незамеченными на протяжении долгого времени, а их исправления не публикуются настолько часто, как следовало бы.

В 1994 г. был опубликован QED-манифест [5] анонимных авторов, в котором выдвинуты амбициозные цели - построение корпуса механически (автоматически) верифицированной математики, в том числе формализации математических доказательств, и проверки их правильности.

На сегодняшний день перспективным направлением использования компьютеров для решения задачи обеспечения правильности интуитивных доказательств является разработка интерактивных систем поддержки построения доказательств (СППД) теорем. Они оказывают помощь при вводе формализованного полного доказательства и обеспечивают его правильность (MINLOG, KeY Proover, JProver, ACL2, Mizar, Lean, Matita, ProofPeer, Agda, Nuprl, Epigram и др.) [6-8]. В качестве формальной системы в таких СППД обычно используется либо язык логики предикатов первого порядка, либо язык, основанный на некотором варианте логики предикатов высших порядков или теории типов (строго типизированном Х -исчислении) с развитым, общепринятым синтаксисом арифметических, теоретико-множественных и, возможно, иных выражений [6,7].

Следствием многообразия специализированных логик, с одной стороны, и большой трудоёмкости создания программного средства, реализующего построение доказательств в рамках каждой такой логики или адаптации существующего средства к другой логике, с другой стороны, явилась разработка логико-независимых программных оболочек для создания СППД (PVS, Twelf, Coq, HOL Light, Isabelle/HOL, LCF, БУЦЕФАЛ и др.) [1,6,7,9]. В таких оболочках предлагаются метаязыки для формализации математических знаний и дедуктивных систем (исчислений). В качестве таких метаязыков обычно используются языки программирования, основанные на функционально-императивной парадигме, либо на некотором варианте строго типизированного Х -исчисления с развитой параметрически полиморфной системой зависимых типов и параметризуемыми модулями. При этом для описания правил математического рассуждения используется процедурный подход.

Достоинством разработанных СППД является то, что для используемых в них формальных систем справедливо утверждение о том, что истинность математического утверждения следует из возможности построения его доказательства. Многие из современных СППД успешно применялись для верификации доказательств сложных математических теорем [1].

Однако существующие СППД до сих пор оказываются невостребованными большинством математиков в их исследованиях. Это подтвердил опубликованный в 2007 г. пересмотренный манифест [10], в котором хотя и подтверждались цели исходного манифеста, но констатировалось, что за время, прошедшее с момента его опубликования, не было сделано существенного продвижения в достижении его целей. Там же указывалась и одна из основных причин такого положения дел: формализованная математика совершенно непохожа на реальную. Исходя из этого, можно заключить, что основное препятствие к широкому использованию СППД состоит в том, что в них используются формальные логические системы, далёкие от представлений математиков, выполняющих такую работу. Формализация математических теорем и их доказательств остаётся для математиков сложным процессом; по-прежнему существует крутая кривая обучения, препятствующая принятию математическим сообществом такого стиля работы с доказательствами [1]. Этот процесс ориентирован на специалистов по математической логике, обладающих знаниями значительной части теории доказательств, теории типов, теории моделей, теории множеств и т.п.

В цикле работ [11-13] для верификации математических доказательств была высказана идея приближения формальной модели, лежащей в основе СППД, к математической практике. В настоящей работе описывается декларативная метамодель для представления формальных логических систем, приближенных к математической практике (связанной с конструированием интуитивных доказательств), и способы использования этой метамодели для описания таких формальных систем. Предлагаемая метамодель ориентирована на разработку и реализацию на её основе программной оболочки для систем верификации интуитивных математических доказательств.

1    Концепция оболочки

Как известно, математический диалект и способы математических рассуждений не только не являются фиксированными, явно описанными, но и продолжают развиваться по мере развития математики. Поэтому нет никакой возможности построить такую фиксированную формальную систему, которую можно было бы положить в основу СППД, и “проекция” с языка математического диалекта на которую не была бы чрезвычайно громоздкой и сложно осуществимой для большинства математиков. Тем не менее, во всех известных авторам СППД используются языки с фиксированным синтаксисом для представления математических утверждений и их доказательств, а также фиксированные множества правил рассуждений, что означает невозможность их изменения без внесения соответствующих изменений в код программной системы.

Чтобы иметь возможность приближать формальные логические системы к математической практике, они должны быть расширяемыми. При этом возможность их расширять должны иметь не только разработчики СППД, но прежде всего пользователи таких систем - члены математического сообщества.

Одним из способов обеспечения такой возможности является разработка для них программной оболочки (инструментальной метасистемы), которая позволяла бы создавать прикладные СППД, в основу которых уже положено ядро формальной системы, приближенной к математической практике, и предоставляла бы механизмы расширения этой системы.

Расширяемыми и изменяемыми должны быть следующие компоненты формальных систем: язык представления математических знаний , на котором описываются аксиомы, теоремы, леммы, определения и т.п., и множество формализованных способов рассуждений , доступных математику при построении доказательств теорем. Для этого способы рассуждения должны быть представлены явно, а язык представления формализованных способов рассуждений также должен быть расширяемым.

Отметим, что данные языки эквивалентны логическому языку высших порядков и не поддерживают графические образы, геометрические построения и интерпретации различных конструкций: коммутативные диаграммы, диаграммы Эйлера-Венна и т.п.

Для обеспечения расширяемости формальных систем при их разработке используется подход, основанный на контекстно-зависимых грамматиках и онтологиях. Расширяемость достигается за счёт того, что контекстно-зависимые грамматики абстрактного синтаксиса языков представления математических знаний и формализованных способов рассуждений имеют в СППД явное декларативное представление, специфицированное в соответствии с метамоделью. Благодаря этому, во-первых, способы рассуждения имеют в СППД явное декларативное представление, и, следовательно, пользователи могут изменять их множество, а также сами способы рассуждений; во-вторых, пользователи имеют возможность включать в грамматику языка представления математических знаний новые правила либо модифицировать существующие. Это же относится и к контекстным условиям.

Заметим, что при открытости для математиков баз способов рассуждений и, соответственно, расширяемости исчисления остаётся открытым вопрос, касающийся теоремы о следствии истинности математического утверждения из его доказуемости. Очевидно, что для такой формальной логической системы справедливость данной теоремы не гарантируется (более того, она оказывается неприменимой к этой формальной системе). Однако эта проблема может быть адресована специалистам по математической логике, задачей которых является исследование и верификация предлагаемых математиками способов рассуждений на метаязыке. В результате анализа среди метаматематических утверждений может быть выделен класс аксиом, а остальные классифицированы либо как требующие доказательства, либо как неверные. Тем самым, доказательства, в которых используются неверные или недоказанные метаматематические утверждения, не могут считаться верными. Общезначимость пропозициональных формул может быть проверена автоматически.

Статья посвящена описанию средств определения формальных логических систем, приближенных к математической практике, - декларативной метамодели, а также использованию этой метамодели ядра и механизмов расширения формальной системы, которая может быть положена в основу прикладных СППД, создаваемых с использованием оболочки.

Как и всякая формально-логическая модель, описываемая формальная система должна определять формальный язык для представления математических знаний - аксиом, определений, теорем, лемм и других математических утверждений; и исчисление, в котором должны строиться правильные полные доказательства, согласованное с этим языком. Определение исчисления включает в себя определение методов доказательства математических утверждений; способов рассуждений, доступных математику в процессе конструирования доказательств теорем, и формального языка для их представления; модели онтологии доказательств - структуры для представления полных доказательств. Определение формального языка включает определение его онтологии - абстрактного синтаксиса и контекстных условий, а также, возможно, конкретного синтаксиса. Абстрактный синтаксис языка может быть задан порождающей графовой грамматикой; контекстные условия - на специальном языке формул над элементами этой графовой грамматики. Поскольку в математике формулировки различных утверждений и способов рассуждений традиционно записываются в текстовом виде, то конкретным синтаксисом формальных языков в данном случае является текстовый синтаксис. Средством задания текстового синтаксиса языка является порождающая текстовая грамматика, дополняющая соответствующую графовую грамматику необходимыми элементами конкретного синтаксиса. Важно отметить, что на сегодняшний день за рамками работы остаётся практика рассуждений, принятая в современной математике, которая основана на принципе структурализма, а также понятиях изоморфизма, эквивалентности (идентичности) математических объектов [14].

2    Средства определения формальных систем

Декларативная метамодель для спецификации формальных систем состоит из языка описания порождающих графовых грамматик, языка описания контекстных условий и языка описания порождающих текстовых грамматик.

• 2.1    Язык описания порождающих графовых грамматик

• 2.2    Язык описания контекстных условий

• 2.3    Язык описания порождающих текстовых грамматик

В работах [15,16] описана орграфовая связная двухуровневая модель информационных единиц. В соответствии с этой моделью различаются два типа орграфов по уровню абстракции представляемой ими информации: орграфы, представляющие метаинформацию, и орграфы, представляющие информацию. Для этой модели предложены языки (нотация)

представления орграфов метаинформации и информации . Также определены соответствия между этими орграфами и моделью порождения орграфов информации по орграфам метаинформации, сохраняющего это соответствие. Назначение орграфа метаинформации состоит в спецификации абстрактного синтаксиса языка, в терминах которого формируется множество орграфов информации.

Таким образом, орграфы, описывающие абстрактный синтаксис языков представления различных видов знаний и данных, могут рассматриваться как порождающие графовые грамматики . Грамматика порождает множество размеченных корневых иерархических бинарных орграфов с возможными петлями и циклами (орграфов информации). Сама грамматика имеет аналогичную форму представления - в виде орграфа, обладающего такими же свойствами (орграфовое представление грамматики далее названо орграфом грамматики ) [17]. Отличие состоит в разметке: орграф грамматики имеет дополнительную разметку вершин и дуг, задающую семантику правил порождения.

Контекстные условия, проверяемые на орграфах информации, описываются на языке логико-математических формул, которые задаются над той графовой грамматикой, по которой эти орграфы информации порождаются. Контекстное условие имеет название и представляет собой кванторную формулу. Каждая переменная, входящая в формулу, связана некоторым квантором, имеет имя, а область её возможных значений задаётся термом, значением которого является множество вершин орграфа информации.

Выделяются следующие типы формул: равенство и неравенство термов; арифметические отношения над числовыми термами; теоретико-множественные отношения над термами; формулы с пропозициональными связками; кванторные формулы; предикат « прямой предок », моделирующий отношение над термами, представляющими вершины орграфа информации.

Выделяются следующие типы термов: термы, представляющие пути в орграфе метаинформации; термы, представляющие арифметические выражения; термы-кванторные конструкции; термы, представляющие операции над множествами; условный терм, моделирующий разветвлённый условный оператор; терм, представляющий конкатенацию строковых или двоичных констант; терм, значением которого является метка вершины орграфа информации; термы, представляющие константы различных типов.

Язык описания порождающих текстовых грамматик согласован с языком описания порождающих графовых грамматик и позволяет специфицировать грамматики в РБНФ1 подобной нотации, задавать некоторые виды контекстных условий, а также метасимволы форматирования текстов, используемые при их синтезе.

Текстовая грамматика представляет собой описание множества правил . Каждое правило состоит из левой и правой части . Левая часть правила представляет собой ссылку на соответствующую вершину орграфа грамматики, специфицирующего абстрактный синтаксис некоторого языка. Правая часть - последовательность элементов, каждый из которых относится к одному из следующих четырёх типов: элемент конкретного синтаксиса; элемент форматирования; ссылка на соответствующую вершину орграфа грамматики; элемент, позволяющий специфицировать контекстные условия.

Отметим, что в текстовой грамматике необходимо описывать лишь те правила, вид которых должен быть переопределён по сравнению с их видом в графовой грамматике, которой она сопоставлена. В основном это касается тех правил, в правую часть которых должны входить элементы конкретного синтаксиса, элементы форматирования и элементы, позволяющие специфицировать контекстные условия.

3    Модель онтологии базы математических знаний

С целью структурированного хранения и накопления математических знаний вводится модель онтологии для представления баз математических знаний, специфицирующая сетевую структуру различных разделов математики.

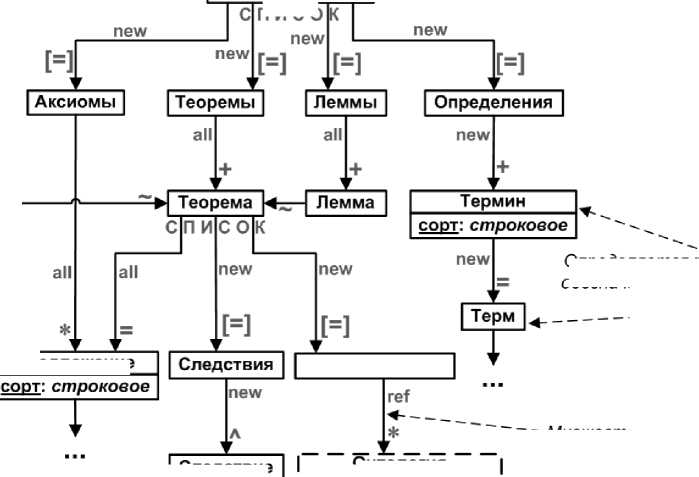
Каждый раздел математики имеет своё название и может содержать следующие множества: множество определений, позволяющих вводить новые термины для обозначения определяемых понятий, а также задавать значения этих терминов; множество аксиом; множество теорем и лемм, каждая из которых может иметь множество следствий; множество именованных подразделов (см. рисунок 1).

Онтология базы математических знаний

new

*

М

Раздел сорт: строковое

new

СПИСО

К

Математические знания ПИ С О

Следствие

- - Множество ссылок на различные доказательства теоремы -Леммы /следствия

Онтология । доказательств® । Доказательство

Рисунок 1 - Спецификация структуры разделов математики

Определяется термин, обозначающий значение терма

Предложение

| Доказательства^

Здесь и далее нотация разметки вершин и дуг, изображённых на рисунках орграфов грамматик и орграфов информации, совпадает с нотацией, используемой в [15,16], где подробно описана её семантика.

4    Язык представления математических знаний 4.1    Ядро языка представления математических утверждений

На рисунке 2 изображен фрагмент порождающей графовой грамматики, описывающей абстрактный синтаксис ядра языка представления математических утверждений. Каждое математическое утверждение (предложение) представляется вершиной графовой грамматики «Предложение » и имеет вид: ( v 1 : t 1 ) ... ( v_n: t n ) /. Здесь / - математическая формула, содержащая вхождения предметных переменных v 1 , .., v n , а ( v i : t i ) ( i = 0, .., n ) -описание предметной переменной v i , t i - математический терм, значением которого является множество (область возможных значений переменной v i ). Математическое утверждение моделирует оборот математического диалекта: «для любых значений v 1 из t 1 , .., v_n из t_n справедлива формула / ».

Выделяются следующие типы формул : равенство и неравенство термов; арифметические отношения над числовыми термами; теоретико-множественные отношения над термами; формулы с пропозициональными связками; кванторные формулы (с конечными и бесконечными областями возможных значений переменных); аппликация предиката.

Выделяются следующие типы термов : арифметические термы; различные виды интервалов, а также множеств, которые они образуют; кванторные термы (с конечными и бесконечными областями возможных значений переменных); термы-операции над множествами, а также обозначения некоторых фиксированных множеств; термы, связанные с отображениями; условный терм, моделирующий оборот математического диалекта: «если / 1 , то t i , ... если / , то t_n ».

Онтология ядра языка представления математических утверждений содержит контекстныеусловия . Они записываются на языке описания контекстных условий, но здесь приводится только их неформальное описание.

Контекстные условия на предметные переменные.

• ■   Для каждого использующего вхождения переменной в тело предложения или тело неко

торой кванторной конструкции существует определяющее вхождение этой переменной в префикс этого предложения или этой кванторной конструкции.

• ■    Для каждого определяющего вхождения переменной в префикс предложения или некоторой кванторной конструкции существует использующее вхождение этой переменной в тело этого предложения или тело этой кванторной конструкции.

• ■    Терм, представляющий собой область возможных значений определяемой переменной, не может содержать вхождений этой же самой переменной.

Контекстные условия на соответствие числа формальных и фактических параметров.

Если аппликация предиката имеет вид р ( t 1 , .„, t_m ), то:

• ■    если р есть термин , то в некотором разделе математических знаний секция « определения » должна содержать определение вида р = Л ( v 1 : tt 1 ) ... ( v_m : tt_m ) /, где / - формула, содержащая вхождения предметных переменных v 1 , .., v_m , m >  1;

• ■    если же р есть переменная , то её описание должно иметь вид р : tt 1 x „,х tt_m ^ множество логических значений , если m >  1, либо р : tt 1 ^ множество логических значений , если m = 1.

Если аппликация функции имеет вид р ( t 1 , .... t_m ), то:

• ■    если р есть термин , то в некотором разделе математических знаний секция « определения » должна содержать определение вида р = Л ( v 1 : tt 1 ) ... ( v m : tt m ) t , где t - терм, содержащий вхождения предметных переменных v 1 , .., v m , m >  1;

• ■    если же р есть переменная , то её описание должно иметь вид р : tt 1 x „.х tt m > tt , если m

• >    1, либо р: tt i ^ tt , если m = 1.

• 4.2    Механизмы расширения языка представления математических утверждений

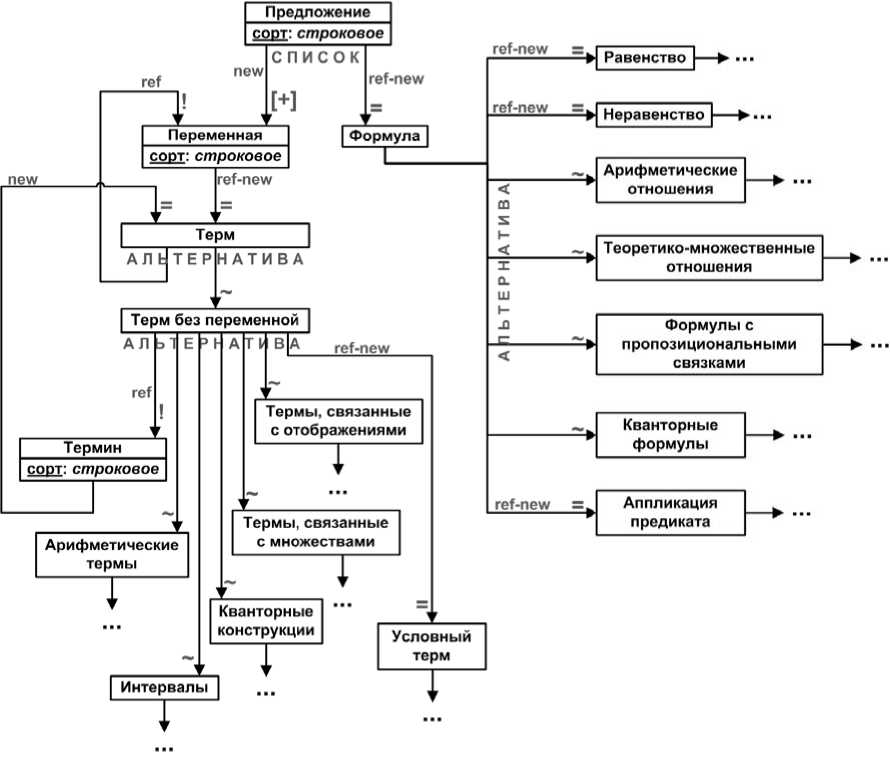
Рисунок 2 - Фрагмент орграфа грамматики, описывающей абстрактный синтаксис языка представления математических утверждений

Текстовая грамматика, описывающая конкретный синтаксис ядра языка представления математических утверждений, задаётся на языке описания порождающих текстовых грамматик и содержит 85 правил.

Расширение языка представления математических утверждений обеспечивается добавлением новых видов термов и формул. Оно состоит в добавлении новой конструкции в орграф грамматики языка, описании абстрактного синтаксиса этой новой конструкции, добавлении нужных правил в текстовую грамматику языка, а также, возможно, описании связанных с новой конструкцией контекстных условий.

5    База математических знаний

База математических знаний формируется в соответствии с моделью её онтологии. Приведём примеры определений терминов, входящих в состав математических знаний раздела «Арифметика». Данный раздел входит в ядро базы математических знаний. Определения записаны в конкретном синтаксисе языка представления математических утверждений.

• ■   множество натуральных чисел = I[ 1, да ).

• ■   множество положительных вещественных чисел = {( x: R ) x >  0}.

• ■   множество отрицательных вещественных чисел = {( x: R ) x <  0}.

Приведём примеры математических утверждений, входящих в состав математических знаний раздела «Арифметика». Это аксиомы, либо теоремы, имеющие доказательства в рамках определяемой формальной системы.

• ■    Свойство коммутативности умножения: (x : R ) (y : R ) x * y = y * x .

• ■    Правило выноса общего множителя за скобки: ( x : R ) (y : R ) ( z : R ) x * y + z * y = ( x + z ) * y .

• ■    Правило приведения к общему знаменателю дроби и числа:

( x : R ) (y : R \ {0}) ( z : R ) x Iy + z = ( x + y * z ) / y .

• ■    Теорема о сумме членов конечного отрезка натурального ряда:

( n : I [0, да )) ( Е ( i : I [0, n ]) i ) = n * ( n + 1) / 2.

Расширение базы математических знаний состоит в добавлении новых математических знаний - определений, аксиом, теорем и лемм (а также их следствий) в существующие в базе разделы математики; а также в создании новых разделов/подразделов математики и наполнении их соответствующими математическими знаниями.

6    Методы доказательств

Исчисление, в рамках которого строятся доказательства, включает методы доказательства целей , основанные на трёх правилах. Перед описанием самих правил определим понятия цель и справедливоеутверждение .

Цель представляет собой пару: математическое утверждение и, возможно пустой, список предположений - множество математических утверждений, из справедливости которых следует справедливость данного утверждения.

Под справедливым утверждением будем понимать математическую аксиому, определение, теорему/лемму (а также следствие из неё), для которой уже построено доказательство, либо способ рассуждения (см. далее - раздел 7). Определения и аксиомы считаются правильными в силу соглашения между членами математического сообщества.

Далее опишем сами правила вывода исчисления.

Правило доказательства импликации ( естественного вывода ) позволяет свести доказательство цели, математическое утверждение которой имеет форму импликации f 1 & .. &  f_k ^ f, а список предположений есть р 1 , ., p_n ( n >  0), к доказательству цели, математическое утверждение которой есть заключение этой импликации - f, а список предположений есть p i , ., p n , f i , ... , f k .

Правило сопоставления (matching) . Если ф - справедливое утверждение и существует подстановка 0 вместо переменных, входящих в ф , такая, что результат применения этой подстановки к ф совпадает с математическим утверждением f доказываемой цели или синтаксически эквивалентен / , то f справедливо (f есть конкретизация ф ). Список предположений цели в этом случае является пустым. Стоит отметить, что сопоставление представляет собой однонаправленный вариант унификации [18].

Правило отделения (Modus ponens ) , используемое для декомпозиции цели , декомпозиции некоторого предположения цели, или для вывода .

Декомпозиция цели . Если требуется доказать цель, список предположений которой есть p₁ , .., p_n , ( n >  0), а математическое утверждение f может быть сопоставлено с заключением справедливого утверждения, имеющего вид ф₁ & ... & ф_т ^ ф, и 0 - наиболее общий унификатор f и ф , то это доказательство сводится к доказательству целей, математические утверждения f i , ..., f m которых являются соответственно результатами применения подстановки 0 к утверждениям в условии этой импликации ^ = ф₁0, ..., f m = ф_т0, а список предположений каждой цели есть p₁ , ., p_n .

Декомпозиция предположения . Если требуется доказать цель, математическое утверждение которой есть f а список предположений есть p₁ , ., p i , ., p_n ( n >  1), и предположение p i может быть сопоставлено с правой частью равносильности ф справедливого утверждения, имеющего вид ф₁ \ . \ ф_т ^ ф (ф₁ v ... v ф_т ^ ф ), ( m >  2), а 0 - наиболее общий унификатор p i и ф, то это доказательство сводится к доказательству m целей, у которых математическое утверждение есть f а списки предположений суть p₁ , ., pp₁ , ., p_n , где pp₁ является результатом применения подстановки 0 к ф₁ ; ...; p₁ , ., pp m , ., p_n , где pp m является результатом применения подстановки 0 к ф_т .

Вывод , представляющий собой последовательность шагов вывода . Шаг вывода состоит в следующем. Пусть математическое утверждение fi ( i = 1, ., m ) является аксиомой, либо определением, либо доказанной теоремой/леммой (или её доказанным следствием), либо утверждением из списка предположений доказываемой цели, либо результатом одного из предыдущих шагов вывода. Тогда если утверждение ^ & ... &f_m может быть сопоставлено с условием справедливого утверждения, имеющего вид ф₁ & . & ф_т ^ ф , а 0 - наиболее общий унификатор f & ... &f m и ф₁ & ... & ф_т , то верно утверждение / , являющееся результатом применения подстановки 0 к ф (результат шага вывода ).

Цель считается доказанной, если результатом последнего шага вывода является утверждение, совпадающее с математическим утверждением цели, или синтаксически эквивалентное ему.

В случае декомпозиции цели и в выводе варианты применения Modus ponens могут быть обобщены на случай, когда импликация заменена равносильностью.

7    Формализованные способы рассуждений

Способы рассуждений, которые используются в методах доказательства, делятся на два класса :

• ■    с опорой на пропозициональные тавтологии, лежащие в основе логических рассуждений;

• ■    с опорой на математические принципы и утверждения о синтаксических преобразованиях математических выражений.

• 7.1    Язык представления пропозициональных тавтологий

Эти способы рассуждений представлены явно пропозициональными формулами, являющимися тавтологиями, и метаматематическими утверждениями соответственно. Метаматематические утверждения считаются правильными, если их достоверность установлена на основе интуитивного или конвенционального (в результате соглашения между членами математического сообщества) критерия. Таким образом, доказательство считается правильным, если признается справедливость всех используемых в нем метаматематических утверждений.

Далее описываются язык представления пропозициональных тавтологий, язык представления метаматематических утверждений, а также способы рассуждений, входящие в ядро базы формализованных способов рассуждений, и способы расширения последней.

Порождающая графовая грамматика, описывающая абстрактный синтаксис языка представления пропозициональных тавтологий, изображена на рисунке 3. Каждая пропозициональная тавтология представляется вершиной графовой грамматики « Тавтология » и имеет вид: v 1 ... v _n pf , где pf - пропозициональная формула, содержащая вхождения пропозициональных переменных v 1 , ... v_n , а v i ( i = 1, .., n ) - описание пропозициональной переменной v i , n >  1. Значением пропозициональной переменной может быть одна из логических констант - истина или ложь .

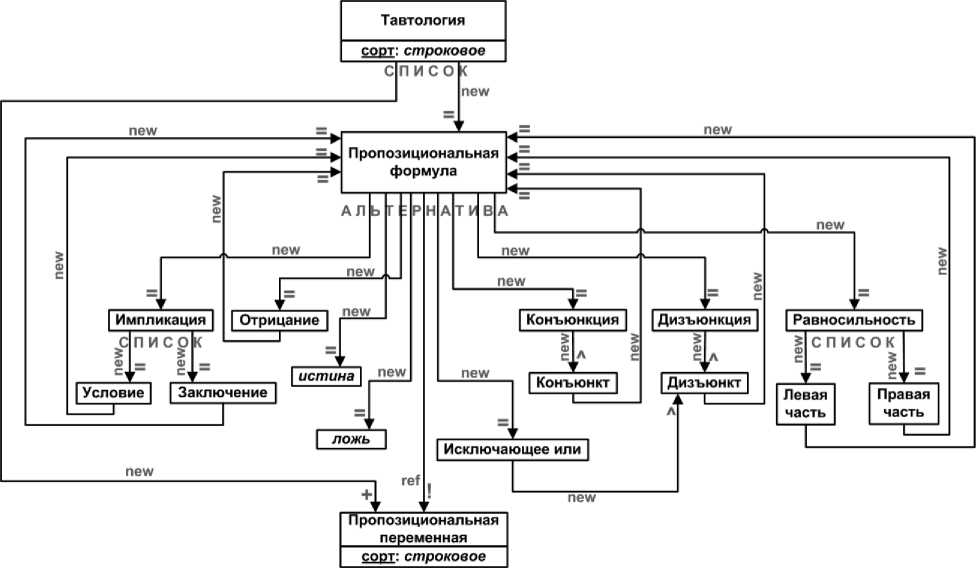
Рисунок 3 - Орграф грамматики, описывающей абстрактный синтаксис языка представления пропозициональных тавтологий

Для языка представления пропозициональных тавтологий формулируются следующие контекстныеусловия на пропозициональные переменные.

• ■    Для каждого использующего вхождения переменной в пропозициональную формулу существует определяющее вхождение этой переменной в префикс этой формулы.

• ■    Наоборот, для каждого определяющего вхождения переменной в префикс формулы существует использующее вхождение этой переменной в эту формулу.

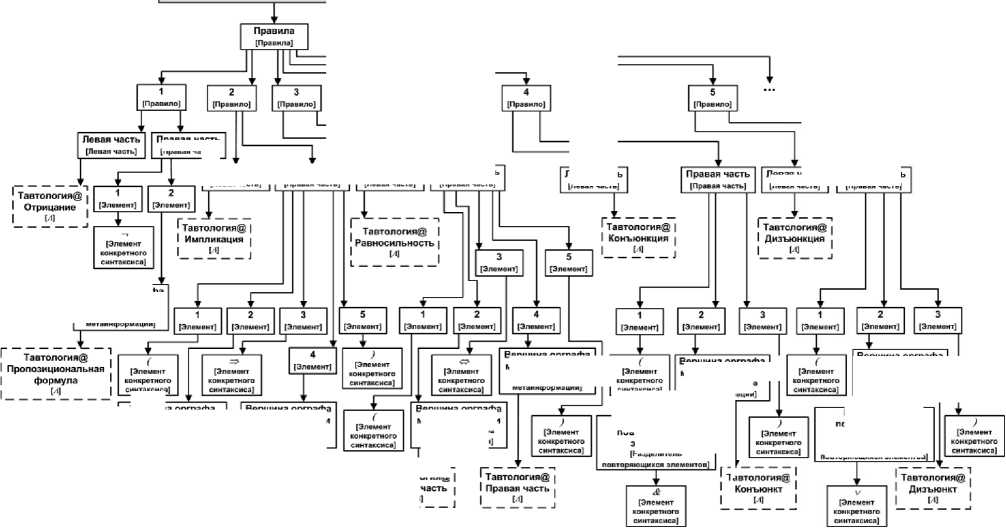
Фрагмент порождающей текстовой грамматики, описывающей конкретный синтаксис языка представления пропозициональных тавтологий, изображен (в виде орграфа информации) на рисунке 4. Всего грамматика содержит 8 правил.

Правая часть [Правая часть!

Левая часть [Левая часть]

Правая часть [Правая часть]

Грамматика языка текстового представления пропозициональных тавтологий [Язык описания грамматик]

I ___

Левая часть (Левая часть]

синтаксиса]

Тавтология® вершина орграфа метаинформации [Вершина орграфа метаинформации]

^Тавтология© | I Заключение । | И

Вершина орграфа метаинформации [Вершина орграфа метаинформации]

^Тавтология© ।

I   Условие    I

I И       I

Рисунок 4 - Фрагмент орграфа информации, специфицирующего грамматику, описывающую конкретный синтаксис языка представления пропозициональных тавтологий

Правая часть [Правая часть]

Левая часть [Левая часть]

Правая часть [Правая часть]

Левая часть (Левая часть]

Вершина орграфа мета ин формации [Вершина орграфа метаинфор м а ци и]

Вершина орграфа метаинформации [Вершина орграфа метаинформации]

Вершина орграфа метаинформации [Вершина орграфа мегаинформации]

^Тавтология© [

I Левая 1

синтаксиса]

Вершина орграфа метаинформации [Вершина орграфа метаинформации]

Разделитель повторяющихся элементов [Разделитель

Вершина орграфа метаинформации [Вершина орграфа метаинформации]

Разделитель повторяющихся элементов [Разделитель повторяющихся элементов]

• 7.2    Язык представления метаматематических утверждений

• 7.2.1    Ядро языка представления метаматематических утверждений

В данном разделе описываются ядро языка представления метаматематических утверждений и механизмы его расширения.

Порождающая графовая грамматика, описывающая абстрактный синтаксис ядра языка представления метаматематических утверждений ( метаязыка ), изображена на рисунке 5.

Каждое метаматематическое утверждение (предложение) представляется вершиной графовой грамматики « Метаматематическое предложение » и имеет вид: ( v 1 : t 1 ) ... ( v_n: t_n ) t 1 ... tk f1 ... f_s i1 ... ip r1 ... rq f. Здесь f - математическая формула, содержащая вхождения предметных переменных v 1 , .., v_n , а также вхождения синтаксических переменных t 1 , ..., t k типа t , синтаксических переменных f , . ., f s типа / , синтаксических переменных i 1 , .., i p типа i и синтаксических переменных r 1 , ., r q типа r . При этом ( v i : t i ) ( i = 1, ..., n ) - описание предметной переменной v i , t i - математический терм, значением которого является множество (область возможных значений предметной переменной v i ); t1 ... tk - описания синтаксических переменных типа t ( k >  0), значениями которых являются термы; /1 ... fs -описания синтаксических переменных типа f ( s >  0), значениями которых являются формулы; i1 ... ip - описания синтаксических переменных типа i (p >  0), значениями которых являются целочисленные константы; r1 ... r q - описания синтаксических переменных типа r ( q >  0), значениями которых являются вещественные константы; где k + s + p + q >  0.

Метаязык является надстройкой над языком представления математических утверждений и получается расширением конструкций « формула » и « терм » этого языка. Конструкция « формула » расширяется путем добавления двух альтернатив: « синтаксическая переменная типа f » и «модифицированная синтаксическая переменная типа f ». Конструкция «терм »

расширяется путем добавления четырех альтернатив: « синтаксическая переменная типа i », « синтаксическая переменная типа r », « синтаксическая переменная типа t » и «модифицированная синтаксическая переменная типа t ».

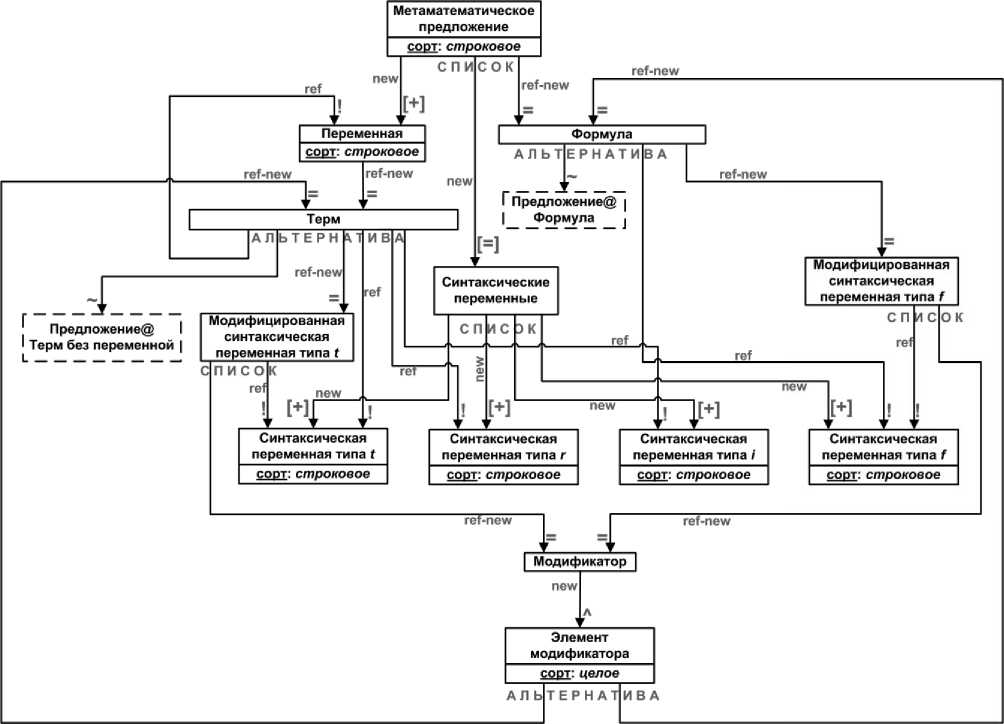
Рисунок 5 - Орграф грамматики, описывающей абстрактный синтаксис языка представления метаматематических утверждений

Модифицированная синтаксическая переменная кроме названия содержит модификатор. Она является термом или формулой в зависимости от её типа. Модификатор состоит из элементов модификатора, каждый из которых может быть термом или формулой. Значением такой синтаксической переменной является синтаксическая конструкция, соответствующая типу синтаксической переменной, но содержащая формальные параметры. Каждому элементу модификатора соответствует свой формальный параметр, который может входить в значение синтаксической переменной один или более раз. Элементы модификаторов с одним порядковым номером в разных вхождениях модифицированной синтаксической переменной в одно и то же метаматематическое утверждение соответствуют одному и тому же формальному параметру. Сами элементы модификатора являются фактическими параметрами. Значением вхождения модифицированной синтаксической переменной в метаматематическое утверждение является значение этой синтаксической переменной, в котором все формальные параметры заменены фактическими.

Метаматематические утверждения считаются справедливыми при любых допустимых значениях синтаксических (в том числе и модифицированных) переменных.

Для ядра языка представления метаматематических утверждений формулируются следующие контекстныеусловия на синтаксические переменные.

• ■    В каждое метаматематическое утверждение должна входить хотя бы одна синтаксическая переменная.

• ■    Для каждого использующего вхождения синтаксической переменной в терм или формулу метаматематического предложения существует определяющее вхождение этой переменной в префикс этого предложения.

• ■    Для каждого определяющего вхождения синтаксической переменной в префикс метаматематического предложения существует использующее вхождение этой переменной в терм или формулу этого предложения.

• ■    Модификатор модифицированной синтаксической переменной не может содержать как непосредственных, так и опосредованных вхождений этой же самой синтаксической переменной.

• ■    Синтаксическая переменная может входить в метаматематическое утверждение либо не-модифицированной, либо модифицированной (и то, и другое одновременно исключено).

• ■    Если синтаксическая переменная является модифицированной, то она должна входить в метаматематическое утверждение не менее двух раз.

• ■    Число элементов модификатора во всех вхождениях одной и той же модифицированной синтаксической переменной в метаматематическое утверждение одно и то же, причём на соответствующих местах в модификаторе должны находиться либо термы, либо формулы.

• 7.2.2 Механизмы расширения языка представления метаматематических утверждений

• 7.3 База формализованных способов рассуждений

Текстовая грамматика, описывающая конкретный синтаксис ядра языка представления метаматематических утверждений, содержит правила, относящиеся к представлению в текстовом виде немодифицированных и модифицированных синтаксических переменных.

Определение метаязыка как надстройки над языком представления математических утверждений (т.е. как его надъязыка ) является достаточным условием для того, чтобы метаязык расширялся автоматически при расширении языка представления математических знаний. Это справедливо в силу способа определения конструкций « Формула » и «Терм » метаязыка - через одноимённые конструкции языка представления математических знаний, которые расширены соответствующими синтаксическими переменными (см. рисунок 5), а также за счёт соблюдения первого контекстного условия на синтаксические переменные. Таким образом, расширение этих двух языков происходит одновременно .

База формализованных способов рассуждений состоит из множества способов рассуждений, моделируемых пропозициональными тавтологиями, и множества способов рассуждений, моделируемых метаматематическими утверждениями. В ядро базы входят следующие пропозициональные тавтологии.

• ■    Декомпозиция равносильности: ( v 1 ^ v₂ ) ^ ( v 1 ^ v₂ ) &  ( v₂ ^ v 1 ).

• ■    Транзитивность равносильности: ( v 1 ^ v₂ ) &  ( v₃ ^ v₂ ) ^ ( v 1 ^ v₃ ).

• ■    Доказательство от противного: ( ^v ^ ложь ) ^ v .

• ■    Доказательство противоречия: ( ^v & v ) ^ ложь .

• ■    Редукция импликации: ((( v 1 & v₂ ) ^ v₃ ) & v 1 ) ^ ( v₂ ^ v₃ ).

В ядро базы формализованных способов рассуждений входят следующие метаматематические утверждения (аксиомы). Имена синтаксических переменных выделены полужирным начертанием, а элементы модификатора заключены в специальные скобки “ р ” и “ ^ ”.

• ■    Рефлексивность равенства: t 1 = t 1 .

• ■    Симметричность равенства: ( t 1 = t₂ ) ^ ( t₂ = t 1 ).

• ■    Транзитивность равенства: (( t 1 = t₂ ) &  ( t₂ = t₃ )) ^ ( t 1 = t₃ ).

• ■    Принцип замены равных термов в формуле: ( t 1 = t₂ ) &  f р t 1 ^ ^ f р t₂ ^ .

• ■    Принцип замены равносильных формул в формуле: f ^ f₂ ) &  f Yf 1 d ^ fk f d-

• ■    Одна из форм принципа полной математической индукции:

⁽ v , _: 1(0. « ) ⁽ v 2 : 1[0, v , ] ) ^f k < Н &  f к ^V Hy ^{f k v} 2 + I d ) ^ ^{f k} V , d .

Кроме перечисленных, в ядро базы входят также метаматематические утверждения (аксиомы), моделирующие свойства различных кванторов, присутствующих в языке представления математических знаний.

Расширение базы формализованных способов рассуждений состоит в расширении множества пропозициональных тавтологий и/или множества метаматематических утверждений.

Множество пропозициональных тавтологий является расширяемым за счёт возможности формулировать новые пропозициональные формулы, которые в случае успешной автоматической проверки их общезначимости добавляются в это множество.

Множество метаматематических утверждений является расширяемым за счёт возможности формулировать новые утверждения, которые включаются в это множество. В частности, нужно заметить, что если в язык представления математических знаний добавляются новые кванторы, то становится необходимым добавление метаматематических утверждений о свойствах этих кванторов.

8 Модель онтологии полных доказательств

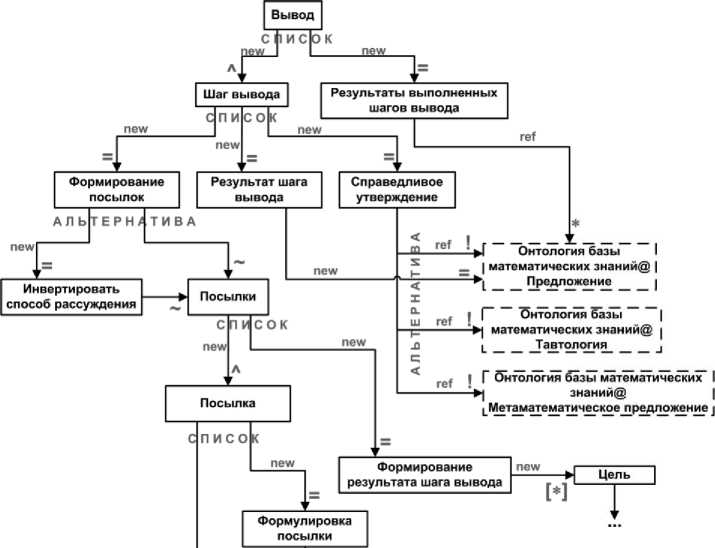
Полное доказательство является синтаксической структурой, которая представляет собой множество связанных определенным образом целей . Первой целью является доказываемая теорема / лемма , у которой список предположений отсутствует. С каждой целью связан метод её доказательства . Множество допустимых методов доказательства цели является несобственным подмножеством множества методов, описанных в разделе 6. Число методов в нём может варьироваться от трёх до пяти - в зависимости от синтаксической формы утверждения цели (имеет ли оно форму импликации или нет) и наличия или отсутствия у неё предположений. Синтаксическая структура каждого метода доказательства основана на его семантике (см. раздел 6). В случае использования правила Modus ponens для декомпозиции цели или вывода учитывается вид справедливого утверждения - импликация или равносильность - и правила выбора значений для посылок.

Синтаксическая структура полного доказательства положена в основу декларативного описания модели онтологии доказательств теорем. Орграф грамматики, представляющий собой спецификацию модели онтологии, представлен на рисунках 6-9.

Заключение

В работе представлена концепция программной оболочки для систем верификации интуитивных математических доказательств и рассмотрена декларативная метамодель для спецификации формальных логических систем, которые могут быть положены в основу такой оболочки.

С использованием этой метамодели специфицировано ядро формальной системы, приближенной к математической практике конструирования интуитивных математических доказательств, и предложены механизмы её расширения.

Разработаны и явно представлены декларативные спецификации расширяемых языков для представления математических знаний и формализованных способов рассуждений, а также модели полных доказательств. Язык представления формализованных способов рассуждений состоит из двух подъязыков: языка представления пропозициональных тавтологий и метаязыка. На первом из них представляются правила логических рассуждений, на втором - свойства логических и нелогических кванторов, а также логических и нелогических принципов.

new

Онтология доказательств

Доказываемое утверждение

СПИСОК

new

Утверждение

| Онтология базы

। математических знаний©

।____Теорема^___

V rel “

new

Доказательство сорт: строковое

| Онтология базы

| математических знаний©

।         Лемма

I Онтология базы | математических знаний© । Следствие

ref ^

ref c

new

Метод доказательства

| Цел|

all

1 ~

Г Онтология базы I

| математических знаний® |

। Предложение j

Список предположений

АЛЬТЕРНАТИВА

Не импликация без предположений Импликация без предположений Не импликация с предположениями Импликация с предположениями new

Унификация

new

Декомпозиция цели

new

Вывод ---► ■■■

new

Декомпозиция предположения new

	new	Доказательство
		импликации

| математических знаний© | । математических знаний© ||            знаний©            |

L Предложение ] L Тавтология j Метаматематическое предложение j

Рисунок 6 - Фрагмент орграфа грамматики, представляющего модель онтологии доказательств

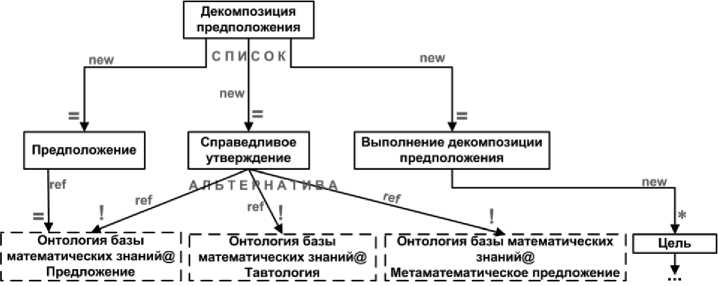
Рисунок 7 - Фрагмент орграфа грамматики, представляющего модель онтологии доказательств. Декомпозиция предположения

Декомпозиция d п и с о|к

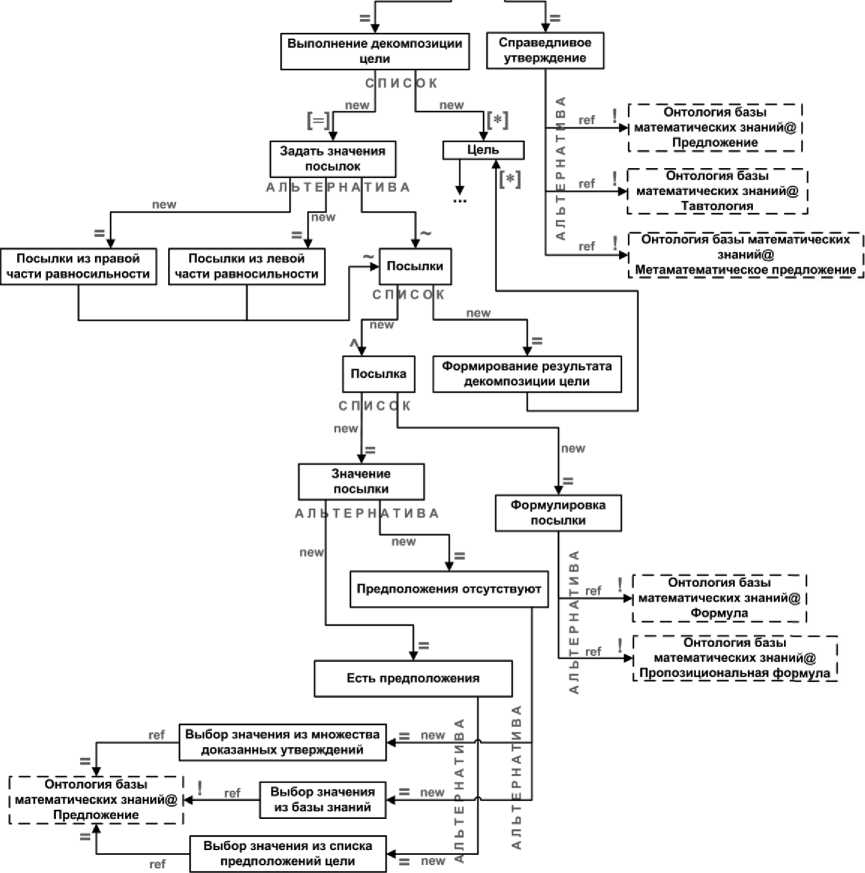
Рисунок 8 - Фрагмент орграфа грамматики, представляющего модель онтологии доказательств. Декомпозиция цели

■ Г Онтология базы I

—►] математических знаний© | Формула        ।

। Г Онтология базы ।

—►, математических знаний©

LПропозициональнаяформула *

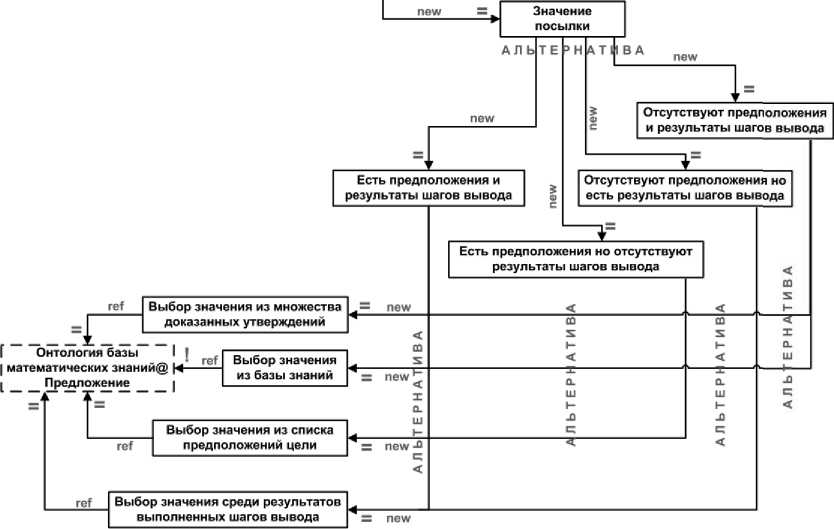
Рисунок 9 - Фрагмент орграфа грамматики, представляющего модель онтологии доказательств. Вывод

Средства расширения имеют только язык представления математических знаний. Метаязык, надстроенный над ним, в силу способа определения расширяется автоматически при его расширении. Язык представления пропозициональных тавтологий расширяемым не является. Расширяемость языка представления математических знаний обеспечивается расширяемостью множества определений, позволяющих вводить новые термины для обозначения определяемых понятий (внутренние средства расширения), а также расширяемостью его грамматики (внешние средства расширения). Расширяемость грамматики достигается благодаря средствам, позволяющим описать синтаксис новых конструкций языка представления математических утверждений, а также, при необходимости, контекстные условия. Исчисление, в рамках которого строятся доказательства, представлено явно и является расширяемым.

Полученные в ходе исследований результаты могут быть использованы в проекте по разработке QED2-системы и в проектах управляемых интерактивных СППД теорем, являющихся приближениями к этому проекту.

Работа выполнена при частичной поддержке РФФИ (проекты 16-07-00340, 17-07-00299 и 18-07-01079).