Теоретические основы применения прямого и обратного преобразования Лапласа к телеграфному уравнению

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 519.633                                        

Численные методы обращения преобразовании Лапласа наиболее полно описаны в работе [1].

В работах Н. И. Порошиной, В. М. Рябова [2, 3] изложены о методах обращения преобразования Лапласа и их сравнения для некоторых специальных функций.

В диссертационной работе Н. И. Лещенко разработаны и исследованы приближенные методы обращения преобразования Лапласа к изображениям функций специального вида и они использованы для нахождения напряжения и деформации вязкоупругих материалов [4].

В статье рассмотрено практическое приложение метода обращения преобразования Лапласа и предложена интегральная модель теплопереноса и разработан численный метод определения температуры [5]. Здесь с помощью преобразования Лапласа задача сводится интегральному уравнению Вольтерра, характеризующему прямую зависимость неизвестной граничной функции от исходных данных.

Авторами Н. Н. Яремко, В. Д. Селютина и Е. Г. Журавлева в работе получены новые формулы для прямого и обратного интегрального преобразования Фурье, двухстороннего преобразования Лапласа, которые могут быть основой для создания устойчивых вычислительных алгоритмов [6].

Необходимо отметить, что здесь формулы обращения интегральных преобразований Лапласа не содержат производных. А состоят из системы ортогональных полиномов Эрмита.

В книге крупного математика профессора Фрейбургского университета Густава Деча рассмотрено практическое применение преобразования Лапласа в широком смысле, для задач математики и техники [7]. Изложено также Z-преобразования и его применения к импульсным системам.

Материал и методы исследования

Во многих задачах дифференциальных уравнений (ДУ) и ДУ в частных производных, физики и механики, астрофизики и геофизики решение ищется с применением преобразования Лапласа. Основным затруднением применения преобразования Лапласа, особенно при решении уравнений математической физики, состоит в том, что при нахождении функции оригинала по ее изображению невозможно решить аналитически, т. е. в этом случае необходимо разработать численные методы решения. Отметим, что не существует общий численный метод обращения преобразования Лапласа, т. е. для каждой задачи разрабатываются свои численные решения, учитывающие специфику задачи и функции оригинала. А именно от изображения искомого оригинала зависит выбор численного решения задачи.

Метод интегральных преобразований является одним из наиболее действенных методов решения модельных задач математической физики, техники, фильтрации сигналов. В перечисленных источниках о преобразованиях Лапласа мы не нашли о применении обращения преобразовании Лапласа к задачам телеграфного уравнения гиперболического типа и параболического типа с мгновенным источником и плоской границей. Применения преобразования Лапласа к указанным задачам возникли при решении прямых и обратных задач телеграфного уравнения гиперболического и параболического типов [8–12].

В данной статье осуществлено применение преобразования Лапласа к этим задачам и теоретически обосновано при определенных условиях. Применение преобразования Лапласа к решению гиперболических и параболических задач имеет ряд преимуществ от классических методов интегрирования вышеуказанных задач.

Первое преимущество — это оно однотипно, способ решения прямая.

Второе преимущество — оно имеет в хорошем решении при начальных и граничных условиях.

Третья — для многих задач оно имеет много подробных готовых таблиц изображений.

Результаты и обсуждение

Постановка задачи. При доказательстве существовании, единственности решений, а также при численных решений прямой задачи (конечно-разностным методом), при численных решений обратных задач (конечно-разностным регуляризованным методом) обобщенных задач распространения потенциала действий по нервному волокну телеграфного уравнения:

параболического типа:

'            r a ( x )                 u ( x , t )                 2

C m ⁽ xu t ⁽ x ’ t )             \ u xx ⁽ x , t )           \j ’   ⁽ x ’ t ⁾⁶ R + ,

2Pa (x )           Pm (x)l

U(x ’ t ) t <0 = 0,    ux (x, t )    = h 0^(t ) + rO^l (t)+ P 0^2 (t X x=0

^{u ( x} , t ) _x =₀ = g ^{( t} \ t 6 [ 0, T 1

гиперболического типа:

C_mV tt ( x , t ) =

ra (x ) 2Pa (x)

ip ( x , t ) - xx

V ( x , t ) P m ⁽ x ) • ^l ’

( x , t ) e R ²,

^{V ( x} , t ) t < 0 "  0,

d V ( x , t )

S x

= h 0 ^ ^{( t )+} r 0 ^{0 ( t )+} P 0 ^ 1 ^{( t} )

x = 0

V ( x , t ) x = 0 = f ( t ) t e [ 0. T J                                              ⁽⁶⁾

где h ₀, r ₀, p₀ — заданные положительные числа, C_m ( x ) — емкость на единицу площади мембраны, r_a ( x ) — радиус нервного волокна, p _m ( x ), р ( x ) — удельное сопротивление плазмы и нервного волокна, l — толщина мембраны, a , m — индексы аксоны и мембраны, u ( x , t ) — внутриклеточный потенциал действий, 0 ( t ) — тета функция Хевисайда, ^ ( t ) — дельта функция Дирака, V ( x , t ) — скорость внутриклеточного потенциала.

Связь между решениями задачи параболического типа (1)–(3) и гиперболического типа (4)–(6) преобразованием Лапласа:

ГС

u ( x , t ) = j V ( x ,т )G_t J t ,т ) dr, 0

rc

g(t ^f f (t )Gtt(t ,T)dT, где G(t,t) = —^=-exp(r2/41) — функция Грина. V nt

Целью данной статьи является теоретически обосновать обращения преобразования Лапласа (7) и (8).

Отметим, что формулы (7) и (8) устанавливают взаимнооднозначное соответствие между решениями (1)–(3) и (4)–(6). Отсюда следует, что теоремы единственности и устойчивости, обоснованные для коэффициентных обратных задач (4)–(6) могут быть перенесены на соответствующие коэффициентные обратные задачи (1)–(3).

Формула (7) является прямым преобразованием Лапласа. А обратным преобразованием Лапласа будет:

1   ст +«

V ( x , t ) =        u ( x , t G_tttt , t )dT,

2n с-TO

где с — некоторое вещественное число.

При численных решениях часто используют дискретные преобразования Лапласа

TO ud (x,t)= Еu(x,пт)^(t - пт), п=0

где п т — дискретные моменты времени, п — целое число, т — период дискретизации. Тогда D — дискретное преобразование Лапласа будет:

то

D fa ⁽ x , t ^)}= Е u ⁽ x , ^{п т} ) • G tt ^{( t} , ^пт \ п = 0

Обратное преобразование Лапласа (9) существует при следующем достаточном условии:

Если изображение u ( x , t ) аналитичная при с >  с_а и имеет порядок меньше Л, то обратное преобразование Лапласа существует и непрерывно для всех значений аргумента и L { u ( x, т )} = 0, при т <  0.

Покажем связь задачи (1)–(3) и (4)–(6) по преобразовании Лапласа (7) и (8).

Предположим, что коэффициенты уравнений r_a ( x )/( 2 p ( x ) • C_m ( x )) , 1/ ( l • p _m ^{( x} ) • C m ^{( x} ))

растут не быстрее чем функции Ce ^at при t ^ то , где C , а — положительно-постоянные и

то

g ⁽ t ) = f fТ ) G ⁽ t , т ) dт, G ( t,т ) = -j=e о                     ПЖ

_ Т2

.

Тогда проделаем следующие выкладки то                                                               TO u (x, t ) = f V (x ,т )Gt (t ,т )dT = Gt = GTT\ = f V (x ,т )GTT (t ,т )dT = V (x, t )GT (t ,т ) -V (x, t )G (t ,т ) +

0                                                 0

+ f V _TT ( x , т ) G ( t , т ) dT = f V _TT ( x , т ) G ( t , т ) dT.

r _a ( x )          "                  1

( 2 P a ( x ) C m (. x )) “ xx ⁽ x ’ ‘ ^)— l • p m ( x ) C m ( x ) ^ u ⁽ ' ’ ‘ ’ =

то

то

- то        r a ⁽ x )       V Л

= ^f ^ ( 2 P a ( x ) ■ C m ( x )) V ’ ⁽ x ’ ^T ’

то

—

----- ¹       V ^{( x, T} ) ^{G ( t, T} dT = ^l • P m ^{( x}C m ^{( x} )        J

^то          r ( x )              "                           ^то            1

= ^f ( 2 _{P a} ( x ) • C m ( x )) ^V x ⁽ x , ^{T) G (} t ^T ) d ^T -^f iPjxCM ^{V (} x ’^ ⁽ t ' ^T

Отсюда, при t g R+ получим u (x, t)-

( 2 P a ( Х К ( x )) u x ⁽ x ’ ^{t )-} l • P m ( xC ( X ) • ‘‘ ⁽ ' ’ t ) =

К

=JV(x ,т ) 0 .

-

____(aW____I/ ”

( 2 P a ( X C ,, ( X )) ^{V   ( X} • ^T)

V (x ,т )

¹ • P m ^{( X ) C}m ^{( X} )

G ( t , т ) dт,

КCO

V ( 0,2 4tr e ^т dr = V ( o, t ) = g ( t ).

u (0, t) = lim  V (0, т )G (t, т) dr = lim —= [ t ^0

Таким образом, от параболического уравнения можно получить гиперболическое уравнение.

На практике часто используют Z — преобразования Лапласа.

К

Z { u _z ( X , t )} = ^ u ( x , n ?C_tt (t , n т ).

n = 0

Если интеграл Лапласа абсолютно сходится при точке а = а0, то существует предел b                         к lim JV(x,т)CtC,т)dт = JV(x,т)CC,т)dт.

0                               0

Тогда интеграл Лапласа (9) сходится абсолютно и равномерно для а >  а₀ и а— действительная часть.

Прямое преобразование Лапласа (7) существует при следующих случаях:

• 1.    Преобразование Лапласа существует если существует интеграл

• 2.    Преобразование Лапласа существует, если интеграл   J V ( x,т )| dr существует для

• 3.    Преобразование Лапласа существует, если существует преобразование Лапласа для функции V ( x , т ) для а >  0.

К

J V ( x ,т ) dr , 0

О существовании решения V ( x , t ) — нами доказано в статье [9].

^т 1

каждого конечного т >  0 и V ( x, т ) <  ке ^а“^т , для т >  т ₂ >  0.

Достаточное условие преобразования Лапласа:

• 1.    Для любого положительного T функция V ( x , t ) — кусочно непрерывная функция на интервале t g [ 0, T ], x g R₊ .

• 2.    Существуют положительные числа ^ , T и а , что V ( x , t ) <  p e ^a , V t >  T .

К

Тогда преобразование Лапласа L [ V ( x , t ) ] = F [ u ( x , s ) ] = J V ( x , t ) e - ^stdt существует при всех 0

s >  а . В формуле (7) u ( x , t ) — изображение, а V ( x , t ) — оригинал.

Оригинал V ( x , t ) удовлетворяет следующие три условия:

• 1.    V ( x , t ) = 0 при t <  0, первая формула (5),

• 2.    V ( x , t ) удовлетворяет условию Липщица-Гельдера:

• 3.    Функция V ( x , t ) возрастает не быстрее показательной функции Грина G ( t , т ).

V t > 0 3 A > 0 и Ba :0 < a < 1 и 3 h > 0 |V (x, t + h)-V (x, t )< A\h\a, где h — шаг сетки, а у нас A = exp

2 - + h² d

s

С физической точки зрения и процессов последнее условие всегда справедливо. Дифференцирование изображения:

u ^{( n} ) ( x , t ) = ( - 1 ) ⁿ • V ( x , t )

Интегрирование изображения:

u^ = J L { V ( x , t )} dr t       0

t

L { u ( x, t )}

.

t

Интегрирование оригинала: j V ( x , t ) dr =

Прежде всего, для того чтобы применить прямое преобразование Лапласа для обратной задачи параболического уравнения (1)–(3) и обратное преобразование для обратной задачи гиперболического уравнения (4)–(6) устанавливаем некоторые утверждения.

Теорема 1. Пусть f1 (t), V(x, t)g L(0, то), Vx g R и ее преобразования Лапласа равно то                                                                то

F [ u ( x , p ) ] = j V ( x,т ) • G tt ( x , t ) dr,  F [ g ( p ) ] = j f ( t ) G _tt( t , t dr, G ( t , t ) = exp (r ²/4 1 ) • [ - 1/ П а ] .

0                                                  0

Тогда для любого t >  0 имеет место формула обращение

( - 1 ) ⁿt^{n - 1} n! ( n - 2)!

то

V (x, t )= lim n >то

j G (t, p) p2 n-1F(n )[u (x, p)] dp, n n-1 то

^{f ( t} ) = lim            I G ^{( t} ’ p ) p^{2n - 1 F ( n )[} g ⁽ p ^)] dp .

ⁿ •' n ! ( n - 2 )!

Теорема 2. Если V(x, t), f (t) имеют ограниченную вариацию на отрезке [0, T] при T > 0 то                                                                    то и интегралы j V(x,т )Gt (t ,t ) dr = F [u (x,p)] и j f (t)Gt(tt,t)dr = F[g(p)] абсолютно сходятся 00

при некотором p, то lim -—— tn+1F(n)[u(x, pn)] = — [u(x, t + 0)+ u(x, t - 0)], n >' n!2

lim t11:+1 f (• >[g (pn)] = 1 [f■ (t + 0)+f (t - 0)], n >' n!2

f (t) = lim fn (t), u (x, t) = lim un (x, t), n >то                    n >то то fn (t)   t(n - 2)

₍ j ^{F [} g ⁽ p ^T ) • ^G tt ^{( t} ’ ^T ) p^{n - 1} L n ⁽ p ’ ^{n - 1} )^{] d T} -

^! 0

Доказательство теоремы 1 и теоремы 2 можно найти в [13, 14].

Для применения обратного преобразования Лапласа [15, с. 69] к параболической задаче (1)–(3), обозначим

r (x )                          1

( x ) =     -        ,   b ⁽ x ) =                 (для сокращения)

2P- (xCm (x)          Pm (xГ l • Cm (x)

TO u (x, p ) = J V (x ,T CT (x,pr) dr.

Применяем преобразования Лапласа по t к уравнению (1)

p • u = c2 (x)  u — 0(xU = 0, dx2

Общее решение уравнение имеет вид px

u ( x , p ) = Ae ^-  + Be

px a

, при p ^ to , B = 0.

du ( x , p ) dx

—A

x = 0

b

x e^a

_ c(0)(h0^(0) + rX0) + p0^,(0))

x = 0

p^p+0 (0)

;

Отсюда A = —

b (0)

CP + bC)

* c(0)[h0^(t)+ rAp)+ p0^1(p)]

*-------------.      =---------

p^p + b (0)

.

Известно, что

e

V nt

T 2

4 t

e ^ ^T

e^c . Тогда

т ²

= —7=e ^{4 ct} . С учетом смещений

c

p+Cb

J p + 0 -------т

c

c

=  - e d nt

T ²

^{4 ct} • e

u

p

p

nt

- ct

.

t

_ T ²

_e 4 ct _e

—

^{c T} • V ( x , t ) dr .

Применим преобразования Лапласа [16, с. 323] к задаче гиперболического уравнения (4)–(6). Для численного решения обратной задачи гиперболического типа решения (4)–(6) представим в виде:

V (x, t) = A • exp

— x-J c ² ( x ) b ² ( x ) — a ² — i at

Решение уравнения с неоднородным граничным условием будет

G ( x ,0, a ) =------- , c ⁽ x )          • exp

c2 (x) p2 + c2 (x )b (x)

— xjp² + 0 ² c² c

p = ia.

По таблице преобразования Лапласа находим импульсную функцию (х=0):

G (x ,0, t ) =

c (x) J0

0,

c (x ) • 0 (x ) д/12 — (x/c )2

x

t > -

c

x

t < -

c

Тогда решение (4)-(6) выражается интегралом (вместо  c(x) и 0(x) ставим свои значения)

t - у c

V ( x , t )=-p- j u ( x ,T ) • J о

c ^{( x} ) 0

X J

rlx)

----------7---7-----------7---Г •

\ 2 Pa (x )• Cm (x )

c ⁽ x b ⁽ x ^/( t - ^ F-f xC ) ²

dr =

2pa (x )Cm (x ) t—Xcz .

Pa' m       u (x ,T)x ra (x )       0

P m ⁽ xCm ⁽ x )

(t — t )2

(

. 2 £ a (xC m ( x )' Г а ⁽ x )     ,

dT.

Интеграл проводится до t —

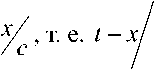
ra (x )

\ ² Pa ⁽ x ^{) C}m ⁽ x ) .

Вывод

Таким образом, в данной статье обосновано применение преобразования Лапласа к обратной задаче телеграфного уравнения параболического типа и обратное преобразование Лапласа к обратной задаче телеграфного уравнения гиперболического типа. Более того, что единственность и устойчивость решения обратной задачи гиперболического уравнения эквивалентно единственности и устойчивости решения обратной задачи параболического уравнения.