Теоретическое и экспериментальное обоснование целесооб-разности сушки дисперсных материалов при осциллирующем теплоподводе

В [1] построена модель процесса конвективной сушки капиллярно-пористых тел в режиме осциллирования.

Окончательная формулировка математической модели конвективной сушки капиллярно-пористого тела при осциллирующем режиме изменения температуры сушильного агента:

Pp      2 R ² u 1 R U )

_ pLu   7+

R Fo       (R R² R R R J

p LuPn _P

2 R2T 1 RT) v RR2 + R RR v

+

+ (Lu _P

-

U _т 2 Uu 1 R U )

= Lu    +

FOo   ( RR² R R R J

P uPn p ) R- 2 + ^ R R

1 RP) R RR J

+

начальные условия

+ LuPn

2 R2T 1 RT) v RR2 + R RR v

+

U ( R ,0) = T ( R ,0) = P ( R ,0) = 0,

условия осесимметричности

+ LuPn _P

2 R2 P 1 RP) v RR2 +R RR v

R U (0,Fo) _ R T (0,Fo) _ R P (0,Fo) _ 0

R R ” R R ” R R ~

условия на внешней границе

TT

R Fo

FeLu 2 R ² U 1 R U )

Pn

_v R R^{2 +} R RR ,

+

_c . 2 R ² T 1 R T ) +(1 +FeLu) —7+—— +

( R R ² R R R J

FеLuPn

+------ P

Pn

2 R ² P 1 R P ) _vR R ^{2 +} R R R J ,

d U (1,Fo) + Pn R T (1,Fo) +

R R         dR

+ Pn p ^Fo) + Bi m [ U (1,Fo) - 1 ] _ 0, R R

-^^(^iFo) + Bi q [ Ф (Fo) - T (1, Fo) ] -R R

- (1 - £ )Bi m KoLu [ U (1, Fo) - 1 ] = 0, P (1,Fo) = 0;

Ф (Fo) = B + A cos( C Fo);

A = 2(1 - 1 0 / 1 c ),

B _ 2(1 + 1 0 / 1 c ),

C = 2 ^F 0² /( T, a_q ),

где U – влагосодержание, кг влаги/кг сухого вещества; P – давление влажного воздуха в капиллярно-пористом теле, Па; t – температура, К; t ₀ – начальная температура материала, К; t _c – температура окружающей среды, К; a _q – коэффициент температуропроводности материала, м²/с; r – координата, м; r ₀ – эффективный радиус капиллярно-пористого тела, м; ε – коэффициент диффузии парообразной влаги во влажном теле, м²/с; Lu – критерий Лыкова; Pn – критерий Поснова; Pn _p – фильтрационный критерий Поснова; Fe – критерий Фёдорова; Fo – теплопроводный критерий Фурье; Bi _q – теплообменный критерий Био; Bi _m – массообменный критерий Био; Ко – критерий Коссовича.

Нами выбрано численное интегрирование уравнений математической модели, основанное на конечно-разностных представлениях.

Ниже проанализированы графические зависимости, отражающие специфику сушки хлебопекарных дрожжей в псевдоожиженном слое (рис. 1) и с осциллирующим теплоподво-дом (рис. 2).

ф а о L—11-------

80 Fo

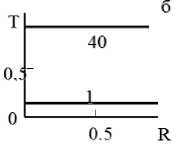
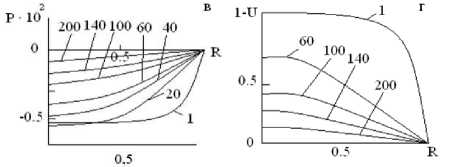
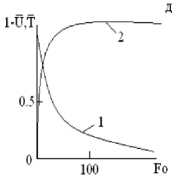
Рис. 1. Конвективная сушка капиллярно-пористого тела без осциллирования температуры сушильного агента при различных числах Fo : а – закон изменения температуры сушильного агента Φ = 1 ; б - поле температур; в – поле давления; г – поле влагосо-держания; д – интегральная характеристика процесса ( U , T - средние по объему влагосодержание и температура)

Вначале была проведена серия экспериментов при постоянной температуре подаваемого сушильного агента (рис. 1, а ). При этом, как видно из рис. 1, б , прогрев частиц практически достигает температуры сушильного агента уже при Fo ≈ 40 . Среднеинтегральная величина влагосодержания достигает величины ≈ 0,42 (рис. 1, д ). Дальнейшее проведение процесса нецелесообразно из-за перегрева дрожжей.

Из рис. 1, в следует, что на всем протяжении процесса создается антиградиент по фильтрационной составляющей парообразной влаги, препятствующий ее переносу к поверхности межфазного влагообмена (рис. 1, г ). Результаты вычислительного эксперимента в этом случае показывают, что проведение процесса сушки при постоянной температуре сушильного агента может снизить качественные показатели готовой продукции. Поэтому вычислительные эксперименты были продолжены с целью теоретического подтверждения эффективности осциллирующего закона изменения температуры сушильного агента в процессе. Такие вычислительные эксперименты имеют над собой физическую базу – из-за конечной скорости релаксации температурного поля капиллярно-пористого тела возможно подобрать такую частоту осциллирования, которая не приведет к нежелательному перегреву материала.

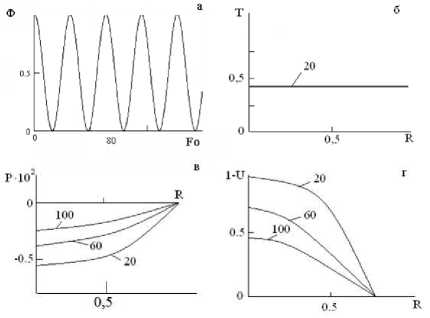
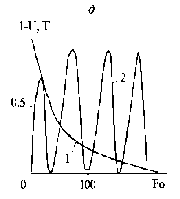
Рис. 2. Конвективная сушка капиллярно-пористого тела с осциллированием температуры сушильного агента при различных числах Fo : а - закон изменения температуры сушильного агента; б – поле температур; в – поле давления; г – поле влагосодержания; д - интегральная характеристика процесса ( U , T - средние по объему влагосодержание и температура)

На рис. 2 показаны результаты вычислительного эксперимента, когда частота осцил-лирования невелика:

Ф (Fo) = 2 [ 1 + cos ( 0,1 . Fo ) ] .

Характер изменения полей температуры (рис. 2, б ), давления (рис. 2, в ), влагосодержа-ния (рис. 2, г ), кривой сушки (рис. 2, д ) остался прежним, но среднеинтегральная температура (рис. 2, д; кривая 2) уже не достигает температуры сушильного агента на всем протяжении процесса. Таким образом, означенная выше гипотеза подтверждается, то есть возможно управление температурным режимом термолабильного капиллярно-пористого тела.

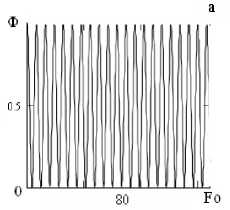
Рис. 3. Кинетика конвективной сушки капиллярнопористого тела с осциллированием температуры сушильного агента: а – закон осциллирования; б – 1 – кривая сушки; 2 – средняя температура

0           100 Fo

Следующая схема вычислительных экспериментов была ориентирована на поиск оптимального режима частоты осциллирования. На рис. 3, а показан закон осциллирования, удовлетворяющий формуле

Ф (Fo) = 2 [ 1 + cos ( 0,8 . Fo ) ] .

Следует отметить, что диапазон изменения при этом существенно сократился, хотя с увеличением Fo тенденция возрастания остается. Кроме того, по сравнению, когда ф = 1, в первом периоде сушки (Fo <  20) съем влаги в оптимальном режиме осциллирования выше примерно на 10 %.

Аналогичные результаты получены при сушке свекловичного жома в псевдоожиженном слое при осциллирующем теплоподводе.