Теоретическое использование EMD PWVD для преобразования непрерывных сигналов

Преобразование сигналов – важный этап их подготовки к дальнейшему анализу и использованию человеком или компьютером, например, такими методами, как кратковременное преобразование Фурье (далее – STFT) и вейвлет-преобразование. Их результаты позволяют представить временной сигнал в частотно-временной области как спектрограммы или скалограммы, на которых удобно искать, например, признаки дефектов при анализе виброакустических сигналов во время вибродиагностики.

В связи с этим в статье “Intelligent Fault Diagnosis of Rolling Bearing Using FCM Clustering of EMD-PWVD Vibration Images” ее автор Хонгвей Фан рассматривает метод обработки сигнала EMD PWVD, являющийся результатом объединения двух методов – EMD и PWVD. Этот метод позволяет представлять сигнал с высоким разрешением в частотно-временной области, одновременно избавляя результат от артефактов, присущих методу PWVD.

Однако метод, предложенный Хонгвеем Фаном, предназначен для анализа дискретных сигналов, что делает его полезным в основном для периодической вибродиагностики. Использование этого метода для преобразования непрерывных сигналов, в том числе в области вибродиагностики, требует совершенствования.

Целью статьи является определение возможных путей использования EMD PWVD для преобразования непрерывных сигналов и анализ возможных трудностей и артефактов при использовании метода.

Теоретическое использование EMD PWVD для преобразования непрерывных сигналов

Алферов Никита Сергеевич аспирант кафедры инструментального и прикладного программного обеспечения, МИРЭА – Российский технологический университет, Москва. Сфера научных интересов: нейронные сети, машинное обучение, вибродиагностика. SPIN-код: 5275-0880.

Что такое EMD PWVD

EMD PWVD – метод преобразования сигналов, основанный на использовании сразу двух методов преобразования сигналов – декомпозиции эмпирических мод (англ. Empirical Mode Decomposition, сокр. EMD) и псевдопреобразования Вигнера-Вилля (англ. Pseudo Wigner-Ville Distribution, сокр. PWVD). Перед рассмотрением теории работы EMD PWVD познакомимся с теорией работы двух его составляющих методов.

Декомпозиция эмпирических мод (EMD)

EMD [1] – метод разложения сигналов на функции, получившие название «эмпирических мод». EMD позволяет декомпозировать сигнал в набор функций внутренних мод (далее – IMF), где каждая IMF – отдельный компонент амплитудной/частотной модуляции сигнала [2]. Это основано на трех предположениях:

• 1)    у сигнала есть как минимум два экстремума;

• 2)    характерный масштаб времени определяется временным промежутком между последовательными чередованиями максимумов и минимумов сигнала;

• 3)    если у сигнала нет экстремумов, но есть точки перегиба, его можно продифференцировать от одного до нескольких раз, чтобы проявить экстремумы.

IMF должны удовлетворять следующим двум условиям:

• •    во всем наборе данных количество пересечений нуля и количество экстремумов должны быть одинаковы или различаться не более чем на единицу;

• •    в любой точке среднее значение между верхней и нижней огибающими равно нулю.

Вначале для сигнала x ( t ) определяются все точки экстремума, после чего высчитываются верхняя ( x _max ( t )) и нижняя ( x _min ( t )) огибающие c помощью интерполяции сплайном третьего порядка. После этого высчитывается m ( t ) – среднее значение между верхней и нижней огибающими – и h ₁ ( t ) – разница между x ( t ) и m ( t ):

,А [ x max ( E ) + x min( t)] m(t ) =  -------------------1, h1(t) = x(t) - m1(t) .

Затем h ₁ проверяется на предмет соответствия критериям IMF. Если h ₁ соответствует критериям IMF, то она принимается за с ₁ – первую компоненту сигнала x ( t ). Если нет, то вышеприведенные шаги повторяются, причем h ₁ принимается как исходный сигнал:

^h 11 ^(t ) = ^h 1 ⁽ t ) - m 11 ⁽ t )•

Эта операция может повторяться n раз, до тех пор, пока h _1n не будет удовлетворять критериям IMF.

После успешного процесса отсева получена первая компонента с ₁ , которую можно определить как

^C 1 = h l n •

Затем необходимо отделить c ₁ от оригинального сигнала x ( t ):

Г 1 = X ( t ) - C 1 •

После этого r ₁ считается за оригинальный сигнал, и по отношению к нему повторяется вышеописанный процесс. Этот процесс можно повторять m раз до тех пор, пока r _m не станет монотонной функцией. После этого процесс декомпозиции завершается.

Таким образом, оригинальный сигнал x ( t ) является суммой своих IMF и остаточной функции:

m x ^{( t} ) = ^ ^c j + r m • j = 1

Псевдопреобразование Вигнера – Вилля (PWVD)

Преобразование Вигнера – Вилля (далее – WVD) – билинейное частотно-временное преобразование, которое можно определить как преобразование Фурье центральной ковариационной функции сигнала (см. Рисунок 1) [3]. Для постоянного сигнала во временной области WVD можно представить как [4]

to

W ( t , f ) = x ( t + ^T )x( t — ^T ) e j 2 ” ^{f T} T .

Это распределение обладает высоким разрешением в частотно-временной области [5], однако поскольку преобразование Вигнера – Вилля билинейно, оно может приводить к появлению отрицательных значений и перекрестных членов в частотно-временной области, вследствие чего возможна неоднозначная интерпретация результатов преобразования. Хотя WVD выигрывает в разрешении у преобразования Фурье и вейвлет-преоб-разования, его природа приводит к появлению артефактов в итоговом результате.

Стоит заметить, что на практике WVD используется для сигналов с ограниченной длительностью. Для этого применяется псевдопреобразование Вигнера – Вилля (далее – PWVD). Это преобразование можно охарактеризовать как преобразование Вигнера – Вилля для сигнала, ограниченного оконной функцией.

Разрешение во временной области зависит от интервала сэмплирования, а разрешение в частотной – от длины окна.

Борьба с перекрестными членами, возникающими при WVD, довольно сложна, однако было предложено несколько модификаций, позволяющих улучшить производительность и повысить контроль над перекрестными членами, в частности сглаженное псевдопреобразование Вигнера – Вилля (далее – SPWVD) [3].

Теоретическое использование EMD PWVD для преобразования непрерывных сигналов

Рисунок 1. Преобразование Вигнера – Вилля. В центре можно заметить артефакт Источник: [3].

Smoothed Pseudo Wigner-Ville Distribution

Time

Рисунок 2. Сглаженное псевдопреобразование Вигнера – Вилля

Источник: [3].

EMD PWVD

Хонгвэй Фан и коллеги в статье [4] (см. Рисунок 3) приводят новый способ представления вибрационных данных, комбинируя метод EMD и псевдопреобразование Вигнера – Вилля. Поскольку теории EMD и PWVD были проанализированы в данной статье выше, в этом разделе они приводится не будут.

Чтобы избавиться от проблемы перекрестных членов при псевдопреобразовании Вигнера – Вилля, в работе [4] предлагается EMD PVWD. Для сигнала x ( t ) EMD PVWD будет

∞

∫ fPW_{IMF 1} ( t , f ) n

-∞

EMD _ PW ( t , f ) =∑              ,

^{_ x}         t = 1 PW IMF ₁( t , f )

где EMD_PWVD декомпозирует многокомпонентный сигнал в один компонент и конеч-

ную сумму функций внутренних мод (IMF), затем над каждой функцией производится

PVWD, после чего результаты преобразования накладываются, чтобы получить распределение вибрационных сигналов в частотно-временной области. Как отмечают авторы, подобная комбинация методов позволяет эффективно избавляться от перекрестных членов PVWD, сохраняя при этом его точность в частотно-временной области.

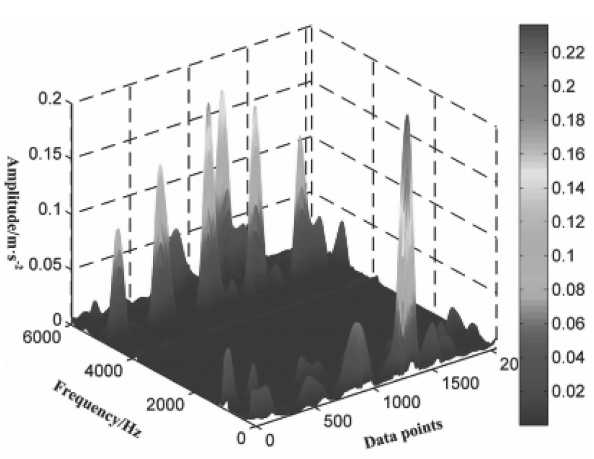
Рисунок 3. 3D-график частотно-временной области, полученный с помощью EMD PWVD Источник: [4].

Использование EMD PWVD для преобразования непрерывных сигналов

Описанный выше метод подходит для преобразования дискретных сигналов, однако не подходит для преобразования непрерывных сигналов. Для решения этой задачи необходимо создать алгоритм, использующий EMD PWVD для преобразования семплов сигнала и выводящий финальный результат как последовательность результатов преобразования этих семплов.

Далее предлагается возможный алгоритм непрерывного преобразования сигналов с использованием EMD PWVD и языка программирования Python:

1) создать массив EMD_PWVD длиной l, являющийся финальным результатом работы алгоритма и заполнить его нулевыми значениями;

• 2)    получить семпл сигнала длиной δ t , где δ t равен   , где f _s – частота семплирования;

• 3)    применить EMD PWVD к семплу сигнала, получив результирующий массив EMD_

PWVD _i , где i – порядковый номер семпла;

• 4)    сдвинуть массив EMD_PWVD влево на δ t ;

• 5)    получить срез массива EMD_PWVD [–δ t :];

Теоретическое использование EMD PWVD для преобразования непрерывных сигналов

• 6)    заполнить значения среза массива EMD_PWVD [–δ t :] значениями из массива EMD_PWVD _i ;

• 7)    вернуться к шагу 2.

Другой возможный алгоритм заключается в применении EMD PWVD для всего сигнала, находящегося в пределах оконной функции:

• 1)    первый шаг идентичен прошлому алгоритму;

• 2)    сдвинуть оконную функцию w ( t ) по входящему сигналу на δ t ;

• 3)    произвести EMD PWVD над сигналом, ограниченным оконной функцией, получив массив значений EMD_PWVD _i , гдe i – порядковый номер итерации;

• 4)    получить массив x , где x – срез массива EMD_PWVD _i [-δ t :];

• 5)    сдвинуть массив EMD_PWVD влево на δ t ;

• 6)    заполнить срез массива EMD_PWVD[-δ t :] значениями из массива x ;

• 7)    вернуться к шагу 2.

Какой из этих алгоритмов является более эффективным с точки зрения количества выполняемых вычислений, с точки зрения наглядности, точности выходных данных и наличия в них артефактов, необходимо выявлять дальнейшими экспериментами.

Возможные артефакты

Тем не менее уже возможно предсказать появление некоторых артефактов при выполнении любого алгоритма. Природа этих артефактов заключается в особенностях метода EMD, а именно в количестве итоговых внутренних мод.

При использовании метода EMD невозможно заранее предсказать количество внутренних мод сигнала, поэтому при использовании EMD над отдельными семплами или над сигналом в пределах оконной функции от итерации к итерации количество внутренних мод может различаться, что наглядно показано на Рисунке 4, где представлены внутренние моды для одного и того же непрерывного сигнала в разные моменты времени. В момент времени а внутренних мод насчитывается 10, в то время как в момент времени б – 11.

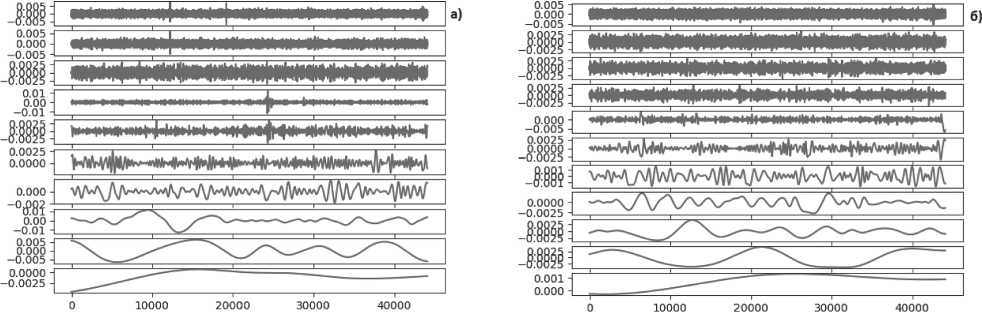
Рисунок 4. Внутренние моды одного и того же сигнала в разные моменты времени Источник: рисунок выполнен автором.

Подобные изменения количества мод могут повлиять на значения финального результата EMD PWVD, когда результаты использования PWVD на каждой внутренней моде накладываются друг на друга. Разница в количестве мод между семплами или итерациями может привести к скачкообразному изменению интенсивности сигнала на финальном результате в большую или меньшую сторону.

Одним из способов борьбы с такими артефактами может служить взятие среднего значения между значениями PWVD над каждой модой вместо прямого наложения результатов. Для определения серьезности влияния артефактов на финальный результат и эффективности борьбы с ними предложенным методом требуются дальнейшие исследования.

Заключение

EMD PWVD представляет большой интерес для преобразования непрерывных сигналов прежде всего своим высоким разрешением в частотно-временной области, унаследованным от PWVD, и отсутствием таких артефактов, как перекрестные члены. Несмотря на наличие своих собственных артефактов, EMD PWVD может быть крайне полезен при анализе непрерывных сигналов, хотя для полноценного его применения еще требуются дополнительные исследования эффективности разных алгоритмов реализации метода и методов борьбы с артефактами.

Дальнейшее совершенствование алгоритмов непрерывного EMD PWVD и способов борьбы с артефактами и расширение спектра применения данного метода для преобразования непрерывных сигналов целесообразно связывать с исследованиями в области вибродиагностики технологического оборудования, поскольку данный метод имеет большой потенциал в области преобразования и дальнейшего анализа виброакустических сигналов, что показано в работах Хонгвея Фана.