Теоретическое исследование теплообмена при движении воздуха в подземном хранилище

Введение. Для длительного хранения сельскохозяйственной продукции в хранилищах обычного типа необходимо поддержания определенного температурно-влажностного режима[1]. С разработкой теории охлаждения и кондиционирование воздуха, с изобретением холодильных установок появилось возможность решить этот вопрос. Но применения этого способа хранения требует больших затрат и это отражается на стоимости хранимой сельскохозяйственной продукции, то есть продукт становится дороже. Что и поставит задачу разрабатывать оптимальных вариантов хранилищ. К таким относятся вариант подземного хранилища, относящиеся к так называемым «безмашинным холодильникам», т.е. отсутствует холодильная установка. Охлаждения хранилища осуществляется способом аккумуляции холода в грунтовом массиве окружающий данного хранилища[7,8].

Аккумуляция холода в грунтовом массиве осуществляется двумя способами:

• 1.    Аккумуляция холода сквозным проветриванием хранилища (“пассивный” метод аккумуляции);

• 2.    Аккумуляция холода с применением грунтовых теплообменников (“активный” метод аккумуляции).

Эти две методы аккумуляции холода можно произвести в отдельности или одновременно одним или двумя центробежными вентиляторами.

Задачей об изменении параметров воздуха при движении в одиночных подземных вентиляционных каналах, т.е. в грунтовых теплообменниках, занимались П.Н.Смухин,

К.Ван-Хеерден, характеризующих вентиляционных

• Е.В. Стефанов[2-4] наиболее важный вклад в решение задач, изменение параметров воздуха при движении в одиночных подземных каналах, был сделан Е.В.Стефановым[4,5] Им было получено

аналитическое решение задачи, когда температура приточного воздуха в начальном сечении канала постоянна или меняется во времени по закону периодической функции, а проведённые экспериментальные исследования позволили получить зависимости, удобные для практической оценки изменения температуры воздуха при движении в одиночных подземных вентиляционных каналах[5,9-10] и величине относительного расстояния х ∠ 100 d от начального сечения канала до рассматриваемого.

Основная часть. При поступлении в канал воздуха с постоянной во времени температурой (стационарный процесс) эта зависимость имеет вид:

K ⋅ F

t x,τ

-

t - θ

0 гр

θ гр =eγ⋅ϑ⋅c⋅S

⋅ x

где t - температура воздуха в канале на расстоянии х (м) от начального сечения x,τ канала, 0 С;

θ гр- температура окружающего канал массива грунта, ⁰ С ;

t 0 - температура воздуха в начальном сечении канала, ⁰ С ;

• - периметр канала, м ;

• F - площадь поперечного сечения канала, м ²;

• γ , c - физические константы воздуха, принимаемые для средней температуры воздуха в канале;

• х - расстояние от начального сечения канала до рассматриваемого, м ;

• ϑ - скорость движения воздуха в канале, м/с ;

K = ψ⋅α - коэффициент нестационарного теплообмена между движущимся воздухом и массивом грунта при t 0 = const ;

а - коэффициент теплоотдачи от движущегося воздуха внутренней поверхности канала и для процесса аккумуляции холода зимой при средних значениях:

или

а = 4,16 • & 0,8 • d~ 0,2 •

а = 3,58 • & ^0,8 • d ^0,2

•

x ^	0,054	Вт
d J		20 , м • С
Г У x	- 0,054	ккал
—		20
1 d J		м • ч • С

и для процесса использование аккумулированного холода весной и летом:

а = 3,55 • & ^0,8 • d ^0,2

i// - функция граничных

Вт                       0,8 — 0,2     ккал

-------, или а = 3,05 • &  , • d ,    ----------

20                                       2   0

м • С                                        м • ч • С условий, теплофизических и временных характеристик

процесса или коэффициент

поступающего в подземный

распространения тепла для условий теплообмена воздуха, канал при tо= const, который для — < 100 характеризуется d

следующим значением:

— 0,25 „.— 0,8

/ = 4,1 • Fo ,    • Bi ’ •

у \ — 0,4

x

к d J

где d - диаметр канала, м ;

x

- относительное расстояние от начального сечения до рассматриваемого; d

а • Г(\

Bi =--- ⁰ - критерий подобия граничных условий;

Л

a • т

Fo = —— - критерий Фурье;

r а - коэффициент температуропроводности грунта, м2/ч;

r 0 - радиус канала, м ;

т - время, ч .

Проведенный анализ позволил область действия зависимостей для учёта степени охлаждения (использование аккумулированного холода) и нагревания (аккумуляции холода) приточного воздуха при движении в одиночных подземных вентиляционных каналах, что необходимо для выбора расчётных наружных температур при величине ^— <  100 . d

С целью облегчения практического использования зависимости (1) были рассмотрены возможные пределы изменения входящих величин, и, зная значения коэффициента распространения тепла в окружающем массиве / и коэффициента теплоотдачи а , основное выражение (1) было представлено в окончательной форме. Тогда для случая аккумуляции холода зимой, т.е. нагревания приточного наружного воздуха при движении в подземном канале при ^— <  100 выразится зависимостью вида: d

гр

- 1

x

-

- 0,25 0,4566 • Fo   ,

• Bi

0,8

• Re

0,2    0,65

, • Pr ,

-

гр

t ₀

= е

0,566

I x к d 7

а процесс использование аккумулированного холода весной и летом, т.е. охлаждения

x приточного наружного воздуха при движении в одиночном подземном канале при < 100 : d

t

x

— 0

-

— 0,25 0,374 • Fo   ,

• Bi

0,8

• Re

0,2

0,6 x

гр

t ₀

- 0

гр

= е

к d 7

Так как правая часть в (3) и (4) является функцией произведения критериев, то для оценки пределов её изменения необходимо оценить возможные пределы изменения данных критериев[7-10].

Выделим в (4) критериальное произведение и обозначим его через Z, тогда

₇ _ — 0,25    — 0,8     — 0,2

Z = Fo ,    • Bi ’ • Re ,

•

0,6 x

к d 7

где обозначим:

, — 0,25 ^ 1 = F 0 ^,

• Bi ^— 0,8

— 0,2 ^ 2 = Re  ’

0,6 x

•

к d 7

Z = ^ 1 • W 2.

Рассмотрим пределы изменения ^

Л 7

— 0,25

а • т

* 1 =

Г2

к 0 7

*

/      \ — 0,8

^а r0

к ^Л 7

Здесь а, Г 0 , а , Л - величины заданные, а переменным является т , т.е. время от начала процесса теплообмена воздуха с окружающим грунтом ( ч ). Коэффициент температуропроводности а и другие характеристики окружающего канал массива даны в СНиП и справочной литературе. С учётом того, что в реальных условиях почвы и грунты увлажнены, примем среднее значение а =0,0033 м²/ч. Тогда величины критериев будут находиться в пределах:

F 0 =(0 - 90);       Bi=(0 - 60);         ^ i =(0 - 10);

Пределы изменения Z равны соответственно (0 - 23). Однако, как показывают расчёты, значение Z, равное 10 и более, рассматривать не имеет смысла, так как при Z = 10 — 0, 374 •Ю величина e ,        = 0, 0237

- 0, 374 • 0,1

Нижным пределом значения Z = 0,1, так как при этом Z величина e ,     , = 0,63, что говорит об изменении температуры приточного воздуха на 0,2 ^ 0,5 0С.

Характерное время т ( ч ) заложено в критерии Fo . Все остальные величины, входящие в показатель степени числа e, представляют собой комплекс теплофизических характеристик взаимодействующих сред - грунта и воздуха. По этому для каждого конкретного случая необходимо знать e n ^Z = f ( Fo ) .

Использования возможностей математического, компьютерного моделирования является более актуальным для практического изучения данного процесса и даёт наиболее точные результаты[6].

На основе компьютерной программы - модели для случая аккумуляции холода зимой, т.е. нагревания приточного наружного воздуха получено кривые зависимости t — О

_^x „гр = f ( Fo );      t x, = f ( т ) ;

t 0 ^{— О} гр

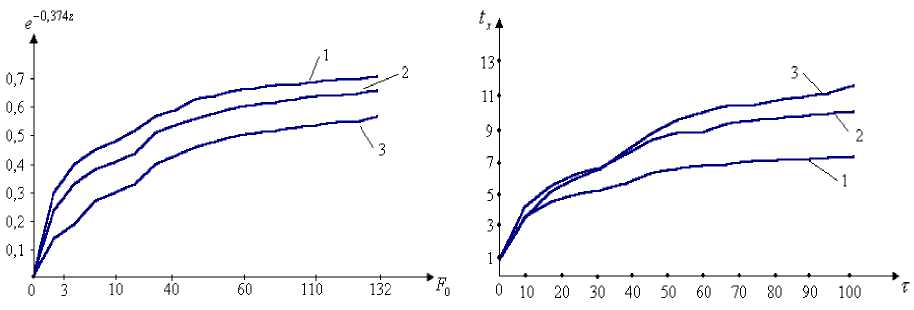
Зависимость t_x = f ( т )

О -1 гр x

Зависимость e n • z = f ( Fo )

Получены кривые зависимости

О - Г гр 0

= f (Fo ) ; t_x = f ( т ) ; с помощью

математической модели для случая использование аккумулированного холода весной и летом т.е. охлаждения приточного наружного воздуха.

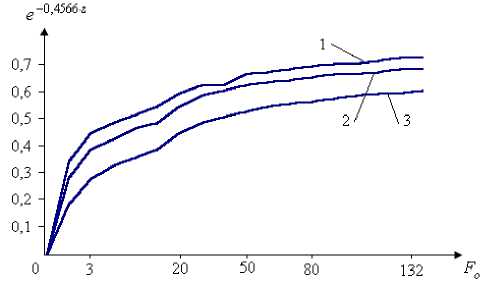
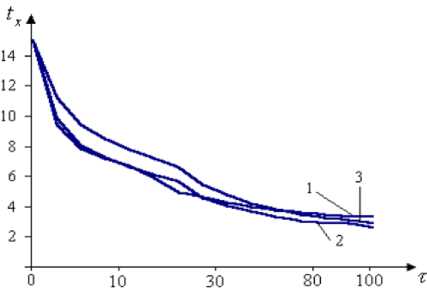
Зависимость e n ’ z = f ( Fo )                        Зависимость tx = f ( t )

где относительно оптимальным кривым является кривая 2, которая описывает более эффективное использование аккумулированного холода при температуре наружного воздуха 1 0 = 15 0 C ; и грунта 6^ = 1 0 С; х 2 = 12 м.

График даёт наглядную картинку изменения температуры приточного воздуха при движении в одиночном подземном вентиляционном канале во времени. Он может служить пособием для корректировки параметров наружного воздуха, поступающего в хранилище после прохождения по подземному вентиляционному каналу при условии, что в начальном сечени канала t 0 = const. Подобные графики могут строиться на объектах с конкретными характеристиками наружного воздуха, окружающего канал массива грунта при данных размерах подземного вентиляционного канала.

Программа модель, как научный экспериментальный исследуемый объект или средство дает конкретные результаты для различных параметров исследуемого процесса. При необходимости программу - модель можно усовершенствовать.

Изменяя входных параметров исследуемой компьютерной модели можно достичь наиболее эффективные результаты аккумуляции холода, далее с применением системы автоматического управления появится возможность экономичного использования аккумулированного холода в исследуемом объекте.

Выводы. 1. Показано, что процесс теплообмена приточного воздуха, движущегося в подземных вентиляционных каналах, имеет место на протяжении определенного периода изменения температуры наружного воздуха и эксплуатации СВ. 2. Оценены пределы изменения параметров характеризующих процесс теплообмена движущегося в подземном канале воздуха окружающим канал массивом грунта при — < 100 , to = const и зависимости d

Е.В.Стефанов[5,8] приведены к виду, удобному для расчета. 3. Составлена математическая модель (компьютерная программа) который на требуемом уровне описывает процессы подогрева и охлаждения грунтового массива и дает возможность в зависимости от входных параметров наружного воздуха получить требуемые научные результаты. 4. Составленная математическая модель можно усовершенствовать с применением новых научных разработок в области математического моделирования и теплофизики и на базе систем элементов автоматики дает возможность оптимального использования аккумулированного холода в исследуемом объекте.