Теоретическое описание процесса движения частиц зернового материала в решетном барабане

В настоящее время традиционная очистка зерна предусматривает последовательный пропуск зерна через комплекс зерноочистительных машин, на каждом из которых выделяются те или иные примеси. При этом основное зерно или семена основной культуры подвергаются многократным воздействиям рабочих органов (сепарирующих, транспортирующих и питающих устройств). Такая технология очистки зерна обусловливает повышенное дробление и травмирование зерна и семян, а также необходимость комплектования поточной линии машинами примерно одинаковой производительности. Повышение производительности зерноочистительного агрегата в данном случае будет связано с необходимостью одновременного увеличения пропускной способности всех машин, входящих в поточную линию.

Более эффективным представляется другой вариант поэтапной технологии, при котором из обработанного зернового материала по частям выделяется не примесь, а основное зерно (фракционная технология). В этом случае требуемая производительность рабочих органов на конечных этапах очистки может быть существенно ниже, чем на первых [1].

Наиболее перспективной представляется фракционная технология очистки зерна, которая уже на первом этапе обработки обеспечивает выделение 70-80% продовольственного зерна или семян, отвечающих требованиям стандарта. При этом производительность последующих сепарирующих машин можно уменьшить примерно на 70-80%. Тем самым может быть значительно повышена производительность поточной линии, так как лимитируют интенсификацию процесса очистки в большей степени именно последующие машины, в частности триеры.

В настоящее время существует проблема разработки такого зерноочистителя, который способен за одну технологическую операцию, уже на первом этапе, очистить исходный зерновой материал от всех примесей одновременно и довести большую часть основного зерна (70-80%) до базисных кондиций. В качестве такого зерноочистителя может быть использован центробежный каскадный решетный сепаратор [2]. Рассмотрим процесс движения частиц зернового материала в решетном барабане. В качестве частицы зернового материала возьмем пшеницу.

Рассматривается движение частицы пшеницы цилиндрической формы внутри решетного барабана, ось которого наклонена под углом α к горизонту.

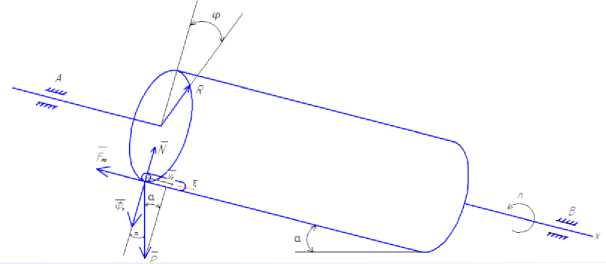
Рисунок 1 ‒ Схема механической системы барабан – цилиндр:

АВ – ось барабана; R – радиус барабана; α – угол наклона барабана, 7°; P – сила тяжести;

Ф_е – центробежная сила инерции; N – нормальная реакция; Fтр – сила трения вдоль оси ξ ;

V _c – скорость центра масс; ϕ ‒ угол наклона цилиндра; n ‒ число оборотов вращения барабана

Движение частицы зернового материала цилиндрической формы построено при следующих допущениях:

• ‒    поверхность барабана – сплошная шероховатая (рис. 1);

• ‒    ось барабана АВ под углом α к горизонту;

• ‒    R, r соответственно радиусы барабана и частицы;

• ‒    x, φ – обобщенные координаты частицы, а угловая скорость барабана ω постоянна.

Зерно пшеницы примем за цилиндр. В статье Г.И. Борисова движение частицы зернового материала рассматривалось как движение шара [3]. При движении частицы цилиндрической формы в решетном барабане частицы поворачиваются за счет сил трения длинной осью параллельно оси решетного барабана.

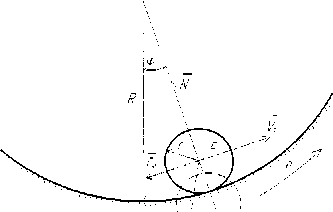
На рисунке 2 изображен срез барабана, где показаны действующие силы в поперечном плане.

to

Рисунок 2 ‒ Поперечный срез барабана:

F ф — сила трения качения вдоль оси ф ; to - угловая скорость

При этом движение частицы цилиндрической формы в обобщенных координатах описывается уравнениями Лагранжа второго рода d dt d dt

( Л

5 T   5 T

” я   ^Qф

• •    6ф

• V⁹ ф J

где X - координата и ф - угол - это обобщенные координаты; Qx и ^Q ф - обобщенные т * V_c 2   J ^ * w ?

силы; t =--- c — +------ — кинетическая энергия движения цилиндра; m — масса цилиндра;

Vc — скорость движения центра масс; J ^ - момент инерции цилиндра относительно оси сим метрии £; to^ - угловая скорость вращения относительно собственной оси симметрии ^.

Таким образом, в принятой системе координат имеем момент инерции цилиндра: т 1       2.         • .        *2         э   * 2

7 ^ = -* т * г ^; _ю^ = ф ^; vc = ^ x + ( r - r )² * ф .

Тогда кинетическая энергия системы будет равна:

m

= x

• 2                     • ²

x + (R - r)² * ф

2 m

"2"

• ² m

+ ф у * ^(R

1          2    * 2

+ m * r * ф

3 , - 2Rr + ³r²)

• ²                         • ²

= 21,5 * 10 ^{- 6} * x + 0,86 * 10 ^{- 6} *ф

Обобщенные силы Q_x , О. ф определяются из выражений для работ:

• -    вычислим элементарную работу S Ax активных сил на возможном перемещении 5х: ^ Ax = ( P * Sin a — F_Tp ) * S x ;

Fmp = P * f * Cos»,

где P = m * g , f = 0,3 - коэффициент трения цилиндра на поверхности барабана

S A_X = ( P * Sin a - P * f * Cos a ) * S x .

Тогда

„   5Ax  ( P * Sin a — P * f * Cos a ) 5 x  „                 _{x              r      x}

Q_x =---=  ---------------------— = P * ( Sin a — f * Cos a ) = m * g ( Sin a — f * Cos a ) =

= 1,18 * 10 6 .

• -    вычислим элементарную работу ^{5 А} ф активных сил на возможном перемещении Зф:

5 А ф = — * N * R * 5ф - P * Sin ф * R * 5ф ,

r где

• • ²

N = P * Cos ф + m * ф * R ;

• 6                • 2

5 А ф = — * ( P * Cos ф + m * ф * R ) * R * 5ф — P * Sin ф * R * 5ф . r

Тогда

Q ^

5 А _Ф

5ф

• 5 _ „        • 2  _ „ .  „ „

• —    * ( P * Cos ф + m * ф * R ) * R * 5ф — P * Sгn ф * R * 5ф r

б<р

= m *

5           • 2

• —    * ( g • Cos ф + ф * R ) * R — g * R * Sin ф r

= 0,57 * 10 ⁶ Cos ф + 0,01 * 10

—

• ²

ф — 85,21 * 10 ^— Sin ф ^,

где f , 5 - коэффициенты трения и качения.

Дифференцируя (2) согласно (1) получим:

d T оT     ,mx dx     ^ = 2 x(у) = x*m;

d x

d T

— = 0 , d T_ m 2      3 2

8ф    ^• = ^{2 ф} y^{( R — 2 Rr +} 2 r )

д ф

d dTТх •• • — (—) = x * m • dt • d x

d ( ^ L ) = ф * m ( r ² — 2 Rr + 3 r ²) . dt •                       2

д ф

Преобразуем уравнение (1) согласно (3), (4), (5), (6) и представим (1) в разрешенном виде относительно 2-й производной от обобщенных координат x и φ:

^{x m} = Qx

ф ^m = й ф

Подставим эти выражения (7), а также значения обобщенных сил Q x и Q φ из (3) и (4) в

уравнения Лагранжа:

•• x = g(Sina — f * Cosa)

5 ,                    _x 1 g ф = —(g * Cosф + ф * R) — — — * Sinф

Интегрирование этой нелинейной системы дифференциальных уравнений сопряжено со значительными трудностями и в замкнутой форме не осуществимо. Поэтому данную нелинейную систему уравнений интегрируем численным методом в системе MATHCAD при следующих исходных данных:

R = 0,202;     g = 9,81; а = 0,122;     f = 0,12;      5 = 0,00001;     r = 0,0015.

Для интеграции в системе MATHCAD производим замену переменных:

•                    • у 0 = x, у 1 = x, у 2 = ф, у з = ф.

Замена переменных переводит уравнение (8) в нормальную формулу:

y о = у 1

•

У 1 = 0,027

^

• y2 = y3

У д = 0,3 * Cosy ^ + 0,006 * У д ² - 48,56 * Siny^

Результаты расчетов представлены на рисунке 3.

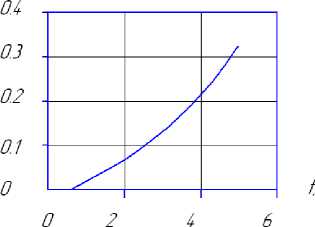
а) график изменения координаты x

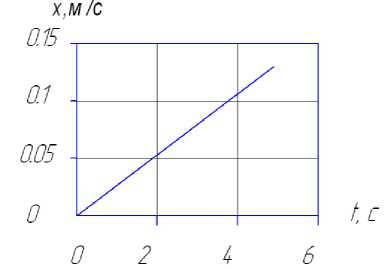
б) график изменения обобщающей скорости x

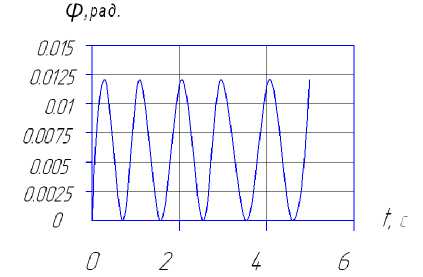
в) график изменения координаты φ

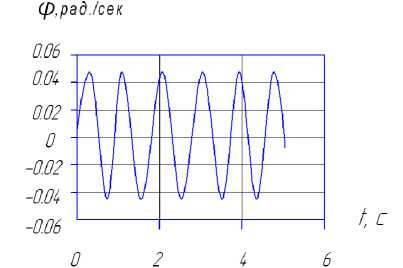
г) график изменения обобщающей угловой скорости

Ф

Рисунок 3 ‒ Графики изменения координат и скоростей

Выводы

Анализ результатов теоретического описания процесса движения частиц зернового материала в решетном барабане показал, что:

• ‒    перемещение частицы зернового материала вдоль оси x с течением времени увеличивается;

• ‒    скорость частицы зернового материала в решетном барабане со временем растет прямолинейно;

• ‒    угловая координата подъема частицы зернового материала решетного барабана имеет колебательный характер в пределах 0<φ<0,012 рад.;

•

• ‒    угловая скорость частиц зернового материала меняется в пределах -0,043 рад./c< ϕ

<0,043 рад./c.