Теория эквивалентности и ее первые результаты

В настоящее время различают четыре фундаментальных взаимодействия, проявления которых могут быть замечены и измерены в экспериментах. Два из них - так называемые сильное и слабое взаимодействия - характерны для событий, происходящих с элементарными частицами в атомном ядре, и здесь подробно рассматриваться не будут.

Электромагнитное взаимодействие обнаруживается в широком спектре масштабов, оно требует существования специальных электрических зарядов - положительных и отрицательных коэффициентов, приписываемых частицам или телам, которые характеризуют их способность участвовать в этом взаимодействии. Различные знаки соответствуют существованию сил притяжения и отталкивания. Величина силы взаимодействия точечных электрических зарядов обратно пропорциональна квадрату расстояния между ними (закон Кулона). Упорядоченное движение зарядов называется электрическим током. Если есть ток, то возникают так называемые магнитные силы, которые действуют на заряд, движущийся в его окрестности (сила Лоренца).

Наконец, гравитационное взаимодействие - самое очевидное, но и самое загадочное. Сначала Ньютон был недоволен тем, что объекты, состоящие из «косной материи», взаимодействует на расстоянии. Это не помешало ему, в конце концов, предложить теорию гравитации, которая прекрасно работает до сих пор, пока речь не заходит о тонкостях. Потом Максвелл, пытаясь приложить свой подход и к гравитации, - ведь закон взаимодействия тел там такой же, - столкнулся с тем, что притяжение тел, обладающих одноименными зарядами, означает возрастание энергии их взаимодействия при взаимном удалении. И прекратил попытки. Когда Г.Нордстрем (в 1913 году) предложил первую, скорее, формально-эвристическую, полевую теорию гравитации, то из нее следовало, что направление прецессии орбиты Меркурия должно быть противоположным наблюдаемому. Наконец, Эйнштейн постулировал принцип эквивалентности сил инерции и сил гравитации и обобщил свою (специальную) теорию относительности на ускоренные движения. Это-то и привело к созданию современной теории гравитации, также известной как общая теория относительности (ОТО) или геометродинамика. Столетие, прошедшее с момента ее создания, было наполнено разнообразными попытками обобщения самой теории и содержало фундаментальные наблюдения, существенно повлиявшие на этот процесс. А сейчас интерпретация некоторых наблюдений на основе ОТО заставляет обратиться к поиску таких загадочных сущностей, как темная материя и темная энергия. На сегодняшний день считается, что ОТО, на основе которой сформирована современная космологическая картина, представляет собой одно из высших достижений в области естествознания. (К квантовой теории, дающей потрясающие результаты, иногда предъявляется та претензия, что ее «целочисленные» законы принципиально непостижимы для человеческой интуиции, и поэтому она формальна. Эйнштейну же не нравилось присутствие в ней вероятностных законов, что приводило к неуместному предположению, что «Бог играет в кости»).

Сейчас известно несколько десятков теорий гравитации. Некоторые из них (менее десяти) сопоставимы с наблюдениями, и существует методика вычислений так называемых ППН-параметров (или пост-ньютоновских коэффициентов), с помощью которых предсказания теорий могут быть сопоставлены с экспериментальными данными. Оказывается, что данные наблюдений в Солнечной системе лучше всего согласуются с расчетами по формулам ОТО. Поэтому доверие к ОТО чрезвычайно велико. Не стоит забывать и о том, что эффект гравитационного красного смещения, предсказанный на ее основе, подтвердился с очень высокой точностью.

В настоящее время удалось свести в единую конструкцию представления о трех фундаментальных взаимодействиях - сильном, слабом и электромагнитном. Она называется стандартной моделью и служит основой физики элементарных частиц. По сравнению с временем создания ОТО нынешние представления о них заметно расширились и включают не только атомы и их ядра, не только электроны и протоны, а позже нейтроны, фотоны и мезоны, но и кварки с глюонами. Кварки обладают любопытной особенностью: они существуют только в связанном состоянии, можно сказать, что их потенциал взаимодействия не обратно, а прямо пропорционален расстоянию. Несмотря на определенные успехи в интерпретации экспериментальных данных, недостатком стандартной модели является то, что в ней слишком большое число внешних параметров, и, кроме того, она не включает в себя четвертое фундаментальное взаимодействие, т.е. гравитацию. Поэтому, так или иначе, но впереди - «новая физика», появление которой назрело. Большие надежды возлагаются на эксперименты на Большом адронном коллайдере. Однако, по состоянию на конец 2011 года существенных отклонений от стандартной модели пока не обнаружено.

1.    Классификация теорий гравитации

Оставляя в стороне возможные проблемы стандартной модели, рассмотрим более внимательно ситуацию с ОТО: откуда и почему возникли многочисленные теории гравитации, отличные от нее? В Википедии в разделе «Альтернативные теории гравитации» приведен их краткий обзор со ссылками и формулами, и желающие могут с ним познакомиться. Здесь же не ставится цель рассматривать их в деталях, нас будет интересовать классификация, тенденции, причины неувязок и пути решения возникающих проблем. Классификация этих теорий может быть произведена по двум разным направлениям.

• 1.1    Место ОТО среди других теорий

С одной стороны, классическая ОТО (геометродинамика) занимает место в ряду среди единых теорий поля, квантовой гравитации и так называемых теорий всего. Исторически, первыми после появления ОТО стали возникать именно единые теории поля, имевшие целью с единых (например, геометрических) позиций описать как гравитацию, так и электромагнетизм. Так, возникли теория Г.Вейля и теория Т. К ал у цы.

В основе подхода Вейля лежала новая геометрия (новый метрический тензор), в которой при преобразовании координат (при переходе от точки к точке) имелся дополнительный инвариант, связанный с возможностью расширения или сжатия пространства. Эту инвариантность Вейль намеревался увязать с электромагнитным полем. Она получила название калибровочной инвариантности и в дальнейшем несколько изменила смысл, а теперь известна и используется возникшая на ее основе теория калибровочных полей. Развитие геометрических идей подобного рода в применении к гравитации привело к теориям конформной гравитации, но единая теория поля пока что так и не возникла.

Калуца предположил, что четырехмерное пространство-время Минковского, т.е. то, что моделирует основные интуитивные понятия пространства и времени и служит фоном для всех событий, описываемых в теории, является лишь подпространством пятимерного пространства. Наличие правильно выбранной пятой (пространственной) координаты позволяло формально использовать новые элементы метрического тензора в качестве компонент векторов, которые и соответствовали электромагнитным величинам. Правильный же выбор состоял в том, что вдоль этого предполагаемого пятого измерения нашего мира все промежутки между точками малы настолько, что пронаблюдать и измерить их непосредственно возможности нет. Одно из измерений пространства оказывалось свернутым. В дальнейшем эта идея получила развитие: число свернутых измерений можно увеличить, если это соответствует интересам исследователя-теоретика. Проблема состоит в том, что на расстояниях, соответствующих таким свернутым измерениям известные законы классической физики, проверяемые в эксперименте, и в том числе полевая теория Максвелла, уже давно перестают работать.

Успехи квантовой электродинамики не могли не привести к попыткам проквантовать и гравитационное поле. Переносчиком гравитационного взаимодействия в таких теориях является бозон под названием гравитон. Гравитоны тоже пока не обнаружены в эксперименте, более того, в связи с геометрической природой гравитационного поля, принятой в ОТО, его квантование влечет за собой и квантование пространства-времени, что пока также затруднительно подвергнуть экспериментальной проверке. Наиболее разработанными в этом направлении являются теории петлевой гравитации.

Использованные сначала Максвеллом в электродинамике, а затем Эйнштейном при вовлечении геометрии в гравитацию абстрактные математические понятия стимулировали поиск математических основ естествознания (еще Пифагор полагал, что «все есть число») с целью построения единой теории всего. Такая теория должна начинаться с самых фундаментальных понятий и правильно описывать все явления, происходящие в разных областях и на разных масштабах физической реальности. Так, в теории струн элементарным объектом является не нуль-мерная точка, а так называемая квантовая струна, которая имеет размерность, равную единице. Она может иметь возмущения, которые можно проквантовать и интерпретировать в духе квантовой теории. Затем было естественно перейти к двумерным и так далее элементарным объектам, известным как брани. Такие теории обладают математической красотой и самосогласованностью, но имеют ли они отношение к физической реальности, сказать трудно. Пока что с их помощью не удалось описать никаких известных (или неизвестных, но измеряемых) явлений.

Таким образом, все эти обобщения, хотя и привлекают внимание теоретиков, но могут и не иметь отношения к естествознанию и в этом смысле проигрывают ОТО, которая имеет много проверяемых следствий и результатов.

С другой стороны, для того, чтобы подчеркнуть, что имеется в виду, когда говорят о классической ОТО, следует выделить несколько периодов. Первый - это классический период, известный в основном в связи с теорией гравитации Ньютона и предшествовавший возникновению ОТО. Второй -это период ее бурного развития от возникновения в 1916-м до 80-х годов прошлого века, т.е. до того, как были измерены кривые вращения спиральных галактик. И третий - продолжается до сих пор (2012), когда помимо кривых вращения были обнаружены отклонения от линейного закона Хаббла. По причинам, которые будут ясны из дальнейшего, начнем со второго периода.

/.2 Второй период - разработка u развитие

В нем можно выделить получение неочевидных результатов, следующих из уравнений самой ОТО (так называемых точных решений), и построение альтернативных теорий. Наиболее ярким примером первого явились решения А.Фридмана (и, независимо, но позже - Ж.Леметра), в которых рассматривались ситуации, связанные с нестационарной Вселенной. Полезно напомнить, что в начале 20-х годов прошлого века все, включая Фридмана и Эйнштейна, «жили» в вечной и неизменной Вселенной размером с Млечный путь и не подозревали о существовании других галактик -они считались просто туманностями, небулами. Поэтому поначалу решение Фридмана было сочтено (Эйнштейном) формальным математическим упражнением. И лишь когда через 7 лет существование галактик в результате ожесточенных споров между астрономами было уже признано, а Э.Хаббл обнаружил связанное с ними красное смещение, решение Фридмана было использовано для интерпретации этих наблюдений. Заметим, что сам Хаббл назвал Доплеровский эффект причиной наблюдаемого смещения частоты лишь во вторую очередь, а в первую - предположил наличие гравитационного красного смещения, соответствующего релятивистской модели Вселенной, предложенной Де Ситтером. Именно эта модель, в которой пространство-время имело конечный радиус, признавалась основной астрономами того времени. В связи с представлением о разбегании галактик возникла идея Большого взрыва, а Дж.Гамов предсказал реликтовое излучение, которое впоследствии было обнаружено. Однако позже само событие Большого взрыва вызвало много вопросов. В частности, на начальных этапах существования Вселенной «не было места» даже для одного кварка, а наблюдаемое распределение излучения и вещества настолько однородно, что непонятно, как такое могло быть достигнуто в результате флуктуационной неустойчивости. Возникшая теория инфляции (и ее некоторые альтернативы) всех имеющихся вопросов не сняла. Тем не менее, теории расширяющейся Вселенной, инфляции и им подобные имеют привязку к наблюдениям и сыграли важную роль в формировании космологической картины, которая существенно изменилась со времен возникновения ОТО.

Наряду с этим значительные усилия были потрачены на разработку многочисленных формальных моделей. Причиной этого являлась достигнутая максимально возможная общность подхода, который был использован при построении ОТО. Вариационный метод, примененный одновременно Д.Гильбертом и А.Эйнштейном для получения уравнений гравитационного поля, был основан на использовании одного и того же так называемого «простейшего скаляра» - геометрического объекта, не зависящего от системы координат. Но почему он должен оставаться простейшим, и каков критерий простоты? Что повлечет за собой его постепенное усложнение? Были испробованы различные предложения, однако они были либо недостаточно обоснованы, либо приводили к противоречиям с наблюдениями, либо не давали новых результатов и лишь использовали другие, зачастую более сложные процедуры. Возник целый список теорий гравитации, в который входили не только самосогласованные, полные и более-менее удовлетворительно описывающие наблюдения теории, но все те, которые в отсутствие гравитации можно было свести к СТО путем незначительных изменений. Он-то и насчитывает те несколько десятков теорий, подробно рассматривать которые необходимости нет.

/.3 Третий период 一 возникновение проблем

В 80-е годы начался новый этап развития ОТО, который на этот раз был вызван не столько возможностью, сколько объективной необходимостью: были измерены так называемые кривые вращения спиральных галактик, т.е. зависимости орбитальных скоростей звезд и межзвездного вещества от расстояния до центров их галактик. Оказалось, что данные наблюдений решительно противоречат ОТО, ее Ньютоновскому пределу и точному решению К.Шварцшильда.

Для спутника, обращающегося вокруг планеты, простая формула орбитальной скорости утверждает, что скорость спутника снижается до нуля с ростом радиуса орбиты, т.е. с удалением от планеты. Для звезды, обращающейся вокруг центра галактики, формула должна быть сложнее, что связано с характером распределения массы в галактике и положением обращающегося тела в ней. И теория Эйнштейна дает тот же результат, что и теория Ньютона: на начальном участке, соответствующем внутренней части галактики, скорости растут с ростом расстояния до центра, а после достижения определенного расстояния - скорости начинают убывать и должны стремиться к нулю. Однако наблюдения, т.е. прямые измерения этих скоростей, показывают, что с приближением к периферии видимого диска галактики скорости выходят на константы порядка 105 м/с практически для всех спиральных галактик, причем кривые вращения подходят к этим константам как сверху, так и снизу в зависимости от параметров галактики. Этот результат прост по смыслу, совсем не мал и статистически достоверен.

Первоначально это внесло оживление в среду теоретиков, и до этого пытавшихся модифицировать ОТО или построить ее альтернативы. Модификации геометрической части уравнений поля свелись к построению /(7? 丿 -теорий, т.е. к добавлению квадратичных и старших членов разложения к простейшему скаляру; к добавлению дополнительного скалярного поля; к использованию антисимметричного метрического тензора; к построению простейшего скаляра с помощью иных, чем прежде, геометрических объектов... Однако быстро стало ясно, что к требуемому результату все это не приводит. Пришлось обратить внимание на правую часть уравнений поля, отвечающую за источники гравитации, и «руками» вносить в нее такую поправку - добавочное распределение плотности вещества, - что в результате расчетные кривые вращения совпали бы с наблюдениями. Поскольку это новое вещество никак не участвует в электромагнитном взаимодействии - не излучает, как звезды, и не поглощает, как межзвездное вещество, ведь этого нет в наблюдениях,-был сделан вывод, что его частицы не являются барионами, неизвестны науке и образуют так называемую темную материю². Тем не менее, теоретическую проблему это не решило, и не только потому, что частицы темной материи не обнаружены до сих пор, но и потому, что их присутствие в теории остается подгоночным параметром. Действительно, известный закон Талли-Фишера, полученный из наблюдений, связывает светимость галактики, которая считается пропорциональной ее массе, и орбитальную скорость звезд на ее периферии. Никакой невидимой массы он не требует, а ее добавленные количества, определенные из наблюдений, должны были бы сказаться на величинах орбитальной скорости, но этого не происходит. Да и само количество массы, необходимой для подгона, в шесть раз превышает массу барионной материи в галактике, а радиус ее распределения в пять раз превышает видимый радиус спиральной галактики. Все это указывает на серьезные проблемы, справиться с которыми косметическими средствами не удается.

В этой связи возник подход МОНД (Модифицированная Ньютоновская Динамика), который поначалу не мог рассматриваться как полноценная теория, поскольку содержал радикальные, но весьма произвольные предложения. В нем предполагалось, что на галактических масштабах (при малых ускорениях) следует отказаться от привычного закона Ньютона. Причем нужно изменить либо основной закон динамики, (т.е. определение силы), либо закон всемирного тяготения так, чтобы в результате получилось соответствие наблюдениям. Были предложены формальные примеры в виде произвольно выбранных функций, обеспечивающих требуемое поведение кривых вращения.

В дальнейшем удалось переформулировать МОНД так, что она приняла релятивистский вид, но тогда оказалось, что она эквивалентна теориям с дополнительным скалярным полем, которые не свободны от противоречий. Интересным обстоятельством, связанным с теорией МОНД (и не только с ней), является тот факт, что эмпирическая константа, введенная в модифицированный закон Ньютона оказалась приблизительно равна произведению скорости света на постоянную Хаббла. Однако, является ли это случайным обстоятельством или имеет какой-либо смысл, до сих пор не было выяснено.

Эвристическое соображение, связанное с тем, что в спиральной галактике звезды распределены преимущественно в плоскости, наводит на мысль воспользоваться для описания кривых вращения решением соответствующей 2-мерной задачи. В этом случае эта кривая приобретает вид логарифмической функции, что соответствует виду некоторых (не всех) наблюдаемых кривых вращения. Но пока что не удавалось получить подобный результат «из первых принципов», т.е. в результате метризации.

В настоящее время большинство теоретиков смирилось с огромным количеством ненаблюдаемой темной материи и с логическими несоответствиями, а некоторые даже воодушевились в связи с открывающимся фронтом работ. Гравитационное сообщество сделало вид, что у классической ОТО никакой проблемы нет и переадресовало ее специалистам в области теории элементарных частиц. Из двух вариантов холодной и горячей темной материи предпочтение отдали холодной, которая известна как CDM.

Но тут подоспели новые наблюдения. Определение расстояний до ряда галактик с помощью так называемых сверхновых типа 1а, которые используются астрономами как стандартные свечи^ т.е. по светимости этих галактик, показало, что их красные смещения зависят от этих расстояний нелинейно, что в общепринятой космологической модели соответствует ускоренному расширению Вселенной. Это вновь привлекло внимание к ОТО. Для ускоренного расширения нужна энергия -конечно, тоже темная, так как никаких подходящих взаимодействий отталкивания на таком масштабе неизвестно. Вспомнили о космологическом члене, или Л-члеие, который использовался Эйнштейном в уравнении поля при постановке космологических задач для стационарной модели Вселенной, но был им отброшен, поскольку приводил к неустойчивым решениям. Стали говорить о квинтэссенции - пятой сущности с пятым же типом фундаментального взаимодействия. Установили связь Л-члеиа с радиусом пространства Де Ситтера, в котором пустое пространство имеет ненулевую кривизну, что довольно странно, т.к. основная посылка ОТО состоит в том, что единственным источником кривизны пространства-времени является распределение тяготеющих масс. В итоге — последним словом науки о гравитации в настоящее время является модель ACDM, представляющая собой стандартную модель космологии Большого взрыва, следующую из решения Фридмана для классической ОТО. Оценки, сделанные с учетом эквивалентности массы и энергии, показывают, что теперь на долю как светящейся, так и несветящейся, но наблюдаемой материи, которые присутствовали в теории изначально, в сумме приходится не более 4% материального содержания Вселенной. Остальные 96% - это темные понятия. Разрыв гравитации с остальными тремя фундаментальными взаимодействиями по-прежнему представляется трудно преодолимым. Поэтому некоторым исследователям трудно считать эту ситуацию удовлетворительной, а утверждения, лежащие в основе ОТО, трудно считать несомненными. При этом, строго говоря, следует различать проблему, связанную с кривыми вращения, т.е. с темной материей, и проблему, связанную с нарушением закона Хаббла, т.е. с темной энергией. Первая относится к классической ОТО, а вторая - уже к решению Фридмана, на основе которого возникла новая космологическая картина. Для того, чтобы попытаться выяснить, почему теория, отлично работающая на планетарном масштабе, приводит к сомнительным результатам на галактическом масштабе и выше, следует обратиться к первому - доэйнштейновскому - периоду в развитии теории гравитации. Тогда, возможно, эти причины станут более ясными и можно предложить направление поиска новой теории.

/・4 Первый период - анализ основ

Первый период известен в основном, конечно, классической теорией гравитации Ньютона3. Она была основана на точных результатах астрономических наблюдениях движения планет в Солнеч- ной системе. Закон этого движения (позднее - после «истории с яблоком» - закон всемирного тяготения, т.е. гравитации) был получен из третьего закона Кеплера4, но и первый закон Кеплера сыграл свою роль: Ньютон подчеркивал эллиптический характер орбит и вообще значение конических сечений. Однажды он упомянул и про то, что линейная зависимость силы от расстояния тоже приводит к этому классу траекторий, но отверг ее, как несостоятельную и более не упоминал. Его современник Р.Гук делал это более настойчиво и полагал, что Солнце находится в центре, а не в фокусе эллипса, а П-С.Лаплас - несколько позже - просто утверждал, что в закон гравитации входят оба члена, и на этой основе установил, что орбита планеты должна иметь прецессию и напоминать розетку. Напомним, что именно измеренная впоследствии прецессия орбиты Меркурия, приводящая к подобной розетке, стала тестом для полевых теорий гравитации. И, кстати, если подумать о траектории, по которой полетело бы падающее (под углом) яблоко, способное пронизывать земной шар, то это был бы эллипс именно с центром, - а не с фокусом! - в центре Земли. Это несложно понять, вспоминая школьную задачу о напряженности поля однородно заряженного шара: внутри него поле линейно растет с расстоянием до центра, снаружи - убывает по закону обратных квадратов, а на поверхности шара обе величины совпадают. Можно говорить о сшивании решений внешней и внутренней задач. Поле, прямо пропорциональное расстоянию до центра, носит характер квазиупругой силы и приводит к эллиптической траектории с центром в центре притяжения. След этой задачи виден и в росте кривых вращения на начальном участке зависимости орбитальной скорости от расстояния до центра галактики.

Иногда подчеркивают, что существенную роль в дальнейшем развитии теории гравитации сыграл принцип Э.Маха, который оказался своеобразным мостом между философской основой теории Ньютона и философской основой теории Эйнштейна. Действительно, Ньютон полагал, что выделенная система отсчёта связана с абсолютным пространством и временем; Мах считал, что выделенная система отсчёта связана с неподвижными звездами, т.е. с распределением материи во Вселенной; а Эйнштейн постулировал, что выделенной системы отсчёта не существует, и всю теорию построил так, чтобы при переходе от одной системы отсчета к другой все физические процессы протекали бы одинаково и давали один и тот же результат. Эти обстоятельства, несомненно, важны, однако, представляется, что с одной стороны, проблема лежит глубже, а с другой - были упущены некоторые важные детали.

В основе ОТО лежат два фундаментальных принципа, первый из которых - принцип относительности -дал название всей теории. Принцип относительности Галилея утверждает, что «для предметов, захваченных равномерным движением, это последнее как бы не существует и проявляет своё действие только на вещах, не принимающих в нём участия». Эта формулировка возникла в процессе борьбы за утверждение идей Коперника и самого Галилея о годовом и суточном вращении (движении) Земли. Причина появления в названии слова «относительность» состоит в том, что при относительном движении двух тел не всегда возможно определить, которое из них движется, а которое покоится, т.е. что движется относительно чего, однозначно сказать невозможно. Несколько позже Ньютон уточнил эту мысль: «все физические [механические] процессы в инерциальных системах отсчета протекают одинаково». Если у Галилея речь шла о некотором «равномерном движении», то Ньютон использовал понятие «инерциальной системы отсчета». Под ней он понимал такую, в которой все свободные тела, (то есть те, на которые не действуют внешние силы или действие этих сил скомпенсировано), двигаются равномерно и прямолинейно или покоятся. Это несущественное для механических экспериментов «равномерное и прямолинейное движение» объекта наблюдения относительно наблюдателя было «зашито» непосредственно в уравнение динамики Ньютона, которое он ввел, воспользовавшись развитым им языком исчисления бесконечно малых. Именно в этом виде принцип относительности был использован и расширен Эйнштейном, включившим в него и электродинамические процессы, в этом виде знаем мы его и сейчас. Иногда говорят, что инерциальное движение соответствует однородности и изотропности пространства. Соответственно, всякая система отсчета, движущаяся с ускорением относительно инерциальной системы, является неинерциальной.

Уточнение, связанное с привлечением математики, придало принципу относительности дополнительный смысл. Теперь он становится не столько естественнонаучным обобщением наблюдаемых фактов, как у Галилея, сколько метафизическим, философским и непроверяемым постулатом. Действительно, следующим фундаментальным шагом становится введение Ньютоном принципа эквивалентности, когда закон динамики используется для определения силы гравитации в Солнечной системе и объяснения постоянства ускорения свободного падения для разных тел, наблюдаемого на поверхности Земли. Но тогда, если имеет место и закон всемирного тяготения, то существование во Вселенной более чем одного тела, обладающего массой, считая наблюдателя или тело отсчета, в принципе исключает существование систем, движущихся без ускорения. Поэтому философский (математический) принцип относительности не может быть проверен и становится вопросом веры, постулатом, необходимым для обоснования приближенного подхода. Считается, что физические инерциальные системы, которые мало отличаются от «истинных», т.е. от математических, существуют, хотя измерить величину этого малого отличия возможно не всегда. Таким образом, получается, что физика в большой степени опирается на подразумеваемое общепринятое соглашение о том, что законы природы тождественны соответствующим дифференциальным уравнениям⁵. Эти соглашения привели сначала Ньютона, а затем Эйнштейна к теориям гравитации, успех которых в интерпретации известных наблюдений и предсказании новых оправдал этот шаг. Поэтому то, что инерциальные системы отсчета представляют собой математическую абстракцию, недоступную для наблюдений, оговаривают лишь изредка. В этом смысле принцип эквивалентности, который состоит в том, что никаким физическим экспериментом невозможно отличить действие сил инерции от гравитационных сил в данной точке, отличается от принципа относительности и может быть проверен⁶.

Использование этих двух принципов именно в таком порядке - сначала принципа относительности для построения СТО, потом принципа эквивалентности для построения ОТО - привело к построению той классической ОТО, у которой и возникли проблемы на третьем этапе ее развития.

Представим себе, однако, такую ситуацию: будем наблюдать движения молекул неидеального газа, находясь на одной из таких молекул. Будем условно считать взаимодействие между ними гравитационным, принцип эквивалентности выполненным, но закон гравитации - неизвестным. Для описания движения наблюдаемой молекулы следует ввести какую-нибудь систему координат, и наиболее естественный выбор - это система, связанная с наблюдателем. Но что можно сказать о движении самого наблюдателя? Его движение не задано, но точно так же определяется взаимодействием с другими молекулами, как и движение объекта наблюдения. Что же из наблюдаемого движения (произвольного вида) связано с взаимодействием наблюдаемой молекулы с ее соседями, а что - с движением наблюдателя⁷ , т.е. с взаимодействием молекулы, на которой он находится, с ее окружением? Как судить о характере движения тел, - а, значит, и о характере (гравитационного) потенциала взаимодействия между ними - иначе, чем опираясь на наблюдения движений самих этих тел? Как проверить полученные выводы? Кроме того, есть ли основания допустить близость хоть какого-нибудь из этих движений к равномерному и прямолинейному и как проверить такое допущение?

Исключая из рассмотрения привилегированное тело отсчета (не только абсолютный эфир, но и, например, массивное центральное тело, в поле которого движется пробное тело, масса которого мало влияет на движение центрального тела), мы утрачиваем не только право с определенностью говорить о любом заданном движении наблюдателя, но даже судить об инерциальности или неинерциальности системы отсчета, в которой он находится8. Понятие равномерного прямолинейного движения более не может быть естественно применено к описанию наблюдаемого движения. Оно превращается в полностью умозрительное и возвращается в лоно математики. Таким же образом, судить о свойствах однородности и изотропности реального (наблюдаемого) физического пространства больше возможности нет.

В ОТО принималось, что метрика в присутствии гравитации начинает зависеть от координат точки, и пространство-время приобретало кривизну, на нем возникал рельеф. Теперь мы видим, что этого недостаточно, и каждой точке следует сопоставить не только локальный скалярный потенциал, но и (пока еще не определенный) вектор, отражающий состояние движения имеющихся тел. Формальные теории гравитации, в которых метрика содержит вектор9, встречаются, но смысл такой добавки не всегда обсуждается в достаточной степени10.

Возвращаясь к принципу Маха, можно заметить, что во всех трех утверждениях, приведенных выше, главную роль играла выделенная система отсчета. У Ньютона она была математической абстракцией, у Маха - физически недостижимым, но наблюдаемым объектом, у Эйнштейна утверждалось, что выделенная система отсчета отсутствует, но другие системы - заданные - существовали и, таким образом, позволяли установить закон взаимодействия между телами, который не менял своего вида при переходах из системы в систему. Однако теперь оказывается, что система отсчета как таковая, т.е. такая о свойствах движения которой мы ничего не знаем, не помогает узнать ничего и о движении наблюдаемого тела в связи только с его взаимодействием, с его окружением. Это означает, что в подобной ситуации принцип относительности оказывается в глобальном смысле бессодержательным, т.к. не удается установить законы, которые могли бы меняться или не меняться при переходе из ИСО в ИСО. А в локальном смысле принцип относительности нуждается в непосредственной формулировке условий, при которых можно говорить о его выполнении. Иными словами, он оказывается применимым лишь в определенных частных (предельных) случаях - в них-то и будет работать ОТО. Эти утверждения не имеют отношения к тому, что обсуждается, когда в ОТО говорят о ситуации на бесконечности, где пространство считается плоским.

Таким образом, из приведенных рассуждений следует, что обобщение результатов СТО на ускоренно движущиеся системы с учетом принципа эквивалентности, ведущее к ОТО, содержало произвол, связанный с неявным представлением о том, что характер движения наблюдателя полагался известным. На галактических (космологических) масштабах, где движущиеся тела становятся сравнимыми, этот произвол может привести к проблемам в интерпретации наблюдений, что и произошло в последние десятилетия. Это означает, что построение непротиворечивой теории гравитации следует начинать с принципа эквивалентности, опираться на наблюдения, а уже в рамках построенной теории при необходимости рассмотреть предельные случаи, соответствующие ОТО и СТО.

2.    Обобщение принципа эквивалентности

Немедленным следствием приведенных рассуждений является то, что для построения теории гравитации на галактических масштабах закон динамики Ньютона в традиционной форме более не может применяться. Ясно, что новый его вид должен учитывать (в общем случае ускоренное) движение наблюдателя, причем факторы, определяющее это движение, должны учитываться в законе динамики самосогласованно. Последнее достигается за счет использования принципа эквивалентности, который при этом должен быть обобщен. Таким образом, различие между законами динамики и гравитации окончательно исчезнет.

Обобщение принципа эквивалентности следует произвести по двум направлениям. Первое - физическое -связано с учетом того, что поскольку силы инерции имеют составляющие, зависящие от скорости тела, то и силы гравитации должны такие составляющие иметь11. Второе направление связано с возможностями измерений, которые теперь выполняются заведомо удаленно, т.е. включают распространение электромагнитных сигналов, и новая теория с неизбежностью должна быть релятивистской с самого начала. Удаленность потребует введения параметра, имеющего размерность длины, и поэтому смысл понятия локальность в принципе эквивалентности также должен измениться. С математической точки зрения это будет означать, что все возникающие задачи должны быть предварительно квалифицированы либо как внешние, либо как внутренние, а на границе должно выполняться условие сшивания решений.

Выпишем обычное уравнение движения в неинерциальной системе отсчета, движение которой считается заданным. Оно имеет вид dv m— dt

dU = 工

—-^ — mW + m[r, С] + 2m[v, Q] + m[C, [r, C]]

(2.1)

Слева стоит произведение массы наблюдаемого тела на его ускорение, а справа - градиент некоторого силового потенциала и сумма сил инерции, определяемых движением системы отсчета. Как и откуда величины такого рода могут быть измерены в ситуации, упомянутой выше, когда о движении системы отсчета ничего не известно? Принцип эквивалентности требует, чтобы величина гравитационной массы (заряда), входящего в первое слагаемое в правой части, была равна той же т, что находится во всех остальных членах уравнения. Поэтому, измеряя ускорение наблюдаемого объекта относительно некоторой системы отсчета и умножая его на его массу, мы по определению получим выражение для силы, действующей на него. Но как справиться с проблемой, возникающей из-за отсутствия системы отсчета, известный закон движения которой дал бы остальные выражения в правой части? Воспользуемся полевым подходом Дж. Максвелла.

3.    Тождества Максвелла и метрическая теория

Обсуждая смысл теории Максвелла в применении к электродинамике, можно заметить, что Максвелл обнаружил, что физика электрических и магнитных явлений неожиданным образом следует из совершенно абстрактной математики. Надо взять математический объект («антисимметричный тензор второго ранга»), для которого справедливо некоторое геометрическое тождество. Расписанное для каждой компоненты, это тождество дает 6 соотношений. Если обозначить каждую из компонент буквами, соответствующими обычным обозначениям для напряженностей электрического и магнитного полей, то появится первая система (однородных) «уравнений Максвелла», не узнать которые невозможно. Несколько изменив выбранный тензор с учетом геометрии, избранной для использования, можно с помощью такой же манипуляции с обозначениями получить и вторую пару уравнений Максвелла - уже с «зарядами» и «токами». При этом никакой физики в этих уравнениях изначально не содержится, буквами можно обозначать, что угодно. Так что надо специально постановить, что введенные обозначения соответствуют измеряемым величинам электрического заряда, электрического тока и соответствующих напряженностей, т.е. измеряемым силам. И тогда следствиями этих общематематических уравнений будут те самые законы физики, которые были известны и до Максвелла, который их «обобщил». В том числе появятся выражения для силы Кулона (электрической силы) и силы Лоренца (магнитной силы).

С помощью этого подхода можно показать, что при выполнении измерений из той или иной (инерциальной) системы отсчета, движущейся с той или иной скоростью относительно движущихся зарядов, магнитные силы будут становиться электрическими и наоборот. Говорят, что в этом проявляется относительность электрических и магнитных полей, т.е. они являются сторонами одной сущности - электромагнитного поля.

Характер зависимости электрической силы Кулона от расстояния между зарядами ничем, кроме обозначений, не отличается от гравитационной силы Ньютона, определенной им в околоземных условиях с помощью закона динамики. Поэтому буквы могут обозначать и гравитационный заряд (гравитационную массу), гравитационный ток (ток массы) и соответствующие напряженности и потенциалы. Эта идея, естественно, пришла в голову и Максвеллу. Рассуждавший в терминах классической физики, он быстро столкнулся с той проблемой, что сам факт притяжения тел, обладающих массой, (т.е. одноименных зарядов), означает возрастание энергии взаимодействия тел при их взаимном удалении, и отказался от ее дальнейшего обдумывания12. Если же попытаться строить метрическую теорию, как впоследствии поступил Эйнштейн, то действовать нужно иначе .

Заметим, что структура выражения для силы Лоренца в электромагнетизме напоминает выражение для силы Кориолиса в механике (четвертое слагаемое справа в формуле (2.1)). Тогда естественно предположить, что вектор (в метрике), о котором шла речь в предыдущем разделе, соответствует сумме полей, создаваемых токами массы, т.е. всеми движущимися массивными телами. В электромагнетизме последняя величина вычисляется с помощью интегрирования, зависит от точки наблюдения и системы отсчета (относительность электрического и магнитного полей!) и имеет знакомый вид. Для определения скоростей частиц следует воспользоваться вычислением производных от координат по естественному параметру, как это обычно делается.

Для построения метрической теории, т.е. такой, в которой физические взаимодействия приводят к движению по траектории, которую можно описать, задавая геометрическую форму некоторой поверхности, существенно то, что наличие вектора в каждой точке пространства делает это пространство анизотропным, т.е. его свойства по разным направлениям будут различаться. Это имеет глубокий смысл. Интуитивные понятия пространства и времени являются базовыми в восприятии реального мира. Для их описания в настоящее время используется модель изотропного пространства-времени, введенная Минковским, наделенная Римановой геометрией. Теперь этой модели и этой геометрии будет недостаточно. Привычная Лоренц-инвариантность теперь будет представлять собой исключение, соответствующее частному случаю, когда есть основания допустить, что принцип относительности выполняется, а группа Пуанкаре более не будет являться основной группой преобразований координат. Таким образом, использование принципа эквивалентности в качестве исходного пункта потребует значительного пересмотра существующих фундаментальных представлений. Это вызывает законные опасения. Так было и сто лет назад, когда Пуанкаре отказался рассматривать переход к неевклидовой геометрии четырехмерного пространства ввиду трудоемкости предстоящего в этом случае пересмотра физики. Но впоследствии Минковский настоял на этом, опираясь на результаты, полученные в результате применения подхода Эйнштейна для описания электродинамики движущихся тел и интерпретации опытов Майкельсона-Морли:

«Взгляды на пространство и время, которые л собираюсь изложить, основаны на результатах экспериментальной физики, и в этом их сила. Взгляды эти радикальны. Отныне пространство само по себе и время само по себе уходят в мир теней, и сохраняет реальность лишь их своеобразный союз.. .》

По-видимому, в связи с новыми наблюдательными данными нечто подобное ожидает нас и теперь.

4.    Построение анизотропной геометродинамики (теории эквивалентности)

Итак, помимо привычных модификаций теории, связанных с уравнениями, теперь, как и сто лет назад, предлагается сначала обратиться к вопросу о том, как следует моделировать базовые интуитивные представления, чтобы, исходя из наблюдений и соображений, приведенных выше, сделать следующее:

• •    ка.ждой точке реального ( 1 ) іг:иг-ісч?кого пространства сопоставить некоторый вектор ：

• •    естествеппым образом ввести ( 1 ) упдамепталыіып параметр с рагшериостьто длины ：

• •    in? утратить ( 1 ) ігзііч ( ?скііп смысл при іісполь ： зоваіііш мат ( ?матпч ( ?ского (формализма.

4・/ Фазовое пространство-время

Идея, положенная в основу теории эквивалентности [S.Siparov. Introduction to the Anisotropic Geometrodynamics. World Scientific, 2011], состоит в том, что такой моделью является фазовое пространств о-время. Оно является аналогом широко используемого в физике фазового пространства. Обычное фазовое пространство имеет 6 измерений: 3 координаты и 3 соответствующих проекции скорости движущейся частицы. Несмотря на несколько формальный характер, физический смысл его измерений вполне прозрачен, фазовые траектории (графики, где на одной оси отложена координата, а на другой - скорость) имеют наглядный характер и позволяют судить о динамике систем. Классическая механика в пространстве состояний {положение, скорость} является развитой и перспективной наукой.

Построение фазового пространства-времени происходит путем дифференцирования координат тела, двигающегося по траектории, по естественному параметру, связанному с этой траекторией, i т.е. . yi = dds . % = о.... J. Для пространства-времетш таким ес工 ес工 венннм параметром можно считать произведение ds = cdt, где с - фундаментальный параметр, имеющий размерность скорости. Эти четыре производные и становятся дополнительными четырьмя измерениями фазового пространства-времени, которое, таким образом, имеет 8 измерений. Обратим внимание на два важных обстоятельства:

• •    точно так 本已 как Минковскому потребовался переводиоп KO< )( j )( j ) iiTiiienT с. пметошпп размерность скорости, для того, чтобы все координаты пространства-времени имели одну и ту же единицу измерения, теперь с этой же целью требуется еще один переводной коэффициент, имеющий размерность длины: на него должны быть умножены безразмерные величины yi, получившиеся после дифференцирования;

• •    первая (нулевая) ш введенных дополнительных координат окггзывается постоянной в ( ?личиной.

• 4.2 Основные уравнения и понятия

Последнее означает, что и второе требование оказывается выполненным - у теории есть фундаментальный параметр с размерностью длины, при этом его значение соответствует фиксированной величине одной из координат фазового пространства-времени. Так что все события будут разворачиваться на 7-мерном подпространстве фазового пространства-времени. Как уже было сказано, в каждой его точке имеется вектор, равный сумме полей, создаваемых всеми токами массы. Его наличие делает фазовое пространство-время анизотропным пространством.

Основными уравнениями теории являются уравнение геодезической и уравнение поля. Геодезической в геометрии называется линия экстремального расстояния между двумя точками. Если справедлив принцип эквивалентности, то ее уравнение соответствует закону движения и одновременно приводит к выражению для гравитационной силы. Естественно, уравнение геодезической должно теперь оказаться несколько иным, чем в ОТО, так как в нем должны присутствовать дополнительные члены, связанные со скоростями (точнее, с производными yi). Это уравнение получают путем варьирования выражения для длины дуги, которая теперь вычисляется с учетом анизотропии метрики, т.е. с учетом избранной геометрии. Последняя уже не может быть Римановой, поскольку метрика содержит производные координат. Общим случаем является так называемая обобщенная геометрия Лагранжа (частным случаем - геометрия Финслера). При этом следует подчеркнуть, что анализ ситуации, проведенный выше в разделе 4, требует не угадывания явного вида метрики с целью получения желательного или красивого результата, но лишь последовательных и самосогласованных рассуждений.

Это означает, что для дальнейшего продвижения следует поступить так же, как Эйнштейн в своей основополагающей работе: ограничиться случаем слабого поля (линейным приближением), то есть рассмотреть незначительно искривленное (теперь еще и незначительно анизотропное) пространство. Это удобно еще и потому, что, как можно показать, в таком приближении уравнение поля не изменится, и только входящие в него выражения для символов Кристоффеля (коэффициентов связности) будут зависеть еще и от yi. Получив выражение для обобщенной геодезической14, можно использовать его одновременно в качестве уравнения динамики и как основу для нового закона гравитации.

В простейшем случае выражение для гравитационной силы будет состоять из двух слагаемых15. Одно из них при отсутствии анизотропии (при отказе от учета токов массы) совпадает с выражением, имеющимся в ОТО, и ведет к знакомому Ньютоновскому потенциалу. А второе слагаемое содержит скорость тела и вектор, определяемый токами массы. Новым обстоятельством является возможность появления отрицательной поправки к обычному выражению для гравитационной силы вплоть до преобладания (наблюдаемых) сил отталкивания над силами притяжения. Но это не должно удивлять, т.к. связано с тем, что в основе теории лежит принцип эквивалентности, и гравитационные силы эквивалентны силам инерции, а последние включают в себя, например, центробежные силы. Возможно также и появление дополнительных (наблюдаемых) сил притяжения, связанных с движением. Но и это находится в соответствии с общими идеями СТО и ОТО, согласно которым кинетическая энергия внутреннего движения системы тел должна давать вклад в массу этой системы. Наблюдаемость сил означает, конечно, возможность измерения соответствующих ускорений.

Соответствующий гравитационный потенциал также будет иметь два слагаемых. Важно отметить, что второе из них связано с тангенциальным движением пробного тела относительно наблюдателя:

• • как и в ОТО іісполь：зоваіше грав пт анионного потенциала приводит к замедлспито времени и соответственно, к выражению для гравитационного красного смещения. Из-за наличия нового слагаемого теперь оно сразу оказывается линейно зависящим от расстояния до наблюдателя, что соответствует закону Хаббла.

5.    Примеры использования ТЭ для расчетов на галактических масштабах

Новый вклад напоминает результат действия сил инерции во вращающейся системе отсчета, но не является им. В отличие от последнего, на бесконечности соответствующее слагаемое в гравитационной силе обращается в ноль из-за интегрирования по углам выражения, связанного с токами массы.

Существование дополнительных слагаемых в полученных выражениях означает, что в качестве модели элементарного источника гравитации больше нельзя использовать уединенную массивную точку. Для такого источника вклад второго слагаемого, связанного с движением, будет отсутствовать, т.е. произойдет переход к ситуации Ньютона-Эйнштейна, для которой будут справедливы результаты ОТО. Поэтому элементарным источником следует считать систему «центр плюс ток» (ЦПТ), т.е. (гравитационный) заряд, окруженный круговым контуром с током (массы). Тогда проявят себя вклады обоих слагаемых. С математической точки зрения это означает, что у поля имеется как потенциальное слагаемое, так и соленоидальное. Именно такая модель используется в следующем разделе для расчетов на галактических масштабах. Конкретный вид и вклад второго слагаемого зависят от того, какая именно система движущихся масс (например, какой тип галактики) рассматривается.

Для таких галактик, как М-104 (Сомбреро) или NGC-7742 (рис. 1а,Ь), наделенных кольцом, модель ЦПТ может быть применена непосредственно. Для спиральных галактик с более выраженными рукавами (рис.1с) несложно ввести и вычислить эффективные значения ее параметров по данным наблюдений. Можно определить условия - расстояние от центра и орбитальную скорость, -при которых оба члена в выражении для силы начинают играть сопоставимую роль. Оказывается, что при соответствующем (априорном, а не подгоночном) выборе констант теории (см. ниже) они дают значения, измеряемые в астрономических наблюдениях на галактических масштабах. Поэтому расхождение соответствующих предсказаний теорий Ньютона-Эйнштейна, сделанных на основе точечной модели источника, с результатами измерений кривых вращения для спиральных галактик не является удивительным.

При решении задачи об описании кривой вращения для гравитационной системы ЦПТ в ее плоскости можно при вычислениях использовать выражения, известные из электродинамики, которые имеют тот же вид в силу упоминавшегося происхождения уравнений Максвелла. Получаемый ответ дает два значения орбитальной скорости: одно равно нулю, что соответствует Ньютоновскому решению, а второе представляет собой константу, определяемую параметрами распределения масс в галактике.

Если при оценке величины этой константы воспользоваться предположением о постоянном отношении массы к светимости, (это принимается как одно из основных соотношений при определении расстояний в астрономии), то мы автоматически получим закон Талли-Фишера, упоминавшийся в разделе 2.3.

Рис. 1. Спиральные галактики: а - М-104, b - NGC-7742, с - NGC-1300 (Изображения получены с помощью телескопа «Хаббл»)

Таким образом, то, что в ОТО представляет собой проблему рассогласования с наблюдениями, требующую дополнительного введения большого количества темной материи^ в ТЭ является не проблемой, а естественным результатом, следующим из использованных предпосылок.

Это обстоятельство побуждает исследовать подробнее другие аспекты, которые можно сопоставить как с известной теорией, так и с наблюдениями. В частности, наряду с гравитационным красным смещением, которое уже упоминалось, можно обратить внимание и на два другие классические теста ОТО - прецессию орбиты (здесь: орбиты звезды вокруг центра спиральной галактики) и отклонение луча света. То, что прецессия будет иметь место, предсказуемо, поскольку к ней ведет любое отклонение потенциала от Ньютоновского. А отклонение световых лучей, испущенных источником, находящимся за спиральной галактикой (например, квазаром), рассчитанное по формулам ТЭ, будет зависеть от ориентации плоскости галактики относительно наблюдателя. Это последнее может иметь отношение к ситуации, когда наблюдаемое отклонение лучей в гравитационных линзах в разы превосходит то, которое дает расчет по формулам ОТО. В этом случае также ссылаются на наличие темной материи и оценивают ее количество по расхождению наблюдаемого и расчетного отклонений.

Расчет движения звезды в спиральной галактике с эффективным радиусом тока массы, отмеченным дугой окружности на рис.2, для зависимости декартовых координат у(х) дает траектории, представленные на рисунке. В зависимости от параметров задачи и начальных данных можно обнаружить

• •    npeneccnio оу ) биты звезды (а),

• •    инфинитное движение (1. ) ).

Траектория, показанная справа, имеет отношение к еще одной известной наблюдательной проблеме. Шаровые скопления, которых в нашей галактике известно около полутора сотен, чаще обнаруживаются в окрестности центра галактики, а не на периферии, где они должны были бы проводить большую часть времени своего существования в соответствии с представлениями Кеплера об эллиптических орбитах - основе гравитации Ньютона. Но из ТЭ следует, что если плоскость траектории скопления близка к плоскости галактики, то влиянием массового тока, связанного с орбитальным движением звезд вокруг центра галактики, пренебречь нельзя, и оно может приводить к ситуации, представленной на рис. 2 Ь, т.е. удерживать скопление вблизи центра. При этом движение в ортогональной плоскости будет Кеплеровским, так как второе слагаемое используемого выражения для гравитационной силы в этом случае вклада давать не будет.

Эти результаты ТЭ соответствуют первому классическому тесту ОТО в применении к галактическим масштабам и проясняют ситуацию с поведением шаровых скоплений в нашей галактике.

Иллюстрация расчета отклонения луча при прохождении справа налево вблизи обычного центра (слева) и вблизи системы ЦПТ с нужной ориентацией приведена на рис.З.

Оказывается, что:

• •    отклонение луча, имеет место и может быть у ) а.ссчитало,

• •    во втором случае (при учете тока, массы) отклопение луча. существенно больше, что может объяснить количественные расхождения при непосредственном наблюдении гравитационных линз.

  

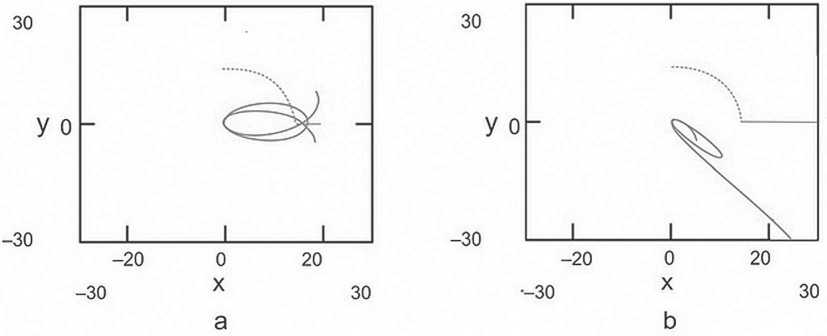
  Рис. 2. Траектории тел в координатах (х,у). Дуга окружности соответствует положению эффективного кругового тока массы; а - витки розетки обходятся против часовой стрелки; b - пробное тело, пребывавшее в окрестности центра, покидает ее и уходит на бесконечность)

  
  
  

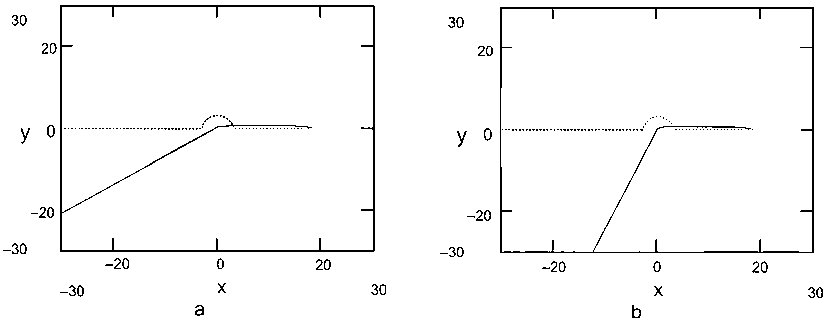
  Рис. 3. Траектории тел в координатах

  положению эффективного кругового тока массы, который в случае За не учитывается)

  (х,у). Дуга окружности соответствует

  
  

В ОТО гравитационная линза обладает центральной симметрией и имеет параметр, называемый радиусом Хвольсона-Эйнштейна16. В терминах ТЭ профильная ориентация линзы по отношению к удаленному источнику (квазару) такую симметрию теряет, и можно получить формулу, в которой вместо одного значения радиуса будет два17. Применяя полученные формулы к такому известному объекту, как Крест Эйнштейна, что оправдано в связи с учетом вида и ориентации самой галактики-линзы (рис.4, центр), можно убедиться, что они не противоречат наблюдениям. Таким образом, можно вновь заметить, что:

• •    наблюдения отклонений в гравитатцюппой линзе, которые при пх пнтерпретатиш с помотпы 。

ОТО требуют введения темной материи, при использовании ТЭ в ней не нуждаются.

При этом и в приведенном примере ТЭ дает результаты, согласующиеся с наблюдениями.

Помимо этого численное моделирование системы ЦПТ для различных условий и начальных данных, выполняемое в рамках подхода ТЭ, позволяет обнаружить немало интересных паттернов, весьма сходных с наблюдениями. Это позволяет выдвинуть новые гипотезы образования рукавов и баров (перекладин) у спиральных галактик (последние имеются примерно у двух третей из них). Заметим, что происхождение баров до сих пор оставалось неясным.

На рис.5а приведен результат расчета взрыва центрального тела в модели к выбросу двух равных масс в противоположных направлениях в плоскости этих масс весьма напоминают известные наблюдения, получаемые с помощью (ср. рис.5а и 5Ь).

ЦПТ, приводящего витка. Траектории телескопа 《 Хаббл»

¹⁶ Радиус Хвольсона-Эйнштейна рассчитывается по формуле: £° = J 2rs D d D ds , г де г§ =

2GGM - раддус Шва.рц-

тильда.. Ds - расстояние между iicto^tiiiiikom ii ііаблтода.телем. Dd - расстояние между линзой ii иа.блтода.телем.

Dds - расстояние между линзой ii iicto^tiiiiikom.

¹⁷Аналоги радиуса Хвольсона-Эйнштейна в ТЭ: £io 「 2 = 4£°

ξ0 Veff

rs   c

c2    rs Ds

[ ± 丄十 у¹ 十 Vff 32DdsDd ]'

Рис. 4. Крест Эйнштейна: изображение квазара(НиЬЫе NASA/ESA); изображение галактики-линзы ;

аналоги радиуса Хваольсона-Эйнштейна (отмечены стрелками)

Рис. 5. а - числовой расчет (точный вид деталей в центре зависит от шага вычисления, но они всегда присутствуют); b - галактика NGC-1365 (телескоп «Хаббл», NASA/ESA); с - детали, открытые орбитальной обсерваторией Herschel в центре Млечного пути (источник - «Асторофизический журнал» (ApJ))

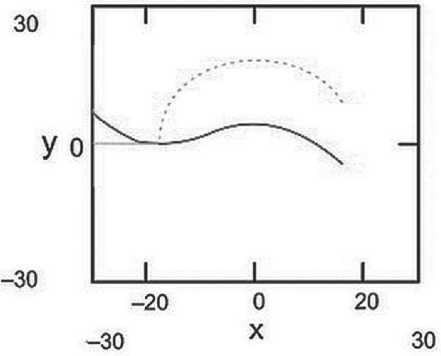
Рис. 6. Дуга окружности соответствует положению эффективного кругового тока массы, тело движется справа налево

Обратим внимание также и на центральную деталь, имеющуюся на расчетном графике. Ее конкретный вид зависит от выбранного шага при счете, она всегда присутствует при расчетах и поначалу вызывала беспокойство своим возможным искусственным характером. Однако после появления новых (май 2011) результатов наблюдений оказалось, что ее можно интерпретировать с учетом изображений, полученных с помощью космической обсерватории «Гершель» (ср. рис.5а и 5с) при фотографировании центра нашей галактики. Да и сходство ее вида с центральной частью фотографии на рис.5Ь может оказаться не случайным.

На рис.6 представлена траектория пробного тела, рассеивающегося на системе цпт в ее плоскости и имеющего два отклонения разного знака, что связано с начальным направлением движения тела и с направлением тока массы. С точки зрения преломления света это означает, что ТЭ предсказывает существование рассеивающих гравитационных линз, которые уменьшают угловой размер находящихся за ними объектов. Так что, если подобная линза находится между объектом и наблюдателем на Земле и ориентирована соответствующим образом, то оценка расстояния до объекта может быть завышенной. Если этот объект -галактика, светимость которой сравнивается со стандартной свечей, то такая ситуация может послужить причиной неправильной интерпретации результатов наблюдений последнего десятилетия, связанных с измерением расстояния до галактик по измерениям наблюдаемой светимости. Именно в связи с наблюдениями их спектров и оценками этих расстояний было сделано предположение о нарушении линейного закона Хаббла. Эти наблюдения и привели к представлению об ускоренном расширении Вселенной и введению понятия темная энергия (отталкивания), которая обеспечивает это ускорение. Не исключено, что интерпретация наблюдений светимости галактик с учетом возможного существования рассеивающих гравитационных линз, позволит не требовать от Вселенной существования не только темной материи, но и темной энергии. Это, однако, нуждается в более тщательной проверке.

6.    Область применимости, интерпретация наблюдений и космологическая картина

Как уже упоминалось в начале предыдущего раздела, для определения области применимости ТЭ следует сопоставить между собой вклады слагаемых гравитационной силы и найти, где они будут иметь одинаковый порядок. Общий вид такого соотношения будет включать характерные параметры ТЭ - фундаментальную скорость и фундаментальную длину, возникшие в связи с переходом к новой модели физической реальности, т.е. к фазовому пространству-времени. Если за фундаментальную скорость принять скорость света с, а за фундаментальную длину - отношение с/Н, где Н - постоянная Хаббла, то тогда мы получим не только соответствие расчетной и наблюдаемой области применимости, но и добавка к гравитационной силе, возникающая в ТЭ на галактических расстояниях, окажется пропорциональна ускорению сН. Это соответствует эмпирической константе, введенной в МОНД с целью подгона к опытным данным, и указывает на то, что совпадение ее величины с сН является не случайным. Одновременно, из теории исключается «лишняя» новая мировая константа, на введении которой настаивает МОНД.

Можно показать, что упоминавшийся выше «логарифмический потенциал» гравитационных сил действующих в спиральной галактике, возникавший в связи с эвристическими соображениями, теперь также следует из вида второго слагаемого для силы, полученного в рамках ТЭ. Таким образом, в этой теории он получает метрическое обоснование.

Таким образом, можно констатировать, что многие проблемы ОТО на галактическом масштабе потеряли свою остроту при использовании нового подхода, связанного с использованием ТЭ. При этом введение новых сущностей оказалось излишним, - по крайней мере, в отношении темной материи это вызывает мало сомнений. Ясно, что все рассуждения, касавшиеся одной галактики, можно повторить и для их кластеров. Что же касается темной энергии, то, хотя проверка и необходима, сам подход, связывающий наблюдаемое действие сил отталкивания с силами, «родственными» силам инерции, все же вызывает меньше недоумения, чем представления о квинтэссенции или 5-й фундаментальной силе, поиск которых пока ни к чему не привел.

Это же соображение о наблюдаемом эффекте относится и к рассуждениям о радиусе кривизны пустого пространства-времени (Де Ситтера). Кажется очевидным, что они противоречат физическому принципу, введенному Эйнштейном, согласно которому (наблюдаемую) кривизну пространства порождает распределение тяготеющих масс. Кривизна же пустого пространства, т.е. не содержащего никаких масс, представляется математической абстракцией, недоступной для наблюдения и измерения.

Обобщая полученные результаты в единое целое, можно обнаружить, что при интерпретации результатов разнообразных наблюдений на основе ТЭ постепенно формируется новая космологическая картина, несколько отличающаяся от предыдущей. Сначала обозначим характерные черты последней, возникшие в связи с построением ОТО. Эйнштейн попытался описать наблюдаемую стационарную Вселенную. С этой целью ему пришлось ввести космологическую постоянную, физическое содержание которой осталось неясным, а решение, получаемое с ее помощью, было неустойчивым. Именно по этой (последней) причине он впоследствии считал эту свою попытку «самой большой ошибкой». Затем стали появляться точные решения, для которых находились и наблюдения, допускающие соответствующую интерпретацию. Это привело к представлениям о существовании черных дыр, о нестационарности (расширении) Вселенной, о Большом Взрыве, о существовании ненаблюдаемой темной материи, об ускорении расширения Вселенной и о темной энергии, связанной с фундаментальным взаимодействием отталкивания. Рассматривая все эти понятия непредвзято, можно отметить, что если попытаться отказаться от них, то наиболее трудно будет обойтись без Большого Взрыва. Представление о его существовании лежит в основе объяснения сразу двух важных наблюдаемых эффектов: красного смещения Хаббла и реликтового радиоизлучения. Остальные понятия, несмотря на их общеупотребительный характер, имеют внутренние противоречия и альтернативы. В частности, при использовании внутренней задачи Шварцшильда для моделирования массивных однородных сферически симметричных объектов, как это иногда делается, возникновение черных дыр может оказаться невозможным уже в рамках самой ОТО18. Гипотеза темной материи оказывается необязательной в ТЭ. Отклонение от линейности в законе Хаббла при наблюдениях, основанных на измерениях светимости галактик, может быть связано с неправильным определением расстояний до них (рассеивающие гравитационные линзы в ТЭ). Да и сам закон Хаббла может соответствовать как равномерному расширению Вселенной (эффект Доплера), так и гравитационному красному смещению, обусловленному тангенциальным движением ее удаленных частей, которое следует из ТЭ и непосредственно предсказывает линейный закон роста красного смещения с расстоянием от наблюдателя19. При этом разброс тангенциальных скоростей удаленных частей Вселенной приведет к появлению разброса точек на экспериментальном графике. При недостаточном их количестве такой разброс также можно принять и за отклонение от (линейного) закона. Таким образом, «темная энергия» отталкивания может оказаться связанной с аналогом (!) «центробежной потенциальной энергии», действие которого и наблюдается.

Переходя к космологической картине, связанной с ТЭ, можно отметить, что ее особенностью является то, что на масштабах галактик и выше главную роль начинают играть тангенциальные движения материи. При этом на масштабах звезд и планетных систем все выводы и предсказания ОТО сохраняются с большой точностью. При сопоставлении наблюдений с моделью анизотропного пространства ТЭ в гравитационном взаимодействии начинают прослеживаться черты, которые традиционно связывались с инерцией. Это приводит к появлению наблюдаемых «сил отталкивания», не имеющих характера пятой фундаментальной силы, исключить которые из наблюдений или отделить от классических гравитационных сил не представляется возможным. Наблюдаемая Вселенная напоминает среду с развитой турбулентностью и взаимодействующими вихрями различных масштабов, имеющих различные времена существования. Это по-новому освещает имеющиеся представления о распределении энергии между светящимися телами (классическая гравитация в ОТО) и их конвективным движением во Вселенной. В целом такая картина оказывается экономнее, удовлетворительно описывает не только явления масштаба планетных систем, где классическая ОТО работает отлично, но и те наблюдения на галактическом масштабе, с которыми она не справляется. При этом ТЭ требует не привлечения новых сущностей, а использования другой модели для описания физической реальности - фазового пространства-времени. Это приводит к интенсивному использованию еще одного раздела математики для исследования физических явлений в масштабах Вселенной.