Теория кернера трех фаз в транспортном потоке - новый теоретический базис для интеллектуальных транспортных технологий
Автор: Кленов С.Л.
Журнал: Труды Московского физико-технического института @trudy-mipt
Статья в выпуске: 4 (8) т.2, 2010 года.
Бесплатный доступ
Кратко рассматриваются основные положения и результаты предложенной Кернером тео- рии трех фаз в транспортном потоке. Эта теория позволяет объяснить и предсказать эм- пирические пространственно-временные свойства перехода кплотному потоку и результи- рующих структур в плотном транспортном потоке. Приводятся результаты измерения про- странственно-временные структур в транспортном потоке на скоростных автомагистралях в Германии, Англии и США. Эти результаты являются эмпирическим базисом как для опре- деления фаз транспортного потока, так и для остальных положений теории Кернера. По- казывается, что в теории Кернера возникновение плотного транспортного потока (traffic breakdown) объясняется как фазовый переход первого рода от фазы свободного потока к фа- зе синхронизованного потока. Такой переход с некоторой вероятностью может происходить в широком диапазоне значений транспортного потока, что отвечает бесконечному числу зна- чений пропускной способности автодороги. Анализируются характерные свойства процесса образования фазы движущихся кластеров машин (движущихся заторов) в синхронизован- ном потоке, дается классификация пространственно-временных структур транспортного потока в теории Кернера. Приводятся примеры новых интеллектуальных транспортных технологий, основанные на теории трех фаз Кернера.
Короткий адрес: https://sciup.org/142185706
IDR: 142185706
Текст научной статьи Теория кернера трех фаз в транспортном потоке - новый теоретический базис для интеллектуальных транспортных технологий
-
I. Введение. Фундаментальные эмпирические свойства фазовых переходов в транспортном потоке
В 1996--2002 годах Кернер с сотрудниками концерна Даймлер провели детальные исследования эмпирических данных, измеренных с помощью датчиков на многочисленных скоростных автомагистралях мира (в Германии, Голландии, Англии, США). Главный результат этих исследований был сформулирован в предисловии к книге Кернера [1]:
Теории транспортного потока и математические модели, которые доминируют в настоящее время в научных журналах и учебных курсах большинства университетов, не могут объяснить ни сам переход от свободному к плотному потоку (traffic breakdown), ни основные свойства возникающих в результате этого перехода структур транспортного потока.
Поэтому Кернер предложил и разработал альтернативную теорию транспортных потоков, названную теорией трех фаз, которая может предсказать и объяснить эмпирические свойства перехода к плотному потоку (traffic breakdown) и результирующих пространственно-временных структур в транспортном потоке. Как достижения, так и критика предшествующих классических подходов к теории транспортных потоков представлены в главе 10 книги Кернера [1]. В на- стоящей статье кратко излагаются основные положения теории трех фаз Кернера в соответствии с книгами [1, 2].
Цель данной статьи состоит в том, чтобы дать представление об эмпирическом базисе и основных идеях теории трех фаз Кернера. Это означает, что статья не может заменить книг Кернера, чтение которых необходимо тем, кто хочет разобраться в этой теории. По этой причине основное внимание уделяется не математическому обоснованию тех или иных положений теории трех фаз Кернера, а качественному описанию. Единственное исключение составляет раздел XII, в котором кратко описана стохастическая трехфазная модель в рамках теории трех фаз и некоторые ее решения. Для более подробного ознакомления с математическими результатами теории трех фаз Кернера рекомендуется прочитать главу 11 книги [1] и часть Ш книги [2].
Прежде чем перейти к изложению некоторых положений теории трех фаз Кернера, важно подчеркнуть фундаментальные достижения предыдущих моделей транспортного потока по математической формулировке многочисленных эффектов взаимодействия между водителями [3--25]. К ним относятся, в первую очередь, введенная в моделях Дженерал Моторс задержка водителей [10--13], приводящая к переторможению как реакции на замедление машины впереди [13, 19, 20], формулировка задержки водителей через модельные флуктуации, введенные в моделях Нагеля, Шрекенбер- га и Шашнайдера (см. обзоры [19--22]), микроскопическое описание slow-to-start rule в работах группы Шрекенберга (см. обзоры [19--22]). Эти и другие математические формулировки в поведении водителя являются также важными элементами математических моделей трех фаз (см. главу 11 книги Кернера [1]).
Несмотря на эти достижения, как было сказано выше, предшествующие модели не могут объяснить ни сам переход от свободного к плотному потоку, ни основные свойства возникающих пространственно-временных структур, наблюдаемых в эмпирических данных. Детальное объяснение этого «парадокса» дано в главе 10 книги Кернера [1]. Этот парадокс объясняется очень просто: анализ эмпирических данных, который позволил выявить фундаментальные эмпирические свойства перехода от свободного к плотному потоку и основные свойства результирующих пространственно-временных структур, стал возможным только в конце 90-х годов, когда стало доступным огромное количество данных измерений со скоростных магистралей Германии и Голландии. Иными словами, выдающиеся ученые, которые создали многочисленные модели транспортного потока, перечисленные выше и многие другие, просто не могли знать, какими же реальными свойствами обладает переход от свободного к плотному транспортному потоку.
Эти фундаментальные эмпирические пространственно-временные свойства перехода от свободного к плотному потоку, а также другие фундаментальные эмпирические свойства фазовых переходов в транспортном потоке, обнаруженные Кернером, детально описаны в разделе 2.4 и части II первой книги Кернера [2]. В рамках данной статьи нет возможности останавливаться на рассмотрении всех эмпирических свойств транспортного потока. Тем не менее сформулируем сначала фундаментальные эмпирические свойства перехода к плотному транспортному потоку и эмпирические свойства фазовых переходов в транспортном потоке.
Фундаментальные эмпирические свойства перехода к плотному транспортному потоку следующие:
-
1. Переход к плотному транспортному потоку (traffic breakdown) является F → S переходом (буква F соответствует «free flow», то есть свободному потоку, буква S обозначает фазу синхронизованного потока, в английской литературе «synchronized flow»).
-
2. Вероятность спонтанного F → S перехода является растущей функцией величины потока машин.
-
3. Может быть как спонтанный, так и индуцированный F → S переход около одного и того же узкого места на дороге (bottleneck).
В главе 10 своей последней книги [1] Кернер показывает, что теория Лайтхилла–Уизема–Ричард- са (ЛВР) кинематических и ударных волн в транспортном потоке [3--5], дискретной версией которой является sell transmission модель Даганцо [9], не может описывать пункты 2 и 3, а модели, относящиеся к классу Дженерал Моторс (см. главу 10 в [1] и обзоры [19--22]), не могут описывать пункты 1--3.
Фундаментальные эмпирические свойства фазовых переходов в транспортном потоке следующие:
-
а) в соответствии с пунктами 1--3, указанными выше, переход от свободного к плотному транспортному потоку (traffic breakdown) является F → S фазовым переходом I рода;
-
б) широкие движущиеся кластеры машин (wide moving jams, обозначается ниже буквой J ) возникают спонтанно только в синхронизованном потоке, то есть в результате последовательности F → S → J фазовых переходов;
-
в) S → J фазовый переход происходит позднее и часто совсем в другом месте, чем F → S фазовый переход.
ЛВР теория кинематических волн не может описывать пункты б) и в), а теория, основанная на моделях класса Дженерал Моторс, не может описывать пункты а)--в).
-
II. Три фазы транспортного потока
Теория трех фаз, основанная Кернером, фокусируется главным образом на физике плотного транспортного потока на скоростных автомагистралях. Кернер описывает три фазы транспортного потока, в то время как классические теории, базирующиеся на фундаментальной диаграмме транспортного потока, рассматривают две фазы: свободный поток и так называемый плотный поток (congested traffic в английской терминологии). Согласно Кернеру в плотном потоке выделяются две фазы, соответственно существуют три фазы транспортного потока:
-
1) свободный поток — фаза F ,
-
2) синхронизованный поток — фаза S ,
-
3) широкий движущийся кластер (локальный движущийся затор, в английской литературе wide moving jam) — фаза J .
Фаза определяется как некоторое состояние транспортного потока, рассматриваемое в пространстве и времени.
Следует подчеркнуть, что в теории трех фаз Кернера разделение на свободный и плотный поток точно такое же, как и в классических теориях Лайтхилла–Уизема и Дженерал Моторс. Фундаментальное отличие теории Кернера состоит в том, что он выделяет две фазы в плотном потоке на основе общих эмпирических пространственновременных свойств транспортного потока, которые за все годы измерений остаются одни и те же на разных автодорогах мира. Другими словами, как определение фаз транспортного потока, так и остальные положения теории, приведенные в разделах II--XI, основаны исключительно на эмпирических данных.
-
III. Свободный транспортный поток — фаза F
В свободном транспортном потоке достаточно малой плотности водители могут практически свободно установить желаемую для них скорость. Эмпирические данные, относящиеся к свободному потоку, показывают положительную корреляцию между величиной потока q , измеряемой в количестве машин в единицу времени (проходящих через данную точку дороги), и плотностью ρ , измеряемой в количестве машин на единицу длины дороги [14, 15]. Зависимость потока q от плотности ρ для свободного потока ограничена максимальным значением величины потока q = q max и соответствующим критическим значением плотности ρ = ρ crit (рис. 1), которые могут быть достигнуты в свободном потоке.
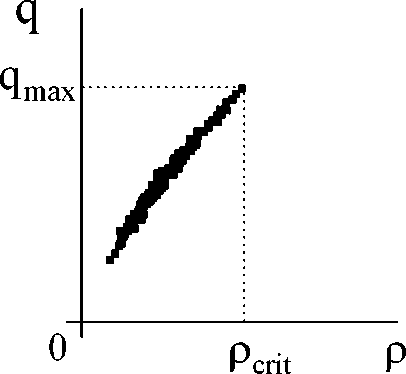
Рис. 1. Величина потока q в зависимости от плотности машин ρ в свободном потоке [14, 20]
-
IV. Плотный транспортный поток
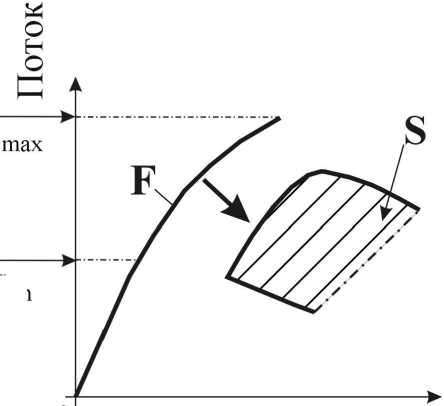
В плотном транспортном потоке, который определяется так же, как и в классических теориях Лайтхилла–Уизема и Дженерал Моторс, скорость машин меньше, чем минимально возможная скорость машин в свободном потоке. Это означает, что прямая с наклоном, равным минимальной скорости в свободном транспортом потоке, (штриховая линия на рис. 2) разделяет все эмпирические данные (точки) на плоскости поток–плотность на две области: слева от этой прямой находятся данные, относящиеся к свободному потоку, а справа — данные, относящиеся к плотному потоку.
Как следует из данных измерений, возникновение плотного потока обычно происходит вблизи неоднородности на автомагистрали, вызванной въездом на автомагистраль, съездом с нее, изменением числа полос, сужением дороги, подъемом, и т.п. Такого типа неоднородность, вблизи которой может происходить переход к плотному транс- портному потоку, в дальнейшем будет называться узким местом, или «бутылочным горлом» [14, 20].
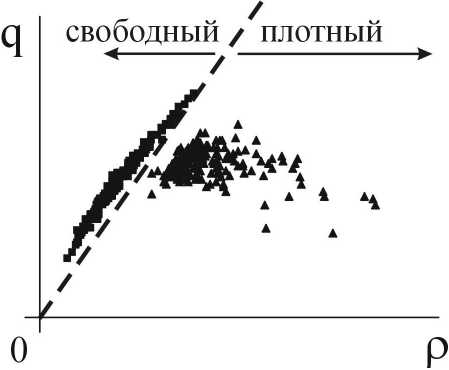
Рис. 2. Величина потока q в зависимости от плотности машин ρ в свободном и плотном потоке [14, 20]
-
V. Определение фазJ и S в плотном транспортном потоке
Кернер показал, что фундаментальная диаграмма и ее применения в том виде, как они используются в классических теориях транспортного потока, неадекватным образом описывают сложную динамику в плотном транспортном потоке. Он выделяет, таким образом, в плотном транспортном потоке фазу S синхронизованного потока, в англоязычной литературе «synchronized flow», и фазу J широкого движущегося кластера (локальный движущийся затор) — «wide moving jam».
Определение фаз J и S в плотном потоке является результатом общих пространственно-временных свойств реальных данных, полученных в результате ежедневных измерений параметров транспортного потока во многих странах на различных скоростных автодорогах в течение многих лет. Кернер определил фазы J и S следующим образом.
Определение [J] фазы широкого движущегося кластера:
Задний по направлению движения фронт широкого движущегося кластера (локального движущегося затора), где машины, выезжающие из кластера, ускоряются вплоть до свободного или до синхронизованного потока, движется против потока с постоянной средней скоростью v g , проходя через все узкие места на скоростной автомагистрали. Это характеристическое свойство широкого движущегося кластера.
Определение [S] фазы синхронизованного потока:
Задний по направлению движения фронт области синхронизованного потока, где машины ускоряются вплоть до свободного потока, НЕ обладает характеристическим свойством широкого движущегося кластера. В частности, задний фронт синхронизованного потока часто фиксирован вблизи узкого места на скоростной автомагистрали.
Необходимо подчеркнуть, что определение фаз J и S вытекает из эмпирических пространственно-временных свойств плотного потока, то есть исходно не имеет никакого отношения к какой-либо математике. Теоретический смысл этих определений можно понять, прочтя раздел 6.1 книги Кернера [1].
Данные измерений средней скорости машин (рис. 3а) иллюстрируют определения фаз J и S . На рис. 3а имеются две пространственно-временные структуры плотного потока с низкой скоростью машин. Одна из них распространяется против потока с почти постоянной скоростью заднего фронта через все узкие места на скоростной автомагистрали. Согласно определению [J], эта область плотного потока относится к фазе «широкого движущегося кластера». Напротив, задний фронт другой области плотного потока фиксирован вблизи места съезда машин с автомагистрали. Согласно определению [S], эта область плотного потока относится к фазе «синхронизованного потока» (рис. 3а и 3б).
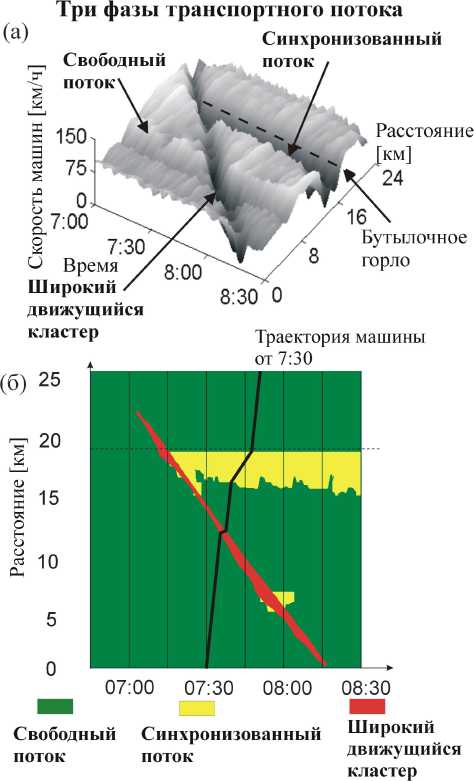
Рис. 3. Данные измерений скорости машин в простран- стве и времени (а) и их представление на координатновременной плоскости (б). Взято из книги Кернера [1]
-
VI. Возникновение плотного потока (traffic breakdown) — F → S фазовый переход
Переход от свободного к плотному потоку в англоязычной литературе известен как traffic breakdown. В теории трех фаз Кернера такой переход объясняется возникновением фазы синхронизованного потока, то есть F → S фазовым переходом. Такое объяснение основывается на имеющихся данных измерений, которые показывают, что после возникновения плотного потока вблизи узкого места на автомагистрали задний фронт возникшего плотного потока фиксирован вблизи этого узкого места. Таким образом, возникший плотный поток удовлетворяет определению [S] фазы синхронизованного потока.
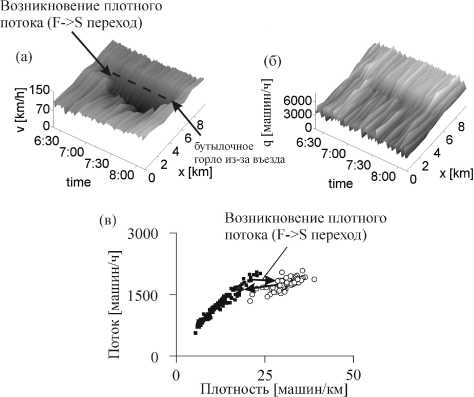
Рис. 4. Эмпирический пример возникновения плотно- го потока и эффект гистерезиса у бутылочного горла из-за въезда на автодорогу. (а, б) Средняя скорость (а) и поток (б) на автодороге в пространстве и времени (увеличение потока после въезда на (б) связано с потоком въезжающих на дорогу машин). (в) Эффект гистерезиса в плоскости поток–плотность, обо- значенный двумя стрелками, показывающими переход к плотному потоку и обратный переход к свободному потоку. 1-минутные данные. Взято из книги Кернера [1]
В самом деле, типичный пример перехода из свободного в синхронизованный поток вблизи въезда машин показан на рис. 4. Из рисунка видно, что в то время как скорость машин резко уменьшается в процессе перехода (рис. 4а), поток меняется мало (рис. 4б). Скачок скорости при мало меняющемся потоке особенно наглядно виден на рис. 4в. В течение всего времени после перехода задний фронт между плотным и свободным потоками фиксирован вблизи въезда на дорогу. По этой причине плотный поток соответствует определению фазы синхронизованного потока, поэтому весь плотный поток относиться к фазе синхронизованного потока. Образование плотного потока примерно в 6:30 мин (показанное стрелкой слева направо на рис. 4в) и его исчезновение примерно в 7:45 (показанное стрелкой справа налево на рис. 4в) сопровождается гистерезисом, хорошо известным в теории фазовых переходов I рода, наблюдаемых в широком классе неравновесных физических, химических и биологических систем. Это свойство F → S фазового перехода является общим свойством реального (эмпирического) транспортного потока, который также представляет собой сложную сильно неравновесную систему.
Второй эмпирический пример перехода к плотному потоку показан на рис 5. На этом примере можно видеть, как в реальном транспортном потоке образуются широкие движущиеся кластеры (рис. 5б, координата дороги x = 0 км). Видно, что в результате перехода к плотному потоку на узком месте, связанным с въездом на скоростную магистраль, сначала образуется фаза S синхронизованного потока. Действительно, в течение всего времени существования плотного потока на этом узком месте задний фронт плотного потока, на котором машины ускоряются из плотного потока до свободного, фиксирован на данном месте. Поэтому по определению фаз в теории Кернера в результате перехода к плотному потоку образуется фаза синхронизованного потока. Другими словами, плотный поток образуется в результате F → S перехода. Напротив, широкие движущиеся кластеры возникают позднее, уже внутри фазы синхронизованного потока. Этот F → S фазовый переход будет рассмотрен ниже, в разделе X.
Таким образом, переход от свободного к плотному потоку в эмпирических данных является F → S переход первого рода. Это эмпирическое свойство есть общее свойство реальных транспортных потоков на скоростных магистралях. Напротив, в моделях класса Дженерал Моторс, как объяснено в книге Кернера [1], переход от свободного к плотному потоку связан с возникновением широких движущихся кластеров.
Используя данные измерений, Кернер сделал вывод, что синхронизованный поток может возникать в свободном потоке спонтанно (спонтанный F → S переход) или индуцированным образом (индуцированный F → S переход). Спонтанный F → S переход означает, что переход к синхронизованному потоку происходит в случае, когда до момента перехода в окрестности узкого места существует свободный поток, а сам фазовый переход происходит в результате роста внутреннего возмущения транспортного потока. В противоположность этому индуцированный F → S переход происходит из-за возмущения транспортного потока, которое первоначально возникает на некотором удалении от положения узкого места, и затем по мере распространения достигает окрестности узкого места. Обычно индуцированный F → S переход связан с распространением в направлении против потока области синхронизованного пото- ка или же широкого движущегося кластера, которые первоначально возникли вблизи следующего в направлении потока узкого места. Эмпирический пример индуцированного фазового перехода, приводящего к возникновению синхронизованного потока, показан на рис. 3: синхронизованный поток возникает благодаря распространению против потока широкого движущегося кластера.
Возникновение плотного
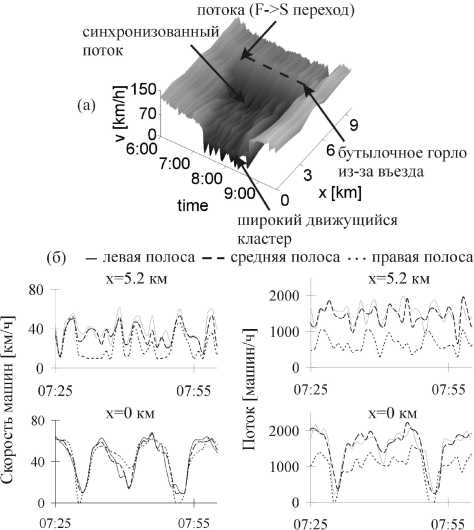
Рис. 5. Эмпирический пример возникновения широ- ких движущихся кластеров в синхронизованном потоке: (а) Скорость машин в пространстве и времени: (б) Скорость (слева) и поток (справа) на трех полосах дороги в области синхронизованного потока (x = 5.2 км) и в области широких движущихся кластеров (x = 0 км). Взято из книги Кернера [1]
Кернер объяснил природу F → S фазового перехода с помощью «соревнования» во времени и пространстве двух противоположных процессов: ускорения машины при обгоне более медленной машины впереди, названном «переускорением», и в случае, когда обгон невозможен, торможения машины до скорости более медленной машины, названном «адаптация скорости». «Переускорение» поддерживает дальнейшее существование свободного потока. Напротив, «адаптация скорости» ведет к синхронизованного потоку. Кернер постулировал, что вероятность обгона, которая совпадает с вероятностью «переускорения», является разрывной функцией плотности (рис. 6): при данной плотности машин вероятность обгона в свободном потоке много больше, чем в синхронизованном потоке.
Разрывная функция вероятности обгона является одной и той же как для спонтанного, так и для индуцированного F → S фазового перехода: термины «спонтанный» и «индуцированный» отличаются только источником возмущения, приводящего к F → S фазовому переходу. F → S пере- ход происходит при условии, что вероятность обгона внутри возмущения в свободном потоке меньше, чем критическая вероятность. Эта критическая вероятность показана пунктирной линией на рис. 6. Другими словами, не имеет значения, будет ли это критическое значение вероятности обгона достигнуто благодаря возмущению в свободном потоке (спонтанный переход) или благодаря распространению до узкого места некоторого возмущения, возникшего ранее в другой области дороги (индуцированный переход).
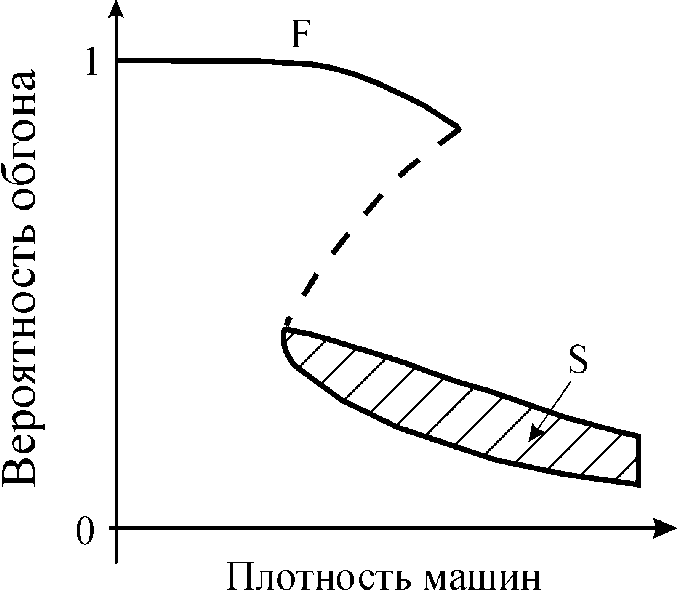
Рис. 6. Объяснение фазового перехода к плотному потоку (traffic breakdown) на основе Z-образной нелинейной функции вероятности обгона (вероятности «пе-реускорения») в теории Кернера. Пунктирная линия описывает критическое значение вероятности обгона как функцию плотности машин. Взято из книги Кернера [1]
Отметим, что F → S фазовый переход и обратный S → F фазовый переход сопровождаются гистерезисом. Однако данный гистерезис не имеет никакого отношения к хорошо известному гистерезису в математических моделях класса Дже-нерал Моторс, впервые найденному в теории Кер-нера–Конхойзера [26, 27]. Этот известный гистерезис, описанный в огромном количестве математических работ (см. работы [19--22, 28, 29] и ссылки в них), описывает F → J и обратный J → F фазовый переход. Как уже несколько раз отмечалось, спонтанный F → J переход не наблюдается в реальном транспортном потоке.
-
VII. Бесконечное число пропускных способностей скоростной автомагистрали
Спонтанное образование плотного потока, то есть спонтанный F → S фазовый переход, может произойти в широком диапазоне значений величины потока q в свободном транспортном потоке. Основываясь на эмпирических данных измерений, Кернер сделал вывод, что существует бесконечное число значений пропускной способности автомагистрали в свободном потоке. Это бесконечное число значений пропускной способности находится в диапазоне между минимальным qth и максимальным qmax значениями пропускной способности (рис. 7).
О тт
Максимум пропускной способности q
Минимум пропускной способности 4th
Плотность машин
Рис. 7. Максимум и минимум пропускной способности скоростной автомагистрали в теории трех фаз Кернера. Взято из книги Кернера [1]
Если величина потока близка к максимальному значению пропускной способности q max , то уже достаточно малое возмущение в свободном потоке вблизи узкого места приведет к спонтанному F → S фазовому переходу. С другой стороны, если величина потока близка к минимальному значению пропускной способности q th , то только возмущение очень большой амплитуды способно привести к спонтанному F → S фазовому переходу.
Вероятность возникновения малых возмущений в свободном транспортном потоке много выше, чем вероятность возникновения возмущений большой амплитуды. По этой причине чем выше величина потока q в свободном потоке вблизи узкого места, тем выше вероятность спонтанного F → S фазового перехода.
Если величина потока q меньше чем минимальная пропускная способность q th , то возникновение плотного потока ( F → S переход) невозможно.
Бесконечное число значений пропускной способности автомагистрали вблизи узкого места может быть объяснено тем, что свободный поток при значениях величины потока q в диапазоне qth С q С qmax является метастабильным. Это означает, что при возникновении малых возмущений свободный поток сохраняется, то есть является устойчивым относительно малых возмущений. Однако для больших возмущений свободный поток оказывается неустойчивым, и происходит F → S фазовый переход к синхронизованному потоку.
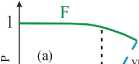
Как уже упоминалось в разделе VI, Кернер объяснил природу F → S фазового перехода с помощью «соревнования» во времени и пространстве двух противоположных процессов: ускорения машины при обгоне более медленной машины впереди, названном «переускорением», и в слу- чае, когда обгон невозможен, торможения машины до скорости более медленной машины, названном «адаптация скорости». На рис. 8 поясняется такое соревнование более детально. На рис. 8а, который соответствует рис. 6, стрелочка вниз означает, что если в свободном потоке вблизи узкого места возникает локальное уменьшение скорости машин, то вероятность обгона внутри этого возмущения падает. Если это уменьшение вероятности обгона становится меньше, чем критическая величина вероятности обгона, показанная пунктирной линией на рис. 8а, то F → S фазовый переход происходит внутри возмущения; в противоположном случае возмущение затухает и свободный поток остается на узком месте. Стрелочка вверх на рис. 8а означает, что если исходное состояние отвечает фазе синхронизованного потока и в этом состоянии возникает случайное локальное увеличение скорости машин, то внутри возмущения вероятность обгона возрастает. Если возрастание вероятности обгона превышает критическое значение (как отмечалось выше, эта критическая вероятность обгона отвечает пунктирной кривой на рис. 8а), то в области возмущения происходит S → F переход; в противоположном случае возмущение затухает, и синхронизованный поток остается.
G
(в) эффект переускорения:
вместо режима следования за машиной впереди - ускорение, чтобы сменить полосу и обогнать
(б) эффект адаптации скорости:
замедление к скорости машины впереди в пределах дистанции синхронизации G вероятности
7 адаптации скорости увеличение вероятности переускорения
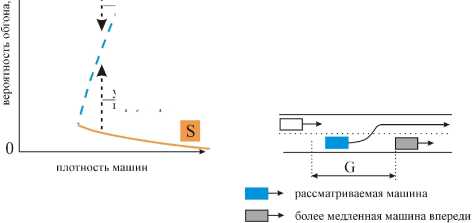
Рис. 8. Пояснение соревнования между переускорени- ем и адаптацией скорости, которое объясняет беско- нечное число значений пропускной способности автомагистрали. Взято из книги Кернера [1]
Бесконечное число значений пропускной способности автомагистрали вблизи узкого места в теории трех фаз Кернера фундаментально противоречит классическим теориям транспортного потока и методам управления и автоматического регулирования транспортных потоков, которые предполагают существование в любой момент времени некоторой (фиксированной или случайной) пропускной способности.
-
VIII. Широкие движущиеся кластеры (локальные движущиеся заторы) — фаза J
Широкий движущийся кластер может быть назван широким только при условии, что его ширина (вдоль дороги) заметно превышает ширину фронтов кластера. Средняя скорость движения машин внутри широкого движущегося кластера много меньше, чем скорость машин в свободном потоке. На заднем (в направлении потока) фронте кластера машины могут ускоряться вплоть до свободного потока. На переднем фронте кластера машины, подъезжающие к фронту, должны сильно уменьшать свою скорость. Согласно определению фазы J , широкий движущийся кластер обычно сохраняет среднюю скорость заднего фронта vg , даже если кластер проходит через другие фазы транспортного потока и узкие места. Величина потока сильно падает внутри широкого движущегося кластера.
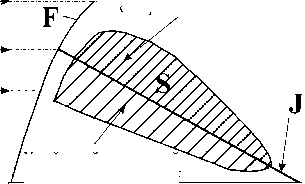
Эмпирические результаты показывают (см. часть II в книге [2] и ссылки в ней), что характеристические параметры широких движущихся кластеров не зависят от величины потока на дороге и особенностей узкого места (где и когда кластер возник). Однако характеристические параметры зависят от погоды, дорожных условий, конструктивных характеристик машин, процента длинных машин и т.п. Скорость заднего фронта широкого движущегося кластера v g в противоположном потоку направлении является характеристическим параметром так же, как и величина выходного потока q out из кластера, в случае, когда свободный поток формируется после кластера (рис. 9). Это означает, что разные широкие движущиеся кластеры имеют одинаковые параметры при одинаковых условиях. В результате данные параметры могут быть предсказаны. Движение заднего фронта широкого движущегося кластера может быть показано на плоскости поток — плотность с помощью прямой, называемой линией J Кернера (рис. 9). Наклон линии J Кернера равен скорости заднего фронта v g , в то время как координата пересечения линии J Кернера с осью абсцисс (при нулевом потоке) отвечает плотности машин ρ max в широком движущемся кластере [1].
Максимум § пропускной g способности qmax С
Выходной поток из широкого движущегося ____ кластера qout
Минимум ____ пропускной способности qth
Метастабильный однородный синхронизованный поток
О
Плотность машин
Устойчивый однородный синхронизованный поток
Рис. 9. Три фазы транспортного потока в плоскости поток–плотность в теории трех фаз Кернера. Взято из книги Кернера [1]
Кернер подчеркивает, что минимум пропускной способности qth и величина выходного потока из широкого движущегося кластера qout описывают два качественно различных свойства свободного транспортного потока. Минимум пропускной способности qth характеризует F → S фазовый переход вблизи узкого места, то есть возникновение плотного потока (traffic breakdown). В свою очередь величина выходного потока из широкого движущегося кластера qout характеризует условия существования таких кластеров, то есть фазы J. В зависимости от внешних условий, таких как погода, процент длинных машин в потоке и т.п., а также от характеристик узкого места, вблизи которого возможен F → S фазовый переход, минимум пропускной способности qth может быть как меньше (рис. 9), так и больше чем величина выходного потока qout .
Важно, что величина выходного потока из широкого движущегося кластера q out оказывается меньше, чем максимально возможный поток q max в свободном потоке перед кластером. Это означает, что в свободном потоке водители могут выбирать более короткую временную дистанцию до машины впереди, чем та дистанция, которую они принимают, ускоряясь на заднем фронте широкого движущегося кластера.
-
IX. Синхронизованный транспортный поток — фаза S
В отличие от широких движущихся кластеров, в синхронизованном потоке как величина потока q , так и скорость машин могут меняться заметным образом. Задний по направлению потока фронт синхронизованного потока часто фиксирован в пространстве (см. определение [S]), обычно вблизи расположения узкого места. Величина потока q в фазе синхронизованного потока может оставаться почти такой же, как и в свободном потоке, даже если скорость машин сильно уменьшается.
Синхронизованный поток не имеет характеристического свойства [J] фазы широкого движущегося кластера J . В теории трех фаз Кернера предполагается, что гипотетические однородные состояния синхронизованного потока покрывают двумерную область в плоскости поток–плотность (см. заштрихованную область на рис. 9).
-
X. S → J фазовый переход
Широкие движущиеся кластеры не возникают в свободном потоке, но они могут возникать в области синхронизованного потока. Это называется S → J фазовым переходом. Эмпирический пример S → J перехода показан на рис. 5. Таким образом, образование широких движущихся кластеров в свободном потоке наблюдается в результате каскада F → S → J фазовых переходов: сначала область синхронизованного потока возникает внутри свободного потока. Как было объяснено выше, такой F → S фазовый переход происходит в большинстве случаев вблизи узкого места. Далее внутри синхронизованного потока происходит
«сжатие» потока, то есть плотность машин возрастает, в то время как их скорость падает. Такое сжатие называется «пинч»-эффект. В области синхронизованного потока, где происходит пинч-эффект, возникают узкие движущиеся кластеры. Кернер показал, что частота возникновения узких движущихся кластеров тем выше, чем выше плотность в синхронизованном потоке. По мере того как эти узкие движущиеся кластеры нарастают, некоторые из них трансформируются в широкие движущиеся кластеры, другие же исчезают. Широкие движущиеся кластеры в дальнейшем распространяются против потока, проходя через все области синхронизованного потока и через все узкие места.
Чтобы детальнее проиллюстрировать S → J фазовый переход, следует заметить, что в теории трех фаз Кернера линия J делит все однородные состояния синхронизованного потока на две области (рис. 9). Состояния выше линии J являются метастабильными относительно образования широких движущихся кластеров, в то время как состояния ниже линии J являются устойчивыми. Метастабильные состояния синхронизованного потока означают, что относительно малых возникающих возмущений состояние потока остается устойчивым, однако при больших возмущениях в синхронизованном потоке происходит S → J фазовый переход.
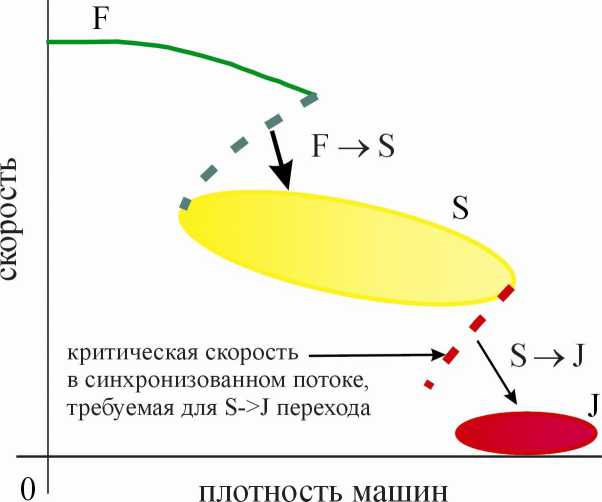
Рис. 10. Двойная Z-характеристика в теории трех фаз Кернера, поясняющая каскад F → S → J фазовых переходов. Взято из книги Кернера [1]
Каскад F → S → J фазовых переходов можно пояснить на основе двойной Z характеристики в теории трех фаз Кернера (рис. 10). Пунктирная линия между фазами F и S качественно соответствует критической скорости внутри локального возмущения свободного потока, при которой происходит F → S фазовый переход. Другими словами, F → S фазовый переход происходит внутри локального возмущения свободного потока, в котором скорость меньше чем критическая скорость (символически этот фазовый переход показан стрелкой между фазами F и S на рис. 10).
Пунктирная линия между фазами S и J качественно соответствует критической скорости внутри локального возмущения синхронизованного потока, при которой происходит S → J фазовый переход. Другими словами, S → J фазовый переход происходит внутри локального возмущения синхронизованного потока, в котором скорость меньше чем критическая скорость (символически переход показан стрелкой между фазами S и J на рис. 10).
-
XI. Неоднородные пространственно-временные структуры транспортного потока, состоящие из фаз S и J
В эмпирических данных можно наблюдать очень сложные пространственно-временные структуры в плотном транспортном потоке, образовавшиеся в результате F → S и S → J фазовых переходов.
Неоднородная пространственно-временная структура, которая состоит только из синхронизованного потока, называется структурой синхронизованного потока (СП). Когда задний фронт СП фиксирован вблизи узкого места на дороге, а передний фронт не распространяется против потока, такая СП называется локализованной структурой синхронизованного потока (ЛСП). Однако во многих случаях передний фронт структуры синхронизованного потока распространяется в направлении против потока. Если при этом задний фронт по-прежнему остается фиксированным вблизи узкого места, то ширина области синхронизованного потока увеличивается. Такая структура называется расширяющейся структурой синхронизованного потока (РСП). Возможна также ситуация, когда задний фронт синхронизованного потока уже не фиксирован вблизи узкого места, а оба фронта синхронизованного потока движутся в направлении против потока. Такая структура называется бегущей, или мигрирующей структурой синхронизованного потока (МСП).
Разница между пространственно-временными структурами, состоящими из только синхронизованного потока, и широкими движущимися кластерами становится особенно ясной, когда РСП или МСП достигают следующего узкого места, расположенного вверх по течению транспортного потока. В таком случае структура синхронизованного потока «захватывается» на этом узком месте (так называемый «catch-effect» в английской терминологии), и возникает новая пространственновременная структура в транспортном потоке. Напротив, широкий движущийся кластер не захватывается вблизи узкого места, а распространяется дальше против потока, то есть пробегая через узкое место на дороге. Кроме того, в отличие от широкого движущегося кластера, структура синхронизованного потока, даже если она распространяется в виде МСП, не имеет характеристических параметров. В результате скорость заднего фронта МСП может заметно меняться в процессе распространения и может быть разной у разных МСП. Данные особенности структур синхронизованного потока и широких движущихся кластеров вытекают из определения фаз S и J .
Наиболее типичная пространственно-временная структура плотного транспортного потока состоит из обеих фаз S и J . Такая структура называется общей структурой плотного потока (ОП).
На многих скоростных автомагистралях узкие места, связанные с въездами / выездами, располагаются очень близко друг к другу. Пространственно-временная структура, в которой синхронизованный поток охватывает два и более узких места, называется единой структурой плотного потока (ЕП). ЕП может состоять только из синхронизованного потока, тогда она называется ЕСП (единая структура синхронизованного потока). Однако обычно широкие движущиеся кластеры возникают в синхронизованном потоке. В этом случае ЕП называется ЕОП (единая общая структура плотного потока) (рис. 11).
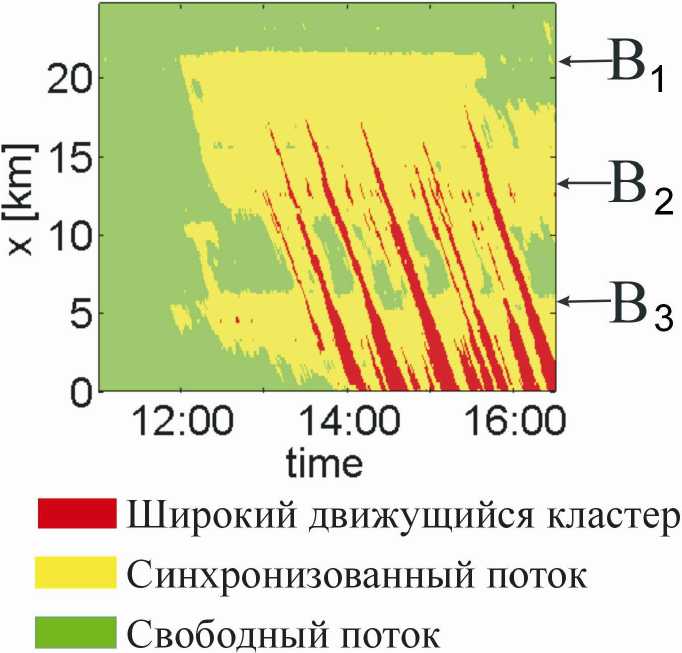
Рис. 11. ЕОП, измеренная на магистрали с тремя узкими местами B 1 , B 2 и B 3 . Взято из книги Кернера [1]
В данном разделе были рассмотрены основные качественные положения теории трех фаз Кернера, которые начиная с 2002 года были использованы как теоретический базис при создании целого ряда микроскопических и макроскопических трехфазных моделей транспортного потока (см. ссылки на оригинальные работы в главе 11 в книге [1]). В следующем разделе дается краткий обзор стохастической микроскопической модели в рамках теории трех фаз Кернера и приведены некоторые результаты численных расчетов.
-
XII. Стохастическая модель в рамках теории трех фаз Кернера
Теория трех фаз Кернера является качественной теорией. Различные математические трехфазные модели транспортных потоков были разработаны в последние годы в рамках теории трех фаз Кернера. Впервые микроскопическая трехфазная модель, которая может воспроизводить эмпирические свойства перехода к плотному потоку (traffic breakdown) и результирующих пространственновременных структур, была разработана Кернером и Кленовым в 2002 году [30]. Несколькими месяцами позже Кернер, Кленов и Вольф предложили трехфазную модель на основе клеточных автоматов (ККВ модель) [31]. Позднее были также разработаны другие модели транспортного потока в рамках теории трех фаз Кернера: Дэвис [32], а также Кернер и Кленов [33] предложили детерминистические микроскопические модели трех фаз; Ли и Шрекенберг с соавторами [34], Янг и Ву [35], и Гао с соавторами [36] разработали различные трехфазные модели клеточных автоматов (КА); Лаваль [37] и Хугендорн с соавторами [38] разработали макроскопические модели трех фаз. Последние результаты моделирования транспортного потока, проведенные различными научными группами в США, Германии, Голландии, Китае, Южной Кореи и Японии в рамках теории трех фаз Кернера, можно найти в [39--62].
В данном разделе кратко рассматривается стохастическая микроскопическая трехфазная модель транспортного потока, предложенная Кернером и Кленовым в [30, 63]. В этой модели [63] использовалось дискретное время с шагом τ ,вто время как перемещение в пространстве предполагалось непрерывным. Ниже будет рассмотрена дискретная версия модели [63], сформулированная в [60], в которой используется достаточно мелкая дискретизация пространства с шагом δx (см. также формулировку дискретной версии модели в [61]). При этом в приведенных ниже формулах координата измеряется в единицах δx , в то время как скорость машины и ее ускорение измеряются соответственно в единицах 6v = 6х/т и 6a = 6v/t , где временной шаг т = 1 сек.
Уравнения движения машины в дискретной версии [60, 61] стохастической трехфазной модели [63] транспортного потока на скоростной 2-полосной автодороге в приближении идентичных машин задаются следующими формулами:
vn+1 = max(0, min(v/ree,v„+i + ^„,v„ + aT,vs,n)), xn+1 xn + vn+1т, (1)
v n +1 = max(0 , min( V free ,V s,n ,V c,n )) , (2)
v c,n =
vn + A n , если gn ^ Gn, Vn + anT, если gn > Gn,
A n = max( - b n T, min( a n T,v t,n — V n )) , (4) где индекс n отвечает дискретному времени t = пт, n = 0 , 1 , 2 , ... ; x n и v n — координата и скорость машины на временном шаге п ; V free — максимальная скорость машины в свободном потоке; g n = x ^,n — x n — d — расстояние до машины впереди, индекс ^ относится ко всем переменным и функциям, описывающим машину впереди, d — длина машины, которая предполагается одинаковой и включает в себя также среднее расстояние между машинами, когда они стоят внутри широкого движущегося кластера; V n — величина скорости машины без шумовой компоненты ^ n ; v s,n — безопасная скорость; a n > 0 и b n ^ 0; a — максимальное ускорение; G n — максимальное расстояние, на котором водитель синхронизует свою скорость со скоростью машины впереди (так называемая дистанция «синхронизации скорости»):
G n = G ( v n ,v ^,n ) , (5) где
G ( u,w ) = max(0 , \_ кти + a - 1 u ( u — w ) J ) , (6) где k > 1 — константа, ^ z J означает целую часть действительного числа z .
Решения модели (1)--(6) при стационарном и однородном движении машин (которое отвечает потоку, где машины находятся на одинаковом расстоянии друг от друга и движутся с постоянной скоростью) показаны на рис. 12а и 12б. В соответствии с фундаментальной гипотезой теории трех фаз Кернера (рис. 9) фаза синхронизованного потока (буква S) как на плоскости расстояние–скорость (рис. 12а), так и на плоскости поток–плотность (рис. 12б) покрывает двумерную область (заштрихованная область на рис. 12). Для того чтобы пояснить смысл этой двумерной области для стационарных состояний синхронизованного потока, рассмотрим более подробно рисунок 12а. Видно, что при некоторой заданной величине скорости v < Vfree в стационарном состоянии существует бесконечное количество расстояний между машинами в диапазоне gsafe < g < G, где g — расстояние между машинами, G = G(v,v) — дистанция синхронизации скорости (5), взятая при одинаковых скоростях машин, gsafe — безопасное расстояние между машинами, которое является решением уравнения v = vs (gsafe), где безопасная скорость vs в однородном стационарном состоянии определяется как vs(g) = g/т. Таким образом, стационарные однородные состояния стохастической трехфазной модели (рис. 12) принципиально отличаются от таких же состояний всех предшествующих моделей, в которых заданной скорости отвечает одно единственное расстояние между машинами, соответствующее точке на фундаментальной диаграмме.
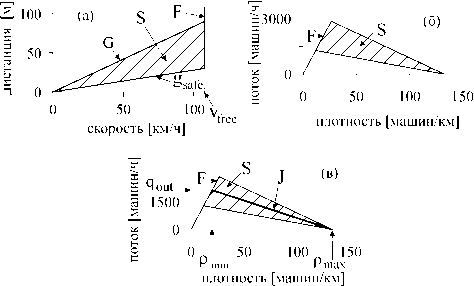
Рис. 12. Стационарные однородные состояния и линия J Кернера в стохастической трехфазной модели: (а, б) свободный поток ( F ) и синхронизованный поток (заштрихованная двумерная область, обозначенная буквой S ) на плоскости расстояние между машинами — скорость (а) и на плоскости поток-плотность (б). На (в) показано соответствие между линией J и однородными стационарными состояниями модели на плоскости поток–плотность
Из рис. 12в видно, что линия J Кернера не имеет никакого отношения к фундаментальной диаграмме стационарного однородного плотного потока в моделях, основанных на фундаментальной диаграмме. Действительно, в трехфазной стохастической модели линия J , которая находится из стационарного движения широкого кластера, разделяет двумерную область стационарных однородных состояний синхронизованного потока на две части. Оказывается, что в соответствии с теорией трех фаз Кернера стационарные однородные состояния выше линии J являются метастабиль-ными к образованию широких движущихся кластеров, а состояния ниже линии J — устойчивыми к образованию широких кластеров.
Чтобы моделировать случайное время задержки водителя как при ускорении, так и при замедлении в различных транспортных ситуациях, величины a n и b n в (3) и (4) задаются как случайные функции:
an = aO (Pо - r 1),
bn = aO (Pi - ri),
P = I Pо, если Sn = 1,
0 [ 1 , если S n = 1 ,
P = Г P 1 , если S n = - 1 ,
-
1 | p 2 , если S n = - 1 ,
где величины 1 — P 0 и 1 — P 1 представляют собой вероятности для времени задержки водителя соответственно при ускорении и при замедлении машины; p о ( v ) и p 2 ( v ) являются функциями скорости машины, p 1 — константа; r 1 = rand (0 , 1) случайная величина, равномерно распределенная в интервале от 0 до 1.
Случайная компонента £n в формуле (1) описывает случайное замедление или ускорение и применяется в зависимости от того, тормозит ли машина или ускоряется, или не меняет свою скорость:
£ n
— £ Ь , если S n +1 = — 1 ,
< £а , если S n +1 = 1 ,
£(0), если Sn+1 =0, где S — состояние движения машины в отсутствие случайной компоненты £n:
S n +1 =
— 1 , если V n +1 < V n , 1 , если V n +1 > V n , 0 , если V n +1 = V n ,
£ a , £ ь являются случайными источниками соответственно для ускорения и замедления машины:
£а = aTO (pa — r),
£b = aTO (pb — r), а случайный источник
£ (0) = a (0) t <
— 1, если r < p(0),
1, если p(0) < r < 2p(0) и Vn > 0, 0 в остальных случаях применяется в отсутствие ускорения или замедления и связан с невозможностью точно поддерживать заданную скорость.
Величины p a и p b являются вероятностями соответственно случайного ускорения или торможения машины, p (0) и a (0) — константы, r = rand (0 , 1), ступенчатая функция O ( z ) определяется как O ( z ) = 0 при z < 0 и O ( z ) = 1 при z > 0.
Безопасная скорость v s,n вычисляется следующим образом:
• / (safe) ( а ) . gn
-
V s,n = min ^ v ( f ) , v ^ 7 + ,
где
V(a) = max(0, min(v(sf), ve,n, ge,nк) — aT)
— так называемая «ожидаемая» (прогнозируемая) скорость машины впереди, функция v ^nsafe ) = ^ v ( safe ) ( g n ,v £,n ) J задается безопасной скоростью v ( safe ) ( g n ,v ^,n ), которая была предложена в модели Краусса с соавторами [64] в 1997 году и которая в свою очередь является решением уравнения Гиппса [65]:
V ( safe) T + Xd (V(safe)) = gn + Xd (Vt,n ) , где Xd(u) — тормозной путь, проходимый машиной, движущейся с первоначальной скоростью u и тормозящей с постоянным ускорением b вплоть до полной остановки. В модели с дискретным временем этот путь дается формулой Xd(u) = Ьт2(ав + 0,5а(а — 1)), а и в — соответственно целая и дробная части величины u/bτ .
В рассматриваемой модели автодороги с двумя полосами смена полосы машинами происходит независимо от того, находятся ли эти машины вдали или вблизи неоднородностей дороги, связанной с въездом/выездом. Машина меняет полосу, если необходимые условия для перехода с правой полосы на левую (R ^ L) или с левой полосы на правую (L ^ R) выполняются совместно с условиями безопасности при смене полосы. Необходимые для смены полосы условия имеют вид
R ^ L : v+ > vg,n + 51 и Vn > v^n,
L ^ R : v+ > V£,H + 51
Условия безопасности при вид или V+ > Vn + 51.
смене полосы имеют
9+ > min(vnT,G+), g- > min(v- T,G- ), (7)
где
G+ = G (vn ,v+), G- = G (v- ,vn), верхние индексы «+» и ««—» относятся соответственно к машинам впереди и позади на соседней полосе.
Если условия (7) не выполняются, то используются более жесткие условия для «вдавливания» машины на соседнюю полосу:
x+ — x- — d> gtmnet, где gtmget = LAv+ + dJ.
(8)
В дополнение к (8) используется условие, что машина проходит среднюю точку x nm ) = L ( x + + x - ) / 2 J между двумя соседними машинами на соседней полосе, то есть выполня-
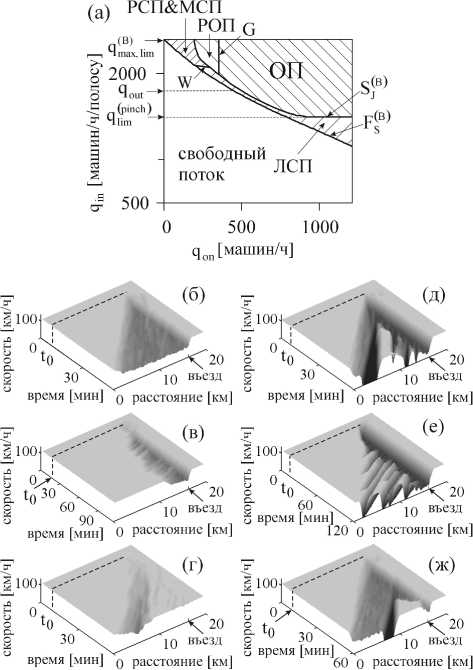
Рис. 13. Диаграмма пространственно-временных структур транспортного потока вблизи изолированного въезда (а) и соответствующие типы пространственно-временных структур (б)--(ж), относящиеся к диаграмме (а): СП (б)--(г) и ОП (д)--(ж) (из книги Кернера [2])
ются следующие условия:
x n
. ( m ) ( m ) ( m )
X n - 1 < xv n _ 1 и X n ^ xn.' или X n - 1 > x n - 1 и
( m )
Если условия для смены полосы выполняются, машина меняет полосу с вероятностью p c < 1 на текущем шаге.
После смены полосы скорость v n устанавливается равной V n = min( v + , v n + A v (1) ), что описывает изменение скорости после маневра по смене полосы. После смены полосы координата машины не меняется, если выполнены условия (7), и
( m )
она устанавливается равной x n = x n , если выполнено условие (8). Величины A v (1) , p c , 5 1 и А являются константами.
Более подробно об использованных параметрах модели, условиях смены полосы и модели поведения водителя на въезде / выезде со скоростной автодороги можно прочитать в главе 11 книги Кернера [1].
На рис. 13 приведены результаты расчета пространственно-временных структур, возникающих вблизи въезда на автодорогу, и областей их существования (диаграммы) на плоскости с координатами: поток по основной дороге q in , приведенный на одну из двух полос дороги, и поток со стороны въезда на дорогу q on .
На рис. 13а показана диаграмма этих пространственно-временных структур. По оси абсцисс данной диаграммы откладывается поток машин q on , по оси ординат указан поток машин по основной дороге q in . Граница F s B ) на диаграмме разделяет свободный поток влево от границы от структур плотного потока, возникающих вблизи въезда машин. На границе F ( B ) пространственновременные структуры плотного потока возникают спонтанно. Граница S JB ) разделяет структуры синхронизованного потока (СП) от общей структуры плотного потока (ОП). Это означает, что
( B ) ( B )
между границами F S и S J возникают различного типа СП. При больших q in и маленьких q on возникает мигрирующая структура плотного потока — МСП (рис. 13г). При увеличении q on МСП превращается в расширяющуюся структуру плотного потока — РСП (рис. 13б). Если уменьшать q in и увеличивать q on , то на границе, обозначенной буквой W , РСП превращаются в локализованную структуру плотного потока — ЛСП (рис. 13в).
Укажем еще некоторые особенности общей структуры плотного потока — ОП, которая возникает выше границы S(B) на диаграмме (область ОП на рис. 13а). Существует граница, обозначенная буквой G внутри области возникновения структур ОП. Слева от этой границы, после того как широкий кластер возникает в синхронизованном потоке, новые широкие кластеры больше не формируются (рис. 13ж), и возникает рассасывающаяся общая структура плотного потока (РОП). Правее от границы G возникает общая структура, в которой непрерывно рождаются новые кластеры внутри синхронизованного потока (рис. 13д). Однако если уменьшать поток по дороге qin , оставаясь в области ОП, и перейти к значениям qin меньше чем qout (поток qout соответствует величине свободного потока, образованного машинами, выезжающими из широкого движущегося кластера), то широкие движущиеся кластеры, спонтанно возникающие в синхронизованном потоке ОП, постепенно рассасываются, распространяясь против течения. В результате возникает ОП, показанная на рис. 13е. Другая особенность общей структуры состоит в том, что если поток из въезда qon дальше увеличивать, то возникает некоторый эффект насыщения, связанный с возникновением плотного потока на дороге, ведущей к въезду машин. Этот эффект насыщения связан с тем, что поток внутри области синхронизованного потока в ОП достигает своего предельного минимального значения, обозначенного на рис. 13а как ql(ipminch).
Распределения скорости и потока внутри ОП структуры на рис. 13д как функции времени при разных координатах вдоль дороги показаны на рис. 14. Можно видеть, что сначала на 16 , 5 км возникает фазовый F → S переход из свободного в синхронизованный поток. Через 2 км против течения ( x = 14 , 5) видно развивающиеся узкие кластеры внутри синхронизованного потока. По мере распространения этих кластеров против течения амплитуда кластеров увеличивается и их ширина возрастает. В результате нарастания кластеров возникает последовательность широких движущихся кластеров ( x = 8 км).
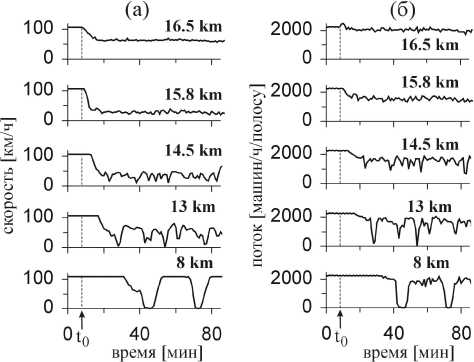
Рис. 14. Одноминутные данные виртуальных детекторов, отвечающие ОП на рис. 13д. Въезд на скоростную дорогу отвечает координате 16 км (из книги Кернера [2])
Более подробно свойства пространственно-временных структур, полученные в результате моде- лирования, рассматриваются в книгах Кернера [1] и [2].
XIII. Применение теории трех фаз Кернера для интеллектуальных транспортных технологий
Кернер с сотрудниками предложил и частично внедрил в эксплуатацию целый ряд новых методов интеллектуальных транспортных технологий. Одним из внедренных и уже установленных на скоростных автодорогах применений теории трех фаз Кернера является метод ASDA / FOTO. Метод ASDA / FOTO функционирует в работающей онлайн-системе регулирования транспортных потоков, где на основе измерений выделяются фазы S и J в плотном транспортном потоке. Распознавание, отслеживание и прогнозирование положений фаз S и J осуществляется на основе методов теории трех фаз Кернера. Метод ASDA / FOTO реализован в компьютерной системе, способной быстро и эффективно обрабатывать большие объемы данных, измеренных датчиками в сети скоростных автомагистралей (см. примеры из трех стран на рис. 15).
Единая общая структура плотного потока (ЕОП)
(а) Автодорога А5-Север (14 июня, 2006) в Германии
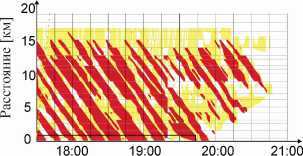
(б) Автодорога М-42 (11 января, 2008) в Великобритании
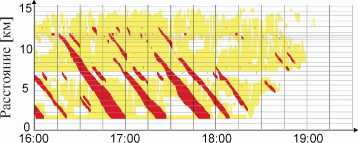
(в) Автодорога 1405-Юг (04 марта, 2003) в США
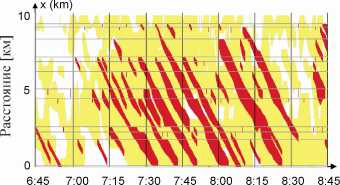
Широкий движущийся кластер Синхронизованный поток
Рис. 15. Пространственно-временная структура транспортного потока, полученная методом ASDA / FOTO в трех странах (из книги Кернера [1])
Дальнейшее развитие приложений теории трех фаз Кернера связано с разработкой и усовершенствованием моделей для транспортных симуляторов, методов регулирования въездного по- тока на автомагистраль (ANCONA), методов коллективного регулирования транспортных потоков, системы автоматического ассистента водителя и методов детектирования состояния транспортного потока, описанных в книгах Кернера [1, 2].
Список литературы Теория кернера трех фаз в транспортном потоке - новый теоретический базис для интеллектуальных транспортных технологий
- Kerner B.S. Introduction to Modern Traffic Flow Theory and Control. -Berlin: Springer, 2009.
- Kerner B.S. The Physics of Traffic. -Berlin: Springer, 2004.
- Lighthill M.J., Whitham G.B. On kinematic waves: II. Theory of traffic flow on long crowded roads//Proc. R. Soc. London. Ser. A. -1955. -V. 229. -P. 281-345.
- Richards P.I. Shock Waves on the Highway//Oper. Res. -1956. -V. 4. -P. 42-51.
- Уизем Дж. Линейные и нелинейные волны. -М.: Мир, 1977.
- Newell G.F. Applications of Queuing Theory. -London: Chapman and Hall, 1982.
- Newell G.F. Nonlinear effects in the dynamics of car-following//Oper. Res. -1961. -V. 9. -P. 209-229.
- Newell G.F. A moving bottleneck//Transp. Res. B. -1998. -V. 32. -P. 531-537.
- Daganzo C.F. The cell transmission model: A dynamic representation of highway traffic consistent with the hydrodynamic theory//Transp. Res. B. -1994. -V. 28, N 4. -P. 269-287.
- Herman R., Montroll E.W., Potts R.B., Rothery R.W. Traffic dynamics: studies in car following//Oper. Res. -1959. -V. 7. -P. 86-106.
- Gazis D.C., Herman R., Potts R.B. Car following theory of steady state traffic flow//Oper. Res. -1959. -V. 7. -P. 499-505.
- Gazis D.C., Herman R., Rothery R.W. Nonlinear follow the leader models of traffic flow//Oper. Res. -1961. -V. 9. -P. 545-567.
- Gazis D.C. Traffic Theory. -Berlin: Springer, 2002.
- May A.D. Traffic Flow Fundamentals. -New York: Englewood Cliffs, Prentice-Hall, 1990.
- Leutzbach W. Introduction to the Theory of Traffic Flow. -Berlin: Springer, 1988.
- Daganzo C.F. Fundamentals of Transportation and Traffic Operations. -New York: Elsevier Science Inc., 1997.
- Mu noz J.C., Daganzo C.F. Moving bottlenecks: a theory grounded on experimental observations//Traffic and Transportation Theory. Ed. by Taylor M.A.P. -Oxford: Pergamon, 2002. -P. 441-462.
- Traffic Flow Theory/Ed. by Gartner N.H., Messer C.J., Rathi A. -Washington, DC: Transportation Research Board, 2001.
- Traffic Flow Theory/Ed. by Gartner N.H., Messer C.J., Rathi A. -Washington, DC: Transportation Research Board, 2001.
- Chowdhury D., Santen L., Schadschneider A. Statistical physics of vehicular traffic and some related systems//Phys. Rep. -2000. -V. 329. -P. 199-329.
- Helbing D. Traffic and related self-driven many particle systems//Rev. Mod. Phys. -2001. -V. 73. -P. 1067-1141.
- Nagatani T. The physics of traffic jams//Rep. Prog. Phys. -2002. -V. 65. -P. 1331-1386.
- Nagel K., Wagner P., Woesler R. Still flowing: Approaches to traffic flow and traffic jam modelling//Oper. Res. -2003. -V. 51. -P. 681-716.
- Mahnke R., Kaupuџs J., Lubashevsky I. Probabilistic description of traffic flow//Phys. Rep. -2005. -V. 408. -P. 1-130.
- Rakha H., Pasumarthy P., Adjerid S. A simplified behavioral vehicle longitudinal motion model//Transp. Lett. -2009. -V. 1. -P. 95-110.
- Delitala M., Tosin A. Mathematical modelling of vehicular traffic: A discrete kinetic theory approach//Math. Models Methods Appl. Sci. -2007. -V. 17. -P. 901-932.
- Kerner B.S., KonhЁauser P. Cluster effect in initially homogeneous traffic flow//Phys. Rev. E. -1993. -V. 48. -P. 2335-2338.
- Kerner B.S., KonhЁauser P. Structure and parameters of clusters in traffic flow//Phys. Rev. E. -1994. -V. 50. -P. 54-83.
- Blank M. Hysteresis phenomenon in deterministic traffic flows//J. Stat. Phys. -2005. -V. 120, N 3-4. -P. 627-658.
- Maerivoet S., De Moor B. Cellular automata models of road traffic//Phys. Rep. -2005. -V. 419, N 1. -P. 1-64.
- Kerner B.S., Klenov S.L. A microscopic model for phase transitions in traffic flow//J. Phys. A: Math. Gen. -2002. -V. 35. -P. L31-L43.
- Kerner B.S., Klenov S.L., Wolf D.E. Cellular automata approach to three-phase traffic theory//J. Phys. A: Math. Gen. -2002. -V. 35. -P. 9971-10013.
- Davis L.C. Multilane simulations of traffic phases//Phys. Rev. E. -2004. -V. 69. -016108.
- Kerner B.S., Klenov S.L. Deterministic microscopic three-phase traffic flow models//J. Phys. A: Math. Gen. -2006. -V. 39. -P. 1775-1809.
- Lee H.K., Barloviж R., Schreckenberg M., Kim D. Mechanical Restriction versus Human Overreaction Triggering Congested Traffic States//Phys. Rev. Lett. -2004. -V. 92. -238702.
- Jiang R., Wu Q.S. Spatial-temporal patterns at an isolated on-ramp in a new cellular automata model based on three-phase traffic theory//J. Phys. A: Math. Gen. -2004. -V. 37. -P. 8197-8213.
- Gao K., Jiang R., Hu S-X., Wang B-H., Wu Q.S. Cellular-automaton model with velocity adaptation in the framework of Kerners three-phase traffic theory//Phys. Rev. E. -2007. -V. 76. -026105.
- Laval J.A. Linking synchronized flow and kinematic waves//Traffic and Granular Flow 05. Ed. by Schadschneider A., PЁoschel T., KЁuhne R., Schreckenberg M., Wolf D.E. -2007. -P. 521-526.
- Hoogendoorn S., van Lint H., Knoop V.L. Macroscopic Modeling Framework Unifying Kinematic Wave Modeling and Three-Phase Traffic Theory//Trans. Res. Rec. -2008. -V. 2088. -P. 102-108.
- Davis L.C. Controlling traffic flow near the transition to the synchronous flow phase//Physica. A. -2006. -V. 368. -P. 541-550.
- Davis L.C. Effect of cooperative merging on the synchronous flow phase of traffic//Physica. A. -2006. -V. 361. -P. 606-618.
- Davis L.C. Effect of adaptive cruise control systems on mixed traffic flow near an on-ramp//Physica. A. -2007. -V. 379. -P. 274-290.
- Jiang R., Hua M.-B., Wang R., Wu Q.-S. Spatiotemporal congested traffic patterns in macroscopic version of the Kerner-Klenov speed adaptation model//Phys. Lett. A. -2007. -V. 365. -P. 6-9.
- Jiang R., Wu Q.-S. Toward an improvement over Kerner-Klenov-Wolf three-phase cellular automaton model//Phys. Rev. E. -2005. -V. 72. -067103.
- Jiang R., Wu Q.-S. Dangerous situations in a synchronized flow model//Physica. A. -2007. -V. 377. -P. 633-640.
- Li X.G., Gao Z.Y., Li K.P., Zhao X.M. Relationship between microscopic dynamics in traffic flow and complexity in networks//Phys. Rev. E. -2007. -V. 76. -016110.
- Pottmeier A., Thiemann C., Schadschneider A., Schreckenberg M. Mechanical Restriction Versus Human Overreaction: Accident Avoidance and Two-Lane Traffic Simulations//Traffic and Granular Flow05. Ed. by Schadschneider A., PЁoschel T., KЁuhne R., Schreckenberg M., Wolf D.E. -Berlin: Springer, 2007. -P. 503-508.
- Siebel F., Mauser W. Synchronized flow and wide moving jams from balanced vehicular traffic//Phys. Rev. E. -2006. -V. 73. -066108.
- Wang R., Jiang R., Wu Q.-S., Liu M. Synchronized flow and phase separations in singlelane mixed traffic flow//Physica. A. -2007. -V. 378. -P. 475-484.
- Kerner B.S., Klenov S.L., Hiller A., Rehborn H. Microscopic features of moving traffic jams//Phys. Rev. E. -2007. -V. 73. -046107.
- Kerner B.S., Klenov S.L., Hiller A. Criterion for traffic phases in single vehicle data and empirical test of a microscopic three-phase traffic theory//J. Phys. A: Math. Gen. -2006. -V. 39. -P. 2001-2020.
- Kerner B.S., Klenov S.L., Hiller A. Empirical test of a microscopic three-phase traffic theory//Non. Dyn. -2007. -V. 49. -P. 525-553.
- Kerner B.S. A theory of traffic congestion at heavy bottlenecks//J. Phys. A: Math. Theor. -2008. -V. 41. -215101-369801.
- Davis L.C. Driver Choice Compared to Controlled Diversion for a Freeway Double On-Ramp in the Framework of Three-Phase Traffic Theory//Physica. A. -2008. -V. 387, -P. 6395-6410.
- Davis L.C. Realizing Wardrop equilibria with real-time traffic information//Physica. A. -2009. -V. 388. -P. 4459-4474.
- Davis L.C. Predicting travel time to limit congestion at a highway bottleneck//Physica. A. -2010. -V. 389. -P. 3588-3599.
- Gao K., Jiang R., Wang B-H., Wu Q.S. Discontinuous transition from free flow to synchronized flow induced by short-range interaction between vehicles in a three-phase traffic flow model//Physica. A. -2009. -V. 388. -P. 3233-3243.
- Wu J.J., Sun H.J., Gao Z.Y. Longrange correlations of density fluctuations in the Kerner-Klenov-Wolf cellular automata three-phase traffic flow model//Phys. Rev. E. -2008. -V. 78. -036103.
- Jia B., Li X.-G., Chen T., Jiang R., Gao Z.-Y. Cellular automaton model with time gap dependent randomisation under Kerners threephase traffic theory//Transportmetrica. -2009. -P. 1944-1987. -DOI: 10. 1080/18128600903312789.
- Tian J-F., Jia B., Li X-G., Jiang R., Zhao X-M., Gao Z-Y. Synchronized traffic flow simulating with cellular automata model//Physica. A. -2009. -V. 388. -P. 4827-4837.
- Kerner B.S., Klenov S.L. Phase transitions in traffic flow on multi-lane roads//Phys. Rev. E. -2009. -V. 80. -056101.
- Kerner B.S., Klenov S.L. A theory of traffic congestion on moving bottlenecks//J. Phys. A: Math. Theor. -2010. -V. 43. -42510.
- Kokubo S., Tanimoto J., Hagishima A. A new cellular automata model including a decelerating damping effect to reproduce Kerners three-phase theory//Physica. A. -2011. -V. 390. -P. 561-568.
- Kerner B.S., Klenov S.L. Microscopic theory of spatial-temporal congested traffic patterns at highway bottlenecks//Phys. Rev. E. -2003. -V. 68. -036130.
- Krauß S., Wagner P., Gawron C. Metastable states in a microscopic model of traffic flow//Phys. Rev. E. -1997. -V. 55. -P. 5597-5602.
- Gipps P.G. A behavioural car-following model for computer simulation//Transportation Research B. -1981. -V. 15. -P. 105-111.


