Теория реальных опционов в оценке последовательных инновационных проектов

По уровню новизны различают два типа инноваций – радикальные (базисные) и улучшающие инновации. Радикальные инновации направлены на освоение новых поколений машин и материалов, принципиально новой техники и технологии, создают такие значительные изменения в процессах, продуктах или услугах, которые приводят к трансформации существующих рынков или отраслей или же создают новые рынки и отрасли. Улучшающие инновации направлены на эволюционное улучшение свойств и параметров процессов, продуктов или услуг, служат распространению и совершенствованию освоенных поколений техники и технологии, созданию новых моделей машин и разновидностей материалов, улучшению параметров производимых товаров, услуг и технологий их изготовления [1]. Отличительной особенностью большинства инновационных проектов является постоянное улучшение инновационного продукта (т. е. улучшающие инновации), что позволяет выделить отдельные поколения развития технологии. Во многих проектах инновационный продукт одного поколения рассматривается как платформа (база) для будущего поколения инновационных продуктов. Предлагается подход к оценке инновационных проектов, для которых рынок сбыта ограничен (т. е. спрос задается определенными рамками, что характерно для ряда инновационных отраслей) и существует конкуренция. Наличие конкуренции является важным фактором, так как именно конкуренция заставляет производителя постоянно выводить инновационные продукты на рынок.

Предположим, что существует компания, которая через одинаковые промежутки времени t планирует запускать на рынок инновационные продукты P_t = 1, …, T , где T – время жизни технологии. При этом каждый из последующих продуктов P_{t + 1} является усовершенствованием предыдущего P_t , и с началом производства продукта нового поколения P _{t + 1} производство продукта предыдущего поколения P_t прекращается. Первоначальные инвестиционные затраты на выпуск каждого продукта P_t составляют I_{t – 1}, а чистый поток от реализации одного продукта составляет C_t . Одним из основных факторов неопределенности для компании является спрос на продукцию в каждом из периодов x_t , при этом известно, что спрос при благоприятном стечении обстоятельств составляет x_t ⁺ , при негативном развитии событий – x_t . В первом периоде вероятность высокого спроса составляет q ₁, вероятность низкого – (1 – q ₁). Для последующих периодов действуют следующие условия:

– если спрос на продукт P_t был высоким, то вероятность высокого спроса и на продукт P_{t + 1} составляет q_{t +}, и с вероятностью (1 – q_{t +}) он будет низким.

– если спрос на продукт P_t был низким, то вероятность высокого спроса для продукта P_{t + 1} составляет q_{t –}, и с вероятностью (1 – q_{t –}) он будет низким.

На основе вышеизложенных данных можно построить следующее дерево потоков (рис. 1).

Согласно методу NPV , для определения целесообразности реализации проекта необходимо определить денежные потоки для каждого из периодов с учетом вероятностей, например ожидаемый денежный поток периода 2

f > = q 1 ⁽ q + ' ⁽ c 2 ' x + - I 2 ) ⁺ (1 - q 2 ) ' ⁽ c 2 ' x 2 - I 2 )) ⁺ (1)

^{+ (1} - q 1 ) ■ ( q 2 ■ ⁽ c 2 ■ x 2 - I 2 ) ^{+ (1} - q 2 ) ■ ⁽ c 2 ■ x 2 - I 2 ⁾⁾-

После этого каждый из ожидаемых денежных потоков f необходимо привести к начальному периоду времени по ставке дисконтирования к (при этом к задается извне как ожидаемая норма доходности по альтернативным вложениям)- Формула NPV выглядит следующим образом:

Tf

NPV = У — f t —-           (2)

1: 0 (1 + к ) -                    ⁽⁾

Проект принимается, если NPV > 0 и отклоняется, если NPV < 0-

Вместе с тем главный недостаток метода NPV заключа-ется в том, что он не учитывает возможность руководства проекта в ходе его реализации проекта вносить изменения, например, расширить или сократить производственные мощности, приостановить проект с последующим возобновлением деятельности, прекратить осуществление проекта и пр- Реализация этих мер положительным образом влияет на NPV и снижает риск проекта- Для проектов, предусматривающих постоянное обновление, к управленческим решениям могут относиться меры по выбору оптимального момента времени для вывода нового продукта на рынок, переключение между разными технологиями и пр- [2; 3; 4]- Стратегическая чистая приведенная стоимость проекта NPV состоит из двух слагаемых:

• 1)    чистая приведенная стоимость проекта без учета возможностей внесения изменений ( NPV );

• 2)    стоимость опционов проекта ROV .

Формула для стратегического (расширенного) чистого приведенного значения выглядит следующим образом:

NPV * = NPV + ROV -           (3)

Рассмотрим возможность прекращения проекта на примере дерева принятия решений (рис- 1)- Анализ дерева принятия решений необходимо начинать с конца дерева. Имеет смысл отказаться от реализации проекта, если приведенные потоки денежных средств меньше, чем ин- вестиционные затраты, т- е-

I. - 1

< q . ■ xt ^{+ (1 -} q . ) ■ x t 1 + к

Данную проверку необходимо осуществить в каждом из узлов дерева принятия решения, двигаясь справа налево с конца дерева (периода T) до его начала- В каждом узле при этом необходимо суммировать денежные пото- ки периода и приведенные к этому периоду значения будущих потоков- Дерево потоков трансформируется в следующее дерево ценности (рис- 2)-

В результате проведенного анализа, экономические неэффективные ветки дерева будут урезаны, что приводит к модифицированному дереву потоков, например, следующего вида (рис- 3),

Согласно методу дерева принятия решений DTA , для модифицированного дерева потоков составляются ожидаемые денежные потоки f' , которые затем дисконтируются к начальному моменту времени по ставке к - То есть:

NPV

DTA

T f .' 1 :0 (1 + к ) -’

при этом NPV_DTA >  NPV -

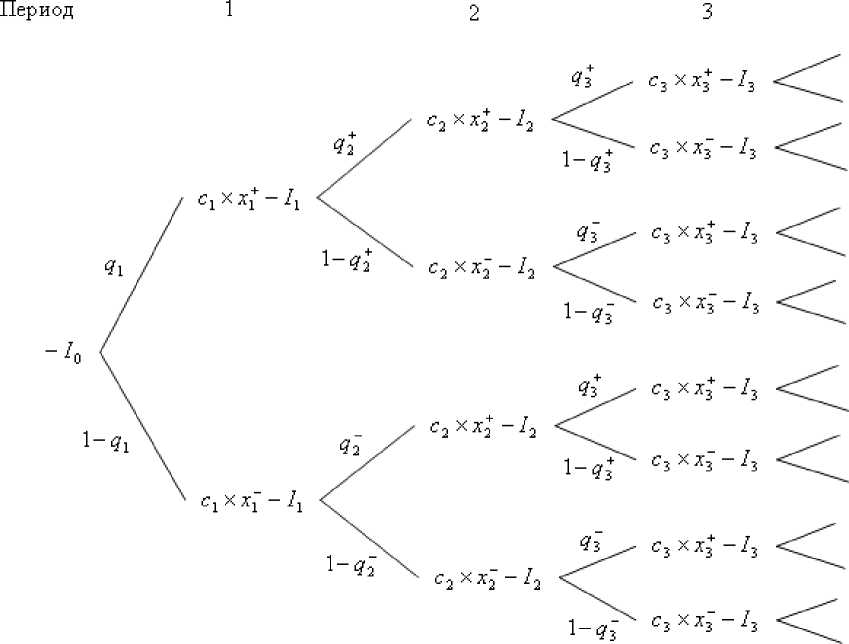
Рис- 1 - Дерево потоков для последовательных инновационных проектов

Недостатком метода дерева принятия решений DTA является то, что он не дает никаких указаний по корректировке ставки дисконтирования проекта в связи с уменьшением риска за счет исключения из расчета неэффективных сценариев развития. Для решения данной проблемы можно воспользоваться методом реальных опционов ROA , который позволяет не только учесть возможность принятия гибких управленческих решений, но и скорректировать ставку в соответствии с теорией финансовых опционов [3; 4].

Рассмотрим следующий числовой пример. Компания планирует вывести на рынок два последовательных продукта P ₁ и P ₂. Инвестиционные затраты на запуск продукта P ₁ составляют 1000 у. е., на запуск продукта P ₂ – 2000 у. е. При благоприятном спросе денежные потоки продукта

P ₁ составят 700 у. е., при неблагоприятном 300 у. е., для продукта P ₂ – 5 500 у. е. и 2 000 у. е. соответственно. Вероятность благоприятного спроса для продукта P ₁ составляет 50 %, неблагоприятного 100 – 50 = 50 %. Вероятность спроса на продукт P ₂ зависит от спроса на продукт P ₁. Если спрос на продукт P ₁ был высоким, то вероятность высокого спроса на продукт P ₂ составляет 80 % (вероятность низкого спроса 100 – 80 = 20 %). Если спрос на продукт P ₁ был низким, то вероятность высокого спроса на продукт P ₂ составляет 30 % (вероятность низкого спроса 100 – 30 = 70 %). Ставка дисконтирования для проектов данной отрасли k составляет 30 %, безрисковая ставка r составляет 10 %. Дерево потоков проекта можно представить в следующем виде (рис. 4).

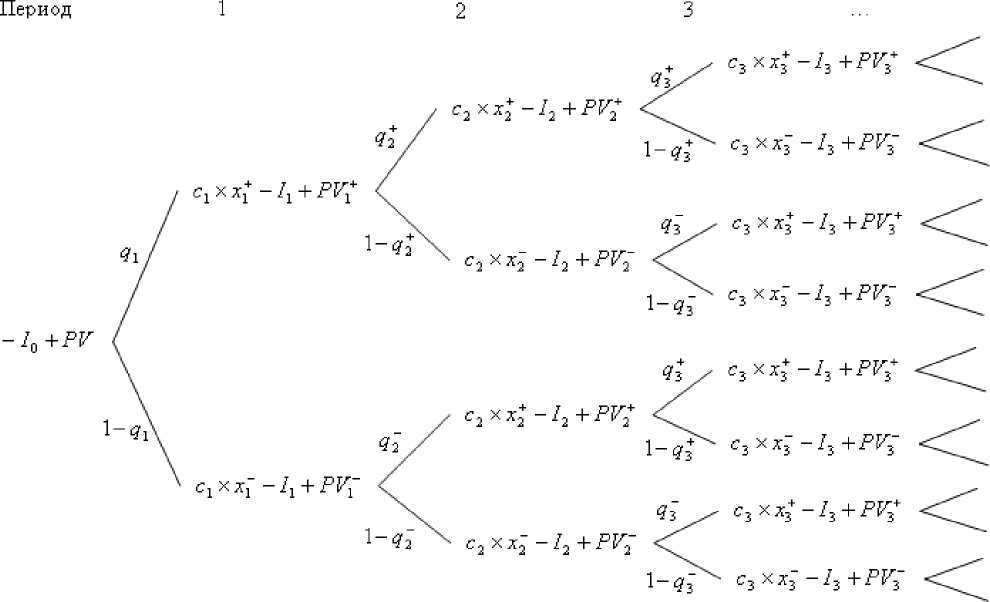
Рис. 2. Дерево ценности для последовательных инновационных проектов

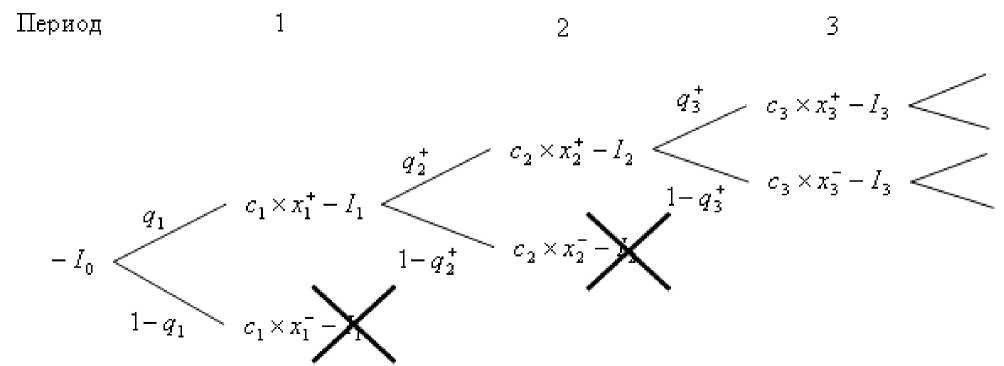
Рис. 3. Модифицированное дерево потоков для последовательных инновационных проектов

Оценивая проект с помощью критерия NPV , можно прийти к выводу, что проект неэффективный:

NPV = - 1 000 ±                     ±

1 ± ^0,3

± 0,5 ■ (0,8 ■ 5 500 ± 0,2 - 1 000) ± 0,5 ■ (0,3 ■ 5 500 ± 0,7 - 1 000) _ - 98 ⁽⁶⁾

±                             (1 ± 0,3)²                              =

Для учета возможности прекращения проекта построим дерево ценности (рис. 5).

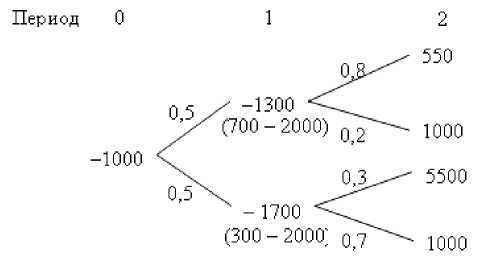
Рис. 4. Дерево потоков для компании

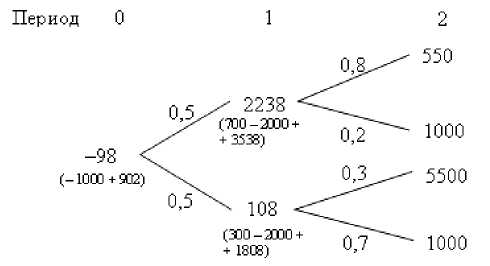
Рис. 5. Дерево ценности для компании

Анализируя дерево ценности можно сделать вывод, что при низком спросе на продукт P 1 инвестировать в продукт P ₂ неэффективно, так как чистая приведенная стоимость такого проекта отрицательная ( NPV 1 ^- = -I 1 + PV , " = -2 000 + 1 808 = -192 у е.). Модифицированное дерево потоков с учетом прекращения проекта при низком спросе на продукт P 1 будет выглядеть следующим образом (рис. 6).

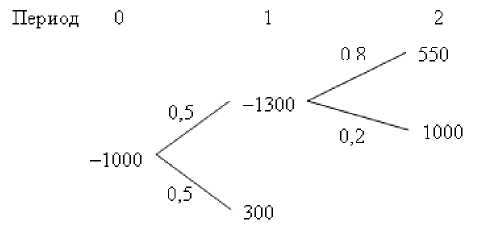
Рис. 6. Модифицированное дерево потоков для компании

Чистая приведенная стоимость по методу дерева принятия решений ( DTA ) составит

NPV_dta = - 1000 ± 0,5 ■ ( - 1300) ± 0,5 ■ 300

±         1 ± 0,3

0,5 ■ (0,8 ■ 5500 ± 0,2 ^ 1000) (1 ± 0,3)²

±

_ - 24 у. е.

Стоимость опциона в этом случае составляет

ROV dta = -24 - (-98) = 74 у е.         (8)

Вместе с тем, несмотря на то, что риск проекта был снижен за счет уменьшения разброса приведенных значений, ставка дисконтирования осталась неизменной. Чтобы откорректировать ставку дисконтирования, необходимо воспользоваться теорией реальных опционов и риск-нейтральным подходом. Риск-нейтральный подход предполагает определение риск-нейтральных вероятностей для потоков проекта, для того чтобы появляющуюся в результате управленческой гибкости дополнительную ценность проекта (так как эта ценность не несет в себе дополнительного риска) можно было дисконтировать по безрисковой ставке. На рис. 7 видно, что приведенная стоимость потоков в период 0 составляет 902 ( 5 = 902) и получается взвешиванием стоимости проекта в период 1 по фактическим вероятностям в случае благоприятного ( 5 ^ = 2 238) и неблагоприятного ( S = 108) развития событий и дисконтированием полученного результата по ставке 30 %.

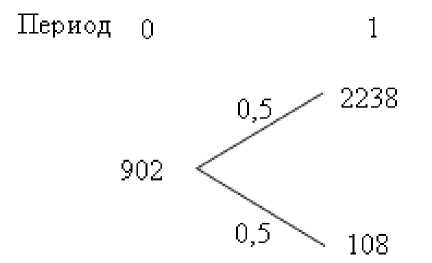
Рис. 7. Приведенные стоимости проекта при фактических вероятностях

Риск-нейтральные вероятности рассчитываются по следующим формулам:

1 ± r - d p _ — u - d

где u = S / 5 , d = S ' / S .

В приведенном выше примере и = 2 238/902 = 2,48; d = 108/902 = 0,119; p =(1 + 0,1 - 0,119)/(2,48 - 0,119) = 0,415, или 41,5 %.

Таким образом, приведенная стоимость проекта при риск-нейтральных вероятностях будет выглядеть следующим образом (рис. 8).

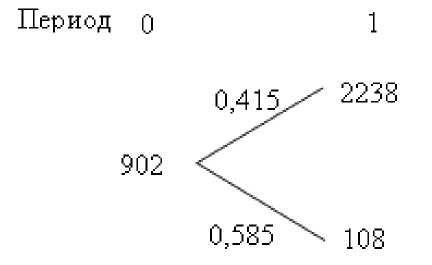
Рис. 8. Приведенная стоимость проекта при риск-нейтральных вероятностях

Стоимость опциона на прекращение проекта приведена на рис. 9.

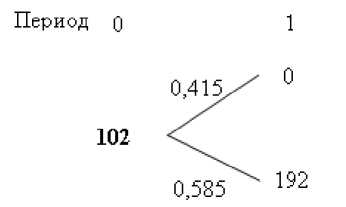
Рис. 9. Стоимость реального опциона на прекращение проекта

Таким образом, NPV_ROA = NPV + ROV_ROA = –98 + 102 = 4 у. е.

Сравнение результатов оценки последовательных инновационных проектов приводится в таблице ниже.

Таким образом, классический критерий оценки инвестиционных проектов NPV свидетельствует о том, что проект экономически неэффективен. Вместе с тем в проекте заложена возможность отказа от продолжения выпуска продукта P2 в случае низкого спроса на продукт P1. Существует два способа оценки данной возможности прекращения проекта (реального опциона на отказ): метод дерева принятия решений и метод реальных опционов. Метод дерева принятия решений занижает стоимость опциона, так как не учитывает изменение риска проекта. Дисконтирование потоков проекта производится по стоимости капитала проекта k = 30 %. Приведенная стоимость опциона в этом случае составляет 74 у. е., а расширенное NPV равно –24 у. е. Метод реальных опционов учитывает уменьшение риска проекта путем использования риск-нейтральных вероятностей и дисконтирования по безрисковой ставке процента r = 10 %. Определенная в соответствии с методом реальных опционов стоимость опциона на отказ составляет 102 у. е. и приводит к тому, что стратегическая чистая приведенная стоимость проекта становится положительной (NPV = 4 у. е.) и, следовательно, проект можно рекомендовать к реализации.