Теплофизический расчет взаимодействия металлизованных окатышей и жидкой лигатуры при получении цельнолитой заготовки для ЭШП

Одним из способов снижения себестоимости электрошлакового металла является формирование расходуемого электрода из смеси металлизованных окатышей (МО) и жидкой лигатуры [1]. Полученная смесь лигатура - МО подается в специальную изложницу, где происходит ее кристаллизация и получение цельнолитой заготовки для электрошлакового переплава (ЭШП).

При осуществлении данного способа формирования заготовки возникает ряд технологических проблем. Прежде всего, необходимо определить соотношение расплав - металлизованные окатыши. С одной стороны, чем больше в составе смеси МО, тем меньше себестоимость электрода, с другой стороны, окатыши как охладитель снизят температуру смеси и монолитного формирования заготовки не произойдет. Также возникает вопрос, с какой начальной температурой подавать составляющие смеси расплав - МО. Ответ на эти вопросы можно получить с помощью математической модели, описывающей теплообмен между компонентами смеси.

В работе [2] рассмотрены теплофизические процессы в элементарной ячейке «расплав - ме-таллизованный окатыш», где получены значимые характеристики по динамике изменения радиуса окатыша, коэффициента теплообмена между расплавом и окатышем.

В данной работе рассматривается теплообмен между составляющими смеси расплав - МО. При постановке задачи были приняты следующие, достаточно общие, допущения:

• 1.    Теплообмен с окружающей средой отсутствует.

• 2.    Теплопередача между составляющими смеси осуществляется по закону Фурье и значительно превосходит теплопередачу теплопроводностью ввиду малого времени «существования» смеси.

• 3.    Компоненты смеси полностью перемешиваются между собой, т.е. принята модель идеального смешивания.

• 4.    При достижении температуры ликвидуса расплава полагаем, что смесь закристаллизовалась.

С учетом принятых допущений уравнения, описывающие теплообмен между компонентами смеси, имеют вид [3]

— = ле,                           (1)

dT

где 0Г (т) = (0] (т)02 (т)) - вектор-функция температур компонентов смеси;

(-нх нх)

А = \           - матрица параметров физи ческих свойств компонентов смеси.

Начальные условия: 07 (0) = (01ОО2о)-

В уравнении (1) приняты обозначения 0, -температуры компонентов z-й смеси; т - время, с; Н, = aF /(руС^); а - коэффициент теплопередачи, Вт/(м²*°С); F - поверхность раздела смесеобразующих компонентов, м²; р^с^У, - соответственно плотность, кг/м³; удельная теплоемкость, Дж/(кг-°С); объем м³ z-й компоненты смеси; z = 1 для расплава, z = 2 для МО.

После преобразования по Лапласу системы (1) и решения ее получим

• (5 ) = (s0_w +0_]О^2 +O₂o^i)/s(^ + ^i +^2); 7’2М = (^_2О+0_1О^₂+02О^₁)/^(^ + Я₁+Я₂), ⁽

где T^s) - изображения по Лапласу функций 0_Z (t),(z = 1,2) ; 5 - комплексный параметр оператора Лапласа. После обратного перехода от изображения к оригиналу, получим решение системы (1) в виде

0! (т) = 010^2 ⁺ Г®20 + ^ ^ (610 “ 620 )"1 Р\ >

02 (Т) = 620 А + [б10 -е (Ою ~ 020 )] Р2 ’ где Ъ = НХ+Н2\ Р\ = Нх !Ь; р2 =Н2 / b.

Для расчета параметров системы (1) была проведена серия экспериментов. Так, для определения поверхности раздела сред F вычислялось число МО -ив объеме У₂ по экспериментально определенной 8 пористости засыпки. Величина ^Е(^мо) равна:

8 = (г2-л4оИ/б)/К2                 (4)

и представляет собой долю пространства засыпки объема У₂, незаполненную МО, причем 0 < s < 1. Как известно, средний диаметр металлизованных окатышей составляет от 5 до 25 мм. Поэтому эксперименты проводились для МО с диаметрами в этом интервале. Засыпка МО осуществлялась произвольно без уплотнения, вибрации, т.е. так, как формируется в производственных условиях. Окатыши перед засыпкой замачивались в воде, так как они пористые и часть воды поглощают. Засыпка из МО объема У₂ заливалась водой до определенного уровня. Затем вода выливалась, и измерялся ее объем. Все экспериментальные данные статистически обрабатывались со всеми оценками погрешностей. В результате была получена зависимость пористости засыпки МО от диаметра окатышей в виде

Е(4ю) = -1,347-10-3^о +

+0,055^МО + 0,018,                      (5)

где d_MO - диаметр металлизованных окатышей, мм.

Коэффициент погрешности при вычислении s (dMO) не превышает 0,037. Как видно из уравнения (5), величина пористости засыпки нелинейно зависит от диаметра окатышей: max 8 (20,41) = 0,579.

По известной пористости засыпки и данного диаметра МО определяется их число и по формуле (4) в объеме У₂:

_И = ((Г₂-Г₂8)6)/л4_о.                (6)

Суммарная площадь теплообмена между расплавом и металлизованными окатышами равна:

^F = п^мо •                           (7)

При этом реальная площадь теплообмена будет несколько меньше, так как окатыши будут иметь точки касания друг с другом, но это будет зависеть от соотношения объемов У_х и У₂. Чем больше У_х точек касания между МО будет меньше, и погрешность в определении F соответственно меньше. Для расчета температурных характеристик компонентов смеси был составлен алгоритм и разработана программа расчета на компьютере.

Массив исходных данных для одного из вариантов расчетов представлен в таблице.

Исходные данные для расчета

Параметр	Размерность	Расплав, z = l	МО, / = 2
0	°C	01О =1600	02о = 200
а	Вт/(м°С)	35 000	35 000
Р	кг/м3	7790	2600
с	Дж/(кг-°С)	840	487,9
У	м3	0,25	0,1
^мо	м	-	0,02
8	-	-	0,5792

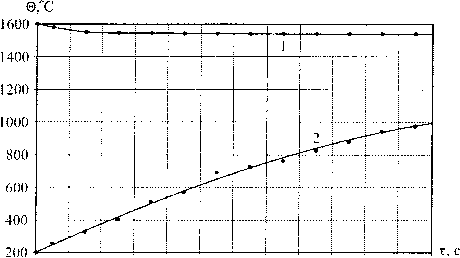
Зависимости температуры компонентов смеси «расплав - МО» по времени представлены на рис. 1.

0 0,02 0,04 0,06 0,08 0,10 0,12 0/14 0J6 0.18 0.20 0,22 0,24

Рис. 1. Изменение температуры компонентов с течением времени: 1 - расплав, 2 - металлизованные окатыши

Ворона Е.А., Потапов В.И., Суров А.Н., Нуманов И.В.

Теплофизический расчет взаимодействия металлизованных окатышей и жидкой лигатуры...

Зависимость времени «схватывания» смеси т^ от соотношения объемов компонентов смеси (расплав / МО) У₂ / ¥_х представлена на рис. 2.

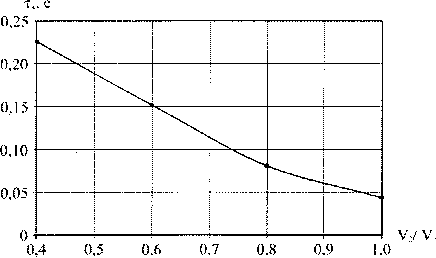
Рис. 2. Изменение времени кристаллизации смеси т^ в зависимости от ¥2 / ¥х

При изменении начальной температуры окатышей 6₂₀ время кристаллизации смеси х_к представлено на рис. 3.

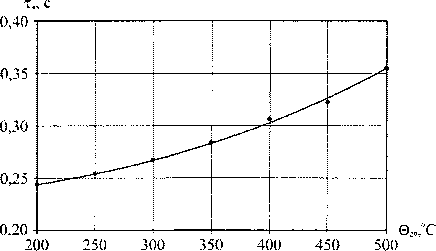
Рис. 3. Изменение времени кристаллизации смеси х_к в зависимости от начальной температуры окатышей 6₂₀

Выводы

Получены зависимости температуры жидкой лигатуры, начальной температуры подогрева металлизованных окатышей и их соотношений объемов в смеси от времени. По формуле (3) можно рассчитывать время кристаллизации смеси, что позволит определить время транспортировки смеси к изложнице для формирования цельнолитой заготовки в условиях промышленного производства.

Работа выполнена при финансовой поддержке в рамках проекта № 2.1.2/207 «Развитие научного потенциала высшей школы (2009-2010 гг.)»