Тепло- и массообмен в области с движущимися границами

В работе [1] содержится обзор задач о переносе тепла теплопроводностью в области с движущейся границей. Математические модели этих процессов включают в себя уравнение теплопроводности в декартовой или цилиндрической системах координат, условия перемещения границ области, начальное и граничные условия.

В дальнейшем круг расчёта тепло- и массообмена в областях с перемещающимися границами расширился и теплопроводность стала их частью. Можно выделить следующие задачи.

• 1.    Расчёт переходных процессов в обогреваемых каналах с кипящим теплоносителем в ядерных реакторах и паровых котлах [2–19].

• 2.    Процессы внутренней баллистики в камере сгорания с зарядами торцевого горения [20].

• 3.    Внутренняя баллистика низкотемпературных газогенераторов с твёрдым охладителем [21–24].

Математические модели данных задач достаточно сложны, что не позволяет получить аналитические решения в практически важных случаях. Основным методом решения таких задач становится прямое численное интегрирование уравнений математических моделей.

В обогреваемом канале можно выделить три характерных участка, отличающихся состоянием теплоносителя (рис. 1).

q

И ^М М^М + _^

• ¹    1 1               2 l ₂            3 l z

Рис. 1. Схема обогреваемого канала: 1 – участок без кипения,

• ¹    ; 2 – участок поверхностного кипения, ^{1       2} ;

• 3    – участок объёмного кипения, ²

В переходных процессах, вызванных изменением граничных условий и величины теплового потока q , положение границ участков меняется.

В камере сгорания с зарядом твёрдого топлива, горящего с торца, с течением времени увеличивается пространство между торцом заряда и критическим сечением (рис. 2).

l

l

Рис. 2. Схема камеры сгорания: 1 – заряд топлива        ¹ ;

z

2 – канал камеры сгорания, ¹

В камере охлаждения низкотемпературного газогенератора можно выделить область с гранулами охладителя и область, свободную от гранул (рис. 3). По мере разложения охладителя под действием газового потока гранулы перемещаются в направлении течения.

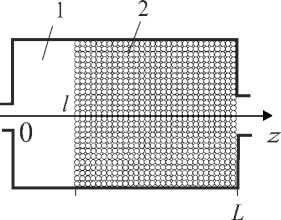
Рис. 3. Схема камеры охлаждения:

1 – свободная от гранул область,        ;

2 – область с гранулами, ^≤≤

Во многих практически важных случаях для расчёта нестационарных режимов работы применяются одномерные математические модели, которые включают в себя дифференциальные уравнения в частных производных неразрывности, импульса и энергии для рабочего тела. Дополнительно в математические модели могут включаться уравнения теплопроводности для стенки канала, заряда твёрдого топлива, гранулы охладителя, уравнения неразрывности компонентов, из которых состоит рабочее тело, например, уравнение генерации пара в обогреваемом канале, уравнения неразрывности компонентов продуктов сгорания топ- лива и т. п.

Для решения системы уравнений широко применяется метод конечных разностей с использованием фиксированной разностной сетки [25]. Однако в этом случае положение границ между участками можно определить с точностью до шага сетки. В целом ряде случаев для обеспечения нужной точности требуется применять сетки с мелким шагом и интерполяцию.

В работах [1, 26] рассмотрено применение координат, связанных с границей области интегрирования. Применение такого преобразования позволяет точно отслеживать положение границ области.

Запишем систему уравнений неразрывности, импульса и энергии в векторной форме дФ д¥

1 дт д z

где в случае течения жидкости или газа

Ф =

PS

G

G

V = Gw + pS

p eS

Ge + pwS

J m

„ p w ² П

^—^ ■ J imp ^- g P sin Y

П w q w ⁺ J e

а в случае течения кипящего теплоносителя

PS

Ф = G

x S

V =

G

G ²

v ⁺ P^S

S p ₂

Gh

X = ( 1 -ф ) p' h '+ ФP" h ''- p ;

G 2 П

-^ ^2" - g ^P sin ^Y

8 S P

П _wq_w

±=IMl+xt

P 2 ( 1 -ф ) p ' фp "'

Уравнение неразрывности i -го компонента рабочего тела можно представить в виде

dPSgi , д Ggi дт + дz " J

Расчет и конструирование

В области, занятой гранулами охладителя S = S 0 s, где S 0 - площадь сечения пустой камеры

охлаждения, а s - пористость.

В (1)...(4) G – расход; р – давление; w – скорость; S – площадь сечения; e – внутренняя энергия; h - энтальпия; р - плотность; т - время; z - координата; П - периметр сечения; g - ускорение свободного падения; у - угол между осью канала и горизонталью; q - плотность теплового потока; ^ - коэффициент гидравлического сопротивления; ф - истинное объёмное паросодер-

жание; x – массовое паросодержание; J_m – поток массы; J_imp – поток импульса; J_e – поток энер-

гии; J_i – источник массы i -го компонента; g_i – массовая доля данного компонента; индексы ' и '' обозначают параметры жидкости и пара на линии насыщения.

В области / 1 ( т ) < z <  I 2 ( т ) введём координату у следующим образом [26]

z - к ( т )

у =---1^—

1 2 ( Т ) - l i ( T )

.

Система уравнений (1) преобразуется к дивергентному виду дА1Ф  д Г,  Г/,   ddk    dk Ъ!,

-----+ — ^Т- ( 1 - у ) —¹ + у Ф J = А 1F , А 1 = 1 2 - 1 1 .

дт    д у [    L       d Т т      d т _|

Уравнение (4) приводится к виду дА 1 р Sg=  д U   Гл   ddkdL

---i-^- + — Gg: - ( 1 - у )    + у -2- р Sg: = А и, .

дт      ду [ i v     ' dт      dт

В области 0 <  у <  1 строится равномерная разностная сетка с шагом 1/ ( N - 1 ) , где N - число

узлов сетки. При изменении границ области 1 1 ( т ) , 1 2 ( т ) изменяются z -координаты узлов сетки,

а y -координаты остаются постоянными.

Уравнение (6) аппроксимируется неявной разностной схемой

Ф m ^{+ 1} А 1 m ^{+ 1} - Ф m А 1 m 0 m ^{+ 1} - 0 m + ¹ n                    n I n n 1

Ат             А у

= А 1 m ^{+ 1} F m ^{+ 1}

0 = Т- ( 1 - у ) — + у—- 2- Ф . ^v ’ d т d т

Векторы Ф, Т , F нелинейны относительно вектора неизвестных Y = G , Т , р^ или Y = G , h , р^ . Разложим векторы Ф m ^{+ 1}, Т m ^{+ 1}, F nm ^{+ 1} в ряд Тейлора с сохранением первого члена ряда. Получим двухточечное разностное уравнение

A n Y nm ^{+ 1} - B n V ' = C n , (10) где

A n

= А 1^{m + 1}

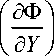
m + 1

n

^А у

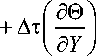
m + 1

n

Г     ^{m + 1}

-АтА у А 1^{m + 1} 1--| ; B_№ \ OI /

n

P®

= АтА у I--- (д Y

____ ____

C n = Ф m А 1^m А у - Ф m ^{+ 1} А 1^{m + 1} А у - Ат 0 m ^{+ 1} - 0 m + + АтА у А 1^{m + 1} F n ^{m + 1} + A n Y nm ^{+ 1} - B „ - 1 Y „^m + 1

В (11) индекс m +1 обозначает значение параметра на предыдущей итерации ( m +1 ) -го слоя по времени. В (9) A n , B_n - 1 - квадратные матрицы размерности 3 х 3, C_n - векторы размерности 3.

Граничные условия для задач 1…3 записываются следующим образом.

Задача 1:

Р ⁽0, т⁾ = Р 1 ⁽т⁾-А р 1 ;     h ⁽0, т⁾ = h ₁⁽т⁾; р ⁽ 1 , т⁾ = p_t ⁽т⁾ + А р , .                                       (12)

Задача 2:

G ( 0, т ) = и т Р т F ;     T ( 0, т ) = Т_гор ;    G(1 , т ) = G _кр.                                                 (13)

Задача 3:

т k ^{p (т} ,^{0 )} ₊ ^{G 2 (}т ,2). к - 1 ^{кс кс (} ) к - 1 р ( т )      2 S ² Р ;

G ²

p-с(т)=p,г0,, pH ,<)S (т-0);

G ( т , l ) =Ц S в _Ы х

2 k

;—г Р Р

2 k

I

I pJ

f > ( к + 1)/ к "

p1-1I p J

.

В (11)...(14) A p - местные потери давления; R - газовая постоянная; к - отношение теплоёмкостей; ц - коэффициент расхода; и _т - скорость горения; F - площадь горения; S _вых - площадь выходного патрубка; индексы кс – камера сгорания; т – топливо; н – наружная среда.

Таким образом, граничные условия для задач 1–3 можно записать в обобщённой форме.

При z = 0

f . ( p , t , w ) _z = 0

При z = l fi(p, t, w)z=l

Положение tw = ts +At, где

= 0; f 2 ⁽ p , t , w ) _z = o = 0.

= 0.

границы начала участка поверхностного кипения определяется из условия t_w и t_s температура стенки и температура насыщения соответственно, а начало

участка объёмного кипения определяется из условия h = h . Температура стенки определяется из решения уравнения теплопроводности дA lt дт

( 1 - y ) dr + ydl ² d т     а т

1 a _, д² 1 . , д²1 a„ ,A l д t q, ,A l t ^ =—— t + a w AI—g + - w + —

A l д у ²        д г ²     r д r p _wc_w

с граничными условиями третьего рода на боковых поверхностях трубы и адиабатными условиями на торцах трубы. В (17) q_v – плотность внутренних источников тепловыделения, индекс w означает параметры стенки.

Положение поверхности горения заряда топлива в задаче 2 определяется из уравнения dl

— =-u т ат с начальным условием l(0) = l0.

Положение границы области с гранулами определяется из следующих соображений. При обтекании потоком газа гранул охладителя они уменьшаются в размерах и смещаются в сторону движения газа таким образом, что пористость слоя остаётся постоянной и равной начальной.

В разностной аппроксимации граничные условия (15) запишем в виде

AY^{m + 1} = C 1 ,

где A 1 - прямоугольная матрица размерности 2 x 3, а С 1 - вектор размерности 2.

A =

д f ,	д f 1	д f 1
д G	д p	д t
д f 2	д f 2	д f 2
д G	д p	д t

;

m + 1

C =

дf    дA    af g + 'I p + 'I t д G    дp д t f G +f p +f t д G    дp    д t

m + 1

f 1

f 2

m + 1

.

Граничные условия (16) в разностной форме запишем в виде о у m +1 _ /*» B N Y N = C N ,

где B_N - матрица 1 x 3, C_N - скаляр.

B

' N =

= f

д G

д f N д f N д p д t

_ m + 1

;

N

_г _ д f N C N =

N G G ^д p +дц д G     д p     д t

_ m + 1

m + 1

^— f N .

N

Расчет и конструирование

Для решения краевой задачи (10), (19), (20) применяется метод ортогональной прогонки [27].

Уравнение теплопроводности (17) решается методом продольно-поперечной прогонки [27].

Уравнение (7) аппроксимируется неявной разностной схемой m+1 m+1         m m               m+1 „m+1               m+1 „m+1

(PSg)n Al     (PSg)n Al , (G -XPS)n gn -(G -XPS)n-1 g„-1 _At                           h

= A i m + 1 J m + 1 , X = ( 1- y ) ^ + ydl 2 , d T     d T

откуда определяется массовая доля i -го компонента

g

m + 1

n

m + 1

_ b n - 1 g n - 1

+ C

n

a

n

m + 1                                m + 1                                 m + 1 .

a n ^_(P S ) n ^{A l} h ^{+ AT} G ^-XP S ) n ; b n - 1 ^_AT G ^-XP S ) n - 1 ;

mm           m mm       m + 1 m + 1

cn = (PSg ) n hAl - y(G - XPS ) n gn + At hAl Jn .

На рис. 4 представлены результаты расчёта переходного процесса в парогенерирующем канале при скачкообразном увеличении теплового потока на 21 % от стационарного состояния, а на рис. 5 представлены результаты расчёта переходного процесса при скачкообразном уменьшении энтальпии на входе в канал на 26 % от стационарного состояния.

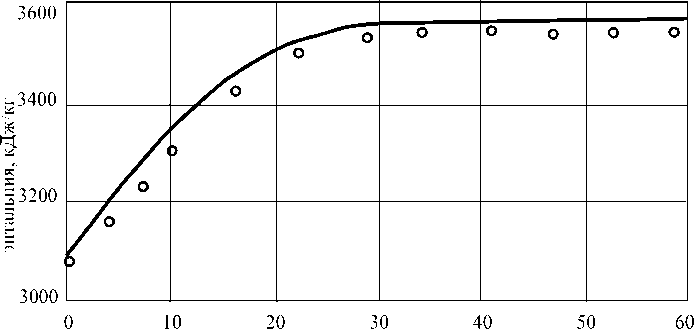
время, c

Рис. 4. Изменение энтальпии на выходе из канала при увеличении обогрева

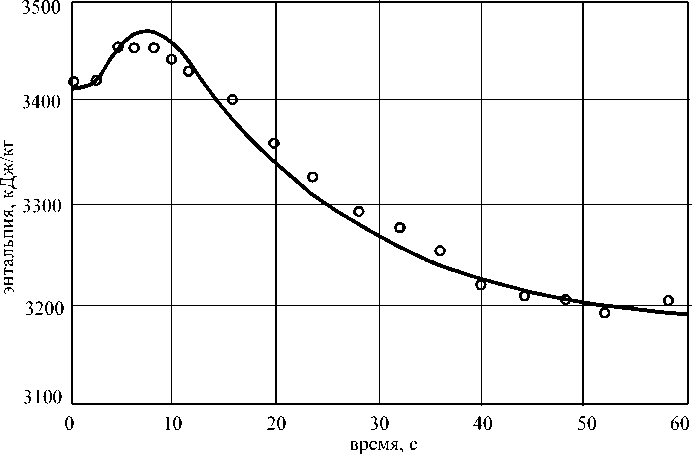
Рис. 5. Изменение энтальпии на выходе из канала при уменьшении энтальпии теплоносителя на входе

На рис. 6, 7 представлены результаты расчёта низкотемпературного газогенератора с твёрдым охладителем.

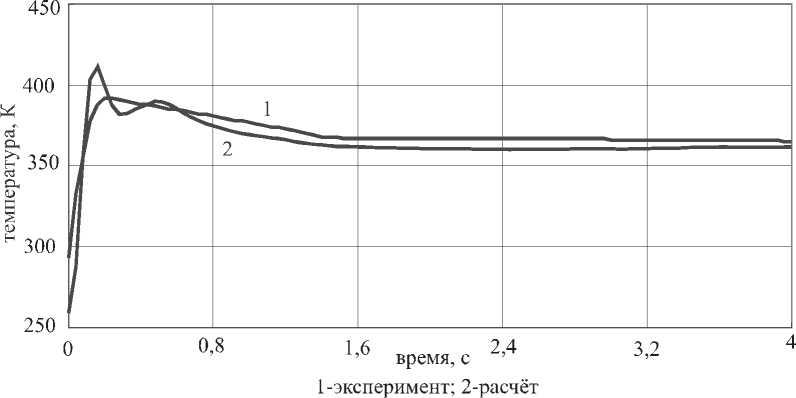
Рис. 6. Изменение температуры на выходе из газогенератора

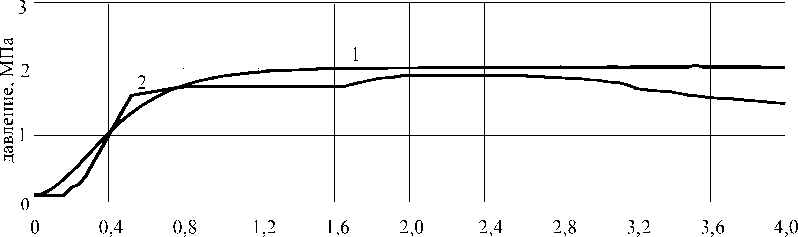
время, с

1- эксперимент; 2 - расчет

Рис. 7. Изменение давления на выходе из газогенератора

Выводы

• 1.    Предложенный метод расчёта нестационарных режимов тепло- и массообмена позволяет точно определять положение границ расчётных областей.

• 2.    Метод обладает высокой вычислительной эффективностью. Применение неявных разностных схем позволяет существенно сократить затраты машинного времени.