Теплоотдача в поле центробежных сил для элементов газовых турбин

Введение. Учет особенностей теплоотдачи в проточных частях турбонасосных агрегатов (ТНА) жидкостных ракетных двигателей (ЖРД) является актуальной задачей. В настоящее время учет особенностей течения с теплоотдачей при реализации потенциального и вихревого вращательного течения в проточных частях в основном осуществляется следующими методами: использованием эмпирических уравнений, численными и аналитическими методами решения дифференциальных уравнений в частных производных [1].

Первый метод не всегда обеспечивает требуемую точность расчета гидродинамических и тепловых характеристик вращательных течений с учетом теплоотдачи и требует дополнительных уточняющих экспериментальных исследований. Как правило это влечет достаточно большие временных и материальных затрат на постановку и проведение исследований.

Численные методы достаточно сложны в использовании при проведении инженерных расчетов и требуют реализации их в специализированном программном обеспечении. Численные методы исследования используют прямое численное моделирование (метод DNS) и усредненные уравнения Навье-Стокса и Рейнольдса (RANS метод). Выбор метода зависит от сложности проблемы и точности результатов. Достаточно часто используется метод RANS с использование моделей k-ε и k-ω турбулентности [2–7]. Вопросы теплоотдачи при обтекании криволинейной поверхности с продольной кривезной газообразным потоком рабочего тела так же рассмотрены в работах [8–10], где исследованы случаи обтекания лопаток турбин. В работе [11] исследуется конвективный теплообмен в канале с периодическими выступами на основе многоблочных вычислительных технологий, основанных на решении факторизованным конечно-объёмным методом уравнений Рейнольдса, замыкаемых с помощью модели переноса сдвиговых напряжений Ментера, и уравнения энергии на разномасштабных пересекающихся структурированных сетках.

Аналитический метод позволяет получить аналитические зависимости применимые для инженерных расчетов в широком диапазоне возможных вариаций конструктивных и режимно-эксплуатационных параметров. Аналитические методы, как правило разрабатывались для прямолинейного равномерного течения и имеет ряд ограничений. Одно из ранних исследований это работа Е. Л. Кнута [12], в которой анализ основан на расшириной аналогии Рейнольдса с передачей тепла, массы и импульса в развитом турбулентном потоке в трубе. Использование профиля распределения скорости и температуры в пограничном слое предложено В. Д. Ранни [13] и модифицировано Д.Л. Туркоттом [14]. Анализ подслоя, проведенный Туркоттом, учитывал влияние теплообмена на турбулентность. Аналитичекие методы определения коэффициентов теплоотдачи предложенные в работах [15; 16] учитывает конвективный перенос тепла в камерах ЖРД и выполнены для прямолинейного турбулентного течения. Одномерная аналитическая модель, для докритических условий, так же предложена С. Р. Шайном [17].

Особенности конструкции турбин ТНА ЖРД и объект исследования. При проектировании диаметр турбины ТНА ЖРД выбирается с учетом компоновки и обеспечения минимальных габаритов и лимитируется прочностью ротора турбины. Из анализа адиабатной работы известно, что при выбранном рабочем теле наибольшая величина адиабатной работы достигается при высоких температурах и больших отношениях давлений.

Применение высоких температур ограничивается работоспособностью конструкции. В ЖРД применяются неохлаждаемые турбины. Из за конструктивных особенностей и применяемых материалов температура рабочего тела перед неохлаждаемой турбиной ограничивается, как правило, для восстановительного газа 1000–1200 0С, для окислительного газа 700-900 0С. Чем большую температуру перед турбиной можно допустить, тем меньше должно быть давление перед турбиной. Из за особенностей конструкции турбины ЖРД выполняют одноступенчатыми и реже двухступенчатыми.

Высокие температуры рабочего тела приводят к температурным деформациям, в том числе и дисков турбин [18]. При проектировании проточных частей узлов и агрегатов ТНА ЖРД необходимо учитывать изменение температуры потока рабочего тела по длине рабочего канала, так как параметр вязкости является функцией температуры и определяет режим течения и как следствие потери, в частности дисковое трение и гидродинамические потери в проточной части.

Оптимальный уровень стабильности энергетических параметров турбонасосных агрегатов (ТНА) обеспечивается в процессе опытно-конструкторских работ путем корректировки геометрических размеров деталей и сборочных единиц газодинамического тракта, выбора технологических схем размерной обработки, сборки и испытаний турбин с привлечением значительного объема статического материала. В связи с этим моделирование энергетических параметров ТНА ЖРД, представляет актуальную научно-техническую задачу. Вопросы оптимизации параметров рабочего процесса и математическая модель ДУ рассмотрены в работе В. А. Григорьева [19], где проведен анализ моделей и раскрыты приемущества и недостатки для различных этапов проектирования.

При проектировании требования к ТНА формируются исходя из задач, выполняемых двигательной установкой (ДУ), в которую ТНА входит составной частью и с которой компонуется как единый блок. Требования к ДУ в полной мере относится и к ТНА: обеспечивать на всех режимах работы двигателя подачу компонентов топлива с требуемым расходом и давлением при высокой степени надежности и КПД; обеспечивать минимальные размеры и массу; простота конструкции и минимальной стоимости.

Основным объектом исследования, где реализуется потенциальное и вихревое вращательное течение, являются конструктивные элементы проточных частей газовых турбин ЖРД: подводящее и отводящее устройство, полости между статором и рабочим колесом [20].

Постановка задачи исследования. При обобщенной постановке задачи о течении жидкости при теплообмене с поверхностью агрегатов, таких как компрессоры, детандеры, насосы криогенных компонентов и т.п., необходимо учитывать изменение температуры потока по длине рабочего канала, поскольку вязкость, как функция температуры, в основном определяет режим течения и, как следствие, гидравлические потери [21].

Для случая течения несжимаемой жидкости необходимо и достаточно совместного решения уравнений движения и энергии в граничных условиях пространственного пограничного слоя [22], для сжимаемой жидкости необходимо дополнение системы уравнением состояния.

Процессы теплоотдачи в энергетических установках во многом схожи, но при анализе а выводе уравнений теплообмена для граничных условий ЖРД существуют определенные отличия. Основные отличия заключаются в следующем: экстремально высокие значения тепловых потоков, температур и давлений, наличие высоких скоростей потоков, начальное турбулентное состояние потоков в активной зоне, рабочие тела могут находиться в газообразном и жидком состоянии, эффекты кривизны поверхности, наличие градиентов плотности и сжимаемости, нестационарность тепловых потоков и наличие неустойчивости потоков в активной зоне теплообмена [23].

Закон теплообмена турбулентного течения температурного пространственного пограничного слоя. Интегральное соотношение уравнения энергии.

При числах Прандтля, меньших единицы (Pr<1 характерно для газообразных рабочих тел, в том числе и продуктов сгорания), толщина динамического пограничного слоя находится ниже толщины температурного пограничного слоя, т. е. δ<δ t (рис. 1). При очень низких числах Прандтля (жидкие металлы) молекулярная теплопроводность является основным механизмом переноса тепла и ею нельзя пренебречь даже в турбулентном ядре потока. При низких числах Прандтля термическое сопротивление распределено по всему сечению потока [24].

Примем, что в границе динамического пограничного слоя изменение температуры происходит за счет переноса скорости, а за его границей – только за счет молекулярной теплопроводности. Данное предположение хорошо согласуется с выводами Кейса, так как при очень низких числах Прандтля толщина динамического пограничного слоя в значительной степени меньше толщины температурного пограничного слоя. Соответственно, термическое сопротивление присутствует по всей толщине температурного пограничного слоя. В границах динамического пограничного слоя термическое сопротивление обусловлено турбулентным переносом тепла, а вне границ динамического пограничного слоя термическое сопротивление – молекулярной теплопроводностью.

Рассмотрим выражение толщины потери энергии температурного пограничного слоя [25]:

⁵ t

8 *' = f ^ 1 - LT dy .                        (1)

1ф о U V T5 To 7

Границы интегрирования толщины потери энергии (1) необходимо разбить на два характерных участка. Первый участок интегрирования лежит в границе толщины динамического пограничного слоя δ, второй участок интегрирования – в границе окончания толщины динамического пограничного слоя δ до окончания температурного пограничного слоя δ t .

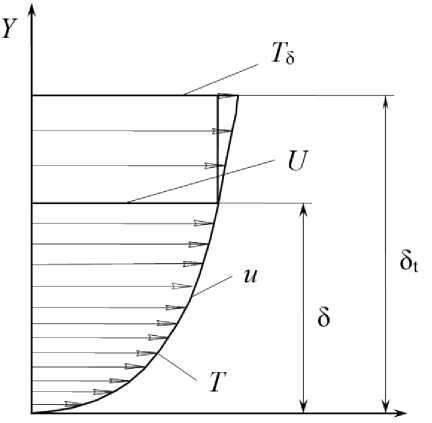
Рис. 1. Модель распределения температурного и динамического пограничных слоев при Pr < 1

Fig. 1. Temperature distribution model and dynamic boundary layers at Pr <1

Запишем выражение толщины потери энергии (1) для рассматриваемой модели распределения температурного и динамического пограничных слоев, с принятой моделью разбиения на два характерных участка интегрирования:

—

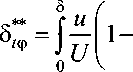
T - T o A

T ° - T o J

dy .

С применением уравнения (2) становится возможным определить вид закона теплообмена для случая Pr < 1. Для дальнейшего использования уравнение (2) необходимо проинтегрировать с учетом принятых законов распределения профиля скорости в пограничном слое. Далее последовательно рассмотрим сначала степенной профиль, потом градиентный.

Распределение динамического пограничного слоя аппроксимируем степенной функцией вида

U _| y A m

U .

Распределение температурного пограничного слоя аппроксимируем функцией вида

T - T o   ( У A m

—         .

T ° - T o   (° 1 J

Учитывая принятую модель распределения динамического и температурного пограничных слоев и функции распределения параметров динамического и температурного слоев, запишем выражение для толщины потери энергии:

°.r

** fl У I m

° t ф^— J lgl

0 ^{(U J}

1 -

f

(° t J

1A

m

° l y A m

-

У

1 a A m

(

J

(° t J

(         J

dy .

Учтем, что в первом члене уравнения (3) профили распределения динамического и температурного пограничных слоев совпадают. Тогда в границах интегрирования первого члена уравнения (3) совпадают и толщины температурного и динамического пограничных слоев, т. е. δ t = δ. Рассматривая второй член уравнения (3) отметим, что изменения динамического пограничного слоя вдоль оси Y в границах интегрирования не происходит и скорость потока равна скорости потока в ядре течения. Тогда распределение динамического пограничного слоя во втором члене уравнения (3) запишется в виде

U l У A m 1 —        — 1 .

U (°J

Так же во втором члене уравнения (3.3) изменение эпюры температурного пограничного слоя происходит только за счет молекулярной теплопроводности. Необходимо учесть, что для данного участка эпюра профиля выглядит следующим образом:

T - T ^—X y .

T ° , - T °     °,

Учитывая условие сопряжения температурного и динамического профилей для физической модели теплопроводности при Pr < 1 (рис. 2) с конвективной составляющей, запишем:

T ° - T o

T - T o

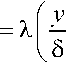
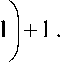
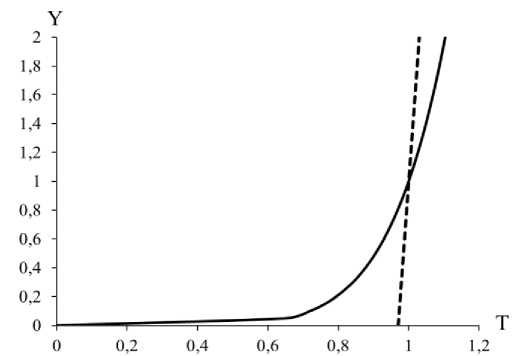
Рис. 2. Сопряжение температурного и динамического профилей для физической модели при Pr < 1

(       – динамический пограничный слой со степенным распределением скорости;       – температурный пограничный слой)

Fig. 2. The pairing of temperature and dynamic profiles for the physical model at Pr <1

(        – dynamic boundary layer with a power-law velocity distribution;

– temperature boundary layer)

Перепишем выражение для толщины потери энергии с учетом принятой двухслойной модели распределения температурного пограничного слоя с наличием теплоотдачи при условии Pr < 1:

5.Г,

**      I y I m

⁵ 1 » = J (sJ

y I m

5 J

AI

1 — I y I m

I y I ^m

1 —

V 5 J

5 t(

5 V

5 t(

Проведем замену переменных в уравнении толщины потери энергии температурного пограничного слоя (4):

5. A1

1 —I y I • V s J

dy,

A 1 = I y I m i VsJ

5 1(

Рассмотрим первый член уравнения:

5/     I

A1 = f l y I m 0 ^v5j

a I 1-I y I m w

dy =

m 5

( m +1 ) ( m + 2 )

Определим второй член уравнения для определения толщины потери энергии температурного пограничного слоя:

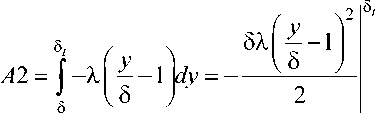
X ( 5-5 1 ) ²

Тогда выражение для толщины потери энергии (4) с учетом (5) и (6) запишется как

**         m 5        Х ( 5- 5 t )

' t ^ф = ( m +1 )( m + 2 )       25

Приняв во внимание, что

— = x 5 1

после преобразований получим или

**

⁵ t ф

**

⁵ t ф =

m 5

( m +1 )( m + 2 )

m 5       5X ( x -1 ) ²

( m +1 )( m + 2 )      2 x ²

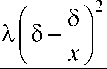
m

( m + 1 )( m + 2 )

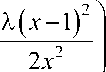
Для закона теплообмена в виде критерия Стантона, необходимо определить производную температурного пограничного слоя на стенке поверхности теплообмена. Так как производная не существует формально при m<1, определяем ее из принятой двухслойной модели турбулентности с ламинарным подслоем. Учитывая, что в ламинарном подслое профили динамического и температурного ППС совпадают, исходя из принятой модели

_df T - T

I T T- T O J y = 0

выразим толщину динамического пограничного слоя из (9):

**

_____________51 ф_____________ m        X( x -1)2

( m +1 )( m + 2 )      2 x '²

Тогда толщина температурного пограничного слоя определится как

5 1 =

**

51 ф xm       X( x -1)

( m +1 )( m + 2 ) -   2 x

Используя выражение для толщины потери энергии (12) и проведя преобразования для производной на стенке поверхности теплообмена профиля распределения температурного пограничного слоя (10), а также учитывая закон теплообмена, получим или

St =

X p C p U

U аЛv

U xm

^a Л ^v

**

⁵ 1 ф

_V ( m +1 )( m + 2 )

—

xm

m + 1

—

m + 1

² x   )

St      X p CpUm+1

•

V

(m +1)( m + 2)     2 x m-1

a m ^{- 1} v

•

( s * ; ) m

.

Учитывая степень турбулизации профилей пограничных слоев при m = 7 , запишем

распределения теплового и динамического

St =

X

•

p C p U ^a/v^0,75 (5 ** )^0,25

•

x

2  0,25

—

2 x

.

Для практической реализации закона теплообмена необходимо определить значение а_л. Оно находится из условия смыкания ламинарного подслоя с турбулентным профилем [25] при у = 5_Л и степени профиля 7:

^а л   1,5

xm

( m +1 )( m + 2 )

xm

—

m + 1

xm

( m +1 )( m + 2 )      2 x

( m + 3 )

—

( m +1 )( m + 2 )      2 x

( m + 3 )

m + 1

0,01256

.

Теперь окончательно получим выражение для определения коэффициента ламинарного подслоя турбулентного профиля распределения температурного пограничного слоя для принятой модели:

а _л = 12,5496 Pr ¹⁸ .

Запишем интегральное соотношение уравнения энергии ППС с учетом закона теплообмена (14):

•

dHф e** , дф  tФ

1 д / 5?** \      1 д / _x** \       1

нф •аф' 1 ф)+нф •фф' ’У нфнф xm

—

m + 1

+

1 н ф н ф

•

дHФ ,  = X дф tф      — p CpUm+1

(m +1)( m + 2)     2 x m-1

a m ^{- 1}v ~

X

^X ~

( 6 * • ) " + ‘

^т О ^г )

Р C p ( T₆-T o ) .

Принимая относительную характерную толщину ** 1. ° 1 у

J              , г  6tф

запишем

1 д / q**\ J д / c ** \      1

H y 'дф⁽ t ^{ф) +} H ^ ^V t ^{ф) +} h ^ h ;

•

dHу <** , д 61 ф + дф

xm

2 m + 1

—

+

J

•

ф у

дH, ..      X ду t ф      —

Р C_pU^{m + 1}

(m +1)( m + 2 )     2 x m-1

a m ^{- 1} v

X

к

;

^X ~

( 6* • ) - + 1

Р C p ( T > - T o ) .

Рассмотрим прямолинейное равномерное течение при следующих граничных усдовиях:

8              д H,   д H

— — 0, H у — H ф — 1,     —— о [26].

ду                дф   ду

Тогда интегральное соотношение уравнения энергии для прямолинейного равномерного течения (18) преобразуется к виду xm

—

2 A

2 m + 1

д **       X дф tф      — р CpUm+1

(m +1)( m + 2)     2 x m-1

a m ^{- 1} v

—

^т Ф 0 ( ' ^{+ Е} 2 )

( 6~ ) m + 1    ^{Р C}P ⁽ T  T ⁰ )

Для вращательного течения, реализующегося в полостях энергетических и энергосиловых агрегатов, линия тока представляет собой кольцевую линию. Выполним запись интегрального соотношения уравнения энергии (18) в цилиндрических координатах, учитывая, что для осесимметричного течения при е= const выполняются соотношения ф — а, у = R, Hф — R,

д H _ф ду

^R — 1, H — 1, ^Hv — 0, — — 0 [27; 28]: дR     у     дф     дф xm

—

2 A

2 m + 1

^д   **    J г **

J г---6,т +--6, — дR t ф   R  t ф

X р CpUm+1

(m +1)( m + 2)     2 x m-1

a m ^{- 1} v

—

^Т Ф 0 ( ' ^{+ 6} 2 )

( § ** ) m + 1    ^{Р C}P ^{( Т}   T ⁰ )

Интегральное соотношение уравнения энергии (20) необходимо для записи и определения толщины потери энергии температурного пространственного пограничного слоя, входящей в выражение для определения локального коэффициента теплоотдачи в виде критерия Стантона.

Локальная теплоотдача при различных законах течения внешнего потока.

Для прямолинейного равномерного течения пренебрегаем диссипативным членом и получим интегральное соотношение уравнения энергии (19) в следующем виде:

m + 1

xm

—

d „**       x аФ5 t■          -2- pCpUm+1

(m +1)( m + 2)     2 x m-1

a m ^{- 1} v ~

•

( 5 ** ) m + 1

.

Разделим переменные и проинтегрируем от нуля до текущего значения переменных:

**

⁵ 1 ф =

**

⁵ t ф          2

⁵ * ф ) ^{m + 1} d ⁵ * ф =

x p CpUm+1

xm       X ( x - 1 )

(m +1)( m + 2)     2x m-1

^{a m} - 1 H ²

2 m + 2

m + 1

ф

J d Ф, (22)

m + 1

3 + m

xm

—

( m + 1 )( m + 3 )

Хф

_VP C p U m + 1 _V

(m +1)( m + 2)     2 x m-1

a m ^{- 1} v

m + 1 3 + m A 3 + m m +1 J

С учетом выражения закона потери энергии (23), запишем:

теплоотдачи (14) и полученного выражения для толщины

xm

m + 1

—

St =

X p CpUm+1

(m +1)( m + 2)     2 x m-1

a m ^{- 1}v~

. (24)

2 m + 2

m + 1

3 + m

xm

( m + 1 )( m + 3 )

m + 1

—

Хф

2 _vp C p U m + 1 _?

V

(m +1)( m + 2)     2 x m -1

a m ^{- 1} v

J

m + 1 3 + m A 3 + m m +1 J

Проведя преобразования и учитывая выражения для критериев Прандтля

Рейнольдса

( Re = £ U ₽ A

V       н J

Pr =

^C p A

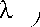
и

получим выражение для определения локального коэффициента

теплоотдачи в виде критерия Стантона прямолинейного равномерного течения при степенном профиле распределения эпюры скорости и температуры при Pr<1:

St =   '

m + 1

Pr m + 3

xm      X ( x -

( m +1 )( m + 2 )      2 x

m + 3

( m +1)

a m 1 ( m + 3)Re₍₇

.

Рассмотрим вращательное течение. Пренебрегая диссипативным членом в интегральном соотношении уравнения энергии (20), получим

8   *«\ J s „**        X

JS (RR (§ t J+ R 5 t ф        _J_ pCpUm+1

xm

m + 1

—

X

(m +1)( m + 2)     2 x m-1

a m ^{- 1} v ~

•

—V=⁰. ( s * ф ) m + ¹

(U

Учтем, что реализуется вращательное течение по закону твердого тела I — = to = const I, k R            J

тогда уравнение (26) преобразуется к виду

xm

m + 1

**

8 e.**   S t ф X dR tф  R         2

J spC_p to ^{m + 1}

( m +1 )( m + 2 )

m - 1

a m ^{- 1} v

Введем промежуточные обозначения:

**

^s t ф = y ,

xm

—

2 x

—

•

= 0.   (27)

B =

X

J sp C p to ^{m + 1}

(m +1)( m + 2)     2 x m-1

a m ^{- 1} v ~

Тогда

dy  y dR R

—

B -r=o.

R m + 1 y m + 1

Данное уравнение решается методом подстановки y = и 3 :

B

2      2      2, um+13 m+1 Rm+1

B

2      2      2 .

U m + 1 3 m + 1 R m + 1

du „ d 3	3
— 3 + —	и + и— =•
dR   dR	R
f d 3  34	du
u — + —	+ 3— =
k dR R j	1     dR

.

R^{m + 1} ( s ** ) ^{m + 1}

m + 1

.

О                  „              d »  » А       П 1

Функция У должна удовлетворять условию--1— = 0, тогда У = — , откуда находим dR R           R m'! BR2 (m + 3)

U = m +1 ---

**

t ф

1 m + 3 BR ² ( m + 3 )

= — m + 1 ----^-----^

R

= m + 1

,

xm

m + 1

—

**

^ t ф =

m + 3 m + 1

X

J £р C_p to ^{m + 1}

(m +1) (m + 2)     2 x m-1

a m ^{- 1} v ~

• ( m + 3 )

m - 1

• R m + 1 .

С учетом выражения для закона теплообмена (14) и полученного выражения толщины потери энергии (28) определим критерий Стантона для вращательного течения по закону твердого тела степенного профиля распределения температурного пограничного слоя и Pr<1:

xm

m + 1

—

St =

m + 3 m + 1

X

J £p C_pU^{m + 1}

(m +1)( m + 2)     2 x m-1

a m ^{- 1}v~

xm

m + 1

.

m + 1    (29)

—

X

J £p C p to m + 1

(m +1) (m + 2)     2 x m-1

a m ^{- 1} v

•

( m + 3 ) m - 1

A______ ' R m + 1

Проведя преобразования и учитывая критерии Прандтля

I        ^Cp I

Pr = ^-- p v       ^X J

и Рейнольдса

Re = U

, определим локальный коэффициент теплоотдачи в виде критерия Стантона

для вращательного течения по закону твердого тела для случая Pr<1:

2(m + 3) - 4

^St       m + 1

Pr m + 3 ^v

2 J £

( m +1) ^{m + 3}

a m ^{- 1} Re ( m + 3)

xm

X ( x -1 ) 2 |^{( m + 1 )( m + 3 )}

( m +1 )( m + 2 )      2 x

.

Рассмотрим вращательное течение, которое осуществляется по закону свободного вихря (UR = C = const), тогда интегральное соотношение уравнения энергии (26) примет вид xm

m + 1

** d 5 t ф dR

**

₊ ⁵ 1 ф

R

—

X

J Sp C/'m ' ¹

(m +1)( m + 2)     2 x m—1

a m ^— 1 v ~

—

♦

R m + 1

~ = °"

( 5 ** ) m + 1

Проведя замену:

**

⁵ 1 ф = y ,

xm

m + 1

—

решение уравнения

D —4

J sp C p C^{m + 1}

(m +1)( m + 2)     2 x m—1

a m ^— 1 v

,

к

(31) ведем аналогично случаю вращательного течения по

закону

твердого тела для Pr<1 подстановкой y = u3, причем m+1

1       D m + 3 R R

3 = — , u =----—

R          m + 1

2 m + 3

Тогда толщина потери энергии определится в виде m + 1

„ **    f D ) m + 3 „

⁵ 1 ф=Нг] ^R ,

.

или, после подстановки:

**

⁵ 1 ф =

X

J sp C_pC m + 1

xm

—

2 m + 1

m + 1 m + 3

(m +1)( m + 2)     2 x m—1

a m ^— 1 v ~

/2

• R .

Подставив полученное выражение для определения толщины потери энергии (34) в

выражение закона теплообмена (14), получим

xm

m + 1

—

St = -

X p CpUmx

(m +1)( m + 2)     2 x m—1

a m ^— 1 v ²

V

m + 1 m + 3

1 m + i

X

J £ C p C m ^

m + 1

/ 2 m + 3

V                                                              7

Проведя преобразования и учитывая критерии Прандтля

f      ^c_p 1

Pr = ^ p

V        ^X 7

и Рейнольдса

f Re = U 1

V      Ц 7

определим локальный коэффициент теплоотдачи в виде критерия Стантона

для вращательного течения по закону свободного вихря для случая Pr<1:

St = -^j- m +i

Pr m + 3 V

2 J £

a ^{m —1 a} л

xm

Re ^ ( m +1 )( m + 2 )      2 x

,² 11 m + 3

Таким образом, определены выражения для локального коэффициента теплоотдачи в виде критерия Стантона при различных законах течения внешнего потока для степенного профиля распределения скорости в пограничном слое для случая Pr<1.

На рис. 3 показано влияние критерия Прандтля на трение и теплообмен по данным различных исследований [29]. В области значений чисел Прандтля Pr>1 полученные теоретические зависимости для безразмерных коэффициентов теплоотдачи в виде критериев Стантона, с учетом интегрального соотношения уравнения энергии, хорошо совпадают с зависимостями других авторов. C f представляет коэффициент трения.

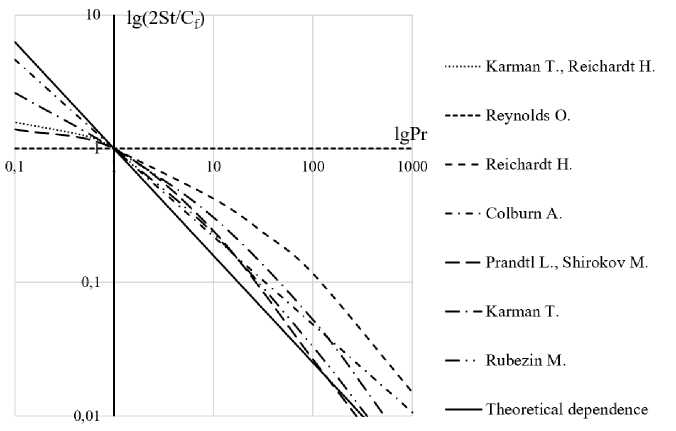
Рис. 3. Сравнение различных теорий аналогии между трением и теплообменом в турбулентных потоках при Re=107

Fig. 3. Comparison of various theories of the analogy between friction and heat transfer in turbulent flows at Re=107

Коэффициент теплоотдачи в виде критерия Нуссельта, представляет произведение критериев Стантона, Рейнольдса и Прандтля Nu = St RePr.

На рис. 4 представлен график распределения безразмерного коэффициента теплоотдачи в виде критерия Нуссельта для турбулентного вращательного течения по закону «твердого тела» при критерии Прандтля Pr = 0,7 . Теоретическая зависимость определенная по модели с конвективной составляющей дает наилучшее совпадение с результатами экспериментальных исследований и не превышает 3,5 %. Так же наилучшее схождение результатов определяемых по модели с конвективной составляющей дают теоретическая зависимость полученная по аффинноподобной модели и теоретическая зависимость полученная J. M. Owen [30] и не превышают 1,5 и 2,66 % соответственно.

Расхождение теоретических данных полученных по теоретической зависимости с использованием модели с конвективной составляющей с зависимостью полученной И.В. Шевчуком [31] составили 9,5 %. С зависимостью полученной L.A. Dorfman [32] 16,7 %.

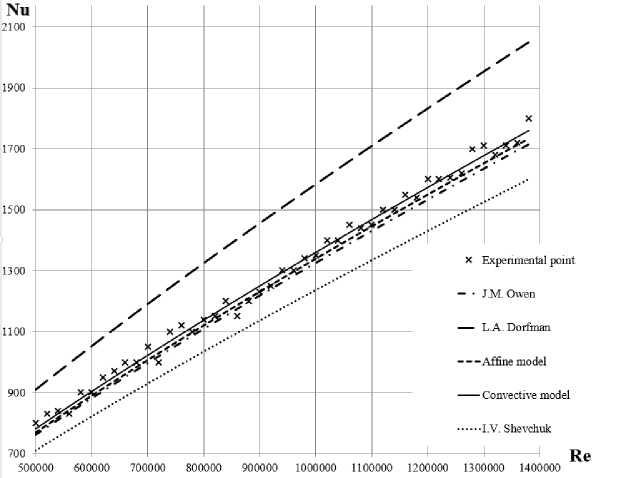
Рис. 4. Зависимость безразмерного коэффициента теплоотдачи турбулентного вращательного течения по закону твердого тела при Pr=0,7

• 4. The dependence of the dimensionless heat transfer coefficient of turbulent rotational flow according to the law of a solid body at Pr=0.7

На рис. 5 представлен график распределения безразмерного коэффициента теплоотдачи в виде критерия Нуссельта для турбулентного потенциального вращательного течения по закону «свободного вихря» при критерии Прандтля Pr = 0,7 . Теоретическая зависимость определенная по модели с конвективной составляющей дает хорошее совпадение с результатами экспериментальных исследований и не превышает 5 %.

Расхождение теоретических данных полученных по теоретической зависимости с использованием модели с конвективной составляющей и по модели с аффиноподобными профилями не превышает 3,5 %. Теоретические зависимости полученные по моделям распределения температурного и динамического пограничных слоев с конвективной составляющей и с аффинноподобными профилями при Pr = 0,7 дают достаточно близкие результаты, в связи с близким подобием распределения температурного и динамического слоев и близки к случаю Pr = 1.

Из графика рис. 5 видно, что полученные теоретические зависимости находятся в области определяемой другими авторами, но сравнение результатов не корректно, так как теоретические зависимости получены для других граничных условий потенциального вращательного течения по закону «свободного вихря».

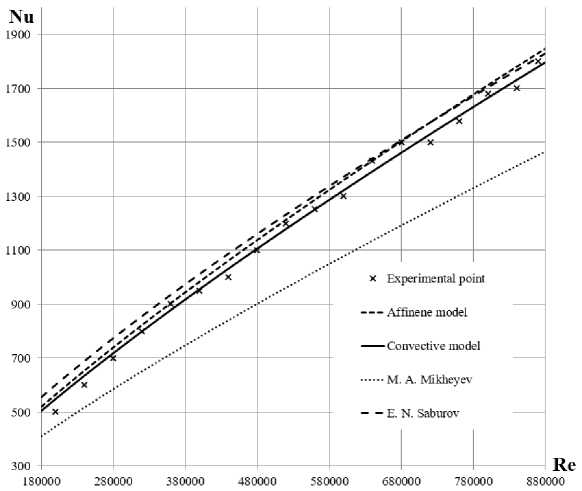
Рис. 5. Зависимость безразмерного коэффициента теплоотдачи турбулентного вращательного течения по закону свободного вихря при Pr=0,7

Fig. 5. The dependence of the dimensionless heat transfer coefficient of a turbulent rotational flow according to the free vortex law at Pr=0.7

Полученные теоретические зависимости и зависимости других авторов находятся в едином диапазоне и пригодны для инженерных расчетов и анализа данных. Необходимо отметить, что на безразмерный коэффициент теплоотдачи в виде критерия Нуссельта существенно влияют граничные условия течения и теплообмена, такие как скорость, вязкость, плотность и градиент температур рабочего тела и поверхности теплообмена.

Заключение . Получено интегральное соотношение уравнения энергии температурного пространственного пограничного слоя, позволяющего вести интегрирование по поверхности любой формы, необходимое для определения толщины потери энергии. Выражения для определения толщин потери энергии температурного пространственного пограничного слоя необходимы для определения локальных коэффициентов теплоотдачи для характерных случаев течения с учетом теплообмена.

Аналитическим путем получены выражения для определения локального коэффициента теплоотдачи в виде критерия Стантона для прямолинейного равномерного течения потока, вращательного течения по закону твердого тела и вращательного течения свободного вихря степенного профиля распределения параметров динамического и температурного пограничного слоя для случая Pr<1.

Аналитические выражения для коэффициентов теплоотдачи хорошо согласуются с экспериментальными данными и зависимостями других авторов.