Теплоперенос в щелевых каналах

Введение. С целью создания дополнительной защиты боевой одежды пожарных от перегрева была разработана конструкция специального вкладыша, содержащего элементы из материала с памятью формы [1]. Устройство образует щелевое пространство, заполняемое азотом, поступающим из специального баллончика. Для вкладыша необходимо знать теплотехнические характеристики, в частности, коэффициенты теплоотдачи для вычисления тепловых потоков. Постановка задачи, тщательная и корректная, приведена в [2], а аналитическое решение представлено в данной статье.

Цель и задачи исследований : проведение анализа системы дифференциальных уравнений применительно к данному конкретному случаю теплопереноса; получение расчетных формул для местного (локального) и среднего коэффициентов теплоотдачи α; расчет тепловых потоков Q для двух инертных газов – азота и гелия.

Условия и методы исследований . Между стенками вкладыша возможно как независимое развитие пограничных слоев, когда восходящий и нисходящий пограничные слои не взаимодействуют друг с другом, так и наложение слоев с образованием сложных циркуляционных контуров. В данной работе исследуется перенос теплоты для случая независимого формирования пограничных слоев.

В работе [2] представлены уравнения теплоотдачи, энергии, движения и сплошности (уравнение сохранения массы). К ним введены методические дополнения: 1) при выводе уравнения энергии поясняется формула конвективной составляющей теплового потока в выражении первого закона термодинамики для потока жидкости или газа (известные литературные источники не содержат таких сведений, что затрудняет понимание сути уравнения энергии); 2) предлагается простой вывод уравнения сплошности.

Система уравнений:

– теплоотдачи α =- ^λ ; ⁽an⁾_c ;

Dt и 2 .

– энергии          dr =  ∇ t ;

D ω x      ¹⁵P । ~ _л

– одномерного движения ρ = -    +gxρ- aτρox л л . .    ^2 ωX

ρ g X β Δt + ^ω ;

a ( ρω _x )     a ( ρω у )     a ( ρω )

– сплошности      + (ρω ) + (ρω) =0, ox ay az где λ – коэффициент теплопроводности, Вт/(м·К); ρ – плотность, кг/м3, β – коэффициент объемного расширения, 1/К; μ – коэффициент динамической вязкости, Па·с; ω – скорость потока, м2/с.

Для решения системы уравнений с целью получения формулы для коэффициента теплоотдачи необходимо знать условия однозначности, включающие в себя физические свойства потока жидкости или газа, геометрические характеристики теплоотдающей поверхности, начальные распределения температуры для нестационарных задач, а также граничные условия, определяющие теплообмен на границе стенка - поток.

В данном исследовании изучается теплоперенос в условиях стационарного режима между поверхностью нагретой вертикальной пластины и потоком газа, находящегося в движении за счет свободной конвекции.

Начало координат расположено у нижней кромки пластины. Ось x направлена вертикально, ось y – по нормали к поверхности. Вблизи стенки образуется пограничный слой, толщина которого возрастает по мере перемещения потока (рис. 1).

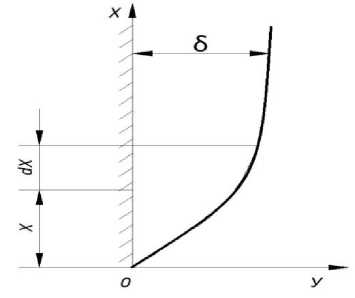
Рис. 1. Формирование пограничного слоя (δ – текущая толщина пограничного слоя)

Вначале система уравнений подвергается анализу с учетом следующих упрощений [3]:

– физические свойства, кроме плотности, постоянны и не зависят от температуры (в том числе и коэффициент объемного расширения);

__ rx U ω X

– при стационарном режиме = 0 и     = 0 ;

– перенос теплоты происходит в направлении оси y;

– движение одномерное, направлено по оси х, скорость потока ω х ;

– сила давления незначительна, и ею можно пренебречь, тогда градиент давления равен нулю:    =0 ;

– сила тяжести минимальна, поэтому ею можно пренебречь;

– температура нагретой поверхности практически одинакова и постоянна, поэтому принимается условие: t = const ;

– температура в сечении изменяется только в направлении y.

В данной статье рассматривается теплоотдача только с нагретой стороны вкладыша, имеющей температуру t .

Для упрощения вида формул в процессе решения используется избыточная температура ϑ=t - t , где – текущая температура пограничного слоя, t – температура стенки. На стенке _с = t -t ж , где t ж – температура газа вдали от стенки. Уравнение теплоотдачи получит следующий вид:

=

λ

$c ydy)y=0

.

На основании многочисленных исследований теплоотдачи вертикальной пластины при свободном движении потока можно принять, что температура в пограничном слое изменяется по параболическому закону:

= с (1- ) .              (2)

Плотность газа при малой разности температур представляется в виде слабой линейной зависимости от температуры:

ρ = ρж (1-β ), где ρж – плотность вдали от стенки при температуре потока tж.

Тогда для подъемной силы можно написать

–ρ g β = - ρ ж g β + ρ ж g х ² β^{2 2}.

Здесь о gх2 β2 2 →0, так как β ≪1 [4].

Тогда можно записать

= жg β .(6)

Граничные условия:

– при  =0

– при  =

В (6) подставляется из (2):

сс

= ^-pс^{9 р}с( ^(1-F = “^(1-F ■ (7)

Обозначая ^-^ = a , уравнение (7) можно записать так:

Уравнение (2) имеет граничные условия:

– на стенке при y = 0    = _с ;

– на внешней границе слоя при =   =0.

Формула (2) дифференцируется:

d2cox dy2

^-a ( ^1-2 ^⁺S) ■

откуда

d-d dy

2tic , 2VC

-  +    =

-

(1- ),

( )

и уравнение теплоотдачи (1) получит следующий вид:

λ

.

Таким образом, для определения коэффициента теплоотдачи требуется найти толщину пограничного слоя δ. С этой целью используется уравнение движения, в котором с учетом принятых условий присутствуют только подъемная сила и сила трения:

0 =- ρ g β + ^ω ,           (5)

где – коэффициент динамической вязкости, Па с.

Это уравнение дважды интегрируется:

da)_x                у² ,   1

=- ( -  +     ) + С ;

dy        V <5 Зб²⁷ J ¹

(7а)

=- (  -   +     )+ С + С .

*       \2    38⁷   128^{2 7} J            ²

С учетом граничных условий определяются постоянные интегрирования:

Ci = a -; С2 = 0, и уравнение (7а) получит вид

=  (   -     +      -       ) .      (8)

* M7 2 7     3(57     12S2 7 J        ' '

Формулу (8) можно исследовать на максимум, для чего достаточно использовать выражение, стоящее в скобках. Максимальное значение скорости в пограничном слое имеет место при значении ~ 0,375 .

Распределение скорости по толщине пограничного слоя приведено на рисунке 2.

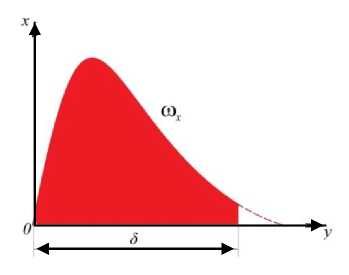
Рис. 2. Распределение скорости согласно уравнению (8)

В итоге получены формулы среднеинтегральных значений температуры и скорости в пограничном слое:

– температуры (с использованием (2))

« = ∫ ^dx = ∫ >c (1--_s ^{) 2}dy =   ;    (9)

– скорости

_  1 r8     —Ров^с^²

^x = ∫) M_xdy =          .         (10)

Для элементарного участка поверхности dF пластины высотой dx и протяженностью z можно сформировать условие теплового баланса: тепловой поток Qk , передаваемый от поверхности к среде за счет конвективной теплоотдачи, равен тепловому потоку Q_P , воспринимаемому средой в изобарном процессе, т. е.

Qk = или dQk =     .(11)

Согласно закону Ньютона – Рихмана, dQk =       =.

С учетом (4)

dQk =λ dedx z .(12)

В свою очередь, dQp , согласно первому закону термодинамики равно произведению изобарной теплоемкости на массовый расход потока и на изменение температуры потока, т. е.

тогда

dQp =                 .(14)

Выражение (12) и (14) подставляют в (11):

^3p°^e^^c6³d6 = ^λ dx.

40M

После интегрирования

3p2°3^c84d8 = λx + С.(15)

Постоянную С определяют из условия на нижней кромке пластины: при x =0 8 =0, откуда следует что

С = 0.

Уравнение (15) дает возможность определить толщину пограничного слоя:

⁵ =4,23 √ ^pFf ^λ l#cg .           (16)

Подставив (16) в (4), получим выражение для местных коэффициентов теплоотдачи:

=

2 λ

<5

0,473

⁴^ CpPPoBc λ ³g

.

Для приведения уравнения (17) к безразмерному виду обе части умножаются на , а подкоренное выражение на

:

dQp = с_pdm d .             (13)

Массовый расход dm =( Po^x^f ) , где d ( 8f ) – элементарная площадь сечения потока.

С учетом (10)

СрРоЭрдс λ ³ X⁴ Ц ЦХ λ⁴ F , ax = 0,473 √ gjyyx^ gcp

ax 4

_λ =0,473 √

dm =( Po P°aL, f)=3p°aps2 fd8, \T 40g                       , dm =( Po ^1X7 f)=зр20д^с ^2^ , \       40g                               ,

где -  =    – критерий Нуссельта; 9P. < =         = Gr – критерий Грасгофа; λ = Pr – критерий Прандтля.

Тогда критериальное уравнение для расчета местных коэффициентов теплоотдачи на вертикальной пластине при свободном движении потока получит вид

= 0,473(      ) ^,   .             (18)

Средний по высоте пластины коэффициент теплоотдачи определяется по формуле

=          =          ^,      =      ^,   =        ,

, и расчётное уравнение получит вид

Nu = 0,67( ) ^, . (19)

Для заполнения щелевого пространства защитного вкладыша от перегрева следовало выбрать доступный и дешевый инертный газ [1], физические свойства которого обеспечивали бы наименьшие значения тепловых потоков Q. Были рассмотрены два газа – азот и гелий. Расчеты средних по высоте стенки коэффициентов теплоотдачи по уравнению (19) и тепловых потоков для этих газов с использованием [5] приведены в таблицах 1 и 2.

Таблица 1

VC	чс	Рг	Gr 10 ’ 5	( G г Р г)10 - 5	Nu	a, Вт/( м 2 K)	Q, Вт
70	60	0,696	4,19	2,916	82,32	5,91	9,46
60	50	0.698	4,68	3,36	84,69	6,03	9,65
50	40	0.699	5,24	3,3619	87,15	6,1	9,76

Таблица 2

VC	VC	Pr	Gr 10-5	( Gr Pr10-~ 5	Nu	a, Вт/( м 2 K)	Q, Вт
70	60	0,675	9,04839	6,1077	17,61	7,086	11,33
60	50	0.675	8,5249	5,7543	17,35	7,114	11,3
50	40	0.675	7,933	5,355	17,4	7,162	811,4

Расчет среднего коэффициента теплоотдачи для азота

Расчет среднего коэффициента теплоотдачи для гелия

Анализ полученных данных позволил сделать вывод, что принятым требованиям удовлетворяет азот. Значения тепловых потоков Q не превышают 5 кВт/м2, что согласуется с требованиями к боевой одежде пожарных.

Таким образом, в статье приведено решение системы дифференциальных уравнений, получены уравнения для расчета местного (локального) и среднего по высоте потока коэффициентов теплоотдачи в условиях стационарного теплопереноса между поверхностью нагретой вертикальной пластины и потоком газа, находящегося в движении за счет свободной конвекции, а также выполнены расчеты тепловых потоков для инертных газов.

Выводы

• 1.    Сформулированы упрощения для решения системы дифференциальных уравнений конвективного теплообмена.

• 2.    Получены уравнения для вычисления местного (локального) коэффициента теплоотдачи и среднего по высоте плоской стенки коэффициента теплоотдачи для случая свободного движения потока газа в ограниченном пространстве.

• 3.    Результаты анализа системы дифференциальных уравнений позволяют рассчитать тепловые потоки для щелевых пространств в условиях переноса теплоты, что достаточно часто встречается в технических устройствах, в частности, для уменьшения тепловых потерь в окружа-

• ющую среду (создание тонких воздушных слоев в обмуровке паровых котлов и промышленных печей, тепловой изоляции трубопроводов отопления и горячего водоснабжения и т. д.).

• 4.    Выполнены расчеты тепловых потоков для инертных газов – азота и гелия, результаты которых позволили сделать вывод, что для заполнения пространства защитного вкладыша следует использовать азот.