Теплопроводность в однородной полосе с линейным изменением толщины при граничных условиях первого рода

Введение. Процессы в геометрических областях с изменяющимися во времени границами реализуются в различных приложениях. В ракетно-космической и авиационной технике – это управление фронтом горения в твердотопливных двигателях и повышение эффективности абляционной защиты обтекателей летательных аппаратов в плотных слоях атмосферы [1]. В [2] отмечается необходимость учета теплопереноса при росте кристаллов в формовке заготовок их жидкого металла. В химической и пищевой промышленности с помощью таких задач оценивается усушка материалов [3]. Современное применение подобных постановок отмечается в криомедицине [4]. Кроме того, учитывая математическую аналогию между законами Фурье и Фика, большой массив задач с подвижными границами встречается при переносе массы диффузией [5].

Систематизация и формализация математических задач с движущимися границами для различных типов уравнений математической физики были выполнены в [6], где одновременно были обозначены основные подходы к решению таких задач. В [7] были представлены оригинальные методы аналитического решения широкого класса параболических уравнений с различными начальными и граничными условиями с движущимися границами. Дальнейшее развитие такого подхода представлено в [8, 9] в контексте полуограниченных областей.

x                     В данной работе, используя идею перехода к новым координа там с Якобианом отличным от нуля, в которых исходная задача формулируется в области с фиксированными границами, рассмот-h0        рено решение нестационарного уравнения теплопроводности с граничными условиями первого рода на неподвижной и движу-0               щейся к ней по нормали границе бесконечной полосы.

Рис. 1. Расчетная схема

Постановка задачи. Рассматривается бесконечная горизонтальная полоса высотой h0 из однородного материала с изотропной температуропроводностью a. Начало координат расположено на нижней покоящейся границе (рис. 1), поддерживаемой при температуре t . В начальный момент времени (температура по высоте полосы постоянна и также равна t0 ) начинает двигаться верхняя граница, имеющая постоянную температуру t1 , по нормали в направлении неподвижной границы со скоростью и = const. В выбранной системе координат математическая формулировка задачи такова:

5 1 ( x, т )      5 2 t ( x, т ) „     = а      о    ; 5 т         5 x 2	(1)
1 ( x , 0 ) = 1 о ;	(2)
1 ( 0, т ) = 1 о ;	(3)
1 [ h ( т ) , т ] = 1 1 ;	(4)

(для определенности пусть 1 1 >  1 0 )

h ( т ) = A q - ит ,                                         (5)

где т - время; x - координата; 1 (x, т) - локальная температура в полосе. После введения безраз- мерных зависимых и независимых переменных

0 = та/hO , X = x/Aq , T(X,0) = [1(x,т)-tо]/(t1 -10), H(0) = h(т)/h0 = 1 -a0, A = uh0/a система (1)–(5) примет вид

5 T ( X , 0 )   5 ² T ( X , 0 )

—■—- = — 9—-;(6)

T(X,0) = 0 ;(7)

T (0,0 ) = о;(8)

T [ H (0) ,0] = 1;(9)

H (0) = 1 - A0.(10)

Решение. Сделан переход от системы координат ( X, 0 ) к новой автомодельной системе координат ( Уп ) по правилу

^ = 1 - А0, п = 0.(11)

Этот переход взаимооднозначен ввиду неравенства нулю Якобиана, причем зависимая искомая функция будет

^(£,7) = T[X(<п)0(£П)] ,(12)

относительно которой система (6)–(10) запишется следующим образом:

(1 - АП )2       ._ у - а, )д“1|П) +£211^ ;(13)

Н(^,о)=о;(14)

^(0,7 )=0;(15)

Q(1,n ) = 1.(16)

Представим функцию в виде произведения двух функций

n(^,n ) = q (^п ) W (^п ).(17)

После подстановки (17) в (13) имеем

(1 - Ап)2 awif,,) = 8^+M(Лп)^+N(,п) Wу. П), дп        ду2

где

M ( ^ , п ) = ^{— А} А ^{1 — А} п ) +   ,2 х^д q ⁽ ^ ! ^п ) ,

q ( 5 , п )    д ^

N ( ^п ) = q ( ^ , п )

— А ^ ( 1 — А п )⁸-^ + ^{д А}^ ^п

⁽       ) д ^        д ^ ²

—

( 1 — А , ) ^{2 Й}? ⁽5 , ^п

^V      ’ дп

.

Выберем q ( ^п ) так, чтобы M ( ^ , п ) = 0 • Этому условию удовлетворяет функция q ( ^ , п ) = С ( п ) exp ¹ А ^ ² ( 1 — А п ) ,

где С ( п ) - неизвестная функция, которая определена из (20) таким образом, чтобы N ( ^ , п ) = 0, тогда

С ( п ) = W1 — А п .

Таким образом, из (17) и (21), (22) следует

п(^п )=Wrs,r)

V1 — А п

exp ¹ А ^ ² ( 1 — А п ) ,

откуда после подстановки Q ( ^ , ^ ) в (13)-(16) она трансформируется в систему для W ( ^п ) :

(1   Ап)2 дW(^,п)   д2W(^,п) • п   дп      д^-

W ( ^ ,0 ) = 0;

W ( 0, п ) = 0 ;

W ( 1, п ) = 71 — А п exp

Далее введем вспомогательную функцию

—

V ( ^ , п ) = W ( ^ , п ) — U ( ^ , п ) , что позволяет представить (23) как

( 1 — А п ) 2

д V ( ^ , п )   д U ( ^ , п ) 1 _ д ² V ( ^ , п )   д ² Ц ( ^ , п )

дп

дп

д ^ 2

' -

,

а структура условий (24)–(26) определяет связь

U (^,п ) = ^W (1,п), поэтому из (24)-(26) и (28), (29) следует система для определения V(^,п)

( 1 — А п )

2 д V ( ^ , п )   д 2 V ( ^ , п )

^{— 1} ^ А ( 1 ^{— А} п ) 2

д п

—

V¹ — А п

д^"

^А 71 — А п exp

—

—

А ( 1 — А п ) ;

;

V ( ^ ,0 ) = — ^ exp ^— ^А J ;

V ( 0, п ) = 0;

V ( 1, п ) = 0.

К системе (30)–(33) применено интегральное синус-Фурье преобразование [10] по переменной £

ф( А ,п )=J V (£,п) sin (V) d- , где An = nn, n = 1,да, которое систему (30)-(33) переводит в задачу Коши:

d XXA +   ^ ф( A n , п ) = F ( , ) ;

d n      ( 1 - A n ) 2

Ф ( A n ,0 ) =

cos A n

a

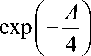
где х A cos A (     1      A г---—)   Г A,.   . х

F ⁽ П ) = - —- ^-      ■   4 ^{1 -} A n exP — ^{(1 -} A n )

^{2   A} n  ( V¹ - A n   ²         J L ⁴        .

Решение (34)–(35) есть

^ф ( ^A n , n ) = ^exP

A ( 1 - A n ) ²

A ( 1 - A n ) 2

d n " .

Оригинал (36)

да

V V^n ) = ² Е ^ф ( ^A n , n ) sin ( ^A n ^) .

n = 1

Из (12), (17), (26), (27), (37) следует окончательное решение задачи (6)–(10)

T ( X , e ) =

да

^{1   A e}             n = 1

x sin

A X . )1   1

1 - A e J J и A e

1 _л exp — A

X ²

которое корректно при e <  1/ A .

Анализ. Расчеты показывают, что при A = 0 (граница не движется) изменение профиля температуры (рис. 2) соответствует известным результатам [11]. В случае A >  0 (рис. 3) полученные результаты отражают физическую картину различных процессов [6], причем при изменении среднеинтегральной температуры в полосе наблюдается максимум, который с ростом A смещается к неподвижной границе (рис. 4).

В предположении, что толщина полосы является параметром, решение задачи в исходной формулировке с помощью метода одностороннего преобразования Лапласа по e [12] представле- на в виде:

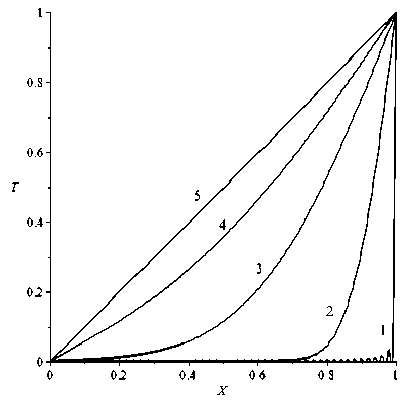
Рис. 2. Изменение локальной температуры по высоте полосы при A = 0 для различных e : 1–10^–5; 2 – 0,2; 3 – 0,4; 4 – 0,6; 5 – 0,8

т ( x ,e ) = -X-+-42- x v ’ h(e) h(e)

”   sin ( Ц п ^Х )           2

^x L              exp ( ^- ^ n ^e ) ;

n = 1 ^cos Г ^ n^H ( ^e ) J

H ( e ) = 1 - A e ; ц _п = n n] h ( e ) , n = 1, да , x <  h ( e ) .

Правомерность такого приема показана в [13].

Заключение . Сведение задачи переноса теплоты теплопроводностью в бесконечной полосе с перемещением по нормали одной из границ к другой с постоянной скоростью к задаче с неподвижными границами с помощью автомодельного преобразования координат позволяет получить ее точное аналитическое решение в квадратурах.

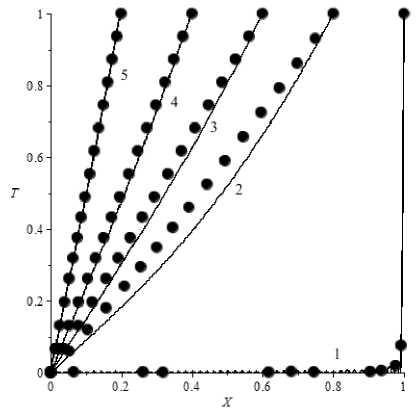
Рис. 3. Изменение профиля температуры по высоте полосы при A = 1 при различных 6 : 1 - 10^-5; 2 - 0,2; 3 -0,4; 4 – 0,6; 5 – 0,8

• – приближенное параметрическое решение

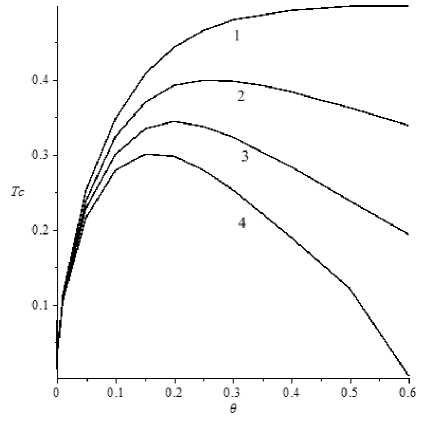
Рис. 4. Изменение среднеинтегральной температуры в полосе при различных A : 1 – 0; 2 – 0,5; 3 – 1,0; 4 – 1,5