Тепловое перепутывание в двойной модели Джейнса - Каммингса

В настоящее время перепутанность признана основной особенностью квантовой физики и рассматривается в качестве источника разнообразных применений в квантовой информации. В последние годы атомное перепутанное состояние интенсивно исследовалось в системах двух- и многоатомных естественных или искусственных атомов, таких как сверхпроводящие цепи, ридберговские атомы, ионы и т. д. [1–3]. Хорошо известно, что взаимодействия между атомами и окружающей средой обычно ухудшают степень их перепутывания. Однако в некоторых ситуациях, напротив, взаимодействие атомов со средой может генерировать атомную перепутанность [4]. В частности, взаимодействие атомов с тепловым полем резонатора может вызвать их перепутывание, как было показано Кимом и соавторами [5]. Ким и соавторы исследовали этот эффект для двух двухуровневых атомов, взаимодействующих с одномодовым тепловым полем через однофотонные переходы в резонаторе без потерь. Позже аналогичный эффект был предсказан и для многих других обобщенных двухатомных моделей Джейнса – Каммингса (МДК) с учетом вырожденного и невырожденного двухфотонного перехода, штарковского сдвига, расстройки, атомной когерентности, диполь-дипольного взаимодействия и т. д. [6–15]. Недавно Йонак и др. [16; 17] предложили так называемую двойную МДК, состоящую из двух двухуровневых атомов и двух резонаторных мод, при условии что каждый атом взаимодей- ствует только с одной модой индивидуального резонатора, и исследовали динамику атом-атомного перепутывания этой модели: они обнаружили, что для слабых малофотонных полей перепутанность кубитов не является стационарной и может демонстрировать периодические флуктуации в виде внезапной смерти и рождения перепутывания атомов. В последнее время двойная МДК широко исследовалась в большом количестве работ [18– 28]. В настоящей статье мы изучали динамику атом-атомного перепутывания в двойной МДК, в которой два идентичных двухуровневых атома резонансно взаимодействуют с тепловыми полями двух резонаторов.

1.    Модель и ее нестационарная динамика

Мы рассмотрели два одинаковых кубита – A и B – и две тепловые резонаторные моды копланарных резонаторов, или LC-цепей, обозначенных как «1» и «2», с одинаковыми частотами и средним числом тепловых фотонов (одинаковыми температурами резонаторов). Кубит A резонансно взаимодействует с одномодовым полем резонатора «1» , а кубит B резонансно взаимодействует с полем одномодового резонатора «2». Предположим также, что константы связи поля кубитов равны. Гамильтониан рассматриваемой системы в приближении картины взаимодействия и в приближении вращающейся волны можно записать в виде

H = Й g ( ^ A a + a + c _A ) + % Y ( c B b + b ⁺c _B ),               (1)

где ст + =| +) _и (- 1 и ст - =| - _и {+ | - операторы перехода между возбужденным | +) i и основным | - i состояниями в кубите ( i = A , B ); a ⁺ и a - операторы рождения и уничтожения фотонов (или плазмонов для LC-резонатора) моды резонатора «1»; b ⁺ и b - операторы рождения и уничтожения фотонов моды резонатора «2»; γ – константа связи между каждым из кубитов и полем резонатора.

Сначала рассмотрим два кубита в начальном перепутанном состоянии белловского типа:

| Ψ (0) 〉 _A = cos θ | + , -〉 + sin θ | - , +〉 ,                      (2)

а поля резонаторов изначально в тепловом состоянии с матрицей плотности

ρF(0)=∑pn1pn2|n1,n2〉〈n1n2|, n nn+1

где p n = n j j /(1 + n j ) j и n j - среднее число фотонов в моде резонатора j ( j =1,2); n j = (ехр[ й ю / k B T ] - 1] ^{- 1}; k_B - постоянная Больцмана; T – равновесная температура резонаторов. Тогда полная начальная матрица плотности для рассматриваемой модели есть

ρ (0) =| Ψ (0) 〉 _AA 〈Ψ (0) | ⊗ρ _F (0).

Мы намерены получить точную динамику рассматриваемой модели. Начнем наше исследование с ситуации, когда два атома взаимодействуют с резонаторными полями, подготовленными в фо-ковских состояниях, а затем обобщим полученные результаты на случай тепловых полей.

Для фоковских состояний поля решение уравнения Шредингера для рассматриваемой модели имеет вид

| Ψ ( t ) 〉 _{n 1, n 2}= X _{1, n 1, n 2}( t )| - , - ; n ₁ + 1, n ₂ 〉+ + X _{2, n 1, n 2}( t )| - , - ; n ₁, n ₂ + 1 〉+ + X _{3, n 1, n 2}( t )| + , - ; n ₁, n ₂ 〉+

+ X _{4, n 1, n 2}( t ) | + , - ; n ₁ - 1, n ₂ + 1 〉+                        (3)

+ X _{5, n 1, n 2}( t )| - , + ; n ₁ + 1, n ₂ - 1 〉+

+ X _{6, n 1, n 2}( t )| - , + ; n ₁, n ₂ 〉+

+ X _{7, n 1, n 2}( t )| + , + ; n ₁, n ₂ - 1 〉+ + X _{8, n 1, n 2}( t ) | + , + ; n ₁ - 1, n ₂ 〉 .

В случае n ₁ ≠ n ₂ - 1 или n ₂ ≠ n ₁ - 1 и n ₁ ≠ 0, n ₂ ≠ 0 коэффициенты в формуле (3) имеют вид

X _{1, n , n} ( t )]= - cos θ (( i 1 + n ₁(( n ₂ + (1 + n ₁) n ₂) ×

× Ω ₁ ^- ( n ₁, n ₂) sin[ Ω ₁ ⁺ ( n ₁, n ₂) γ t ] +

+Ω ₁ ⁺ ( n ₁, n ₂)( - n ₂ + (1 + n ₁) n ₂) sin[ Ω ₁ ^- ( n ₁, n ₂) γ t ])) /

/ (2 (1 + n ₁) n ₂ Ω ₁ ⁺ ( n ₁, n ₂) Ω ₁ ^- ( n - 1, n ₂))),

X _{2, n , n} ( t )] = - sin θ (( i 1 + n ₂(( n ₁ + (1 + n ₂) n ₁) ×

× Ω ₂ ^- ( n ₁, n ₂) sin[ Ω ₂ ⁺ ( n ₁, n ₂) γ t ] +

+Ω ₂ ⁺ ( n ₁, n ₂)( - n ₁ + (1 + n ₂) n ₁) sin[ Ω ₂ ^- ( n ₁, n ₂) γ t ])) /

/ (2 (1 + n ₂) n ₁ Ω ₁ ⁺ ( n ₁, n ₂) Ω ₁ ^- ( n - 1, n ₂))),

X _{3, n , n} ( t )]=(1/2)cos θ×

× (cos[ Ω ₁ ⁺ ( n ₁, n ₂) γ t ] + cos[ Ω ₁ ^- ( n ₁, n ₂) γ t ]), X _{4, n , n} ( t )] = (1/2) ( sin θ (cos[ Ω ₂ ⁺ ( n ₁, n ₂) γ t ] -

- cos[ Ω ₂ ^- ( n ₁, n ₂) γ t ] ) ,

X _{5, n , n} ( t )] = (1/2) cos θ (cos[ Ω ₁ ⁺ ( n ₁, n ₂) γ t ] -- cos[ Ω ₁ ^- ( n ₁, n ₂) γ t ]),

X _{6, n , n} ( t )] =(1/2)(sin θ (cos[ Ω ₂ ⁺ ( n ₁, n ₂) γ t ] + + cos[ Ω ₂ ^- ( n ₁, n ₂) γ t ]),

( t )] = - cos θ (( in ₂((1 + n ₁ + n ₁(1 + n ₂)) ×

X 7, n ₁, n ₂

× Ω ₁ ^- ( n ₁, n ₂) sin[ Ω ₁ ⁺ ( n ₁, n ₂) γ t ] +

+Ω ₁ ⁺ ( n ₁, n ₂)(1 + n ₁ + (1 + n ₁) n ₂) sin[ Ω ₁ ^- ( n ₁, n ₂) γ t ])) /

/ (2 (1 + n ₁) n ₂ Ω ₁ ^- ( n ₁, n ₂) Ω ₁ ⁺ ( n - 1, n ₂))),

X _{8, n , n} ( t )] = - sin θ (( in ₁((1 + n ₂ + (1 + n ₂) n ₁) × × i Ω ₂ ^- ( n ₁, n ₂) i sin[ Ω ₂ ⁺ ( n ₁, n ₂) γ t ] +

+Ω ₂ ⁺ ( n ₁, n ₂)( - 1 - n ₂ +- (1 + n ₂) n ₁) sin[ Ω ₂ ^- ( n ₁, n ₂) γ t ])) /

/ (2 (1+n2)n1Ω1-(n1,n2)Ω1+(n-1,n2))), где

Ω ₁ ⁺ ( n ₁, n ₂) = 2 (1 + n ₁) n ₂ + n ₁ + n ₂ + 1;

Ω ₁ ^- ( n ₁, n ₂) = 2 (1 + n ₁) n ₂ - n ₁ - n ₂ - 1;

Ω ₂ ⁺ ( n ₁, n ₂) = 2 (1 + n ₂) n ₁ + n ₁ + n ₂ + 1;

Ω ₂ ^- ( n ₁, n ₂) = 2 (1 + n ₂) n ₁ - n ₁ - n ₂ - 1.

Для случая n ₁ =0 или n ₂ =0 коэффициенты в (3) принимают вид

X _{1,0, n} ( t ) = - i cos θ cos( n ₂ γ t )sin( γ t ),

X _{2,0, n} ( t ) = - i sin θ sin( 1 + n ₂ γ t ),

X 3 0 n ₂ ( t ) = cos 9 cos( Y t ) cos( 7 ^ 2 Y t ),

X 4 0 n ₂( t )=0

X 5 0 n ₂ ( t ) = - cos 9 sin( t ) sin(^ П ^ Y t ), X 6, ₀ , n ₂ ( t ) = sin 9 cos(^1 + n ₂ Y t ), X 7 o _n ( t ) = - i cos 9 cos( t )sin(7 ^ 2 y t ),

X     ( t )=0;

n ₂

sin 9 i V1 + n

^X 8, n , n ⁽ t ) ^{- Y} 8, n ⁽ t ) =        1 ^x

^{1 2}             2V2V n ² — 1

x ^[ i to — (( to + )² — 1) i sin(^ to + Y t ) + nn       n

+ito + (1 — (to n )2) i sin( V2 to nY t )"|, где to"

— 1.

Наконец, для случая n 1 = n — 1, n 2 = n ( n >1) получаем:

X _{1 n} ,o( t ) = - i cos 9 sin(^1 + "  1 Y t ),

X 3, _{n i} ,₀( t ) = cos 9 cos(71 + n 1 Y t ),

X 4, _{n i} ,0 ( t ) = — sin 9 sin( Y t ) sin( ^ n ^ 1 y t ),

X 5, n ₁,0( t )=0,

X 6, _n ,₀( t ) = sin 9 cos( y t )cos(7 " "Y t ),

X 7, n ₁,0( t )=0,

X 8 _n 0( t ) = — i sin 9 cos( Y t )sin(Т " "Y t ).

Для случая n 1 = n — 1, n 2 = n ( n > 1) соответственно имеем:

X 1, _{n i}, о , ( t ) - Y 1, _n ( t ) = — 2 cos 9 sin(2 V n y t ),

X2n n (t) - Y2 Vt) =sn

2,n1,n2

2V2V n — 1

xi[ V n — 1 to— (1 + (to+ )2 )i sin(V2to+Y t) —, nnn

^X 1, n , n ₂ ( t ) - Z 1, n ( t ) = cos7=

x[ i to— ((to+ )2 — 1) i sin(V2to+Y t) + nnn

+i to+ (1 — (to— )2) i sin(V2to—Y t)], nnn

— 1

—

■ to + (1 + ( to_n )² ) sin i (^ to_nY t ) ] , nn    n

X ₃n n ( t ) - Y ₃ n( t ) = 1 cos 9 ^[ 1 о , n 1 , i n 2            , n 2 J

X.„ „ ( t ) - Y ,„( t ) = sn ^ S 4, n ₁, n ₂        4, n ₂

— 1

2\ n — x ( cos(V2 to + Y t ) — cos(V2 to _nY t ) ] ,

X_5n n ( t ) - Y 5 V t ) = 1 cos 9 ^[ - 1 + cos' , ⁿ 1 , in 2             ^{, n}        2          1

X 6, n ₁, n ₂

= — sin 9

( t ) - Y 6nn ( t ) =

[ cos(V2 to + Y t ) + cos(V2 to _nY t ) ] ,

X_7n n ( t ) - Y y V t ) = — ¹ cos 9 i sin(2V " Y t ), n ₁ n ₂         n ₂

X 2, n ₁, n ₂ (

X 3, n ₁, n ₂(

= —cos 9

( t ) - ^ 2 _n ( t ) = —^sin 9 i sin(2T n Y t ), ( t ) - Z 3, _n ( t ) =

[ cos(V2 to + y t ) + cos(V2 to _n Y t ) | ,

X4n n (t) - Z4 n(t) = 1 sin9[ 4,n1,n2

cos 9

X5 n П (t) - Z5 n(t) =/

5,n1,n2

x V n ² — 1 (cos(V2 to + 1 )

—

= x

cos(V2 to _n Y t ) | ,

^X 6, n 1 , n 2 ⁽ t ) ^{- Z} 6, n ⁽ t ) = ¹ sin ^{9[— 1 +} cos

X ₇n n ( t ) - Z y n( t ) =--- cos-⁹— x

⁷ , ⁿ 1 , ^{n 2}       7, ⁿ     2V2 V n ²^^

x i ^[ V n — 1 to — (1 + ( to ⁺ )² 7 sin(V2 to ⁺ Y t )■ nn    n

—

—

■ to + (1 + ( to _n )²) sin i (^ to _nY t ) | ,

X 8, _{n i}, n ( t ) - Z ₈ , _n ( t ) = — 2 sin 9 sin(2V n Y t ).

Используя зависящую от времени волновую функцию для начальных фоковских состояний полей резонатора, можно легко получить зависящую от времени матрицу плотности для тепловых полей: p ⁽ t ) = E P n₃ P n₉ I ^{V (} t ) > n , n₉n₃ , n ₂<^{V (} t ) I.               ⁽⁴⁾

1 2      1 212

n ₁, n ₂

Взяв частичный след по переменной поля для полной матрицы плотности (4), мы можем получить приведенную атомную матрицу плотности p ( t ) a = Tr F p ( t ) и вычислить параметр перепутанности между кубитами.

2.    Перепутывание между двумя кубитами

Для системы двух кубитов, описываемых оператором р a ( t ), мера перепутывания или отрицательность может быть определена в терминах отрицательных собственных значений ц - частичного транспонированная по переменным одного кубита атомная матрица плотности ( р A ).

s = - 2 ^ ц - , (5) где s = 0 означает, что два кубита находятся в сепарабельном состоянии, и s > 0 - появление перепутывания между ними. Случай s = 1 соответствует максимальной степени перепутывания кубитов.

Редуцированная матрица атомной плотности для рассматриваемой системы есть

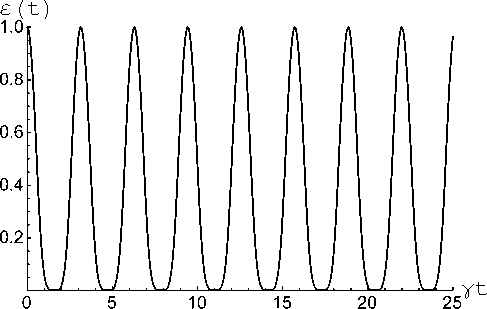
Рис. 1. Отрицательность как функция безразмерного времени у t для начального перепутанного атомного состояния (2). Среднее число фотонов для резонаторов n 1 = n ₂ = 0. Параметр 0 = п / 4

Fig. 1. Negativity as a function of the dimensionless of time у t for the initial entangled atomic state (2). Average number of photons for resonators n 1 = n ₂ = 0. Parameter 0 = п / 4

	Г и	0	0	H ^
	0	V	H	0
Р A ( t ) =	0	H	W	0	.                                              (6)
	0 V	0	0	R V

Формулы для матричных элементов U , V , W , R и H в настоящей работе не приведены, т. к. они имеют слишком громоздкий вид. Частично транспонированная по переменным одного кубита матрица плотности для (6) есть

	и	0	0	H
T P A 4 t ) =	0	V	0	0	.                                            (7)
	0	0	W	0
	H V	0	0	R V

Матрица (7) имеет только одно собственное значение, которое может принимать отрицательные значения, поэтому в рассматриваемом случае отрицательность можно записать как

s ( t ) = 7( R - и )² + 4 H ² - и - R. (8)

3.    Результаты и обсуждение

Отрицательность (8) для перепутанного начального атомного состояния (2) как функция безразмерного времени у t изображена на рис. 1 для вакуумных начальных состояний резонаторов. На рис. 2 представлена временная зависимость отрицательности для начального состояния кубитов (2) и тепловыми резонаторами с различными значениями средних чисел фотонов n ₁= n ₂= 0.5 (сплошная линия), n ₁= n ₂=1 (штриховая линия) и n ₁= n ₂=2 (точечная линия). Кривые на рис. 1 и 2 были получены в предположении, что 0 = п /4.

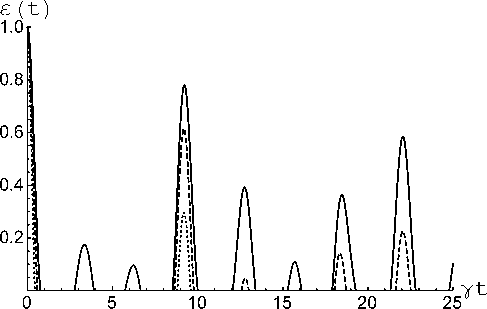
Рис. 2. Отрицательность как функция безразмерного времени y t для начального перепутанного атомного состояния (2). Среднее число фотонов для тепловых резонаторов n 1 = n 2 = 0,5 (сплошная линия) n 1 = n 2 = 1 (пунктирная линия) и n 1 = n 2 = 2 (точечная линия). Параметр 0 = п / 4

Fig. 2. Negativity as a function of dimensionless of time Y t for the initial entangled atomic state (2). Average number of photons for thermal resonators, n 1 = n ₂ = 0,5 (solid line) n 1 = n ₂ = 1 (dotted line) and n 1 = n ₂ = 2 (dotted line). Parameter 0 = п / 4

Из рис. 1 видно, что для вакуумных состояний полей резонаторов отрицательность имеет очевидную периодичность и начальная максимальная степень перепутывания кубитов восстанавливается в моменты времени yt = пк, где к = 1,2 ... Взаимодействие кубитов с тепловыми полями разрушает исходные квантовые корреляции атомов, однако для определенных моментов времени происходит частичное восстановление перепутывания кубитов даже при относительно высоких температурах резонатора (n1, n2 < 2). В этом случае периодичность эволюции параметра перепутанности нарушается. Из рис. 2 также хорошо видно, что для теплового поля резонатора имеет место внезапная смерть и рождение перепутывания кубитов.

Заключение

Мы исследовали динамику перепутывания двух изначально перепутанных двухуровневых атомов (кубитов), взаимодействующих с двумя независимыми модами тепловых резонаторов в рамках двойной модели Джейнса – Каммингса. Нами найдено точное решение для рассматриваемой модели, и на его основе получено аналитическое выражение для параметра перепутывания атомов ‒ отрицательности. Результаты численного моделирования временной зависимости отрицательности показали, что начальная атомная перепутанность может частично восстановить свое первоначальное значение в процессе эволюции рассматриваемой системы даже при относительно высоких температурах резонатора. Таким образом, взаимодействие атомов с тепловыми фотонами, которые всегда присутствуют в резонаторах конечной температуры, не приводит к полному исчезновению начальных наведенных локальных квантовых корреляций состояний атомов.