Тепловой расчет конструкций

УДК 697.1                                                    

Введение. Тепловые расчеты при производстве строительных конструкций ветроэнергетических установок в настоящее время приобретают большое значение. По планам Министерства энергетики РФ 1 в стране в ближайшие годы будет создана индустрия ветровой энергетики. В 2016–2017 гг. в нее пришли крупные российские и иностранные инвесторы, которые взяли обязательства по развитию технологической и производственной базы. Устраняются основные недостатки лопастных ветроэнергетических установок путём совершенствования их конструкции и технологии изготовления. В первую очередь это относится к лопастям, которые являются основными элементами ветротурбины, концентрирующими главную интеллектуальную составляющую установки. Производство стеклопластиковой лопасти представляет собой сложный термохимический процесс, включающий полимеризацию связующего при строго заданном тепловом режиме. В связи с этим точный расчет температурных полей в теле лопасти при ее формовании имеет большое практическое значение.

Определение полей температур конструкции сложной формы, выполненной из неоднородных материалов, приводит к необходимости применения в расчетах численных методов и, в первую очередь, метода конечных элементов (МКЭ). Проблема конечно-элементного моделирования композиционных материалов при формовании остается до настоящего времени нерешенной. Это определяется сложностью поведения композита как неоднородного материала, обладающего ярко выраженными термозависимыми физическими, в т. ч. реологическими свойствами, остаточными внутренними явлениями, старением и др.

Машиностроение и машиноведение

Современные модели учитывают анизотропность материала, его пластическое поведение при сложном напряженно-деформированном состоянии и др. Так, в работах [1, 2] исследованы температурные свойства композиционных материалов. Для обоснования и подтверждения влияния распределения и ориентации упрочняющих частиц на коэффициент температурного расширения материала авторами выполнено конечно-элементное моделирование. При геометрическом построении за основу была принята реальная микроструктура. Расчетами установлено, что экспериментально обнаруженная анизотропия температурных свойств объясняется внутренними напряжениями в композите, зависящими от ориентации наполнителя.

Многие исследования посвящены расчетам двумерных моделей армированных композиционных материалов. Для анализа и оптимизации свойств композита предложена расчётная конечно-элементная схема, учитывающая его температурные свойства [3]. С помощью МКЭ рассчитаны поля остаточных напряжений, образующихся в матрице в результате термической обработки для модели композита, включающего армирующие волокна [4]. С использованием конечно-элементной модели рассчитаны эффективные упругие характеристики многослойного композиционного материала, причем каждый слой описывался собственными термомеханиче-

1Возобновляемая энергетика в России состоялась как отрасль / Министерство энергетики российской федерации // : [сайт]. URL: (дата обращения: 04.02.2021).

скими свойствами [5]. Моделирование поведения анизотропных материалов и другие вопросы термонагружения проанализированы также в работах [6–13].

Большинство исследований, базирующихся на конечно-элементном анализе, выполнены с использованием универсальной программной системы ANSYS, позволяющей решать линейные и нелинейные, стационарные и нестационарные пространственные задачи теплопередачи и теплообмена. Например, с помощью ANSYS решены задачи:

• •    нестационарного нагрева конструкции при наличии зависимости от времени коэффициента конвекции²;.

• •    теплового расширения элементов при интенсивном нагреве³;

• •    тепловыделения при пластической деформации⁴;

• •    передачи теплоты в многослойных конструкциях через границу раздела сред⁵ и др.

Исследованию процессов обработки полимерных композиционных материалов посвящены работы С. Н. Шевцова, например [14]. Несмотря на большое количество работ, посвященных численным тепловым расчетам, актуальность оценки теплового режима формования конструкций лопастных установок сохраняется. Повышение требований к качеству производства элементов ветротурбин приводит к необходимости дальнейшего уточнения математических конечно-элементных моделей теплопередачи на основе более полного учета внешних и внутренних факторов.

Целью работы является исследование нестационарных полей температур составной конструкции сложной объемной формы лопастного элемента ветроэнергетической установки в процессе ее изготовления при учете физических особенностей и геометрических нелинейностей. Одна из конструкций состоит из лонжерона и хвостового отсека, части которых выполнены из стеклопластика, резины, вспененного пластика и др. Хвостовой отсек изготавливается по клеевой технологии в специальном приспособлении, которое состоит из верхнего и нижнего полукорпусов с мощными ребрами жесткости. Между ними закладывается лопастной элемент. Для его качественной склейки необходимо строго выдерживать скорость нагрева и температуру выдержки в клеевых швах. Задание теплового режима осуществляется размещением приспособления с отсеком в нагревательной печи.

Постановка задач работы состоит в следующем. Требуется создать конечно-элементную модель нагрева лопастного элемента при его формовании, рассчитать объемные поля температуры в любой момент процесса, определить точность моделирования тепловых процессов в теле конструкции, а также сформировать график набора температуры в печи, обеспечивающий требуемый режим нагрева клеевых зон отсека.

Материалы и методы. Основой тепловых расчетов является утверждение первого закона термодинамики о том, что количество теплоты, полученное изолированной системой, затрачивается на изменение ее внутренней энергии. Применительно к элементарному объему это утверждение можно выразить математически:

р с( д T / д t + { V } T { L } T) + { L } T { q } = q v ,                                    (1)

где ρ — плотность материала; с — удельная теплоемкость; T — температура; t — время; { q } — вектор теплового потока; q v — тепловыделение единичного объема.

Векторный оператор { L } и вектор скорости { V } для теплопередачи, реализуемой массой:

д дx д ду д

{ LM

{ V M V г

V z jZz где x, y, z — координаты.

По закону Фурье тепловой поток связан с градиентом температуры:

{ q}=-[ D ]{ L} T,                                               (2)

где [ D ] — матрица теплопроводности:

[ D ] =

X x

X

y

X z

Объединяя (1) и (2), получим:

c( ST / 81 + {V }T {L} T) = {L}T ([D] {L} T) + ^v.(3)

Раскрывая (3), получим:

z5T тл 5T  тл 5T    8T .      d („ dT)  5 L  5T)  5 f, pc(+ V + V + V ) = q + IX 1 + IX 1 + IX I.

51   ”8x   y dy     5z     v  8x V ” 8x )  dy ( y dy )  dz ( 18z

Основное уравнение теплопроводности дополняется граничными условиями:

• 1.    Задание температуры на поверхности: T = T *.

• 2.    Задание теплового потока на поверхности:

• 3.    Теплопередача соответствует закону Ньютона (поверхностная конвекция):

{q }T {n} = - q*, где {n} — нормальный к поверхности единичный вектор; q* — удельный тепловой поток.

{ q}T { n} = af (Ts - Tb) , где αf — коэффициент теплопередачи, Ts — температура на поверхности, Tb — температура граничащей среды.

Для случая постоянных теплофизических коэффициентов исследуемые тепловые процессы описываются трехмерным уравнением нестационарной теплопроводности (уравнением Фурье):

8 T  „ f 5 2 T d¹ T  d¹ T )

• p c    =X +    +      ,

5 1     V^е x 2    d y ¹    8 z ¹ )

где λ — коэффициент теплопроводности.

В связи с симметричностью задачи расчет проводится лишь для половины конструкции. Граничные условия для плоскости сечения определяются из условия: q = 0.

На стыковочных поверхностях предполагается идеальный тепловой контакт, отсутствие термического сопротивления:

T - о = T | + 0 ; X i d T l- о =X i d T |+ 0 .

6 x        d x

Конвективные тепловые потоки подводятся к наружным поверхностям приспособления. Внутреннее тепловыделение при нагреве не учитывается . Начальные условия предполагают фиксацию постоянной температуры по всей исследуемой области: T = T 0 .

Задача решена методом конечных элементов в многофункциональном программном комплексе ANSYS на языке параметрического программирования APDL. Конструкция нагревается с наружной поверхности конвекцией. Результаты разбивки приспособления и отсека на блоки, а также на объемные тетрагональные конечные элементы представлены на рис. 1.

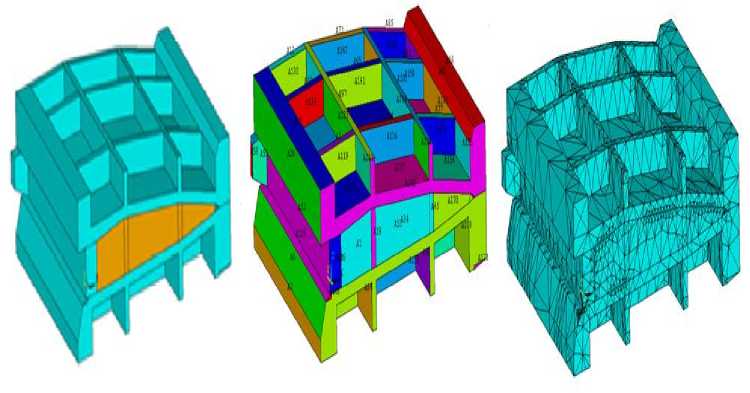
а )                            б )                                     в )

Рис. 1. Склеечное приспособление с хвостовым отсеком: а — общий вид; б — поверхности модели с указанием их номеров; в — разбивка анализируемой области на конечные элементы

Машиностроение и машиноведение

Теплофизические свойства материалов, используемых в расчетах, приведены в таблице 1.

Таблица 1

Материал	λ, Вт/(м∙К)	c , Дж/(кг∙К)	ρ, кг/м 3
Стеклопластик	0,38	1230	1710
Al-сплав	176	798	2700

Теплофизические свойства материалов

Созданная для решения поставленной задачи программа определяет значения температуры в каждом расчетном узле на протяжении всего технологического процесса склейки.

Алгоритм расчета состоит из следующих шагов:

• •    задание исходных данных (геометрии, теплофизических свойств, начальной температуры и т. п.);

• •    разбивка области на конечные элементы;

• •    приложение тепловых источников;

• •    определение температуры области в конце шагов нагрева;

• •    вывод результатов расчета (тепловых потоков, температурных полей) на печать.

Для проверки правильности работы программа проходила тестирование. На рис. 2 показаны экспериментальные и расчетные зависимости температуры от времени в клеевой зоне (нижние кривые) и в самой печи (верхние кривые). Абсолютная погрешность расчета температуры в точке склейки не превышает 5 оС, относительная погрешность для реально значимых температур — не более 6 %.

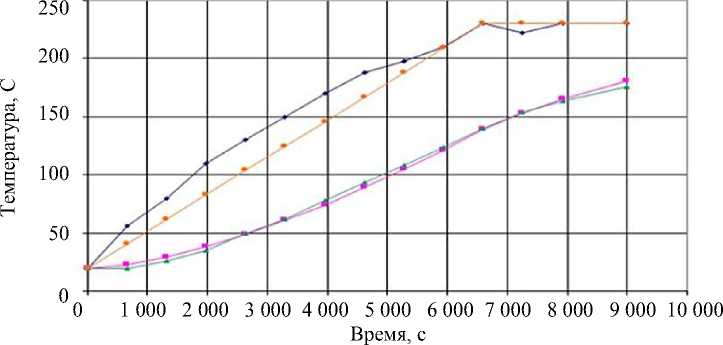
Реальная задающая Т          Расчетная контрольная Т

Реальная контрольная Т        Расчетная задающая Т

Рис. 2. Зависимости от времени расчетных и измеренных температур в контрольной и задающей точках

Результаты исследования. Технологический процесс включает в себя монотонный, непрерывный нагрев склеечного приспособления и лопастного элемента до определенной температуры и ее поддержание заданное время. Результаты расчета приведены на рис. 3–7. Так, на рис. 3 представлено распределение по объему в определенный момент времени тепловых потоков в векторной форме и суммарное количество теплоты в теле приспособления с отсеком.

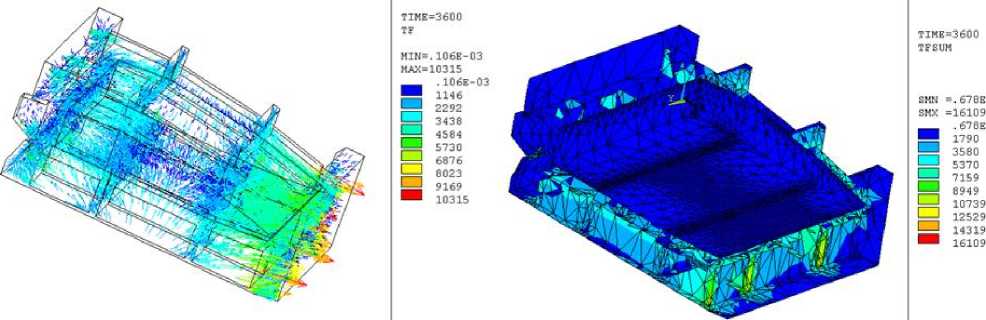
а )                                                              б )

Рис. 3. Тепловые потоки ( а ) и суммарный нагрев ( б ) приспособления с отсеком

Так как скорость нагрева приспособления относительно невелика, тепловые потоки перераспределяются по его объему равномерно и оказываются приблизительно одинаковыми по всем направлениям. Небольшие исключения касаются лишь ребер жесткости. Конвективные тепловые потоки подводятся с боков, имеющих большую площадь, а отводятся теплопроводностью в тело полукорпусов через узкое поперечное сечение.

На рис. 4 представлены температурные градиенты в теле приспособления с отсеком в один из моментов нагрева. Видно, что тепло распространяется от наружных поверхностей приспособления к внутренним областям. Тепловые потоки наиболее активно подводятся в местах близких к боковому вкладышу и перемещаются одновременно как от бокового вкладыша, так и от верхнего и нижнего полукорпусов приспособления. На этом же рисунке представлен объемный вид температурного поля в аналогичный момент времени. Поскольку лопастной отсек неметаллический, его теплопроводность низка, и распределение температуры оказывается не- равномерным.

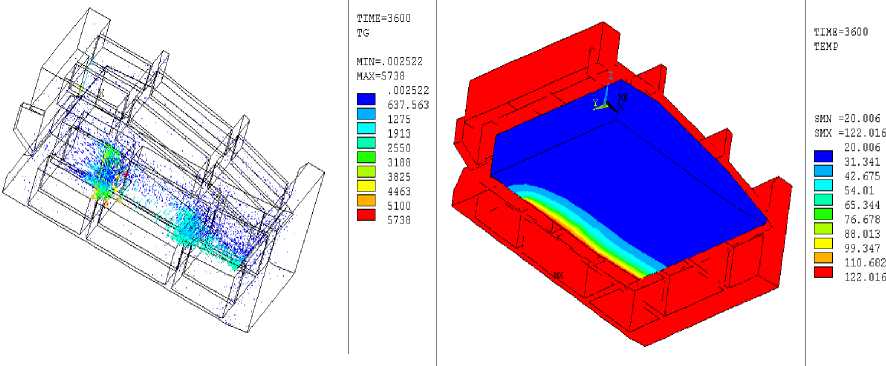
а )                                                        б )

Рис. 4. Векторные поля градиента температуры ( а ) и температуры ( б ) в теле приспособления с лопастным отсеком

Зависимости температуры от времени в отдельных точках клеевой зоны представлены на рис. 5-7. Изменением значений задающих температур окружающей среды и количества их переключений можно добиться максимального соответствия графика набора и выдержки температуры в клеевых зонах требованиям техноло-

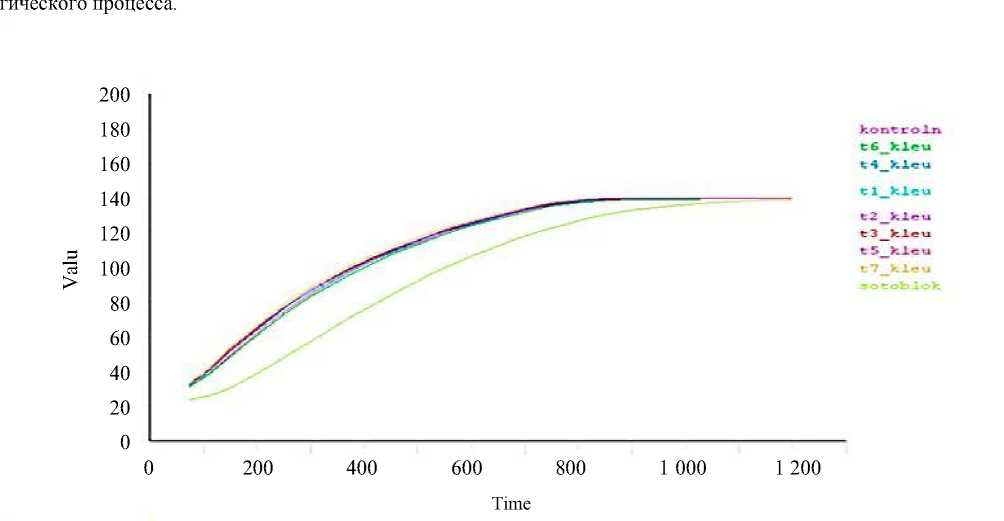
Рис. 5. Зависимости температуры от времени в характерных точках клеевых зон и в блоке (зеленая линия) для технологического режима, включающего два переключения при задающих температурах 160 и 140 °С

Машиностроение и машиноведение

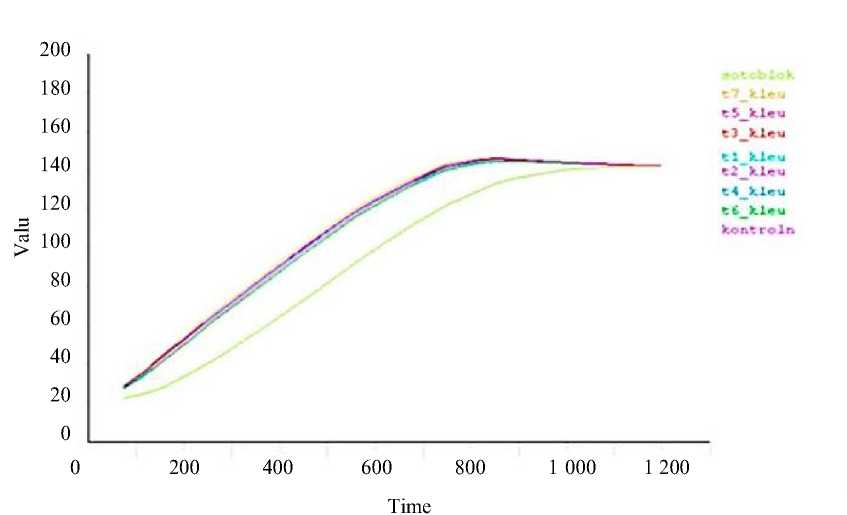
Рис. 6. Зависимости температуры от времени в характерных точках клеевых зон и в блоке (зеленая линия) для технологического режима, включающего четыре переключения при точности задания температуры до 10 °С

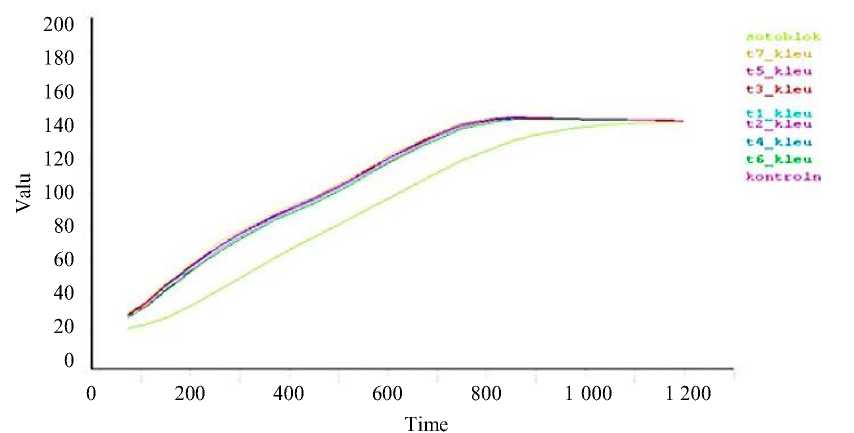
Рис. 7. Зависимости температуры от времени в характерных точках клеевых зон и в блоке (зеленая линия) для технологического режима, включающего три переключения

Обсуждение и заключения. Выполненный тепловой расчет элементов строительных конструкций ветроэнергетических установок на этапе изготовления позволил выявить характерные особенности нагрева и получить рекомендации по уточнению параметров технологического процесса их склейки.