Тепловые свойства, магнето- и барокалорический эффекты в кристалле La 07Pb 03MnO 3

^ ^ mce = L I I    ^dH ;       (1)

V ° T 7 p, H

A T MCE = [H ^{(d M} )    dH .       (2)

AD       C p , н ^Jo Vd T 7 р,н

Прямые измерения интенсивного МКЭ проводились очень редко [5; 6], хотя известно, что наиболее правильным и надежным способом определения реальных значений интенсивного теплового эффекта является проведение прямых измерений ΔT AD с помощью адиабатического калориметра. Недавно нами были успешно выполнены такие исследования на некоторых сегнетоэлектриках [7; 8] и довольно сложных твердых растворах (La 1-y Eu y ) 0,7 Pb 0,3 MnO 3 (y: 0,2; 0,6) [9; 10].

Особый интерес представляет изучение различных калорических эффектов и повышение эффективности материала путем одновременного использования различных внешних полей. Лишь несколько работ посвящено одновременному изучению барокалорического эффекта (БКЭ) и МКЭ в одном и том же магнитном материале, в частности Ni-Mn-In, испытывающем ферромагнитный фазовый переход в узком диапазоне температур [11; 12].

Несмотря на то, что многие из твердых растворов были созданы на основе La 0,7 Me 0,3 MnO 3 (Me: Pb, Ca, Sr), информации об их теплофизических свойствах недостаточно. По данным рентгеновского исследования, при комнатной температуре [13], La 0,7 Pb 0,3 MnO 3

(LPM) характеризуется ромбоэдрической симметрией (пр. гр. R-3c). Фазовый переход между парамагнитной и ферромагнитной фазой был обнаружен при T 0 = 353 К. Ранее, ∆ S МКЭ и ∆ T ^МКЭ в La 1–-x Pb x MnO 3 (х: 0,1, 0,2, 0,3) были оценены на порошковых образцах [5].

В работе выполнены калориметрические, дилатометрические исследования и дифференциально термический анализ (ДТА) под давлением на монокристаллических образцах LPM. На основании анализа экспериментальных данных об энтропии и фазовой диаграмме был определен БКЭ и сопоставлен с МКЭ.

Исследования теплоемкости кристаллов LPM в широком диапазоне температур от 2 до 800 К проводились двумя калориметрическими методами. Низкотемпературные исследования в области между 2 и 370 К были выполнены на PPMS. В области от 370 до 800 К теплоемкость измерялась на дифференциальном сканирующем калориметре.

Для изучения интенсивного МКЭ мы провели прямые измерения температуры при изменении магнитного поля, используя адиабатический калориметр [9]. Образец LPM, состоящий из нескольких кусочков монокристаллов, с общей массой 1,05 г, был помещен в нагреватель, который состоит из полированного алюминиевого контейнера с константановым проводом, помещенным на его внутренней поверхности. Платиновый термометр сопротивления позволял с высокой точностью отслеживать температуру системы образец-нагреватель. Разница температур между термометром и образцом контролировалась двойной медь-константановой термопарой.

Измерения интенсивного МКЭ были проведены в соответствии со следующей процедурой: сначала образец охлаждался (или нагревался) до некоторой начальной температуры. Чтобы добиться оптимального значения | dT / dt | ≤ 3×10^-3 К/мин регулировалась температура образца. Включение магнитного поля H ведет к резкому росту температуры системы обра-зец+нагреватель ∆ T ^ON EXP . Затем достигается такая же температура, какая была до включения поля. Отключение магнитного поля сопровождается уменьшением температуры ∆ T ^OFF EXP до ∆ T ^ON EXP .

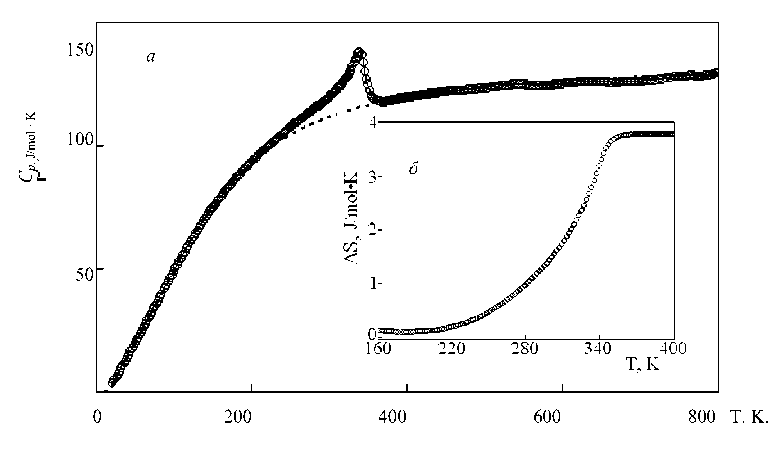
Рис. 1. Влияние гидростатического давления на фазовый переход LPM:

а – теплоемкость LPM как функция от температуры (штриховой линией показан решеточный вклад); б – поведение энтропии фазового перехода

Температура в системе образец+нагреватель ∆ T _EXP, полученная в экспериментах с магнитным полем, оказалось меньше, чем величина настоящего интенсивного МКЭ (∆ T ^МКЭ AD ). Причина в том, что изменение энергии образца, связанное с МКЭ, под воздействием магнитного поля в адиабатических условиях приводит к увеличению (или уменьшению) температуры как образца, так и нагревателя. Используя данные теплоемкости нагревателя Ch(T), можно определить теплоемкость образца C S (T). Оба значения C h (T) и CS(T), а также ∆ T EXP и ∆ T ^МКЭ AD связанны следующим соотношением [9; 10]:

( ^

MCE C h

А7 AD =А7EXP 11 +r I, (3) к CS которое позволяет нам получить информацию о действительном изменении температуры LPM при адиабатическом включении и выключении магнитного поля.

Измерения теплового расширения были проведены в температурном интервале 100–900 K, при помощи дилатометра NETZSCH DIL-402 C. Керамический образец в форме цилиндра (4 мм в диаметре и 5,17 мм в длину) был приготовлен из измельченных монокристаллов.

Влияние гидростатического давления на фазовый переход в LPM изучали на таком же образце, который ранее использовали для калориметрических исследований. Определяли температуру, связанную с аномалией теплоемкости, применяя дифференциальный термический анализ (ДТА). Монокристальный образец массой 0,234 г помещался в маленький медный контейнер, к которому приклеивался один из спаев медь-германиевой термопары. Второй спай приклеивался к кварцевому образцу, используемому в качест- ве эталонного вещества. Система помещалась во внутрь сосуда типа «пистон и цилиндр», соединенный с мультипликатором. Давление до 0,35 ГПа создавалось с помощью силиконового масла, употребляемого в качестве среды, передающей давление. Чтобы обеспечить достоверность результатов, измерения производились в циклах повышения и снижения давления (рис. 1).

Пик теплоемкости C p ( T ), обнаруженный при T 0 = 338,8 ± 0,5 K, согласуется с парамагнитным-ферромагнитным фазовым переходом (рис. 1, а ).

Суммарная энтропия, связанная с ферромагнитным фазовым переходом, определена по выражению S ₀ = ∫(Δ Cp ( T ) / T ) dT = 3,7 ± 0,3 Дж/моль·K. Ее температурная зависимость показана на рис. 1, б .

Соотношение между ∆ T ^МКЭ AD и ∆ T EXP , описанное при помощи формулы (3), сохранялось при 2,1 для всех изученных полей (рис. 2). При изменениях магнитного поля от 1,1 до 5,4 kOe, во всех случаях максимальное значение ∆ T ^МКЭ AD было получено при T MAX ≈ 342 K (рис. 2, а ). Соотношение (2) для интенсивного МКЭ показывает, что полученное несогласие может быть объяснено различными экстремумами функций C_{p ,H}( T ) и (∂ M /∂ T )_{p, H} [1]. Как было отмечено выше, измерения зависимости ∆ T ^EXP_AD ( H ) сопровождались сравнительно небольшим температурным дрифтом. Действительно, изменение температуры образца было меньше 0,07 К за 80 мин. Следовательно, можно рассматривать зависимости ∆ T ^МКЭ AD ( H ) как изотермы (рис. 2, б ). Никаких доказательств насыщения величины ∆ T ^МКЭ AD от поля, по крайней мере в области изученных полей, нет.

БКЭ – наиболее частая эффективная характеристика всех термодинамических систем, включая твердые тела. Он определяется как адиабатное изменение температуры ∆TBCEAD или изотермическое изменение энтропии ∆SBCE при увеличении и уменьшении давления:

^bce =-J p (I V ]   dp ;           (6)

0 V° T v p , H

BCE

^ T AD

T    p(a V)   ,

dp

г* и Jo ЙТ

C p , H <^d T v pH

Согласно формулам (6) и (7) оба значения зависят от теплового расширения материала и могут быть прямыми (∆ S БКЭ < 0, ∆ T ^БКЭ AD > 0) или обратными (∆ S БКЭ > 0, ∆ T ^БКЭ AD < 0) при dp > 0 в соответствии с положительным или отрицательным изменением объема вблизи точки фазового перехода.

Фазовая диаграмма давления-температуры для LPM была построена по результатам экспериментов в ДТА под давлением, которые обнаруживали аномалии теплоемкости, связанные фазовым переходом. Граница между парамагнитной и ферромагнитной фазазами описывается барическимо коэффициентом:

dT 0 / dp = 1,75 ± 0,25 K/кбар.

Принимая во внимание зависимости Cp(T) и T0(p), мы проанализировали БКЭ в LPM, используя подход, полученный в [14; 15], и успешно примененный для ферроэлектрических фазовых переходов второго рода [7; 8].

Основная идея этого метода в том, что на графике полной энтропии от температуры S ( T ) аномальная энтропия ∆ S смещается вдоль решеточной энтропии S L с увеличением давления, на величину барического коэффициента dT 0 / dp . Различие между температурами ∆ T ^БКЭ AD = T p ≠0 - T p =0 и энтропиями ∆ S БКЭ = S p ≠0 - S p =0 под давлением и при p = 0, а также постоянной энтропии и давлении – это и есть, соответственно, интенсивный и экстенсивный БКЭ. Температурная зависимость ∆ T ^БКЭ_AD для LPM представлена на рис. 3, a .

Зависимость ∆ T ^БКЭ AD под давлением T = const оказалась линейной (рис. 3, б ). Так же, как и в случае ∆ T ^МКЭ AD (рис. 2, б ) интенсивный БКЭ не доходит до насыщения при увеличении внешнего давления, по крайней мере в области исследованных давлений.

Таким образом, кристаллы La 0,7 Pb 0,3 MnO 3 , а также интенсивные МКЭ исследовали калориметрическими, дилатометрическими и ДТА-методами под давлением. Получена информация об энтропии фазового перехода и построена фазовая диаграмма темературы-давления. Интенсивные магнетокалорический и барокалорический эффекты линейно возрастают при увеличении магнитного поля и давления. LPM можно использовать как эффективный твердотельный хладагент в установках смешанного цикла на основе МКЭ и БКЭ.

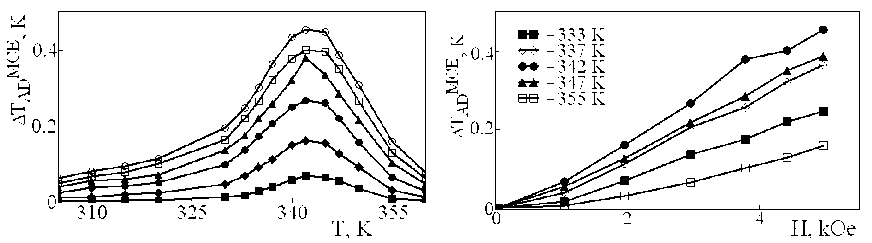
Рис. 2. Температурная зависимость интенсивного МКЭ:

а – для постоянных полей; б – максимальные значения Δ T ad ^МКЭ как функция поля для различных температур

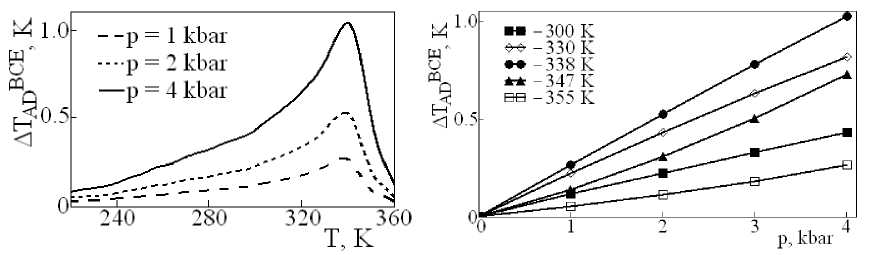
Рис. 3. Температурная зависимость интенсивного БКЭ:

а – для постоянных полей; б – максимальные значения Δ T ^БКЭ AD как функция давления для различных температур